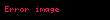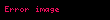Seyyar satıcı problemi yöneylem araştırması ve teorik bilgisayar bilimi alanlarında incelenen bir "kombinatorik optimizasyon" problemidir.
Tanımlama
Seyyar satıcı problemi şu şekilde tanımlanabilir:
- Bir seyyar satıcı var;
- Bu satıcı, mallarını
şehirde satmak istiyor;
- Öte yandan, mantıklı bir şekilde, bu satıcı bu şehirleri mümkün olan en kısa şekilde ve her bir şehre maksimum bir kere uğrayarak turlamak istiyor.
Problemin amacı, satıcıya bu en kısa yolu sunabilmektir.
Bu problem, bir matematiksel problem olarak 1930'lu yıllarda formüle edilmiştir. Optimizasyon konusunda en derin inceleme konularından biridir. "Hesaplamanın karmaşıklığı" teorisine göre çözümü NP-Tam olan en önemli algoritma problemlerinden biridir. Bundan dolayı seyyar satıcı problemlerini etkin olarak çözebilecek bir algoritma olmadığı kabul edilmektedir. Diğer bir deyimle en kötü durumda algoritma kullanılırken yapılan hesapların sayısının (yani bilgisayar kullanma zamanının) şehir sayıları arttıkça üstel olarak artması çok olasıdır. Bazı durumlarda sadece yüz şehirlik liste olmasına rağmen çözüm yapılırken çözümün yıllar alabileceği iddia edilmektedir.
Diğer optimizasyon problemlerine bir nirengi noktası ve bir mihenk taşı gibi yol gösterici ve değerleyici problem olarak kullanılmaktadır. Problem sonucunu hesaplamak, çok zor olmakla beraber hem tam sonuç hem de "sezgisel (heuristic)" sonuçlar verebilecek birçok çözüm yöntemi bilinmektedir ve pratikte bazen on binlerce şehri ihtiva eden listelerden oluşan problemlerin çözülebileceği bilinmektedir.
Çözüm
Basit bir şekilde:
- Başlangıç için seçebileceği
değişik şehir vardır
- İlk şehirde, satıcının
değişik şehir arasında seçim hakkı vardır
- İkinci şehirde, satıcının
değişik şehir arasında seçim hakkı vardır
- vs.
Dolayısıyla, sonuç olarak satıcının 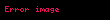

Su an itibarıyla bulunabilmiş en güçlü kesin çözüm sunan algoritma () ile 

Bugüne kadar çözülen en büyük seyyar satıcı problemi 33.810 noktalı bir problemdir ve bir mikroçipin model tasarımı için çözülmüştür. Bundan önceki en büyük seyyar satıcı problemi ise 24.978 noktalıdır ve İsveç'te yerleşimi olan her nokta için çözülmüştür. Bu çözüm, Intel Xeon 2,8 GHz bir işlemcinin 92 yılına denk bir sürede yapılmıştır (öte yandan, 96 bilgisayarlı bir ağ üzerinde çözüldüğünden çözülmesi 3 yıl sürmüştür). Şu anda çözülmeye çalışılan en büyük problem dünya üzerinde kayıtlı yerleşim olan her nokta için en kısa yolun ne olduğudur. Bu problem 1.904.711 şehir içermektedir.[]
Bu problem, seyyar satıcılardan öte internet üzerinde paketlerin yönlendirilmesi gibi konuların çözümünde de faydalı olacağından önemli bir problemdir.
Ayrıca bakınız
- Daha genel hâli için; Araç rotalama problemi
Kaynakça
- ^ William Cook, Daniel Espinoza, Marcos Goycoolea: Computing with Domino-Parity Inequalities for the TSP. 20 Şubat 2012 tarihinde Wayback Machine sitesinde . 2005. (Preprint, pdf; 261 kB)
- İngilizce Wikipedia "Traveling_salesman_problem" maddesi30 Kasım 2011 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
Dış bağlantılar
| Wikimedia Commons'ta Gezgin satıcı problemi ile ilgili ortam dosyaları bulunmaktadır. |
- Seyyar satıcı problemi sitesi7 Şubat 2006 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişme:8.6.2010)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Seyyar satici problemi yoneylem arastirmasi ve teorik bilgisayar bilimi alanlarinda incelenen bir kombinatorik optimizasyon problemidir TanimlamaSeyyar satici problemi su sekilde tanimlanabilir Bir seyyar satici var Bu satici mallarini n displaystyle n sehirde satmak istiyor Ote yandan mantikli bir sekilde bu satici bu sehirleri mumkun olan en kisa sekilde ve her bir sehre maksimum bir kere ugrayarak turlamak istiyor Problemin amaci saticiya bu en kisa yolu sunabilmektir Bu problem bir matematiksel problem olarak 1930 lu yillarda formule edilmistir Optimizasyon konusunda en derin inceleme konularindan biridir Hesaplamanin karmasikligi teorisine gore cozumu NP Tam olan en onemli algoritma problemlerinden biridir Bundan dolayi seyyar satici problemlerini etkin olarak cozebilecek bir algoritma olmadigi kabul edilmektedir Diger bir deyimle en kotu durumda algoritma kullanilirken yapilan hesaplarin sayisinin yani bilgisayar kullanma zamaninin sehir sayilari arttikca ustel olarak artmasi cok olasidir Bazi durumlarda sadece yuz sehirlik liste olmasina ragmen cozum yapilirken cozumun yillar alabilecegi iddia edilmektedir Diger optimizasyon problemlerine bir nirengi noktasi ve bir mihenk tasi gibi yol gosterici ve degerleyici problem olarak kullanilmaktadir Problem sonucunu hesaplamak cok zor olmakla beraber hem tam sonuc hem de sezgisel heuristic sonuclar verebilecek bircok cozum yontemi bilinmektedir ve pratikte bazen on binlerce sehri ihtiva eden listelerden olusan problemlerin cozulebilecegi bilinmektedir CozumBasit bir sekilde Baslangic icin secebilecegi n displaystyle n degisik sehir vardir Ilk sehirde saticinin n 1 displaystyle n 1 degisik sehir arasinda secim hakki vardir Ikinci sehirde saticinin n 2 displaystyle n 2 degisik sehir arasinda secim hakki vardir vs Dolayisiyla sonuc olarak saticinin n displaystyle n degisik tur arasindan secim hakki olacaktir Bu 100 sehirlik bir tur icin bile 9 33 10157 displaystyle 9 33 10 157 degisik tur etmektedir Su an itibariyla bulunabilmis en guclu kesin cozum sunan algoritma ile O n2 2n displaystyle O n 2 2 n zamanda cozulebilmektedir Ornegin 100 sehirlik bir tur icin bu 1 26 1030 displaystyle 1 26 10 30 adim etmektedir Bugune kadar cozulen en buyuk seyyar satici problemi 33 810 noktali bir problemdir ve bir mikrocipin model tasarimi icin cozulmustur Bundan onceki en buyuk seyyar satici problemi ise 24 978 noktalidir ve Isvec te yerlesimi olan her nokta icin cozulmustur Bu cozum Intel Xeon 2 8 GHz bir islemcinin 92 yilina denk bir surede yapilmistir ote yandan 96 bilgisayarli bir ag uzerinde cozuldugunden cozulmesi 3 yil surmustur Su anda cozulmeye calisilan en buyuk problem dunya uzerinde kayitli yerlesim olan her nokta icin en kisa yolun ne oldugudur Bu problem 1 904 711 sehir icermektedir kaynak belirtilmeli Bu problem seyyar saticilardan ote internet uzerinde paketlerin yonlendirilmesi gibi konularin cozumunde de faydali olacagindan onemli bir problemdir Ayrica bakinizDaha genel hali icin Arac rotalama problemiKaynakca William Cook Daniel Espinoza Marcos Goycoolea Computing with Domino Parity Inequalities for the TSP 20 Subat 2012 tarihinde Wayback Machine sitesinde 2005 Preprint pdf 261 kB Ingilizce Wikipedia Traveling salesman problem maddesi30 Kasim 2011 tarihinde Wayback Machine sitesinde arsivlendi Ingilizce Dis baglantilarWikimedia Commons ta Gezgin satici problemi ile ilgili ortam dosyalari bulunmaktadir Seyyar satici problemi sitesi7 Subat 2006 tarihinde Wayback Machine sitesinde Ingilizce Erisme 8 6 2010
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans