Karmaşık analizde, tam fonksiyon veya başka bir deyişle integral fonksiyonu, karmaşık düzlemin tümünde holomorf olan karmaşık değerli bir fonksiyondur. Tam fonksiyonların tipik örnekleri polinomlar, üstel fonksiyon ve bunların toplamları, çarpımları ve bileşkeleridir. Her tam fonksiyon üzerinde yakınsayan ile temsil edilebilir. Doğal logaritma ya da karekök fonksiyonu tam bir fonksiyona .
Liouville teoremi tam fonksiyonlar için önemli bir özelliği ifade eder — sınırlı her tam fonksiyon sabittir. Sonuç olarak, Riemann küresinin (karmaşık düzlem ve sonsuzdaki karmaşık nokta) tümünde tam olan (karmaşık değerli) bir fonksiyon sabittir. Bu yüzden, tam bir fonksiyonun sonsuz noktasında bir tekilliği vardır. Bu tekillik ya kutup noktasıdır ya da esaslı tekillik noktasıdır (aşağıdaki Liouville teoremine bakınız). Eğer esaslı tekillik varsa, fonksiyona aşkın tam fonksiyon denilir, öteki türlü fonksiyon bir polinomdur.
Cebirin temel teoremi'nin şık bir kanıtı için de kullanılabilir. Picard'ın küçük teoremi, Liouville teoreminin epeyce güçlendirilmiş halidir: Sabit olmayan tam bir fonksiyon, tüm karmaşık değerleri alır veya almadığı karmaşık noktalar en fazla bir tanedir. Bu sonraki istisnaya örnek olarak 0 değerini hiçbir zaman almayan üstel fonksiyon verilebilir.
kitaplarının birinde, tipik bir tam fonksiyon olarak seçmiştir.
Tam bir fonksiyonun mertebesi
Tam olan bir 
Bu ifadede 

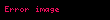
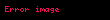

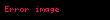
Ayrıca bakınız
Kaynakça
- Ralph P. Boas, Entire Functions, Academic Press, 195413 Ekim 2007 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Karmasik analizde tam fonksiyon veya baska bir deyisle integral fonksiyonu karmasik duzlemin tumunde holomorf olan karmasik degerli bir fonksiyondur Tam fonksiyonlarin tipik ornekleri polinomlar ustel fonksiyon ve bunlarin toplamlari carpimlari ve bileskeleridir Her tam fonksiyon uzerinde yakinsayan ile temsil edilebilir Dogal logaritma ya da karekok fonksiyonu tam bir fonksiyona Liouville teoremi tam fonksiyonlar icin onemli bir ozelligi ifade eder sinirli her tam fonksiyon sabittir Sonuc olarak Riemann kuresinin karmasik duzlem ve sonsuzdaki karmasik nokta tumunde tam olan karmasik degerli bir fonksiyon sabittir Bu yuzden tam bir fonksiyonun sonsuz noktasinda bir tekilligi vardir Bu tekillik ya kutup noktasidir ya da esasli tekillik noktasidir asagidaki Liouville teoremine bakiniz Eger esasli tekillik varsa fonksiyona askin tam fonksiyon denilir oteki turlu fonksiyon bir polinomdur Cebirin temel teoremi nin sik bir kaniti icin de kullanilabilir Picard in kucuk teoremi Liouville teoreminin epeyce guclendirilmis halidir Sabit olmayan tam bir fonksiyon tum karmasik degerleri alir veya almadigi karmasik noktalar en fazla bir tanedir Bu sonraki istisnaya ornek olarak 0 degerini hicbir zaman almayan ustel fonksiyon verilebilir kitaplarinin birinde tipik bir tam fonksiyon olarak secmistir Tam bir fonksiyonun mertebesiTam olan bir f z displaystyle f z fonksiyonunun mertebesi kullanilarak asagidaki gibi tanimlanir r lim supr ln ln M r ln r displaystyle rho limsup r rightarrow infty frac ln ln M r ln r Bu ifadede r displaystyle r 0 displaystyle 0 dan uzakliktir ve M r displaystyle M r z r displaystyle left z right r oldugunda f z displaystyle f z nin maksimum mutlak degeridir 0 lt r lt displaystyle 0 lt rho lt infty ise ayrica tip de asagidaki gibi tanimlanabilir s lim supr ln M r rr displaystyle sigma limsup r rightarrow infty frac ln M r r rho Ayrica bakinizKaynakcaRalph P Boas Entire Functions Academic Press 195413 Ekim 2007 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State