Azərbaycanca
Deutsch
日本語
Lietuvos
සිංහල
Türkçe
Українська
United State
Basit cebir, matematik dersinde öğretilen cebirin en temel kısmıdır. Normalde liselerde öğretilir ve öğrencilerin işlem ve belirli sayılar üzerine kurulu olan aritmetiği anlamalarını sağlar. Cebir, değişken olarak bilinen sabit olmayan değerlerin büyüklüklerini açıklar. Soyut cebir aksine temel cebir, ile ilgilenmez, reel sayı ve karmaşık sayılarla ilgilenir.
Cebirsel gösterim
Cebirsel gösterim, cebirin nasıl yazıldığını açıklar. Belirli kuralları ve dönüşümleri vardır. Örneğin 
ifadesi şu bileşenlere sahiptir:
1 : üs (kuvvet), 2 : katsayı, 3 : terim, 4 : operatör, 5 : sabit,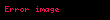 
: değişkenler
Katsayı bir değişken (buna operatör (çarpım işareti) de dahildir) ile çarpılan sayısal bir değerdir. Terimler, toplama veya çıkarma işaretleri, bir katsayı grubunu, sabitleri, değişkenleri, üstelleri birbirlerinden ayrılır.Harfler değişkenleri ve sabitleri ifade eder. Dönüşümlerde alfabenin başındaki harfler (örneğin; 
), genellikle sabitleri ve alfabenin sonundakiler (örneğin ve 
) de değişkenleri ifade etmesi için kullanılır. Bunlar genellikle italik (hafif sağa yatık) olarak yazılır.
Kaynakça
- ^ Richard N. Aufmann, Joanne Lockwood, Introductory Algebra: An Applied Approach, Publisher Cengage Learning, 2010, , 9781439046043, page 78 14 Temmuz 2014 tarihinde Wayback Machine sitesinde .
- ^ William L. Hosch (editor), The Britannica Guide to Algebra and Trigonometry, Britannica Educational Publishing, The Rosen Publishing Group, 2010, , 9781615302192, page 71 2 Aralık 2013 tarihinde Wayback Machine sitesinde .
- ^ James E. Gentle, Numerical Linear Algebra for Applications in Statistics, Publisher: Springer, 1998, , 9780387985428, 221 pages, [James E. Gentle page 183]
Ayrıca bakınız
Dış bağlantılar
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Basit cebir matematik dersinde ogretilen cebirin en temel kismidir Normalde liselerde ogretilir ve ogrencilerin islem ve belirli sayilar uzerine kurulu olan aritmetigi anlamalarini saglar Cebir degisken olarak bilinen sabit olmayan degerlerin buyukluklerini aciklar Soyut cebir aksine temel cebir ile ilgilenmez reel sayi ve karmasik sayilarla ilgilenir ax2 bx c 0 displaystyle ax 2 bx c 0 ikinci dereceden denkleminin cozumu Buradaki a b c x displaystyle a b c x sembollerinin tumu sayilari ifade eden degiskendir Parabolun kirmizi egri cebirsel denklemi y x2 x 2 displaystyle y x 2 x 2 dir Cebirsel gosterimCebirsel gosterim cebirin nasil yazildigini aciklar Belirli kurallari ve donusumleri vardir Ornegin 3x2 2xy c displaystyle 3x 2 2xy c ifadesi su bilesenlere sahiptir 1 us kuvvet 2 katsayi 3 terim 4 operator 5 sabit x y displaystyle x y degiskenler Katsayi bir degisken buna operator carpim isareti de dahildir ile carpilan sayisal bir degerdir Terimler toplama veya cikarma isaretleri bir katsayi grubunu sabitleri degiskenleri ustelleri birbirlerinden ayrilir Harfler degiskenleri ve sabitleri ifade eder Donusumlerde alfabenin basindaki harfler ornegin a b c displaystyle a b c genellikle sabitleri ve alfabenin sonundakiler ornegin x y displaystyle x y ve z displaystyle z de degiskenleri ifade etmesi icin kullanilir Bunlar genellikle italik hafif saga yatik olarak yazilir Kaynakca Richard N Aufmann Joanne Lockwood Introductory Algebra An Applied Approach Publisher Cengage Learning 2010 ISBN 1439046042 9781439046043 page 78 14 Temmuz 2014 tarihinde Wayback Machine sitesinde William L Hosch editor The Britannica Guide to Algebra and Trigonometry Britannica Educational Publishing The Rosen Publishing Group 2010 ISBN 1615302190 9781615302192 page 71 2 Aralik 2013 tarihinde Wayback Machine sitesinde James E Gentle Numerical Linear Algebra for Applications in Statistics Publisher Springer 1998 ISBN 0387985425 9780387985428 221 pages James E Gentle page 183 Ayrica bakinizIkili islem Matematik egitimi Sayi dogrusu PolinomDis baglantilar