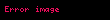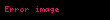Matematikte terim testi, ıraksaklık testi veya ıraksaklık için n'inci terim testi bir sonsuz serinin ıraksaklığını belirlemenin basit bir yöntemidir:
- ise veya limit yok ise, o zaman ıraksar.
Çoğu yazar bu teste isim vermez veya verirlerse de kısa bir isim verir.
Kullanımı
Daha güçlü aksine, terim testi kendi başına bir serinin olduğunu ifade etmez. Bilhassa, testin tersi doğru değildir. Bunun yerine
ise, o zaman
yakınsayabilir de yakınsamayabilir de.
denilebilir. Harmonik seri, terimleri 0'a giden ancak ıraksak olan bir serinin klasik bir örneğidir. Harmonik serilerin daha genel bir sınıfı olan , yani
testin muhtemel sonuçlarını ortaya çıkaran güzel bir örnektir:
- p ≤ 0 ise, o zaman terim testi serinin ıraksak olduğunu söyler.
- 0 < p ≤ 1 ise, o zaman terim testi sonuçsuzdur; ancak seri integral testi ile ıraksaktır.
- 1 < p ise, o zaman terim testi sonuçsuzdur; ancak seri yine integral testi ile yakınsaktır.
Kanıtlar
Test genelde devrik biçimde kanıtlanır:
yakınsarsa, o zaman
olur.
Limit manipülasyonu
sn serini kısmi toplamları ise, o zaman serinin yakınsaması varsayımı, belli bir s için
anlamına gelir. O zaman:
olur.
Cauchy ölçütü
Serinin yakınsadığı varsayımı Cauchy yakınsaklık testini sağladığı anlamına gelmektedir: Her 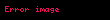
ifadesi n > N ve p ≥ 1 için tutar. p = 1 koymak ise tanımın ifadesini, yani
ifadesini kurtarır.
Kapsam
Terim testinin en basit çeşidi gerçel sayıların sonsuz serilerine uygulanır. Üstteki iki kanıt, Cauchy ölçütünü veya limitin doğrusallığını kullanarak, diğer herhangi bir da geçerlidir.
Notlar
- ^ Kaczor sf.336
- ^ Mesela, Rudin (sf.60) sadece devrik biçimden bahseder ve isimlendirmez. Brabenec (sf.156) n'inci terim testi olarak adlandırır. Stewart (sf.709) Iraksaklık testi demektedir.
- ^ Rudin sf.60
- ^ Brabenec sf.156; Stewart sf.709
- ^ Rudin (sf.59-60) Cauchy ölçütünün başka bir ifadesini kullanarak bu kanıt fikrini kullanır.
- ^ Hansen sf.55; Şuhubi sf.375
Kaynakça
- Brabenec, Robert (2005), Resources for the study of real analysis, MAA,
- Hansen, Vagn Lundsgaard (2006), Functional Analysis: Entering Hilbert Space, World Scientific,
- Kaczor, Wiesława and Maria Nowak (2003), Problems in Mathematical Analysis, American Mathematical Society,
- (1976) [1953], Principles of mathematical analysis (3 bas.), McGraw-Hill,
- Stewart, James (1999), Calculus: Early transcendentals (4 bas.), Brooks/Cole,
- Şuhubi, Erdoğan S. (2003), Functional Analysis, Springer,
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte terim testi iraksaklik testi veya iraksaklik icin n inci terim testi bir sonsuz serinin iraksakligini belirlemenin basit bir yontemidir limn an 0 displaystyle lim n to infty a n neq 0 ise veya limit yok ise o zaman n 1 an displaystyle sum n 1 infty a n iraksar Cogu yazar bu teste isim vermez veya verirlerse de kisa bir isim verir KullanimiDaha guclu aksine terim testi kendi basina bir serinin oldugunu ifade etmez Bilhassa testin tersi dogru degildir Bunun yerine limn an 0 displaystyle lim n to infty a n 0 ise o zaman n 1 an displaystyle sum n 1 infty a n yakinsayabilir de yakinsamayabilir de denilebilir Harmonik seri terimleri 0 a giden ancak iraksak olan bir serinin klasik bir ornegidir Harmonik serilerin daha genel bir sinifi olan yani n 1 1np displaystyle sum n 1 infty frac 1 n p testin muhtemel sonuclarini ortaya cikaran guzel bir ornektir p 0 ise o zaman terim testi serinin iraksak oldugunu soyler 0 lt p 1 ise o zaman terim testi sonucsuzdur ancak seri integral testi ile iraksaktir 1 lt p ise o zaman terim testi sonucsuzdur ancak seri yine integral testi ile yakinsaktir KanitlarTest genelde devrik bicimde kanitlanir n 1 an displaystyle sum n 1 infty a n yakinsarsa o zaman limn an 0 displaystyle lim n to infty a n 0 olur Limit manipulasyonu sn serini kismi toplamlari ise o zaman serinin yakinsamasi varsayimi belli bir s icin limn sn s displaystyle lim n to infty s n s anlamina gelir O zaman limn an limn sn sn 1 s s 0 displaystyle lim n to infty a n lim n to infty s n s n 1 s s 0 olur Cauchy olcutu Serinin yakinsadigi varsayimi Cauchy yakinsaklik testini sagladigi anlamina gelmektedir Her e gt 0 displaystyle varepsilon gt 0 icin bir N sayisi vardir oyle ki an 1 an 2 an p lt e displaystyle a n 1 a n 2 ldots a n p lt varepsilon ifadesi n gt N ve p 1 icin tutar p 1 koymak ise tanimin ifadesini yani limn an 0 displaystyle lim n to infty a n 0 ifadesini kurtarir KapsamTerim testinin en basit cesidi gercel sayilarin sonsuz serilerine uygulanir Ustteki iki kanit Cauchy olcutunu veya limitin dogrusalligini kullanarak diger herhangi bir da gecerlidir Notlar Kaczor sf 336 Mesela Rudin sf 60 sadece devrik bicimden bahseder ve isimlendirmez Brabenec sf 156 n inci terim testi olarak adlandirir Stewart sf 709 Iraksaklik testidemektedir Rudin sf 60 Brabenec sf 156 Stewart sf 709 Rudin sf 59 60 Cauchy olcutunun baska bir ifadesini kullanarak bu kanit fikrini kullanir Hansen sf 55 Suhubi sf 375KaynakcaBrabenec Robert 2005 Resources for the study of real analysis MAA ISBN 0 88385 737 5 Hansen Vagn Lundsgaard 2006 Functional Analysis Entering Hilbert Space World Scientific ISBN 981 256 563 9 Kaczor Wieslawa and Maria Nowak 2003 Problems in Mathematical Analysis American Mathematical Society ISBN 0 8218 2050 8 1976 1953 Principles of mathematical analysis 3 bas McGraw Hill ISBN 0 07 054235 X Stewart James 1999 Calculus Early transcendentals 4 bas Brooks Cole ISBN 0 534 36298 2 Suhubi Erdogan S 2003 Functional Analysis Springer ISBN 1 4020 1616 6
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State