Terminal hızı

Terminal hızı, bir nesnenin bir akışkanın içinde düşerken ulaşabileceği maksimum hızdır. Sürükleme kuvveti (Fd) ve kaldırma kuvvetinin toplamı, nesneye etki eden aşağı doğru yerçekimi kuvvetine (Fg) eşit olduğunda bu hıza ulaşılmaktadır. Cisim üzerindeki net kuvvet sıfır olduğundan, cismin ivmesi sıfırdır.

Aşağı doğru yerçekimi kuvveti (Fg), sürüklemenin (Fd) sınırlayıcı kuvveti ile kaldırma kuvvetinin toplamına eşittir. Nesne üzerindeki net kuvvet sıfırdır. Sonuç, nesnenin hızının sabit kalmasıdır.

Akışkanlar dinamiğinde, bir nesne, içinde hareket ettiği akışkan tarafından uygulanan sınırlayıcı kuvvet nedeniyle hızı sabitse, son hızında hareket etmektedir.

Bir nesnenin hızı arttıkça, içinden geçtiği maddeye (örneğin hava veya su) bağlı olan, üzerine etki eden sürükleme kuvveti de artmaktadır. Belirli bir hızda, direnç veya direnç kuvveti, nesne üzerindeki yerçekimi kuvvetine eşit olmaktadır. Bu noktada nesne ivmelenmeyi durdurmaktadır. Ayrıca, terminal hız (yerleşme hızı da denir) olarak adlandırılan sabit bir hızda düşmeye devam etmektedir. Son hızdan daha hızlı olarak aşağı doğru hareket eden bir nesne (örneğin aşağı doğru fırlatıldığı, atmosferin daha ince bir bölümünden düştüğü veya şekil değiştirdiği için) son hıza ulaşana kadar yavaşlamaktadır. Sürükleme, yansıtılan alana, burada nesnenin yatay bir düzlemde kesitine veya siluetine bağlıdır. Paraşüt gibi kütlesine göre büyük bir projeksiyon alanına sahip bir nesne, bir dart gibi kütlesine göre küçük bir projeksiyon alanına sahip olandan daha düşük bir son hıza sahiptir. Genel olarak, aynı şekil ve malzeme için, bir nesnenin son hızı boyutla birlikte artmaktadır. Bunun nedeni, aşağı doğru kuvvetin (ağırlık) doğrusal boyutun küpüyle orantılı olmasıdır. Ancak hava direncinin yalnızca doğrusal boyutun karesi olarak artan enine kesit alanıyla yaklaşık olarak orantılı olmasıdır. Toz ve sis gibi çok küçük nesneler için, son hız, yere ulaşmalarını engelleyen konveksiyon akımları tarafından kolayca aşılmaktadır. Bu nedenle havada belirsiz süreler boyunca asılı kalmaktadırlar. Hava kirliliği ve sis, konveksiyon akımlarına örnektir.

Örnekler

Terminal hıza ulaşan bir paraşütçünün zamana karşı hız grafiği.

Rüzgar direncine bağlı olarak, örneğin, bir paraşütle atlamacının göbekten toprağa (yani yüz aşağı) serbest düşüş pozisyonundaki terminal hızı saatte yaklaşık 195 km'dir. Bu hız, hızın asimptotik sınır değeridir ve cisme etki eden kuvvetler, terminal hıza yaklaştıkça birbirini daha da dengelemektedir. Bu örnekte, yalnızca yaklaşık 3 saniye sonra terminal hızının %50'si olan bir hıza ulaşılırken, %90'a ulaşmak 8 saniye, %99'a ulaşmak için 15 saniye geçmektedir

Paraşütçü bacaklarını yukarı çekerse daha yüksek hızlara ulaşılabilmektedir (ayrıca bkz. serbest uçuş). Bu durumda, son hız yaklaşık 320 km/sa (200 mph veya 90 m/s) değerine yükselmektedir. Bu, neredeyse avına dalış yapan gökdoğanın son hızıdır. Tipik için aynı terminal hızına ulaşılmaktadır. 1920 ABD Ordusu Mühimmat çalışmasına göre, 30-60 mermisi yukarı doğru ateşlendikten veya bir kuleden düşürüldükten sonra yere dönerken bu hızla aşağı düşüyor.

Rekabet hızında paraşütçüler baş aşağı konumda uçmaktadırlar. Ayrıca, 530 km/sa (330 mph; 150 m/s) hızlara ulaşabilmektedirler. Şu anki rekor, 128.100 fit (39.000 m) yükseklikten atlayarak 13.576 km/sa'ya (8.400 mph; 3.800 m/s) ulaşan Felix Baumgartner'a aittir. Dünya yüzeyinden çok daha düşüktür, bu nedenle düşük bir sürükleme kuvveti oluşturmaktadır.

Biyolog J. B. S. Haldane şu şekilde bir yazı yayınlamıştır:

Fare ve daha küçük herhangi bir hayvan için [yerçekimi] pratikte hiçbir tehlike arz etmez. Bin yardalık bir maden kuyusuna bir fare bırakabilirsiniz. Dibe vardığında hafif bir şok yaşar ve uzaklaşır. Bir sıçan öldürülür, bir adam kırılır, bir at sulanır. Çünkü havanın harekete gösterdiği direnç, hareket eden cismin yüzeyi ile orantılıdır.

Fizikteki kullanımı

Matematiksel terimler kullanılarak, son hız - kaldırma kuvveti etkileri dikkate alınmadan - aşağıdaki eşitlik ile tanımlanmaktadır.

${\displaystyle V_{t}={\sqrt {\frac {2mg}{\rho AC_{d}}}}}$

• ${\displaystyle V_{t}}$ terminal hızını temsil etmektedir.
• ${\displaystyle m}$ düşen cismin kütlesidir.
• ${\displaystyle g}$ yerçekimi ivmesidir.
• ${\displaystyle C_{d}}$ sürükleme katsayısıdır.
• ${\displaystyle \rho }$ cismin düştüğü sıvının yoğunluğudur.
• ${\displaystyle A}$ nesnenin öngörülen alanıdır.

Gerçekte, bir nesne son hızına asimptotik olarak yaklaşmaktadır.

Çevreleyen sıvı tarafından nesne üzerindeki yukarı doğru kuvvet nedeniyle kaldırma etkileri, Arşimet ilkesi kullanılarak dikkate alınabilir: m kütlesi, yer değiştiren akışkan kütlesi pV tarafından azaltılmalıdır. V nesnenin hacmidir. Bu nedenle, bu ve sonraki formüllerde m yerine azaltılmış kütle kullanılmaktadır.

Bir nesnenin son hızı, sıvının özelliklerine, nesnenin kütlesine ve öngörülen enine kesit yüzey alanına bağlı olarak değişmektedir.

Hava yoğunluğu, irtifa azaldıkça, 80 metrede (260 ft) yaklaşık %1 oranında artmaktadır. Atmosferden düşen nesneler için her 160 metrelik (520 ft) düşüş için terminal hızı %1 azalmaktadır. Lokal terminal hıza ulaştıktan sonra düşüş devam ederken hız yerel terminal hız ile değişmek üzere azalmaktadır.

Terminal hız için türetme

Matematiksel terimleri kullanarak, Dünya yüzeyine yakın düşen bir cisme etki eden net kuvvet (sürükleme denklemine göre):

${\displaystyle F_{net}=ma=mg-{1 \over 2}\rho v^{2}AC_{d},}$

v(t) ile t zamanının bir fonksiyonu olarak nesnenin hızı bu formül ile tanımlanmaktadır.

Dengede, net kuvvet sıfırken (Fnet = 0) ve hız limt→∞ v(t) = V_t iken son hıza aşağıfaki şekilde ulaşılır:

${\displaystyle mg-{1 \over 2}\rho V_{t}^{2}AC_{d}=0.}$

V_t için çözümleme

(5) ${\displaystyle V_{t}={\sqrt {\frac {2mg}{\rho AC_{d}}}}.}$

Sürünen bir akışta son hız

Creeping flow past a sphere: , drag force F_d and force by gravity F_g

Akışkanın çok yavaş hareketi için, akışkanın atalet kuvvetleri, diğer kuvvetlere kıyasla ihmal edilebilmektedir. Bu tür akışlara sürünen akışlar denmektedir. Akışların sürünen akış olması için gereken koşul Reynolds sayısıdır, Re << 1. Sürünen akış için hareket denklemi (basitleştirilmiş Navier-Stokes denklemi) şu şekilde verilir:

${\displaystyle {\mathbf {\nabla } }p=\mu \nabla ^{2}{\mathbf {v} }}$

• ${\displaystyle {\mathbf {v} }}$ akışkan hızı vektör alanıdır,
• ${\displaystyle p}$ sıvı basıncı alanıdır,
• ${\displaystyle \mu }$ sıvı viskozitesidir.

Bir küre etrafındaki sürünen akışın analitik çözümü ilk olarak 1851'de Stokes tarafından verilmiştir. Stokes'un çözümünden küre üzerine etkiyen sürükleme kuvveti şu şekilde elde edilmektedir:

${\displaystyle \quad (6)\qquad D=3\pi \mu dV\qquad \qquad {\text{or}}\qquad \qquad C_{d}={\frac {24}{Re}}}$

Reynolds numarası, 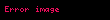${\displaystyle Re={\frac {1}{\mu }}\rho dV}$.

Denklem (6) ile verilen sürükleme kuvvetinin ifadesine Stokes yasası denmektedir.

Denklem (5)'te 'nin değeri değiştirildiğinde, sürünen akış koşulları altında hareket eden küresel bir cismin son hızı ifadesi elde edilmektedir:

${\displaystyle V_{t}={\frac {gd^{2}}{18\mu }}\left(\rho _{s}-\rho \right),}$

${\displaystyle \rho _{s}}$ cismin yoğunluğudur.

Uygulamalar

Sürünen akış sonuçları, okyanus tabanına yakın tortuların çökelmesini ve atmosferdeki nem düşüşlerini incelemek için uygulanabilir. İlke, örneğin yağ, parafin, katran vb. gibi yüksek viskoziteli sıvıların viskozitesini ölçmek için kullanılan deneysel bir cihaz olan düşen küre viskozimetresinde de uygulanmaktadır.

Kaldırma kuvveti varlığında terminal hızı

Settling velocity W_s of a sand grain (diameter d, density 2650 kg/m³) in water at 20 °C, computed with the formula of Soulsby (1997).

Kaldırma etkisi hesaba katıldığında, kendi ağırlığı altında bir sıvının içinden düşen bir cisim, cisme etki eden net kuvvet sıfır olursa, bir terminal hıza (yerleşme hızı) ulaşabilir. Son hıza ulaşıldığında, cismin ağırlığı, yukarı kaldırma kuvveti ve sürükleme kuvveti ile tam olarak dengelenir. Bu durum bize aşağıdaki denklemi vermektedirç

${\displaystyle \quad (1)\qquad W=F_{b}+D}$

• ${\displaystyle W}$ = nesnenin ağırlığı,
• ${\displaystyle F_{b}}$ = cisme etki eden kaldırma kuvvetidir.
• ${\displaystyle D}$ = cisme etki eden sürükleme kuvvetidir.

Düşen cismin şekli küresel ise, üç kuvvetin ifadesi aşağıda verilmiştir:

${\displaystyle {\begin{aligned}\quad &(2)\qquad &W&={\frac {\pi }{6}}d^{3}\rho _{s}g,\\\quad &(3)\qquad &F_{b}&={\frac {\pi }{6}}d^{3}\rho g,\\\quad &(4)\qquad &D&=C_{d}{\frac {1}{2}}\rho V^{2}A,\end{aligned}}}$

• ${\displaystyle d}$ küresel nesnenin çapıdır,
• ${\displaystyle g}$ yerçekimi ivmesidir.
• ${\displaystyle \rho }$ sıvının yoğunluğu,
• ${\displaystyle \rho _{s}}$ cismin yoğunluğu,
• ${\displaystyle A={\frac {1}{4}}\pi d^{2}}$ kürenin öngörülen alanıdır,
• ${\displaystyle C_{d}}$ sürükleme katsayısıdır.
• ${\displaystyle V}$ karakteristik hızdır (terminal hız olarak alınır,).

Aşağıdaki ifadeyi elde etmek için denklem (1)'deki denklemlerin (2-4)'deki denklemlerle değiştirilmesi ile terminal hızı aşağıdaki gibi çözülmektedir.

${\displaystyle \quad (5)\qquad V_{t}={\sqrt {{\frac {4gd}{3C_{d}}}\left({\frac {\rho _{s}-\rho }{\rho }}\right)}}.}$

(1) denkleminde cismin sıvıdan daha yoğun olduğu varsayılmaktadır. Değilse, cisim yerçekimine karşı yukarı doğru hareket edeceğinden, sürükleme kuvvetinin işareti negatif yapılmalıdır. Örnekler, bir şampanya bardağının dibinde oluşan kabarcıklar ve helyum balonlarıdır. Bu gibi durumlarda terminal hız, yükselme hızına karşılık gelen negatif bir değere sahip olmaktadır.

Ayrıca Bakılabilir

Kaynakça

1. ^ . NASA Glenn Research Center. 20 Ekim 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Mart 2009. 
2. ^ Riazi, A.; Türker, U. (January 2019). "The drag coefficient and settling velocity of natural sediment particles". Computational Particle Mechanics. doi:10.1007/s40571-019-00223-6. 
3. ^ ^{a b} Huang, Jian (1999). . The Physics Factbook. Glenn Elert, Midwood High School, Brooklyn College. 24 Ocak 2017 tarihinde kaynağından arşivlendi. 
4. ^ . U.S. Fish and Wildlife Service. 20 Aralık 2007. 8 Mart 2010 tarihinde kaynağından arşivlendi. 
5. ^ The Ballistician (March 2001). . W. Square Enterprises, 9826 Sagedale, Houston, Texas 77089. 31 Mart 2008 tarihinde kaynağından arşivlendi. 
6. ^ {{Akademik dergi kaynağı |soyadı=Haldane |ad=J. B. S. |yazarbağı=J. B. S. Haldane |tarih=March 1926 |başlık=On Being the Right Size |dergi=Harper's Magazine |url=

Ekstra Kaynaklar

• Terminal Velocity 23 Şubat 2009 tarihinde Wayback Machine sitesinde . - NASA site
• Onboard video of Space Shuttle Solid Rocket Boosters rapidly decelerating to terminal velocity on entry to the thicker atmosphere 27 Kasım 2015 tarihinde Wayback Machine sitesinde ., from 2.900 mil/saat (Mach 3,8) at 5:15 in the video, to 220  mph at 6:45 when the parachutes are deployed 90 seconds later—NASA video and sound, @ io9.com.
• Heywood Tabloları yaklaşımıyla, tüm gerçekçi Reynolds Sayılarında bir kürenin terminal çökelme hızı.(Terminal settling velocity of a sphere 28 Ocak 2021 tarihinde Wayback Machine sitesinde .)