Termodinamiğin(Isıldevinimin) ikinci yasası, izole sistemlerin entropisinin asla azalamayacağını belirtir. Bunun sebebini izole sistemlerin termodinamik dengeden (maksimum entropi aşaması) spontane olarak oluşmasıyla açıklar. Buna benzer olarak sürekli çalışan makinelerin ikinci kanunu imkânsızdır.
Termodinamiğin ikinci yasası deneysel olarak bir ısı bilgisi önermesi olarak kabul edilir fakat bu yasa altında yatan istatistiksel kuantum mekaniğiyle anlaşılabilir ve açıklanabilir. İstatiksel mekanik literatüründe entropi, makroskopik evrelerde mikroskobik gruplaşmaların ölçümü olarak ifade edilir. Çünkü ısıbilgisinin denge, dengede olmayan duruma göre büyük miktarda mikroskopik dizilişe sahiptir. Bu maksimum entropiye sahiptir ve ikinci yasayı takip eder çünkü düzensiz yalnız değişim kısmen sistemin ısı bilgisinin dengesini geliştirmesini sağlar.
Zamana bağlı bir ifade olarak; sıcaklık, basınç ve kimyasal potansiyel ısıbilgisi dengeye doğru izole edilmiş ve yerçekiminin önemsiz olduğu sistemde azalır.
İkinci yasa farklı birçok şekilde açıklanabilir ama ilk formülasyon 1824 yılında Fransız bilim insanı Sadi Carnot tarafından yazılmıştır. İkinci yasanın ilk ifadeleri yalnızca yatay düzlemde (yerçekimisiz alanda) doğrudur. Ikinci yasa, iç enerji U’ ya eşit olarak kapsamlı özelliklerin fonksiyonu olarak yazılabilir. (Kütle, hacim, entropi,)
Tanımı
Termodinamiğin birinci yasası, termodinamik enerjinin (iç enerji olarak da bilir bütün ısıbilgisi sistemler bilinmeyen klasik mekanikler hariç) basit tanımını ve doğadaki enerji korunumunu sağlar.
Birinci yasadaki enerji konsepti doğal süreçteki gözlemleri hesaplayamaz. Örneğin ısı her zaman istemsizce yüksek sıcaklıktan düşük sıcaklığa doğru akar (dışarıdan iş yapılmadığı sürece). Birinci yasa başlangıç ve son durumlardaki değişimin simetrik olduğunu açıklar. Bunun açıklanmasındaki anahtar durum termodinamiğin ikinci yasası boyunca yeni fiziksel özelliğin tanımı entropidir. Tersine çevrilebilir durumda, entropideki sonsuz küçük artış (dS), ısı transferindeki sonsuz küçük değişimin (δQ) kapalı sistemdeki sıcaklığa (T) bölümümden elde edilebilir.
Korunumlu entropi sistemindeki iç ısıbilgisi denge zamana bağlı değildir. Korunumlu sistem birbirinden ayrılmış başlangıç sistemlerden oluşur ama hepsi kendi dengesine sahiptir. Parçacıklar tekrar hareket ettirilirse önceki sistemler genel bir etkileşim içinde olacaktır ve kendi yeni son ısıbilgisi sistemini oluşturacaktır. Başlangıç entropiler son entroplerden azdır. Eğer başlangıç entropilerinin hepsi aynı değerdeyse, başlangıç ve son entropileride aynı olacaktır.
Vücuttaki temel denge başkasıyla, kesinlikle birçok emprik sıcaklık ölçüsü vardır. ısıbilgisi sistemin arasındaki temel denge eşit derecelerde sonlanır. Isıbilgisinin başlangıç yasası kısa durumlarda iki ortamın aynı derecelerde recogne etmesine izin verir.
İkinci kural, ünlü bir sıcaklık ölçeğine izin verir. Bu ölçek kesin, ısıbilgisi sıcaklık ve herhangi bir özel, bağımsız ısıbilgisi sistemin özelliklerini tanımlar.
Isıbilgisinin 2. Kuralı birçok özgül yolla açıklanabilir. Bunların en önemlilerin durumu: “Rudolph Clasius” (1854), “Lord Kelvin” (1851) ve “Constantin Caratheodory” (1909) tarafından açıklanmıştır. Bu ifadeler, kesin süreçlerin olanaksızlığı ilkesine dayanarak genel fizik terimlerine dayanır. Clasius'un ve Kelvin'in açıklamaları eşdeğer olarak kabul edilir.
Carnot’s prensibi
Isıbilgisinin 2. Yasasının tarihsel kökeni 'dir. Bu prensibi, Carnot makinesi döngüsünü gösterir. Carnot makinesi; ısı ve iş aktarımlarının birbiri içinde sürekli kendi iç ısıbilgisi dengede almasını düzenler. Bu makine, ısı makinelerinin verimliliğiyle ilgilenen mühendislerin ilgisini çeker, idealize edilmiş bir aygıttır. Carnot’s prensibi, kalasik teorisi caddice anlaşıldıktan sonra ve termodinamiğin 1. Kanununun ve entropinin matematiksel izahından önce tanıtılmıştır. 1. Kanunun yorumlanması. Termodinamiğin 2. Kuralının anlaşılmasını kolaylaşmıştır. Bu, bugün için bile hâlâ geçerlidir.
Quasi-statik veya tersinir Carnot döngüsünün verimliliği, sadece iki ısı kaynağının sıcaklığına ve çalışan kaynağın serbestliğine bağlıdır. Bir Carnot makinesi, bu iki sıcaklığın kullanılmasıyla en verimli şekilde kullanılabilir.
Clausius ifadesi
Alman bilim insanı , ısı ve iş aktarımlarını inceleyerek, ısıbilgisinin 2. Yasasını kurmuş oldu. (1850) onun bu yasayı açıklaması "Clausius ifadesi" olarak bilinir: (1854 Almanya)
Isı, hiçbir zaman soğuk bir cisimden ılık bir cisme bir takım değişiklikler olmadan geçmez.
Isı, sıcak bölgelerden soğuk bölgelere aniden ve iş yapmadan geçemez. Bu, sıradan bir donma olayıyla kanıtlanabilir. Bir dondurucu içinde, ısı soğuktan sıcağa ve sadece dışarıdan bir kuvvet uygulandığında geçebilir.
Kelvin ifadesi
Lord Kelvin 2. kanunu şu şekilde ifade etmiştir:
Donuk meteryal aracılığıyla, etrafındaki en soğuk nesne vasıtasıyla soğutulmuş herhangi bir maddeyi türetmek imkansızdır.
Planck prensibi
1926’da, Max Planck termodinamik temelleri hakkında önemli bir makale yazdı.
- Bu makaleyle kapalı sistemlerdeki iç enerjinin bir isochosic adiabatic süreçle arttığını gösterdi.
Bu formülasyon, ısı ve sıcaklıktan ya da entropiden bahsetmedi ve dolaylı olarak bu kavramlara bağlı değildi; fakat 2. Kanunun içeriğini taşıyordu. Bağlı olduğu ifade: “sürtünme kuvveti asla pozitif iş yapamaz” dı. Planck, kelimelerin eski biçimlerini kullanarak şunu yazdı: “Isının sürtünme tarafından üretimi tersinir değildir.”
Caratheodory prensibi
, ısıbilgisi saf matemetic aksiyemura bağlı olarak formüle etti. Onun 2. Kanunla ilgili ifadesi "Caratheodory prensibi" olarak bilinir.
Caratheodory adyabatik erişebilirlik kavramını ilk kez tanımladı ve klasik ısıbilgisinin alt kategorilerini sınıflandırdı.
Bunlar “geometric ısıbilgisi” olarak adlandırılır ve enerjinin quasi-statik olarak transferinin miktarı prensibini taktik Eder. (Çünkü ısı holonomic bir süreçtir. 
Caretheodory’nin Prensibi 2. Kanunu ifade Eder ve Clausius ya da Kelvin-Planck ifadesine eşdeğerdir. 2. Kanunun tümiçeriğini almak için Caratheodory Prensibi, Planck Prensibi ne ihtiyaç duyar. Isokharic iş, her zaman başta kendi iş ısıbilgisi denkliğine sahip kapalı sistemin iç enerjisini artırır.
Clausius ve Kelvin ifadelerinin eşitliği

Bir motorun Kelvin ifadesiyle çalıştığını düşünelim. Mesela biri ısıyı tüketiyor ve bunu bütünüyle bir “iş’e döünüştürüyor. Bu yeni yapılmış makinenin net ve biricik etkisi iki motor içerir. Aktarılmış ısı:
Sonuç olarak Kelvin ifadesinin aykırılığı, Clausius ifadesinin aykılırlığı anlamına da gelir; yeni Clausius ifadesi, Kelvin ifadesini de ima eder. Bunu ayrı şekilde Kelvin ifadesi, Clausius ifadesini ima Eder şekilde de bulabiliriz. Bu yüzden bu iki ifade eşdeğerdir.
Yerçekimi sistemleri
Yerçekimsiz sistemlerde, nesne her zaman pozitif ısı kapasitesine sahiptir; bu da sıcaklığın enerji ile yükseleceği anlamına gelir. Bu yüzden, enerji yüksek sıcaklıktaki nesneden düşük sıcaklıktaki nesneye geçtiğinde kaynak sıcaklık düşer. Buna rağmen lavabo sıcaklığı yükselir. Sonuç olarak; sıcaklık farklılıkları zamanla azalma eğilimindedir.
Ancak, bu yerçekimi kuvvetinin önemli olduğu sistemlerde her zaman geçerli olan bir durum değildir. Kara delikler en göze çarpan örneklerdir ve teoriye göre kara delikler negatif ısı kapasitesine sahiptirler. Kara deliklerin büyüklükleri arttıkça, sahip oldukları enerji de artar ama sıcaklıkları düşer. Sonuç olarak, samanyolundaki süper büyük kara deliğin sıcaklığı 10-4K varsayılır, bu sıcaklık kozmik mikrodalga arka plan sıcaklığı olan 2,7 K'den çok düşüktür, fakat bu kara deliğin düşük olan sıcaklığı daha çok azalır çünkü kozmik mikrodalga arka plan fotonlarını absorbe ettiğin için kütlesi artar. Bu yüzden yerçekiminin olduğu ortamlarda kütle ve enerji eşit olarak dağılmaz.
Sonuçlar
Sürekli hareket yasası
İkinci yasanın oluşturulmasından önce, sürekli hareketli makinelerinin icadıyla ilgilenen pek çok insan, makinenin gücü ile sistemin büyük iç enerjisinin farkını alarak ısıbilgisinin birinci yasasının kısıtlamalarından kaçınmaya çalışmışlardır. Bu tür makinelere “devridaim makinesi” denir. İkinci kanun bu makinelerin imkânsızlıklarını açıklamıştır.
Carnot kuramı
Carnot teoremi (1824) her makineyi maksimum verimlilikle sınırlandırır. Verimlilik yalnızca sıcak ve soğuk termal rezervuarlar arasındaki sıcaklık farkına bağlıdır. Carnot kuramı aşağıdaki ifadelere dayanmaktadır:
- İki ısı rezevuarı arasındaki tek yönlü bütün ısı motorları, aynı iki rezervuar arasındaki bir Carnot motorundan daha az verimlidirler.
- İki ısı rezervuarı arasındaki tek yönlü bütün ısı motorları, aynı iki rezervuar arasındaki bir Carnot motoruyla eşit verimliliktedirler.
Carnot’un ideal modelinde kalorik ısı, tersinir hareket döngüsünü eski haline çeviren işe dönüştürüşür. Ancak Carnot, mekanik işe dönüşmeyen ısı kayıplarının olduğunu varsaymıştır. Sonuç olarak Carnot döngüsünün çevrilebilme özelliğini gerçekleştiren gerçek ısı makinesi yoktur ve bu makine çok verimsizdir.
Clausius eşitsizliği
Clausisus teoremi (1854) döngü sürecine dayanır.
Eşitlik tersinir durumu gösterir ve “<” işareti tersinemez durumlarda yer alır. Tersinir durum entropi hal fonksiyonunu açıklamak için kullanılır. Çünkü döngüsel işlemlerde hal fonksiyonunun değişimi sıfırdır.
Termodinamik sıcaklık
Herhangi bir ısı motoru için verimlilik:
A: birim döngüde yapılan iş Carnot önermesi tersinir aynı iki ısı rezervuarlarını çalıştıran tersinir makinelerin eşit verimlilikte olduğunu ifade eder. Sonuçta T1 ve T2 sıcaklıklarında çalışan herhangi tersinir ısı makinesi bu sıcaklıklarda aynı verimlilikte olmak zorundadır. Bu yüzden verim sıcaklığa bağlı fonksiyondur.
Ayrıca T1 ve T3 sıcaklıklarında çalışan tersinir bir ısı makinesinin T1 ve ara sıcaklık olan T2 arasındaki verimliliğiyle T2 ve T3 arasındaki verimliliği eşit olmak zorundadır.
Suyun üç sıcaklık noktalarından 
Sonuçta ısıbilgisi sıcaklık,
f fonksiyonu ısıbilgisi sıcaklık fonksiyonu varsayılır,
,
Ve referans sıcaklık T1 ‘in değeri 273,16 olur.
(Herhangi referans sıcaklığı ve diğer pozitif sayısal değerler Kelvin cinsinden olmalıdır.).
Entropi
Clausius a göre aşağıdaki eşitlik tersine de eşitlenebilir.
Bu demektir ki 
Boylece durum foksiyonu olan ‘entropy’ aşağıdaki gibi tanımlayabiliriz.
Bununla birlikte yukardaki formülün integralini alarak sadece entropy’nin farkını elde edebiliriz. Mutlak değeri elde etmek için muhteşem kristalle içinmutlak sıfırda s=0 olan ısıbilgisinin 3. Yasasına ihtiyacımız vardır.
Herhangi çevrilemeyen süreçte, entropy bir durum foksiyonu olduğu için gerçek olmayan cevrilebilen süreçte birlikte başlangıç ve terminal durumları arasında bağlantı kurabiliriz.
Şimdi cevrilebilen süreci çevir denilen cevrilemeyen süreçte kombin et ve Clausius eşitsizliğine başvur.
- Böylece
Eşitlik dönüşümün çevrilebildiği yerlerde olur.
Eğer sürec ısısız bir süreçse 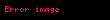

Ekserji, mevcut kullanılabilir iş
Önemli ve idealleştirilmiş özel durum ikinci yasa olan isale edlimiş sisteme (tüm sistem veya evrensel) başvurulmak içindir. Bu işlem iki parttan oluşur. Bunlar ilgilenilen alt-sistem ve çevresel alt-sistemdir. Bu çevresel limitsiz sıcaklık haznesi olarak düşünülebilir.
TR sıcaklıgı ve PR basıncı altında. Ayrıca ne Kadar ısı transefer olsa da sub-systeme sıcaklık her zaman TR kalır ayrıca hacim ne kadar degişsede PR de her zaman sabit kalır.
Ne değişiklik olursa olsun dS ve dSR de ikici yasaya göre Stot olan isole total sistem azalmamaktadir.
Termodinamiğin ilk yasasına göre dU değişimi alt-sistemin iç enerjisinde eşittir su-systeme eklenilen toplam ısı δq eksi alt-sistem tarafından yapılan herhangi iş δw ve artı alt-sisteme giren herhangi net kimyasal enerji d ∑μiRNi yani,
(μiR kimyasal türlerin kimyasal potansiyelleri dışçevrede) şimdi rezervuarı terk eden ısının alt-sisteme girişi
Herhangi alt-sistem tarafından net iş δw uymalıdır ki
Bu kullanışlıdır ayırmak için alt-sistem tarafından yapılan işi δw ve alt-sistem tarafından yapılan işi δwu ve alt-sistem tarafından yapılan pR dV genişler dış çervre basıncına karşı. Aşağıda verilen ilişki kullanışlı iş için verilmiştir.
ısıbilgisi potansiyelin tam türevini tanımlamak için alt-sistemin mevcut veya exergy E si demek uygundur.
Bu yüzden ikinci yasa ima eder herhangi subsystemine ve limitsiz sıcaklık ve basıncına ayrılmış süreç için
İkinci yasa tahmin eder E deki azalışı değişmeyen ve değişen süreçler için
Eşdeğer olduğunda
Bu açıklama 2.yasayı faydalı hale getirmek için desing motor çalışmasına makroskopıc değerlere izin verir. Bu değişiklikler referans durumuyla dengeye ulaşan durumlar altındaki sistemler tarafından tahmin edelir. (Bakıncı2.yasa etkisi).bu yaklaişım 2. yasanın mühendislik pratiklerinde çevre hesaplarında ekoloji sistemlerinde ve öbür hesaplarda yarar sağlar.
Tarihçe
Isının mekanik işe dönüşümüyle ilgili ilk teori Nicolas Leonard Sadi Carnot tarafından 1824 yılında ortaya atıldı. Carnot ilk kez, bu dönüşümün verimliliğinin makine ile çevresi arasındaki sıcaklık farkına bağlı olduğunu fark etti.
Rudolf Clausius, Prescott Joule’in enerjinin korunumu hakkındaki çalışmalarını da göz önünde bulundurarak 1850 yılında ikinci kanunu formülize etti. Bu kanuna göre, bugün bilinenin aksine, ısı kendiliğinden soğuktan sıcağa doğru akmazdı. Buradan hareketle Rudolf, entropinin tanımını ve Sadi Carnot’un ilkelerini tanımlayabildi.
19. Yüzyılda yayımlanan Kelvin Planck’ın açıklaması şöyleydi: “Hiçbir cihaz tek başına bir rezervuardan ısı alarak periyodik olarak çalışamaz ve iş elde edemez.” Bu açıklama Clausius’un açıklamasıyla eşdeğerdi.
Boltzmann’ın yaklaşımı için ergodik hipotez de oldukça önemliydi. Bu hipotez şöyle söylüyordu: “Küçük alanlardaki bölgelerin evrelerinin gerçekleşmesi için gereken zaman, bu bölgenin hacmiyle doğru orantılıdır.” Aynı zamanda ortalama zaman ve statistik grupların ortalaması da eştir.
Sadece klasik sistemlerde değil, quantum mekaniğinde de entropiyi maksimuma çıkarma eğilimi olduğunu görebiliriz. Bu yüzden ikinci kanunda verilen ilk koşullar düşük entropiyle verilir. Sonuçlar üst sınıf izole edilmiş quantum sistemleri için geçerli olur. (Örneğin konteynr içindeki gaz) Bütün sistemde hiç entropi olmasa ve sistem saf olsa bile gaz ve konteynır arasındaki karmaşıklık gazın yerel entropisindeki artışı verir. Bu sonuç quantum ısıbilgisinin en önemli sonucudur.
Bugün, evrenin ilk zamanlarında neden düşük entropiye sahip olduğunu anlamak için oldukça çaba harcanıyor.
Yasal olarak geçersiz açıklama
İkinci kanun birkaç maddeyle özetlenebilir;
- Tek başına bir rezervuar kullanarak periyodik bir iş elde etmek imkânsızdır. (Kelvin, 1851)
- Isıyı motor kullanarak sıcaklığın az olduğu yerden çok olduğu yere aktarmak imkânsızdır. (Clausius, 1854)K
- Eğer ısıbilgisi iş için sonlu bir oran kullanılıyorsa, sonsuz bir enerji kullanılmıştır.
Matematiksel açıklama:

1856 yılında Rudolf Clausius “ısının mekanik kuramının ikinci ana önermesi” adını verdiği kuramını şu şekilde açıkladı:
Q=ısı, T=sıcaklık ve N=karşılığı verilmemiş dönüşümlerin eşdeğeri 1865’de Clausius bu eşdeğeri entropi olarak tanımladı. Clausius sonuçta şu yargıya vardı: “Evrenin entropisi maximum olma eğilimindedir.” Bu önerme ikinci kanunun en bilinen kısmıdır.Bu tanım çok basit durabilir ancak tabii ki kompleks bir tanımın sadeleştirilmiş halidir. Zaman varyasyonu açısından, ikinci kanunun matematiksel ifadesi
S=Sistemin entropisi T=zaman Bu eşitlik geri dönüşebilen süreçler için kullanılır. Eğer süreç geri dönemezse >-işaret alır. İzole edilmiş sistemler için ikinci kanunun alternatif bir formülü vardır:
eğer
ise.
=entropi oranlarının toplamı
Bu formülün avantajı entropi üretiminin etkilerini göstermesidir. Entropi üretimi oranı makinelerin etkisi açısından çok önemlidir. İkinci kanunun kapalı sistemler için formülü:
Eğer
ise.
Q=sisteme akan ısı.
: Isının sisteme girdiği noktadaki sıcaklık
Eğer sisteme belirli noktalardan ısı verilirse, bu değerlerin toplamının alınması gerekir. Açık sistemler için denklem (bileşen değişim imkânı var.)
Ancak
Buradaki, 
İstatistiksel mekanikte ikinci yasa için verilen açıklamada; maddenin atom ve moleküllerden oluştuğunu ve bunların da sabit bir yörüngede hareket halinde olduğu varsayımını kabul ederiz. Belirli durumlarda ve hızlarda sistemdeki her bir parçacık için verilen durumun adı sistemdeki ‘microstate’ (anlık durum) olarak adlandırılır ve sabit hareketten dolayı, sistem kendi ‘microstate’ini sürekli yeniliyor. İstatistiksel mekaniğin bir başka varsayımı ise dengede olan sistemlerde her bir ‘microstate’in oluşma ihtimali birbirine eşit olur ve bu varsayımdan yola çıkılacak olunursa ikinci yasanın mutlaka istatistiksel bir görüşe de sahip olması gerektiği kanısına varılabilir. N’nin sistemdeki parçacık sayısı olduğunu düşünürsek, istatistiksel değişim miktarını da 1/√N ile hesaplayabiliriz. Günlük hayatta, çıplak gözle görebildiğimiz olayları düşündüğümüzde, ikinci yasanın işlev dışı kalma ihtimali sıfır. Ancak, az miktarda parçacığı olan sistemler için, ısıbilgisi kat sayılar (entropi dâhil), ikinci yasanın kuramda öngördüğü rakamlara göre ciddi bir sapma gösterebilir. Isıbilgisi kuramı istatistikler varyasyonlarla ilgilenmez.
İstatistiksel mekaniğin kökeni
Loschmidt paradoksuna rağmen, ikinci yasanın kökeninin geçmişe dair bazı varsayımlara sahip olması gerekmektedir. Tabi sistemin geçmişte bazı durumlarda bağımsız hareket ettiği de olmuştur. Bu durum basit bir olasılık hesabıyla hareket etmemize imkân sağlar. Bu durum limit durumu olarak da bilinir ve ikinci yasa, eninde sonunda başlangıç değerinin neticesinde ortaya çıkmıştır hatta muhtemelen evrenin oluşması ile sonuçlanan büyük patlamanın bile başında.
Verilen varsayımlardan yola çıkıldığında, istatistiksel mekanikte bahsedilen ikinci yasa tam anlamıyla doğru varsayılmamaktadır. Bunun yerine temel bir kavramın sonucu olarak kabul edilir. İkinci yasanın ilk kısmında bahsedilen ısıca yalıtılmış sistemlerin entropisi sadece öncelikli denk olasılığın göz ardı edilebilecek bir kısmını artırır varsayımı ancak ısıl denge halindeki bir sistemi kısıtladığımızda ortaya çıkar. Isıl dengedeki izole bir sistemin entropisinin depoladığı enerji miktarını 
İle
arasındaki kısa aralıktaki kuantum durumlarının sayısıdır.
İse gözle görülür derecede fakat küçük bir miktar enerji aralığını simgeler. Kesin bir dille konuşmak gerekirse entropimiz seçtiğimiz
değerine bağlı olarak değişim gösterir. Yalnız, ısıbilgisi limiti düşündüğümüzde (sistemin ulaşabileceği maksimum genişlik) seçtiğimiz belirli bir entropi (hacmi ve kütlesi belirli)
değerinden etkilenmez.
Farz edelim ki boyutu belirli bir sayıda değişkenle sabit tutulmuş izole bir sistemimiz var. Bu değişkenler, sistemin hacmini, kütlesini ya da pistonların konumunu belirliyor olabilir. 

Eğer değişken başlangıçtan itibaren sabit bir değere sahipse ve yeni dengeye an itibarıyla ulaşılmışsa 
Isıl dengede, iç enerji aralığı 



İkinci yasanın ikinci bölümünde de belirtildiği üzere, geri dönüşümü mümkün olan yöntemlerdeki entropi değişimi şekildeki gibidir:
Bu durumda sıcaklık ise,
Sistemde rolü olan bazı dış değişkenler de mevcut. Genel olarak bunların sistemi değiştirme imkânı var çünkü enerji dışarıdan sağlanır ve sistem için her şey demektir. Kuantum mekaniğinin ısı değişimsiz kuramına göre, neredeyse hiç değişmeyen bir sistemin durumunun limitini aldığımızda, sistemin enerji özünde bir değişim olmaz. Genel haliyle kuvvet, X, dış etkenleri ayarlayan değişken ise x olarak gösterildiğinde 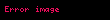

Genişliği boyunca sistem herhangi bir enerji durumunda olabileceği için, sistemdeki genel kuvveti tahmini değerler içinde yazacak olursak;
Ortalama değeri değerlendirecek olursak, 




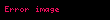
Bu açılımı entropinin türeviyle bağdaşlaştırabiliriz. Denklemde x i x + dx diye değiştirdiğimizi varsayalım. Bu durumda 


Yukarıdaki denklem ele alındığında eğer 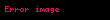



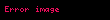
ile ifade edilir. Elde edilen sonuç ise
değerine yapılan net katkıyı gösterir. Eğer
değerden daha yüksekse, E ile
arasında bir değere sahip enerji açığa çıkacaktır.
ve
toplamlarda da sayılan enerji değerleri özetlenecek olursa şu şekilde gösterilebilir:
değerinin logaritmik türevi ise;
İlk terim bazı durumlarda sınırları aşabileceği için alternatif olarak kullanabileceğimiz,
Ve
Bu ikisini bir araya getirmeye çalıştığımızda ise elimize geçen denklem;
Kanonik set ile ifade edilen sistemlerin türevleri
Sisteme giren ya da sistemden çıkan herhangi bir ısı var ise, denge halinde bu ısıyı T ile gösterip, bu ısının sistemdeki belirli yerlere dağılma olasılığının Kanonik Set ile bulunuşu;
Temel olasılık hesabından bilindiği üzere bağımsız bir olayda meydana gelmesi ihtimal dâhilinde olan olayların olasılıkları toplamı 1 etmelidir. Bizim denklemimizde de Z değerlerin toplamının 1de buluşmasını sağlayan temel faktördür. Bu tarz fonksiyonlara da ayrılma fonksiyonu denir. Dış etkenlere bağımlı ısının değişimi ve bunun enerji seviyesine olan katkısını gösteren genel formül;
Bu denklemden
değerini elde ettiğimizde elimizde kalan son değer,
Kuantum mekaniğinin birleştiriciliği
Kuantum mekaniğinin temel yapıtaşlarından biri olan ikinci yasaya baktığımızda geçiş olasılık matrisi ve zamanla gelişen bir birim var. İkinci yasanın bu denli geniş kapsamlı olması onu bir bakıma diğer önerme ve yasaların birleştiricisi de yapar. Genellenebilirliği ve birleştiriciliği açısından herhangi bir ileri kanıta veya desteğe ihtiyacının olmaması evrensel genelgeçer bir üne ve güvene sahip olmasının da bir nevi kanıtıdır.
Dengede olmayan durumlar
Termodinamik analiz amacıyla yaklaştığımızda aslında uzay zaman çizgisinden rastgele seçilmiş herhangi bir olayın ısıbilgisi dengede olduğu düşünülür. Daha geniş bir perspektiften bakıldığında ise uzay-zaman çizgisinde bulunan, kısacası evrendeki hiçbir şey tam anlamıyla ısıbilgisi denge halinde değildir hiç de olmamıştır. Bir diğer ayrıntı ise termal dengedeki bir sistemin istatistiksel olarak denge durumundan çıktığı anlar olması doğaldır. Bazı karşılaşması güç olaylarda ise, sıcak parçacıkların soğuk parçacıklardan enerji çaldığı ve bu sayede ortamdaki sıcak kısmın daha sıcak soğuk kısmın ise giderek daha soğuk bir hal aldığı gözükmüştür, son derece kısa bir zaman aralığında olsa bile.
Fiziğin dâhil olduğu ve gerçekleşmesi kâğıt üzerinde mümkün olan bazı olaylar vardır ki bilindik ısıbilgisinin denge kurallarının çok ötesinde davranış sergileyen. Dalgalanma önermesi ise bir sistemin dengeden uzak kaldığı süre zarfı boyunca entropisindeki değişim miktarının olasılığının rakamsal olarak yaklaşık bir değerini verir.
Geçmişten bugüne
Isıbilgisinin ikinci yasası bir fizik yasasıdır ve geri dönüşlü zaman kavramını kapsamaz. Aslında geçmişte bu yasanın geliştirilmesi açısından zamanda ileri ve geri gidildiğinde ne gibi farklılıklar olabileceğine dair bir açıklama eklenilmesi gerektiği önerilse de günümüze kadar pek bir değişim sergilememiştir.
İhtilaflar
Maxwell’in İblisi
James Clerk Maxwell, A ve B şeklinde ikiye bölünmüş bir konteynır hayal etmiştir. İki parça da eşit miktarda ve eşit sıcaklıktaki aynı gazla doldurulmuş ve yan yana bekletilmektedirler. İki taraftaki molekülleri de izlerken hayali iblisin iki tarafta da savunma yaptığını görür. A’daki iblis daha hızlı hareket ettiğinde B’ye uçan moleküller olur ve A yavaşladığından B zaman içinde daha fazla ısınır ve A’daki ısı düşer. Bu ısıbilgisinin ikinci yasasına göre tamamen zıt bir durumdur.
Loschmidt paradoksu
Loschmidt paradoksu geri döndürülme paradoksu olarak da bilinir. Zamanla simetrik dinamiklerin geri döndürülebilen işleme bir faydası olma ihtimalinin düşünülmesine karşı çıkılmaktadır. Bu bizi, çıplak gözle işleyişini görebildiğimiz sistemlerin davranışlarını açıklamak adına ısıbilgisinin ikinci yasasını kullanmak için bilinen bütün yöntemlerden bir adım daha öne götürmektedir. Bu yöntemlerin neredeyse hepsi kuramdan gücünü almakla beraber bazıları kendi aralarında çelişmektedir. Bu yüzdendir ki onlara paradoks deniyor.
Gibbs paradoksu
İstatistiksel mekanikte, birbirinden ayrılabilen parçacıklardan oluşan ideal gazın entropisinin basit bir türevini aldığımızda bunun ısıbilgisinin ikinci yasasının bazı kurallarını çiğnemesinin yanı sıra kanonik sete dayanması ise bizi bu paradoksun Gibbs paradoksu olarak adlandırmaya itmektedir.
Parçacık türünün entropiyi direkt olarak etkilemediği fark edildiğinde bu paradoks durdurulmuştur. Bilindik bir tabir ile bu, kuantum mekaniği ile bağdaştırılan ve parçacıkların birbirinden farksızlığı ile açıklanan bir tanımlamadır.
Yineleme teoremi
Yineleme kuramı der ki belirli sistemler, üzerlerinden yeteri miktarda uzun bir zaman geçtiğinde başlangıç durumlarına son derece yakın bir konuma gelirler. Bu yenileme zamanı yenilenene kadar akıp giden zaman 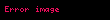
Kâinatın geleceği
Geçmişten gelen bir uyarı olarak evrendeki entropi miktarı zaman içinde giderek arttığı için, etrafımızdaki enerji miktarı da zaman içerisi azalacak ve “ısı ölümü” yaşanacağı ve bunun bir sonucu olarak da fiziksel anlamda hiçbir iş yapılamayacak ve dünya üzerindeki hayatın sona ereceği de söylenenler arasındadır. Bir yandan da sürekli genişleyen bir evrenin içinde olduğumuzu düşünecek olursak ısıl dengeye hiçbir zaman ulaşılamayacak ve bu “ısı ölümü” kuramı çürütmeye yetecektir.
Kainatın şu anki durumunu göz önüne alacak olursak, öne çıkan fikirlerden biri kainat bize muhtemelen evrendeki bütün enerji kaynaklarının yok olacağı yıldızların bile söneceği bir gelecek sunacaktır. Bununla beraber, belki de küçük parçacıklardan oluşan sistemlerden az miktarda da olsa enerji üretmek mümkün olur ve son derece düşük enerji seviyelerinde de olsa ‘ilginç olaylar yaşanmaya devam edebilir.’
Kaynakça
- ^ Carnot, S. (1824/1986).
- ^ (1980), Chapter 5.
- ^ Adkins, C.J. (1968/1983), s. 56-58.
- ^ Münster, A. (1970), s. 11.
- ^ Kondepudi, D., Prigogine, I. (1998), s.67-75.
- ^ Lebon, G., Jou, D., Casas-Vázquez, J. (2008), s. 10.
- ^ Eu, B.C. (2002), s. 32-35.
- ^ Clausius, R. (1850).
- ^ Clausius, R. (1867).
- ^ Thomson, W. (1851).
- ^ a b Münster, A. (1970), s. 45.
- ^ a b Lieb, E.H., Yngvason, J. (1999), s. 49.
- ^ , Muncaster, R.G. (1980). Fundamentals of Maxwell's Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics, Academic Press, New York, ISBN0-12-701350-4, s. 15.
- ^ Planck, M. (1926), s. 457, Vikipedi editörünün çevirisi.
- ^ (1909).
- ^ Buchdahl, H.A. (1966), p. 68.
- ^ Sychev, V. V. (1991). The Differential Equations of Thermodynamics. Taylor & Francis. ISBN . Erişim tarihi: 26 Kasım 2012.
- ^ Planck, M. (1926).
- ^ Buchdahl, H.A. (1966), s. 69.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Termodinamigin Isildevinimin ikinci yasasi izole sistemlerin entropisinin asla azalamayacagini belirtir Bunun sebebini izole sistemlerin termodinamik dengeden maksimum entropi asamasi spontane olarak olusmasiyla aciklar Buna benzer olarak surekli calisan makinelerin ikinci kanunu imkansizdir Termodinamigin ikinci yasasi deneysel olarak bir isi bilgisi onermesi olarak kabul edilir fakat bu yasa altinda yatan istatistiksel kuantum mekanigiyle anlasilabilir ve aciklanabilir Istatiksel mekanik literaturunde entropi makroskopik evrelerde mikroskobik gruplasmalarin olcumu olarak ifade edilir Cunku isibilgisinin denge dengede olmayan duruma gore buyuk miktarda mikroskopik dizilise sahiptir Bu maksimum entropiye sahiptir ve ikinci yasayi takip eder cunku duzensiz yalniz degisim kismen sistemin isi bilgisinin dengesini gelistirmesini saglar Zamana bagli bir ifade olarak sicaklik basinc ve kimyasal potansiyel isibilgisi dengeye dogru izole edilmis ve yercekiminin onemsiz oldugu sistemde azalir Ikinci yasa farkli bircok sekilde aciklanabilir ama ilk formulasyon 1824 yilinda Fransiz bilim insani Sadi Carnot tarafindan yazilmistir Ikinci yasanin ilk ifadeleri yalnizca yatay duzlemde yercekimisiz alanda dogrudur Ikinci yasa ic enerji U ya esit olarak kapsamli ozelliklerin fonksiyonu olarak yazilabilir Kutle hacim entropi TanimiTermodinamigin birinci yasasi termodinamik enerjinin ic enerji olarak da bilir butun isibilgisi sistemler bilinmeyen klasik mekanikler haric basit tanimini ve dogadaki enerji korunumunu saglar Birinci yasadaki enerji konsepti dogal surecteki gozlemleri hesaplayamaz Ornegin isi her zaman istemsizce yuksek sicakliktan dusuk sicakliga dogru akar disaridan is yapilmadigi surece Birinci yasa baslangic ve son durumlardaki degisimin simetrik oldugunu aciklar Bunun aciklanmasindaki anahtar durum termodinamigin ikinci yasasi boyunca yeni fiziksel ozelligin tanimi entropidir Tersine cevrilebilir durumda entropideki sonsuz kucuk artis dS isi transferindeki sonsuz kucuk degisimin dQ kapali sistemdeki sicakliga T bolumumden elde edilebilir dS dQT displaystyle dS frac delta Q T Korunumlu entropi sistemindeki ic isibilgisi denge zamana bagli degildir Korunumlu sistem birbirinden ayrilmis baslangic sistemlerden olusur ama hepsi kendi dengesine sahiptir Parcaciklar tekrar hareket ettirilirse onceki sistemler genel bir etkilesim icinde olacaktir ve kendi yeni son isibilgisi sistemini olusturacaktir Baslangic entropiler son entroplerden azdir Eger baslangic entropilerinin hepsi ayni degerdeyse baslangic ve son entropileride ayni olacaktir Vucuttaki temel denge baskasiyla kesinlikle bircok emprik sicaklik olcusu vardir isibilgisi sistemin arasindaki temel denge esit derecelerde sonlanir Isibilgisinin baslangic yasasi kisa durumlarda iki ortamin ayni derecelerde recogne etmesine izin verir Ikinci kural unlu bir sicaklik olcegine izin verir Bu olcek kesin isibilgisi sicaklik ve herhangi bir ozel bagimsiz isibilgisi sistemin ozelliklerini tanimlar Isibilgisinin 2 Kurali bircok ozgul yolla aciklanabilir Bunlarin en onemlilerin durumu Rudolph Clasius 1854 Lord Kelvin 1851 ve Constantin Caratheodory 1909 tarafindan aciklanmistir Bu ifadeler kesin sureclerin olanaksizligi ilkesine dayanarak genel fizik terimlerine dayanir Clasius un ve Kelvin in aciklamalari esdeger olarak kabul edilir Carnot s prensibiIsibilgisinin 2 Yasasinin tarihsel kokeni dir Bu prensibi Carnot makinesi dongusunu gosterir Carnot makinesi isi ve is aktarimlarinin birbiri icinde surekli kendi ic isibilgisi dengede almasini duzenler Bu makine isi makinelerinin verimliligiyle ilgilenen muhendislerin ilgisini ceker idealize edilmis bir aygittir Carnot s prensibi kalasik teorisi caddice anlasildiktan sonra ve termodinamigin 1 Kanununun ve entropinin matematiksel izahindan once tanitilmistir 1 Kanunun yorumlanmasi Termodinamigin 2 Kuralinin anlasilmasini kolaylasmistir Bu bugun icin bile hala gecerlidir Quasi statik veya tersinir Carnot dongusunun verimliligi sadece iki isi kaynaginin sicakligina ve calisan kaynagin serbestligine baglidir Bir Carnot makinesi bu iki sicakligin kullanilmasiyla en verimli sekilde kullanilabilir Clausius ifadesiAlman bilim insani isi ve is aktarimlarini inceleyerek isibilgisinin 2 Yasasini kurmus oldu 1850 onun bu yasayi aciklamasi Clausius ifadesi olarak bilinir 1854 Almanya Isi hicbir zaman soguk bir cisimden ilik bir cisme bir takim degisiklikler olmadan gecmez Isi sicak bolgelerden soguk bolgelere aniden ve is yapmadan gecemez Bu siradan bir donma olayiyla kanitlanabilir Bir dondurucu icinde isi soguktan sicaga ve sadece disaridan bir kuvvet uygulandiginda gecebilir Kelvin ifadesiLord Kelvin 2 kanunu su sekilde ifade etmistir Donuk meteryal araciligiyla etrafindaki en soguk nesne vasitasiyla sogutulmus herhangi bir maddeyi turetmek imkansizdir Planck prensibi1926 da Max Planck termodinamik temelleri hakkinda onemli bir makale yazdi Bu makaleyle kapali sistemlerdeki ic enerjinin bir isochosic adiabatic surecle arttigini gosterdi dd Bu formulasyon isi ve sicakliktan ya da entropiden bahsetmedi ve dolayli olarak bu kavramlara bagli degildi fakat 2 Kanunun icerigini tasiyordu Bagli oldugu ifade surtunme kuvveti asla pozitif is yapamaz di Planck kelimelerin eski bicimlerini kullanarak sunu yazdi Isinin surtunme tarafindan uretimi tersinir degildir Caratheodory prensibi isibilgisi saf matemetic aksiyemura bagli olarak formule etti Onun 2 Kanunla ilgili ifadesi Caratheodory prensibi olarak bilinir Caratheodory adyabatik erisebilirlik kavramini ilk kez tanimladi ve klasik isibilgisinin alt kategorilerini siniflandirdi Bunlar geometric isibilgisi olarak adlandirilir ve enerjinin quasi statik olarak transferinin miktari prensibini taktik Eder Cunku isi holonomic bir surectir dQ TdS displaystyle delta Q TdS Caretheodory nin Prensibi 2 Kanunu ifade Eder ve Clausius ya da Kelvin Planck ifadesine esdegerdir 2 Kanunun tumicerigini almak icin Caratheodory Prensibi Planck Prensibi ne ihtiyac duyar Isokharic is her zaman basta kendi is isibilgisi denkligine sahip kapali sistemin ic enerjisini artirir Clausius ve Kelvin ifadelerinin esitligi Clausius bildirimi nin Kelvin bildirimi turetimi Bir motorun Kelvin ifadesiyle calistigini dusunelim Mesela biri isiyi tuketiyor ve bunu butunuyle bir is e dounusturuyor Bu yeni yapilmis makinenin net ve biricik etkisi iki motor icerir Aktarilmis isi DQ Q 1h 1 displaystyle Delta Q Q left frac 1 eta 1 right Sonuc olarak Kelvin ifadesinin aykiriligi Clausius ifadesinin aykilirligi anlamina da gelir yeni Clausius ifadesi Kelvin ifadesini de ima eder Bunu ayri sekilde Kelvin ifadesi Clausius ifadesini ima Eder sekilde de bulabiliriz Bu yuzden bu iki ifade esdegerdir Yercekimi sistemleriYercekimsiz sistemlerde nesne her zaman pozitif isi kapasitesine sahiptir bu da sicakligin enerji ile yukselecegi anlamina gelir Bu yuzden enerji yuksek sicakliktaki nesneden dusuk sicakliktaki nesneye gectiginde kaynak sicaklik duser Buna ragmen lavabo sicakligi yukselir Sonuc olarak sicaklik farkliliklari zamanla azalma egilimindedir Ancak bu yercekimi kuvvetinin onemli oldugu sistemlerde her zaman gecerli olan bir durum degildir Kara delikler en goze carpan orneklerdir ve teoriye gore kara delikler negatif isi kapasitesine sahiptirler Kara deliklerin buyuklukleri arttikca sahip olduklari enerji de artar ama sicakliklari duser Sonuc olarak samanyolundaki super buyuk kara deligin sicakligi 10 4K varsayilir bu sicaklik kozmik mikrodalga arka plan sicakligi olan 2 7 K den cok dusuktur fakat bu kara deligin dusuk olan sicakligi daha cok azalir cunku kozmik mikrodalga arka plan fotonlarini absorbe ettigin icin kutlesi artar Bu yuzden yercekiminin oldugu ortamlarda kutle ve enerji esit olarak dagilmaz SonuclarSurekli hareket yasasiIkinci yasanin olusturulmasindan once surekli hareketli makinelerinin icadiyla ilgilenen pek cok insan makinenin gucu ile sistemin buyuk ic enerjisinin farkini alarak isibilgisinin birinci yasasinin kisitlamalarindan kacinmaya calismislardir Bu tur makinelere devridaim makinesi denir Ikinci kanun bu makinelerin imkansizliklarini aciklamistir Carnot kuramiCarnot teoremi 1824 her makineyi maksimum verimlilikle sinirlandirir Verimlilik yalnizca sicak ve soguk termal rezervuarlar arasindaki sicaklik farkina baglidir Carnot kurami asagidaki ifadelere dayanmaktadir Iki isi rezevuari arasindaki tek yonlu butun isi motorlari ayni iki rezervuar arasindaki bir Carnot motorundan daha az verimlidirler Iki isi rezervuari arasindaki tek yonlu butun isi motorlari ayni iki rezervuar arasindaki bir Carnot motoruyla esit verimliliktedirler Carnot un ideal modelinde kalorik isi tersinir hareket dongusunu eski haline ceviren ise donusturusur Ancak Carnot mekanik ise donusmeyen isi kayiplarinin oldugunu varsaymistir Sonuc olarak Carnot dongusunun cevrilebilme ozelligini gerceklestiren gercek isi makinesi yoktur ve bu makine cok verimsizdir Clausius esitsizligiClausisus teoremi 1854 dongu surecine dayanir dQT 0 displaystyle oint frac delta Q T leq 0 Esitlik tersinir durumu gosterir ve lt isareti tersinemez durumlarda yer alir Tersinir durum entropi hal fonksiyonunu aciklamak icin kullanilir Cunku dongusel islemlerde hal fonksiyonunun degisimi sifirdir Termodinamik sicaklikHerhangi bir isi motoru icin verimlilik h AqH qH qCqH 1 qCqH 1 displaystyle eta frac A q H frac q H q C q H 1 frac q C q H qquad 1 A birim dongude yapilan is Carnot onermesi tersinir ayni iki isi rezervuarlarini calistiran tersinir makinelerin esit verimlilikte oldugunu ifade eder Sonucta T1 ve T2 sicakliklarinda calisan herhangi tersinir isi makinesi bu sicakliklarda ayni verimlilikte olmak zorundadir Bu yuzden verim sicakliga bagli fonksiyondur qCqH f TH TC 2 displaystyle frac q C q H f T H T C qquad 2 Ayrica T1 ve T3 sicakliklarinda calisan tersinir bir isi makinesinin T1 ve ara sicaklik olan T2 arasindaki verimliligiyle T2 ve T3 arasindaki verimliligi esit olmak zorundadir f T1 T3 q3q1 q2q3q1q2 f T1 T2 f T2 T3 displaystyle f T 1 T 3 frac q 3 q 1 frac q 2 q 3 q 1 q 2 f T 1 T 2 f T 2 T 3 Suyun uc sicaklik noktalarindan T1 displaystyle T 1 sabit referans sicaklik olarak dusunulurse f T2 T3 f T1 T3 f T1 T2 273 16 f T1 T3 273 16 f T1 T2 displaystyle f T 2 T 3 frac f T 1 T 3 f T 1 T 2 frac 273 16 cdot f T 1 T 3 273 16 cdot f T 1 T 2 Sonucta isibilgisi sicaklik T 273 16 f T1 T displaystyle T 273 16 cdot f T 1 T f fonksiyonu isibilgisi sicaklik fonksiyonu varsayilir f T2 T3 T3T2 displaystyle f T 2 T 3 frac T 3 T 2 Ve referans sicaklik T1 in degeri 273 16 olur Herhangi referans sicakligi ve diger pozitif sayisal degerler Kelvin cinsinden olmalidir EntropiClausius a gore asagidaki esitlik tersine de esitlenebilir dQT 0 displaystyle oint frac delta Q T 0 Bu demektir ki LdQT displaystyle int L frac delta Q T cizgi integrali bagimsiz yoldur Boylece durum foksiyonu olan entropy asagidaki gibi tanimlayabiliriz dS dQT displaystyle dS frac delta Q T Bununla birlikte yukardaki formulun integralini alarak sadece entropy nin farkini elde edebiliriz Mutlak degeri elde etmek icin muhtesem kristalle icinmutlak sifirda s 0 olan isibilgisinin 3 Yasasina ihtiyacimiz vardir Herhangi cevrilemeyen surecte entropy bir durum foksiyonu oldugu icin gercek olmayan cevrilebilen surecte birlikte baslangic ve terminal durumlari arasinda baglanti kurabiliriz Simdi cevrilebilen sureci cevir denilen cevrilemeyen surecte kombin et ve Clausius esitsizligine basvur DS dQT dQT lt 0 displaystyle Delta S int frac delta Q T oint frac delta Q T lt 0 BoyleceDS dQT displaystyle Delta S geq int frac delta Q T Esitlik donusumun cevrilebildigi yerlerde olur Eger surec isisiz bir surecse dQ 0 displaystyle delta Q 0 bu yuzden DS 0 displaystyle Delta S geq 0 Ekserji mevcut kullanilabilir isOnemli ve ideallestirilmis ozel durum ikinci yasa olan isale edlimis sisteme tum sistem veya evrensel basvurulmak icindir Bu islem iki parttan olusur Bunlar ilgilenilen alt sistem ve cevresel alt sistemdir Bu cevresel limitsiz sicaklik haznesi olarak dusunulebilir TR sicakligi ve PR basinci altinda Ayrica ne Kadar isi transefer olsa da sub systeme sicaklik her zaman TR kalir ayrica hacim ne kadar degissede PR de her zaman sabit kalir Ne degisiklik olursa olsun dS ve dSR de ikici yasaya gore Stot olan isole total sistem azalmamaktadir dStot dS dSR 0 displaystyle dS mathrm tot dS dS R geq 0 Termodinamigin ilk yasasina gore dU degisimi alt sistemin ic enerjisinde esittir su systeme eklenilen toplam isi dq eksi alt sistem tarafindan yapilan herhangi is dw ve arti alt sisteme giren herhangi net kimyasal enerji d miRNi yani dU dq dw d miRNi displaystyle dU delta q delta w d sum mu iR N i miR kimyasal turlerin kimyasal potansiyelleri discevrede simdi rezervuari terk eden isinin alt sisteme girisi dq TR dSR TRdS displaystyle delta q T R dS R leq T R dS Herhangi alt sistem tarafindan net is dw uymalidir ki dw dU TRdS miRdNi displaystyle delta w leq dU T R dS sum mu iR dN i Bu kullanislidir ayirmak icin alt sistem tarafindan yapilan isi dw ve alt sistem tarafindan yapilan isi dwu ve alt sistem tarafindan yapilan pR dV genisler dis cervre basincina karsi Asagida verilen iliski kullanisli is icin verilmistir dwu d U TRS pRV miRNi displaystyle delta w u leq d U T R S p R V sum mu iR N i isibilgisi potansiyelin tam turevini tanimlamak icin alt sistemin mevcut veya exergy E si demek uygundur E U TRS pRV miRNi displaystyle E U T R S p R V sum mu iR N i Bu yuzden ikinci yasa ima eder herhangi subsystemine ve limitsiz sicaklik ve basincina ayrilmis surec icin dE dwu 0 displaystyle dE delta w u leq 0 Ikinci yasa tahmin eder E deki azalisi degismeyen ve degisen surecler icin dStot 0 displaystyle dS tot geq 0 Esdeger oldugunda dE dwu 0 displaystyle dE delta w u leq 0 Bu aciklama 2 yasayi faydali hale getirmek icin desing motor calismasina makroskopic degerlere izin verir Bu degisiklikler referans durumuyla dengeye ulasan durumlar altindaki sistemler tarafindan tahmin edelir Bakinci2 yasa etkisi bu yaklaisim 2 yasanin muhendislik pratiklerinde cevre hesaplarinda ekoloji sistemlerinde ve obur hesaplarda yarar saglar TarihceIsinin mekanik ise donusumuyle ilgili ilk teori Nicolas Leonard Sadi Carnot tarafindan 1824 yilinda ortaya atildi Carnot ilk kez bu donusumun verimliliginin makine ile cevresi arasindaki sicaklik farkina bagli oldugunu fark etti Rudolf Clausius Prescott Joule in enerjinin korunumu hakkindaki calismalarini da goz onunde bulundurarak 1850 yilinda ikinci kanunu formulize etti Bu kanuna gore bugun bilinenin aksine isi kendiliginden soguktan sicaga dogru akmazdi Buradan hareketle Rudolf entropinin tanimini ve Sadi Carnot un ilkelerini tanimlayabildi 19 Yuzyilda yayimlanan Kelvin Planck in aciklamasi soyleydi Hicbir cihaz tek basina bir rezervuardan isi alarak periyodik olarak calisamaz ve is elde edemez Bu aciklama Clausius un aciklamasiyla esdegerdi Boltzmann in yaklasimi icin ergodik hipotez de oldukca onemliydi Bu hipotez soyle soyluyordu Kucuk alanlardaki bolgelerin evrelerinin gerceklesmesi icin gereken zaman bu bolgenin hacmiyle dogru orantilidir Ayni zamanda ortalama zaman ve statistik gruplarin ortalamasi da estir Sadece klasik sistemlerde degil quantum mekaniginde de entropiyi maksimuma cikarma egilimi oldugunu gorebiliriz Bu yuzden ikinci kanunda verilen ilk kosullar dusuk entropiyle verilir Sonuclar ust sinif izole edilmis quantum sistemleri icin gecerli olur Ornegin konteynr icindeki gaz Butun sistemde hic entropi olmasa ve sistem saf olsa bile gaz ve konteynir arasindaki karmasiklik gazin yerel entropisindeki artisi verir Bu sonuc quantum isibilgisinin en onemli sonucudur Bugun evrenin ilk zamanlarinda neden dusuk entropiye sahip oldugunu anlamak icin oldukca caba harcaniyor Yasal olarak gecersiz aciklamaIkinci kanun birkac maddeyle ozetlenebilir Tek basina bir rezervuar kullanarak periyodik bir is elde etmek imkansizdir Kelvin 1851 Isiyi motor kullanarak sicakligin az oldugu yerden cok oldugu yere aktarmak imkansizdir Clausius 1854 K Eger isibilgisi is icin sonlu bir oran kullaniliyorsa sonsuz bir enerji kullanilmistir Matematiksel aciklama Rudolf Clausius 1856 yilinda Rudolf Clausius isinin mekanik kuraminin ikinci ana onermesi adini verdigi kuramini su sekilde acikladi dQT N displaystyle int frac delta Q T N Q isi T sicaklik ve N karsiligi verilmemis donusumlerin esdegeri 1865 de Clausius bu esdegeri entropi olarak tanimladi Clausius sonucta su yargiya vardi Evrenin entropisi maximum olma egilimindedir Bu onerme ikinci kanunun en bilinen kismidir Bu tanim cok basit durabilir ancak tabii ki kompleks bir tanimin sadelestirilmis halidir Zaman varyasyonu acisindan ikinci kanunun matematiksel ifadesi dSdt 0 displaystyle frac dS dt geq 0 S Sistemin entropisi T zaman Bu esitlik geri donusebilen surecler icin kullanilir Eger surec geri donemezse gt isaret alir Izole edilmis sistemler icin ikinci kanunun alternatif bir formulu vardir dSdt S i displaystyle frac dS dt dot S i eger S i 0 displaystyle dot S i geq 0 ise S i displaystyle dot S i entropi oranlarinin toplami Bu formulun avantaji entropi uretiminin etkilerini gostermesidir Entropi uretimi orani makinelerin etkisi acisindan cok onemlidir Ikinci kanunun kapali sistemler icin formulu dSdt Q T S i displaystyle frac dS dt frac dot Q T dot S i Eger S i 0 displaystyle dot S i geq 0 ise Q sisteme akan isi T displaystyle T Isinin sisteme girdigi noktadaki sicaklik Eger sisteme belirli noktalardan isi verilirse bu degerlerin toplaminin alinmasi gerekir Acik sistemler icin denklem bilesen degisim imkani var dSdt Q T S S i displaystyle frac dS dt frac dot Q T dot S dot S i Ancak S i 0 displaystyle dot S i geq 0 Buradaki S displaystyle dot S sisteme giren madde miktariyla dogru orantili olarak sisteme giren ancak kullanilmayan enerji miktarini entropi simgeler Bu kullanilmayan enerjinin zamana gore tureviyle karistirilmamalidir Eger gereken yerlere istenen miktarda madde saglanirsa bunlarin katkilarini hesaba katmak adina hepsinin toplami alinir Istatistiksel mekanikte ikinci yasa icin verilen aciklamada maddenin atom ve molekullerden olustugunu ve bunlarin da sabit bir yorungede hareket halinde oldugu varsayimini kabul ederiz Belirli durumlarda ve hizlarda sistemdeki her bir parcacik icin verilen durumun adi sistemdeki microstate anlik durum olarak adlandirilir ve sabit hareketten dolayi sistem kendi microstate ini surekli yeniliyor Istatistiksel mekanigin bir baska varsayimi ise dengede olan sistemlerde her bir microstate in olusma ihtimali birbirine esit olur ve bu varsayimdan yola cikilacak olunursa ikinci yasanin mutlaka istatistiksel bir goruse de sahip olmasi gerektigi kanisina varilabilir N nin sistemdeki parcacik sayisi oldugunu dusunursek istatistiksel degisim miktarini da 1 N ile hesaplayabiliriz Gunluk hayatta ciplak gozle gorebildigimiz olaylari dusundugumuzde ikinci yasanin islev disi kalma ihtimali sifir Ancak az miktarda parcacigi olan sistemler icin isibilgisi kat sayilar entropi dahil ikinci yasanin kuramda ongordugu rakamlara gore ciddi bir sapma gosterebilir Isibilgisi kurami istatistikler varyasyonlarla ilgilenmez Istatistiksel mekanigin kokeniLoschmidt paradoksuna ragmen ikinci yasanin kokeninin gecmise dair bazi varsayimlara sahip olmasi gerekmektedir Tabi sistemin gecmiste bazi durumlarda bagimsiz hareket ettigi de olmustur Bu durum basit bir olasilik hesabiyla hareket etmemize imkan saglar Bu durum limit durumu olarak da bilinir ve ikinci yasa eninde sonunda baslangic degerinin neticesinde ortaya cikmistir hatta muhtemelen evrenin olusmasi ile sonuclanan buyuk patlamanin bile basinda Verilen varsayimlardan yola cikildiginda istatistiksel mekanikte bahsedilen ikinci yasa tam anlamiyla dogru varsayilmamaktadir Bunun yerine temel bir kavramin sonucu olarak kabul edilir Ikinci yasanin ilk kisminda bahsedilen isica yalitilmis sistemlerin entropisi sadece oncelikli denk olasiligin goz ardi edilebilecek bir kismini artirir varsayimi ancak isil denge halindeki bir sistemi kisitladigimizda ortaya cikar Isil dengedeki izole bir sistemin entropisinin depoladigi enerji miktarini E displaystyle E ile gosterecek olursak S kBln W E displaystyle S k mathrm B ln left Omega left E right right W E displaystyle Omega left E right IleE displaystyle E E dE displaystyle E delta E arasindaki kisa araliktaki kuantum durumlarinin sayisidir dE displaystyle delta E Ise gozle gorulur derecede fakat kucuk bir miktar enerji araligini simgeler Kesin bir dille konusmak gerekirse entropimiz sectigimiz dE displaystyle delta E degerine bagli olarak degisim gosterir Yalniz isibilgisi limiti dusundugumuzde sistemin ulasabilecegi maksimum genislik sectigimiz belirli bir entropi hacmi ve kutlesi belirli dE displaystyle delta E degerinden etkilenmez Farz edelim ki boyutu belirli bir sayida degiskenle sabit tutulmus izole bir sistemimiz var Bu degiskenler sistemin hacmini kutlesini ya da pistonlarin konumunu belirliyor olabilir W displaystyle Omega Degeri sistemdeki bahsettigimiz degiskenlere bagli olacaktir Eger bir degisken sabitlenmemisse pistonun ulasacagi en yuksek nokta gibi sistemdeki dengeden dolayi bagimsiz degiskene etki yapacak olan W displaystyle Omega degeri degiskeni olabilecek en muhtemel degerde sabitleyecektir Eger degisken baslangictan itibaren sabit bir degere sahipse ve yeni dengeye an itibariyla ulasilmissa W displaystyle Omega degerini maksimuma ulastirmak icin degisken kendini ayarlayacaktir Denge halinde degilken sistemin entropisi S kB jPjln Pj displaystyle S k mathrm B sum j P j ln left P j right Isil dengede ic enerji araligi Pj displaystyle P j olan durumlarin olusma olasiligi1 W displaystyle 1 Omega Eger boyle bir durum olursa S nin tanimi da onceki isil denge durumunda kullanilan acilim ile aynidir Denge durumunda basladiktan bir sure sonra degisken sayisindaki sinirlamayi kaldirdigimizi varsayalim Bundan hemen sonra da sisteme W displaystyle Omega kadar microstate yapi olusturma ekledigimizde ve sistem hala denge durumuna ulasmadiginda sistemin calisabilir durumda olma ihtimali1 W displaystyle 1 Omega Daha once en son denge halinde gordugumuz gibi entropi ya onceki denge durumunda kalacak ya da oncekine nazaran ufak bir artis gosterecektir Geri Donusturulebilir Islemler icin Entropideki Degisim Ikinci yasanin ikinci bolumunde de belirtildigi uzere geri donusumu mumkun olan yontemlerdeki entropi degisimi sekildeki gibidir dS dQT displaystyle dS frac delta Q T Bu durumda sicaklik ise 1kBT b dln W E dE displaystyle frac 1 k mathrm B T equiv beta equiv frac d ln left Omega left E right right dE Sistemde rolu olan bazi dis degiskenler de mevcut Genel olarak bunlarin sistemi degistirme imkani var cunku enerji disaridan saglanir ve sistem icin her sey demektir Kuantum mekaniginin isi degisimsiz kuramina gore neredeyse hic degismeyen bir sistemin durumunun limitini aldigimizda sistemin enerji ozunde bir degisim olmaz Genel haliyle kuvvet X dis etkenleri ayarlayan degisken ise x olarak gosterildiginde Xdx displaystyle Xdx tabiri sistem tarafindan yapilan saf isi verir Buradaki degisim ise dx ile gosterilir Mesela x e hacim X e de basinc dememiz gibi Sistemdeki enerji miktari Er displaystyle E r ise X dErdx displaystyle X frac dE r dx dE displaystyle delta E Genisligi boyunca sistem herhangi bir enerji durumunda olabilecegi icin sistemdeki genel kuvveti tahmini degerler icinde yazacak olursak X dErdx displaystyle X left langle frac dE r dx right rangle Ortalama degeri degerlendirecek olursak W E displaystyle Omega left E right degerini parcalara ayiriyoruz Bunun nedeni olarak da Y displaystyle Y ve Y dY displaystyle Y delta Y araligi icinde dErdx displaystyle frac dE r dx degere karsilik gelecek kac tane deger oldugunu kontrol ediyoruz Karsimiza cikan degere de WY E displaystyle Omega Y left E right diyoruz Sonuc olarak elimizde W E YWY E displaystyle Omega left E right sum Y Omega Y left E right Ortalama gucu genellemek adina da soyle yazabiliriz X 1W E YYWY E displaystyle X frac 1 Omega left E right sum Y Y Omega Y left E right Bu acilimi entropinin tureviyle bagdaslastirabiliriz Denklemde x i x dx diye degistirdigimizi varsayalim Bu durumda W E displaystyle Omega left E right degeri de etkilenir x e bagli oldugundan ve de E displaystyle E ile E dE displaystyle E delta E arasindaki degerleri alabilir NY E WY E dEYdx displaystyle N Y left E right frac Omega Y left E right delta E Ydx Yukaridaki denklem ele alindiginda eger Ydx dE displaystyle Ydx leq delta E durumu saglandiginda butun enerji degerleri E displaystyle E ile E dE displaystyle E delta E degerleri arasinda yerini alir ve W displaystyle Omega degerinin artisina yardimci olurlar Sistemlerin baslangic enerjilerinin toplami asagi yukari NY E dE displaystyle N Y left E delta E right olur ve aralarindaki fark da NY E NY E dE displaystyle N Y left E right N Y left E delta E right ile ifade edilir Elde edilen sonuc ise W displaystyle Omega degerine yapilan net katkiyi gosterir Eger E dE displaystyle E delta E degerden daha yuksekse E ile E dE displaystyle E delta E arasinda bir degere sahip enerji aciga cikacaktir NY E displaystyle N Y left E right ve NY E dE displaystyle N Y left E delta E right toplamlarda da sayilan enerji degerleri ozetlenecek olursa su sekilde gosterilebilir W x E YY WY E x WX E x displaystyle left frac partial Omega partial x right E sum Y Y left frac partial Omega Y partial E right x left frac partial left Omega X right partial E right x W displaystyle Omega degerinin logaritmik turevi ise ln W x E bX X E x displaystyle left frac partial ln left Omega right partial x right E beta X left frac partial X partial E right x Ilk terim bazi durumlarda sinirlari asabilecegi icin alternatif olarak kullanabilecegimiz S x E XT displaystyle left frac partial S partial x right E frac X T Ve S E x 1T displaystyle left frac partial S partial E right x frac 1 T Bu ikisini bir araya getirmeye calistigimizda ise elimize gecen denklem dS S E xdE S x Edx dET XTdx dQT displaystyle dS left frac partial S partial E right x dE left frac partial S partial x right E dx frac dE T frac X T dx frac delta Q T Kanonik set ile ifade edilen sistemlerin turevleriSisteme giren ya da sistemden cikan herhangi bir isi var ise denge halinde bu isiyi T ile gosterip bu isinin sistemdeki belirli yerlere dagilma olasiliginin Kanonik Set ile bulunusu Pj exp EjkBT Z displaystyle P j frac exp left frac E j k mathrm B T right Z Temel olasilik hesabindan bilindigi uzere bagimsiz bir olayda meydana gelmesi ihtimal dahilinde olan olaylarin olasiliklari toplami 1 etmelidir Bizim denklemimizde de Z degerlerin toplaminin 1de bulusmasini saglayan temel faktordur Bu tarz fonksiyonlara da ayrilma fonksiyonu denir Dis etkenlere bagimli isinin degisimi ve bunun enerji seviyesine olan katkisini gosteren genel formul S kB jPjln Pj displaystyle S k mathrm B sum j P j ln left P j right Bu denklemden dS kB jln Pj dPj displaystyle dS k mathrm B sum j ln left P j right dP j Pj displaystyle P j degerini elde ettigimizde elimizde kalan son deger dS 1T jEjdPj 1T jd EjPj 1T jPjdEj dE dWT dQT displaystyle dS frac 1 T sum j E j dP j frac 1 T sum j d left E j P j right frac 1 T sum j P j dE j frac dE delta W T frac delta Q T Kuantum mekaniginin birlestiriciligiKuantum mekaniginin temel yapitaslarindan biri olan ikinci yasaya baktigimizda gecis olasilik matrisi ve zamanla gelisen bir birim var Ikinci yasanin bu denli genis kapsamli olmasi onu bir bakima diger onerme ve yasalarin birlestiricisi de yapar Genellenebilirligi ve birlestiriciligi acisindan herhangi bir ileri kanita veya destege ihtiyacinin olmamasi evrensel genelgecer bir une ve guvene sahip olmasinin da bir nevi kanitidir Dengede olmayan durumlarTermodinamik analiz amaciyla yaklastigimizda aslinda uzay zaman cizgisinden rastgele secilmis herhangi bir olayin isibilgisi dengede oldugu dusunulur Daha genis bir perspektiften bakildiginda ise uzay zaman cizgisinde bulunan kisacasi evrendeki hicbir sey tam anlamiyla isibilgisi denge halinde degildir hic de olmamistir Bir diger ayrinti ise termal dengedeki bir sistemin istatistiksel olarak denge durumundan ciktigi anlar olmasi dogaldir Bazi karsilasmasi guc olaylarda ise sicak parcaciklarin soguk parcaciklardan enerji caldigi ve bu sayede ortamdaki sicak kismin daha sicak soguk kismin ise giderek daha soguk bir hal aldigi gozukmustur son derece kisa bir zaman araliginda olsa bile Fizigin dahil oldugu ve gerceklesmesi kagit uzerinde mumkun olan bazi olaylar vardir ki bilindik isibilgisinin denge kurallarinin cok otesinde davranis sergileyen Dalgalanma onermesi ise bir sistemin dengeden uzak kaldigi sure zarfi boyunca entropisindeki degisim miktarinin olasiliginin rakamsal olarak yaklasik bir degerini verir Gecmisten buguneIsibilgisinin ikinci yasasi bir fizik yasasidir ve geri donuslu zaman kavramini kapsamaz Aslinda gecmiste bu yasanin gelistirilmesi acisindan zamanda ileri ve geri gidildiginde ne gibi farkliliklar olabilecegine dair bir aciklama eklenilmesi gerektigi onerilse de gunumuze kadar pek bir degisim sergilememistir IhtilaflarMaxwell in IblisiJames Clerk Maxwell A ve B seklinde ikiye bolunmus bir konteynir hayal etmistir Iki parca da esit miktarda ve esit sicakliktaki ayni gazla doldurulmus ve yan yana bekletilmektedirler Iki taraftaki molekulleri de izlerken hayali iblisin iki tarafta da savunma yaptigini gorur A daki iblis daha hizli hareket ettiginde B ye ucan molekuller olur ve A yavasladigindan B zaman icinde daha fazla isinir ve A daki isi duser Bu isibilgisinin ikinci yasasina gore tamamen zit bir durumdur Loschmidt paradoksuLoschmidt paradoksu geri dondurulme paradoksu olarak da bilinir Zamanla simetrik dinamiklerin geri dondurulebilen isleme bir faydasi olma ihtimalinin dusunulmesine karsi cikilmaktadir Bu bizi ciplak gozle isleyisini gorebildigimiz sistemlerin davranislarini aciklamak adina isibilgisinin ikinci yasasini kullanmak icin bilinen butun yontemlerden bir adim daha one goturmektedir Bu yontemlerin neredeyse hepsi kuramdan gucunu almakla beraber bazilari kendi aralarinda celismektedir Bu yuzdendir ki onlara paradoks deniyor Gibbs paradoksuIstatistiksel mekanikte birbirinden ayrilabilen parcaciklardan olusan ideal gazin entropisinin basit bir turevini aldigimizda bunun isibilgisinin ikinci yasasinin bazi kurallarini cignemesinin yani sira kanonik sete dayanmasi ise bizi bu paradoksun Gibbs paradoksu olarak adlandirmaya itmektedir Parcacik turunun entropiyi direkt olarak etkilemedigi fark edildiginde bu paradoks durdurulmustur Bilindik bir tabir ile bu kuantum mekanigi ile bagdastirilan ve parcaciklarin birbirinden farksizligi ile aciklanan bir tanimlamadir Yineleme teoremiYineleme kurami der ki belirli sistemler uzerlerinden yeteri miktarda uzun bir zaman gectiginde baslangic durumlarina son derece yakin bir konuma gelirler Bu yenileme zamani yenilenene kadar akip giden zaman exp S k displaystyle sim exp left S k right tabirle bulunmaktadir Bu formul enerjinin korundugu butun fiziksel sistemlere uygulanabilir Yineleme kurami belli ki isibilgisinin ikinci yasasiyla bir celiski icindedir Ikinci yasa der ki bir sistem cogu durumda oyle yuksek enerji seviyelerine gelir ki geri donusu mumkun olmayan kazanclar veya kayiplar yasanir ve sistem bir daha asla eski haline donemez Bu paradoksu cozume kavusturmanin birden cok yolu var ancak hicbiri evrensel olarak kabul gormemistir Bunlardan bir tanesi yinelenme icin gereken zaman o kadar buyuktur ki ne kadar uzun zaman gecerse gecsin sistemin baslangic haline yaklasmasi bile gozlenememektedir Kainatin gelecegiGecmisten gelen bir uyari olarak evrendeki entropi miktari zaman icinde giderek arttigi icin etrafimizdaki enerji miktari da zaman icerisi azalacak ve isi olumu yasanacagi ve bunun bir sonucu olarak da fiziksel anlamda hicbir is yapilamayacak ve dunya uzerindeki hayatin sona erecegi de soylenenler arasindadir Bir yandan da surekli genisleyen bir evrenin icinde oldugumuzu dusunecek olursak isil dengeye hicbir zaman ulasilamayacak ve bu isi olumu kurami curutmeye yetecektir Kainatin su anki durumunu goz onune alacak olursak one cikan fikirlerden biri kainat bize muhtemelen evrendeki butun enerji kaynaklarinin yok olacagi yildizlarin bile sonecegi bir gelecek sunacaktir Bununla beraber belki de kucuk parcaciklardan olusan sistemlerden az miktarda da olsa enerji uretmek mumkun olur ve son derece dusuk enerji seviyelerinde de olsa ilginc olaylar yasanmaya devam edebilir Kaynakca Carnot S 1824 1986 1980 Chapter 5 Adkins C J 1968 1983 s 56 58 Munster A 1970 s 11 Kondepudi D Prigogine I 1998 s 67 75 Lebon G Jou D Casas Vazquez J 2008 s 10 Eu B C 2002 s 32 35 Clausius R 1850 Clausius R 1867 Thomson W 1851 a b Munster A 1970 s 45 a b Lieb E H Yngvason J 1999 s 49 Muncaster R G 1980 Fundamentals of Maxwell s Kinetic Theory of a Simple Monatomic Gas Treated as a Branch of Rational Mechanics Academic Press New York ISBN0 12 701350 4 s 15 Planck M 1926 s 457 Vikipedi editorunun cevirisi 1909 Buchdahl H A 1966 p 68 Sychev V V 1991 The Differential Equations of Thermodynamics Taylor amp Francis ISBN 978 1560321217 Erisim tarihi 26 Kasim 2012 Planck M 1926 Buchdahl H A 1966 s 69
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans