Bu madde önerilmeyen biçimde kaynaklandırılmıştır. () |
Bu maddedeki üslubun, ansiklopedik bir yazıdan beklenen resmî ve ciddi üsluba uygun olmadığı düşünülmektedir. |
büyüklüğünün veya mutlak sıcaklık ya da termodinamik sıcaklık olarak tanımlanan büyüklüğünün iki önemli fiziksel sonucu vardır.
- Ayrı ayrı dengede bulunan ve aynı değerdeki büyüklüklerle tanımlanan iki sistem birbirlerine dokunduğunda denge korunur ve hiçbir enerji alışverişi olmaz.
- Sistemleri tanımlayan büyüklükler farklı ise sistemler birbirine dokundurulduğunda enerji alışverişi olur.
Ayrı olarak dengede olan A, B ve C sistemlerini göz önüne alalım. C, A'ya ve C, B'ye dokundurulduğunda aralarında enerji alışverişi olmuyorsa, ve eşitliği doğrudur. Bu bize termodinamiğin sıfırıncı yasasını verir, bu yasa " İki sistem bir üçüncü sistemle ısısal dengede ise, bu iki sistem birbirleri ile ısısal dengededir " şeklinde ifade edilir. İki sistemin dengede olması koşulunu veren sıfırıncı yasa, sistemler birbirlerine dokundurulduklarında ısı alışverişi yapıp yapmayacaklarını test edebileceğimiz, termometre adı verilen deneme sistemlerinin temelini sağlar. Böyle bir M termometresi şu iki kurala uymalıdır.
- M termometresi etkileşmeye bırakıldığında değişen tek bir parametresi olmalıdır. Buna diyelim. büyüklüğüne "termometrik büyüklük" denir.
- M termometresinin ölçüm yaptığı sistemin toplam enerjisinde büyük değişikliklere sebep olmaması amacıyla, ölçüm yapacağı sistemlerden daha küçük boyutlarda seçilmesi gerekmektedir.
Sonuç olarak, A ve B sistemleriyle sırasıyla dengeye gelmeye bırakılan M sistemi (termometresi) A ve B için büyüklüğünü belirler. Buna göre A ve B'nin birbirlerine dokundurulduklarında enerji alışverişi yapıp yapmayacağı anlaşılır.
Mutlak sıcaklık
Burada konu edilen sıcaklık M sisteminin kendisine bağlı olduğundan rastgeledir. Bu kavramı mutlak duruma getirmek için 
Bir M termometresinde, 





termometre, A sisteminin temel özelliği olan enerji ile girilebilir durumlarının parçalı artışını ölçer. Başka bir N termometresi 




Bu sonuca bağlı olarak 

büyüklüğüne mutlak sıcaklık denir.
Mutlak sıcaklığın özellikleri

denklemine göre, mutlak sıcaklık, 




tanımıyla verilir. 


olmasını gerektirir.
- Özellik 1: Herhangi bir sistemin mutlak sıcaklığı sıfırdan büyüktür.
Gelişigüzel bir sistemde 



olmalıdır.
Sonuç olarak
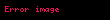


bulunur.
- Özellik 2:
büyüklüğü, T mutlak sıcaklığına sahip sistem için yaklaşık olarak sistemin serbestlik derecesi başına düşen ortalama enerjiye denktir.
Isısal etkileşmede bulunan sistemlerin dengede olma koşulu sistemlerin mutlak sıcaklık büyüklüklerinin eşit olmasıdır. Buna göre, etkileşen sistemlerin toplam enerjileri, sistemlerin serbestlik dereceleri başına düşen enerjilerin her biri için eşit olacak şekilde paylaşılır.
T büyüklüğü, sistemin E enerjisiyle değişir. Çünkü, 
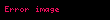


şeklindedir. Aynı sonuç 
- Özellik 3: Bir sistemin mutlak sıcaklığı, sistemin enerjisinin artan bir fonksiyonudur.
İlk üç özelliğin sonucu olarak
- Özellik 4: İki sistem ısısal etkileşmeye girdiklerinde, "pozitif ısı" ("pozitif enerji") akışı mutlak sıcaklığı görece büyük olandan küçük olan sisteme doğrudur. İstatistik fiziğin tanımlarıyla çelişmeyen şu ifade de doğrudur; Mutlak sıcaklığı küçük olan sistem mutlak sıcaklığı büyük olan sisteme "negatif ısı" aktarır.
Ayrıca bakınız
Kaynakça
- Landau L.D., Lifshitz E.M., Statistical Physics Part 1, Pergamon Press 1959, Chapter 2
- Reif F., Statistical Physics, Berkeley Physics Lectures, Chapter 3 and 4
- ^ . NobelPrize.org (İngilizce). 19 Eylül 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Mart 2021.
- ^ . Maths History (İngilizce). 4 Aralık 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Mart 2021.
- ^ . Encyclopedia Britannica (İngilizce). 12 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Mart 2021.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde onerilmeyen bicimde kaynaklandirilmistir Gosterilen kaynaklar kaynak gosterme sablonlari kullanilarak dipnot belirtme bicemine uygun olarak duzenlenmelidir Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Bu maddedeki uslubun ansiklopedik bir yazidan beklenen resmi ve ciddi usluba uygun olmadigi dusunulmektedir Maddeyi gelistirerek ya da konuyla ilgili tartismaya katilarak Vikipedi ye katkida bulunabilirsiniz b displaystyle beta buyuklugunun veya mutlak sicaklik ya da termodinamik sicaklik olarak tanimlanan T kb 1 displaystyle T equiv k beta 1 buyuklugunun iki onemli fiziksel sonucu vardir Ayri ayri dengede bulunan ve ayni degerdeki buyukluklerle tanimlanan iki sistem birbirlerine dokundugunda denge korunur ve hicbir enerji alisverisi olmaz Sistemleri tanimlayan buyuklukler farkli ise sistemler birbirine dokunduruldugunda enerji alisverisi olur Ayri olarak dengede olan A B ve C sistemlerini goz onune alalim C A ya ve C B ye dokunduruldugunda aralarinda enerji alisverisi olmuyorsa bA bC displaystyle beta A beta C ve bB bC displaystyle beta B beta C esitligi dogrudur Bu bize termodinamigin sifirinci yasasini verir bu yasa Iki sistem bir ucuncu sistemle isisal dengede ise bu iki sistem birbirleri ile isisal dengededir seklinde ifade edilir Iki sistemin dengede olmasi kosulunu veren sifirinci yasa sistemler birbirlerine dokundurulduklarinda isi alisverisi yapip yapmayacaklarini test edebilecegimiz termometre adi verilen deneme sistemlerinin temelini saglar Boyle bir M termometresi su iki kurala uymalidir M termometresi etkilesmeye birakildiginda degisen tek bir parametresi olmalidir Buna 8 displaystyle theta diyelim 8 displaystyle theta buyuklugune termometrik buyukluk denir M termometresinin olcum yaptigi sistemin toplam enerjisinde buyuk degisikliklere sebep olmamasi amaciyla olcum yapacagi sistemlerden daha kucuk boyutlarda secilmesi gerekmektedir Sonuc olarak A ve B sistemleriyle sirasiyla dengeye gelmeye birakilan M sistemi termometresi A ve B icin 8 displaystyle theta buyuklugunu belirler Buna gore A ve B nin birbirlerine dokundurulduklarinda enerji alisverisi yapip yapmayacagi anlasilir Mutlak sicaklikBurada konu edilensicaklikM sisteminin kendisine bagli oldugundan rastgeledir Bu kavrami mutlak duruma getirmek icin b displaystyle beta kavramini anlamak gerekir Bir M termometresinde b displaystyle beta buyuklugu 8 displaystyle theta termometrik buyuklugunun bir fonksiyonu olsun Bu termometre bir A sistemiyle isisal dengede ise denge durumunda b bA displaystyle beta beta A olur E displaystyle E sistemin toplam enerjisi ve W displaystyle Omega girilebilir durumlarinin sayisi olmak uzere b E ln W E 1W W E displaystyle beta E frac partial ln Omega partial E frac 1 Omega frac partial Omega partial E termometre A sisteminin temel ozelligi olan enerji ile girilebilir durumlarinin parcali artisini olcer Baska bir N termometresi 8 displaystyle theta prime termometrik buyuklugunun ve b displaystyle beta prime buyuklugunun fonksiyonu olsun N termometresi A sistemine dokunduruldugunda denge durumunda b b displaystyle beta prime beta olur b displaystyle beta buyuklugu bir termometrenin termometrik buyuklugu ise ayni b displaystyle beta yla verilen her termometre ayni A sisteminin sicakligini esit degerde gosterir Termometrenin gosterdigi sicaklik degeri ayni zamanda uzerinde olcum yapilan sistemin girilebilir durumlarinin sayisi ni verir Bu sonuca bagli olarak b displaystyle beta nin bir fonksiyonu olarak tanimlanan T kb 1 displaystyle T equiv k beta 1 buyuklugune mutlak sicaklik denir Mutlak sicakligin ozelliklerib E ln W E 1W W E displaystyle beta E frac partial ln Omega partial E frac 1 Omega frac partial Omega partial E denklemine gore mutlak sicaklik k displaystyle k Boltzmann sabiti ve W E displaystyle Omega E sistemin E displaystyle E ile E dE displaystyle E delta E enerji araligindaki girilebilir durumlarinin sayisi olmak uzere 1kT b ln W E displaystyle frac 1 kT equiv beta equiv frac partial ln Omega partial E tanimiyla verilir W E displaystyle Omega E herhangi bir sistemde E enerjisinin hizli artan bir fonksiyonu oldugu icin yukaridaki denklemde b gt 0 displaystyle beta gt 0 T gt 0 displaystyle T gt 0 olmasini gerektirir Ozellik 1 Herhangi bir sistemin mutlak sicakligi sifirdan buyuktur Gelisiguzel bir sistemde W E displaystyle Omega E nin E enerjisinin hizli artan bir fonksiyonu olmasi yaklasik olarak f displaystyle f sistemin serbestlik derecesi ve E0 displaystyle E 0 taban durumu enerjisi olmak uzere W E E E0 f displaystyle Omega E propto E E 0 f olmalidir Sonuc olarak ln W fln E E0 sabit displaystyle ln Omega propto f ln E E 0 sabit b ln W E fE E0 displaystyle beta equiv frac partial ln Omega partial E sim frac f E E 0 olup ve de T nin buyuklugu serbestlik derecesi basina dusen ortalama enerjiye esit alinabildiginden kT 1b E E0f displaystyle kT equiv frac 1 beta sim frac bar E E 0 f bulunur Ozellik 2 kT displaystyle kT buyuklugu T mutlak sicakligina sahip sistem icin yaklasik olarak sistemin serbestlik derecesi basina dusen ortalama enerjiye denktir Isisal etkilesmede bulunan sistemlerin dengede olma kosulu sistemlerin mutlak sicaklik buyukluklerinin esit olmasidir Buna gore etkilesen sistemlerin toplam enerjileri sistemlerin serbestlik dereceleri basina dusen enerjilerin her biri icin esit olacak sekilde paylasilir T buyuklugu sistemin E enerjisiyle degisir Cunku b displaystyle beta buyuklugu ln W displaystyle ln Omega E displaystyle E uzayinda cizilen fonksiyonun egimidir Bunu tanimlayan matematiksel baginti b E lt 0 displaystyle frac partial beta partial E lt 0 seklindedir Ayni sonuc b displaystyle beta nin matematiksel tanimindan da cikarilabilir Ozellik 3 Bir sistemin mutlak sicakligi sistemin enerjisinin artan bir fonksiyonudur Ilk uc ozelligin sonucu olarak Ozellik 4 Iki sistem isisal etkilesmeye girdiklerinde pozitif isi pozitif enerji akisi mutlak sicakligi gorece buyuk olandan kucuk olan sisteme dogrudur Istatistik fizigin tanimlariyla celismeyen su ifade de dogrudur Mutlak sicakligi kucuk olan sistem mutlak sicakligi buyuk olan sisteme negatif isi aktarir Ayrica bakinizSicaklik Mutlak sifirKaynakcaLandau L D Lifshitz E M Statistical Physics Part 1 Pergamon Press 1959 Chapter 2 Reif F Statistical Physics Berkeley Physics Lectures Chapter 3 and 4 NobelPrize org Ingilizce 19 Eylul 2018 tarihinde kaynagindan arsivlendi Erisim tarihi 28 Mart 2021 Maths History Ingilizce 4 Aralik 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 28 Mart 2021 Encyclopedia Britannica Ingilizce 12 Temmuz 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 28 Mart 2021
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans


