Düzgün dairesel hareket, sabit bir kuvvetin etkisinde, bir çember üzerinde süratin değişmediği harekettir.
Periyot ve frekans
Periyot
Düzgün dairesel harekette bir tam dolanım için geçen süredir. 
Frekans
Düzgün dairesel hareket yapan cismin bir saniyedeki dolanım sayısıdır. 
Periyot ve frekans arasında, 
Hız

Çember üzerinde dolanan bir cisim, Şekil 1 deki gibi 

Çizgisel hız
Şekil 1 deki gibi düzgün dairesel hareket yapan bir cismin, daire yayı üzerinde birim zamanda aldığı yola çizgisel hız denir. Çizgisel hız vektörü (
Düzgün doğrusal harekette; 


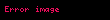
Bu nedenle çizgisel hız ifadesi;
şeklinde bulunur. Çizgisel hızın birimi metre / saniye dir.
Açısal hız
Cismi merkeze bağlayan yarıçap vektörünün, birim zamanda radyan cinsinden taradığı açıya açısal hız denir, ω ile gösterilir. Birimi rad/s dir.
Dairesel hareket yapan bir cismi merkeze bağlayan yarıçap vektörü bir tam devir yaptığında, 
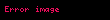
olur.
Çizgisel hız ile açısal hız arasındaki bağıntı ise;
olmak üzere
olur.
İvme ve kuvvet
Merkezcil ivme

Dairesel bir yörüngede sabit hızla dönen bir cismin, eşit zaman aralıklarıyla çizilmiş hız vektörleri Şekil 3 teki gibi olur. Bu hız vektörlerinin büyüklükleri eşit, yönleri ise farklıdır.
Hız vektörlerinin başlangıç noktaları ortak bir noktada toplanırsa ardışık 


olur.
Ani ivme vektörleri, hız vektörlerine diktir.
Düzgün dairesel hareket yapan bir cisim, 




olur. Çizgisel hızın 
veya
bulunur.
Dairesel harekette bu ivmeye merkezcil ivme denir.

Buradaki 

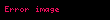
Merkezcil kuvvet
Her ivme, kendi yönünde bir net kuvvet tarafından oluşturulur. Düzgün dairesel harekette de cisme ivme kazandıran kuvvet dinamiğin temel prensibi olan 
Bu kuvvetin yönü, ivme ile aynı yönlü olup yörüngenin merkezine doğrudur. Bu kuvvete merkezcil kuvvet denir. Kuvvetin büyüklüğü, 

şeklinde de yazılabilir.
Merkezkaç kuvveti

Dairesel harekette merkezkaç kuvveti adı verilen bir kuvvet daha vardır. Newton yasalarının geçerli olduğu bir referans sisteminde böyle bir kuvvet yoktur. Bu kuvvetin çıkma sebebi gözlemcinin sistemde Newton yasalarını uygulayabilmek için varsaydığı eylemsizlik kuvvetidir (Şekil 5).
Düzgün dairesel hareketin uygulamaları
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Duzgun dairesel hareket sabit bir kuvvetin etkisinde bir cember uzerinde suratin degismedigi harekettir Periyot ve frekansPeriyot Duzgun dairesel harekette bir tam dolanim icin gecen suredir T displaystyle T ile gosterilir Birimi saniyedir Frekans Duzgun dairesel hareket yapan cismin bir saniyedeki dolanim sayisidir f displaystyle f ile gosterilir Birimi Hertz dir Periyot ve frekans arasinda f 1T displaystyle f 1 over T bagintisi vardir HizSekil 1 Cember uzerinde dolanan bir cisim Sekil 1 deki gibi x displaystyle x kadar yol alirken yaricap vektoru ayni anda 8 displaystyle theta acisi kadar bir aci tarar Bu nedenle dairesel hareketlerde biri cizgisel digeri acisal olmak uzere iki cesit hiz tanimlanir Cizgisel hiz Sekil 1 deki gibi duzgun dairesel hareket yapan bir cismin daire yayi uzerinde birim zamanda aldigi yola cizgisel hiz denir Cizgisel hiz vektoru v displaystyle overrightarrow v daire yayina tam teget olup yaricap vektorune diktir Duzgun dogrusal harekette HIZ YolZaman displaystyle text HIZ Yol over Zaman veya v xt displaystyle v x over t idi Cisim dairenin tum cevresini dolanirsa 2pr displaystyle 2 pi r kadar yol alir ve bu esnada bir periyot T displaystyle T kadar zaman gecer Bu nedenle cizgisel hiz ifadesi 2pr v T displaystyle 2 pi r v T v 2prT displaystyle v 2 pi r over T v 2prf displaystyle v 2 pi rf seklinde bulunur Cizgisel hizin birimi metre saniye dir Acisal hiz Cismi merkeze baglayan yaricap vektorunun birim zamanda radyan cinsinden taradigi aciya acisal hiz denir w ile gosterilir Birimi rad s dir Dairesel hareket yapan bir cismi merkeze baglayan yaricap vektoru bir tam devir yaptiginda 2p displaystyle 2 pi radyan aci tarar ve bu esnada bir periyot T displaystyle T kadar zaman gecer O halde acisal hiz 8 w t displaystyle theta omega t 2p w t displaystyle 2 pi omega t w 2pT displaystyle omega 2 pi over T w 2pf displaystyle omega 2 pi f olur Cizgisel hiz ile acisal hiz arasindaki baginti ise w 2pT displaystyle omega 2 pi over T olmak uzerev 2prT displaystyle v 2 pi r over T v w r displaystyle v omega r olur Ivme ve kuvvetMerkezcil ivme Sekil 3 Dairesel bir yorungede sabit hizla donen bir cismin esit zaman araliklariyla cizilmis hiz vektorleri Sekil 3 teki gibi olur Bu hiz vektorlerinin buyuklukleri esit yonleri ise farklidir Hiz vektorlerinin baslangic noktalari ortak bir noktada toplanirsa ardisik Dv displaystyle Delta overrightarrow v hiz degisim vektorlerinin esit buyuklukte fakat farkli yonlerde oldugu gorulur Dt displaystyle Delta t suresindeki hiz degisim vektoru Dv displaystyle Delta overrightarrow v ise ortalama ivme vektoru a ort Dv Dt displaystyle overrightarrow a ort Delta overrightarrow v over Delta t olur Ani ivme vektorleri hiz vektorlerine diktir Duzgun dairesel hareket yapan bir cisim R displaystyle R yaricapli cember uzerinde bir devir yaptiginda hiz vektoru de tam bir devir yaparak baslangictaki yonune gelir Diger bir deyisle hiz vektorunun ucu r displaystyle r yaricapli bir dairenin 2pr displaystyle 2 pi r cevresini T displaystyle T zamanda doner Hizdaki degisim Dv 2pr displaystyle Delta v 2 pi r oldugundan a 2prT displaystyle a 2 pi r over T olur Cizgisel hizin v 2pRT displaystyle v 2 pi R over T degeri ivme bagintisinda yerine yazilirsa a 4p2RT2 displaystyle a 4 pi 2 R over T 2 veyaa v2R w2R displaystyle a v 2 over R omega 2 R bulunur Dairesel harekette bu ivmeye merkezcil ivme denir Sekil 4 Buradaki displaystyle isareti R displaystyle overrightarrow R vektoruyle a displaystyle overrightarrow a ivme vektorunun ayni dogrultuda ve ters yonlu oldugunu gosterir Sekil 4 Merkezcil kuvvet Her ivme kendi yonunde bir net kuvvet tarafindan olusturulur Duzgun dairesel harekette de cisme ivme kazandiran kuvvet dinamigin temel prensibi olan F m a displaystyle overrightarrow F m overrightarrow a dan F m 4p2R T2 displaystyle overrightarrow F m 4 pi 2 overrightarrow R over T 2 Bu kuvvetin yonu ivme ile ayni yonlu olup yorungenin merkezine dogrudur Bu kuvvete merkezcil kuvvet denir Kuvvetin buyuklugu v displaystyle v hizi ile R displaystyle R yaricapina bagli olarak F m 4p2RT2 mv2R displaystyle F m 4 pi 2 R over T 2 mv 2 over R seklinde de yazilabilir Merkezkac kuvveti Sekil 5 Dairesel harekette merkezkac kuvveti adi verilen bir kuvvet daha vardir Newton yasalarinin gecerli oldugu bir referans sisteminde boyle bir kuvvet yoktur Bu kuvvetin cikma sebebi gozlemcinin sistemde Newton yasalarini uygulayabilmek icin varsaydigi eylemsizlik kuvvetidir Sekil 5 Duzgun dairesel hareketin uygulamalariEgimli viraj Yatay viraj
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State














