Matematikte, bir trigonometrik yerine koyma veya trigonometrik ikame, trigonometrik fonksiyon yerine başka bir ifadeyi koyar. Kalkülüste trigonometrik ikameler integralleri hesaplamak için kullanılan bir tekniktir. Bu durumda, içeren bir ifade trigonometrik bir ifade ile değiştirilir. Trigonometrik özdeşlikler cevabı basitleştirmeye yardımcı olabilir. Diğer yerine koyma yoluyla integrasyon yöntemlerinde olduğu gibi, belirli bir integrali değerlendirirken, integrasyon sınırlarını uygulamadan önce, ters türevin sonucunu tam olarak çıkarmak daha basit olabilir.
Durum I: a2 − x2 içeren integraller


Durum I için örnekler

Örnek 1

integralinde,

ikamesini kullanabiliriz. Böylece,

Yukarıdaki adım 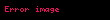




Belirli bir integral için, integrasyon sınırlarının nasıl değiştiğini bulmak gerekir. Örneğin, 

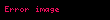


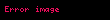




Sınırları seçerken biraz dikkatli olmak gerekir. Yukarıdaki integral 






Alternatif olarak, sınır koşullarını uygulamadan önce belirsiz integralleri tam olarak değerlendirin. Bu durumda, ters türev daha önce olduğu gibi şu sonucu verir:

Örnek 2

integrali, 
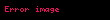




Böylece, 
Belirli bir integral için, yerine koyma işlemi gerçekleştirildikten sonra sınırlar değişir ve 

Örneğin,

belirli integrali, 




Öte yandan, sınır terimlerinin daha önce elde edilen ters türev formülüne doğrudan uygulanması, daha önce olduğu gibi aşağıdaki sonucu verir:

Durum II: a2 + x2 içeren integraller
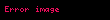

Durum II için örnekler

Örnek 1

integralinde,

yazabiliriz, böylece integral şu hale gelir:


Belirli bir integral için sınırlar, ikame işlemi gerçekleştirildikten sonra değişir ve 

Örneğin,

belirli integrali, 




Bu arada, sınır terimlerinin ters türev formülüne doğrudan uygulanması, daha önceki gibi aşağıdaki sonucu verir:

Örnek 2

integrali,

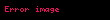




Öyleyse, 
, kullanılarak hesaplanabilir. Sonuç olarak,

Durum III: x2 − a2 içeren integraller


Durum III için örnekler


şeklindeki integraller, trigonometrik ikameler yerine ile de hesaplanabilir. Bununla birlikte,

integrali hesaplanamaz. Bu durumda, uygun bir ikame şudur:

burada 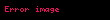





Öyleyse, 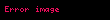
Pay ve paydayı 





Trigonometrik fonksiyonları ortadan kaldıran ikameler
Trigonometrik fonksiyonları yok etmek için ikame kullanılabilir. Örneğin,

Son ikame, olarak bilinir ve kullanır. Örneğin,
Hiperbolik yerine koyma
İntegralleri basitleştirmek için hiperbolik fonksiyonların ikameleri de kullanılabilir.
Örneğin, 




İstenirse, bu sonuç başka özdeşlikler kullanılarak da dönüştürülebilir, örneğin bağıntısını:

Ayrıca bakınız


- (Weierstrass ikamesi veya Tanjant yarım açı ikamesi)
- (Euler ikamesi)
Kaynakça
- ^ (2008). Calculus: Early Transcendentals
![image]() . 6. . ISBN .
. 6. . ISBN . - ^ ; Weir, Maurice D.; (2010). Thomas' Calculus: Early Transcendentals. 12. Addison-Wesley. ISBN .
- ^ (2012). "Section 7.2: Trigonometric Integrals". Calculus - Early Transcendentals. United States: Cengage Learning. ss. 475-6. ISBN .
- ^ Boyadzhiev, Khristo N. "Hyperbolic Substitutions for Integrals" (PDF). 26 Şubat 2020 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 4 Mart 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir trigonometrik yerine koyma veya trigonometrik ikame trigonometrik fonksiyon yerine baska bir ifadeyi koyar Kalkuluste trigonometrik ikameler integralleri hesaplamak icin kullanilan bir tekniktir Bu durumda iceren bir ifade trigonometrik bir ifade ile degistirilir Trigonometrik ozdeslikler cevabi basitlestirmeye yardimci olabilir Diger yerine koyma yoluyla integrasyon yontemlerinde oldugu gibi belirli bir integrali degerlendirirken integrasyon sinirlarini uygulamadan once ters turevin sonucunu tam olarak cikarmak daha basit olabilir Durum I a2 x2 iceren integrallerx asin 8 displaystyle x a sin theta olsun ve 1 sin2 8 cos2 8 displaystyle 1 sin 2 theta cos 2 theta ozdesligini kullanin Durum I icin ornekler Durum I icin geometrik yapiOrnek 1 dxa2 x2 displaystyle int frac dx sqrt a 2 x 2 integralinde x asin 8 dx acos 8d8 8 arcsin xa displaystyle x a sin theta quad dx a cos theta d theta quad theta arcsin frac x a ikamesini kullanabiliriz Boylece dxa2 x2 acos 8d8a2 a2sin2 8 acos 8d8a2 1 sin2 8 acos 8d8a2cos2 8 d8 8 C arcsin xa C displaystyle begin aligned int frac dx sqrt a 2 x 2 amp int frac a cos theta d theta sqrt a 2 a 2 sin 2 theta 6pt amp int frac a cos theta d theta sqrt a 2 1 sin 2 theta 6pt amp int frac a cos theta d theta sqrt a 2 cos 2 theta 6pt amp int d theta 6pt amp theta C 6pt amp arcsin frac x a C end aligned Yukaridaki adim a gt 0 displaystyle a gt 0 ve cos 8 gt 0 displaystyle cos theta gt 0 olmasini gerektirir a displaystyle a yi a2 displaystyle a 2 nin ana koku olarak secebilir ve ters sinus fonksiyonunu kullanarak p 2 lt 8 lt p 2 displaystyle pi 2 lt theta lt pi 2 kisitlamasini uygulayabiliriz Belirli bir integral icin integrasyon sinirlarinin nasil degistigini bulmak gerekir Ornegin x displaystyle x 0 displaystyle 0 dan a 2 displaystyle a 2 ye giderken sin 8 displaystyle sin theta 0 displaystyle 0 dan 1 2 displaystyle 1 2 ye gider boylece 8 displaystyle theta 0 displaystyle 0 dan p 6 displaystyle pi 6 ya gider Oyleyse 0a 2dxa2 x2 0p 6d8 p6 displaystyle int 0 a 2 frac dx sqrt a 2 x 2 int 0 pi 6 d theta frac pi 6 Sinirlari secerken biraz dikkatli olmak gerekir Yukaridaki integral p 2 lt 8 lt p 2 displaystyle pi 2 lt theta lt pi 2 gerektirdiginden 8 displaystyle theta yalnizca 0 displaystyle 0 ile p 6 displaystyle pi 6 arasinda olabilir Bu kisitlama ihmal edildiginde 8 displaystyle theta nin p displaystyle pi den 5p 6 displaystyle 5 pi 6 ya gitmesi secilebilirdi bu da gercek degerin negatifiyle sonuclanirdi Alternatif olarak sinir kosullarini uygulamadan once belirsiz integralleri tam olarak degerlendirin Bu durumda ters turev daha once oldugu gibi su sonucu verir 0a 2dxa2 x2 arcsin xa 0a 2 arcsin 12 arcsin 0 p6 displaystyle int 0 a 2 frac dx sqrt a 2 x 2 arcsin left frac x a right Biggl 0 a 2 arcsin left frac 1 2 right arcsin 0 frac pi 6 Ornek 2 a2 x2dx displaystyle int sqrt a 2 x 2 dx integrali x asin 8 dx acos 8d8 8 arcsin xa x a sin theta dx a cos theta d theta theta arcsin dfrac x a burada a gt 0 displaystyle a gt 0 olarak alinarak hesaplanabilir boylece a2 a sqrt a 2 a ve p 2 8 p 2 pi 2 leq theta leq pi 2 arksin deger kumesine gore cos 8 0 displaystyle cos theta geq 0 ve cos2 8 cos 8 textstyle sqrt cos 2 theta cos theta dir Boylece a2 x2dx a2 a2sin2 8 acos 8 d8 a2 1 sin2 8 acos 8 d8 a2 cos2 8 acos 8 d8 acos 8 acos 8 d8 a2 cos2 8d8 a2 1 cos 282 d8 a22 8 12sin 28 C a22 8 sin 8cos 8 C a22 arcsin xa xa1 x2a2 C a22arcsin xa x2a2 x2 C displaystyle begin aligned int sqrt a 2 x 2 dx amp int sqrt a 2 a 2 sin 2 theta a cos theta d theta 6pt amp int sqrt a 2 1 sin 2 theta a cos theta d theta 6pt amp int sqrt a 2 cos 2 theta a cos theta d theta 6pt amp int a cos theta a cos theta d theta 6pt amp a 2 int cos 2 theta d theta 6pt amp a 2 int left frac 1 cos 2 theta 2 right d theta 6pt amp frac a 2 2 left theta frac 1 2 sin 2 theta right C 6pt amp frac a 2 2 theta sin theta cos theta C 6pt amp frac a 2 2 left arcsin frac x a frac x a sqrt 1 frac x 2 a 2 right C 6pt amp frac a 2 2 arcsin frac x a frac x 2 sqrt a 2 x 2 C end aligned Belirli bir integral icin yerine koyma islemi gerceklestirildikten sonra sinirlar degisir ve 8 arcsin xa theta arcsin dfrac x a denklemi kullanilarak p 2 8 p 2 pi 2 leq theta leq pi 2 araligindaki degerlerle belirlenir Alternatif olarak sinir terimlerini dogrudan ters turev formulune uygulayin Ornegin 114 x2dx displaystyle int 1 1 sqrt 4 x 2 dx belirli integrali x 2sin 8 dx 2cos 8d8 displaystyle x 2 sin theta dx 2 cos theta d theta yerine 8 arcsin x2 theta arcsin dfrac x 2 kullanilarak belirlenen sinirlarla hesaplanabilir arcsin 1 2 p 6 displaystyle arcsin 1 2 pi 6 ve arcsin 1 2 p 6 displaystyle arcsin 1 2 pi 6 oldugundan 114 x2dx p 6p 64 4sin2 8 2cos 8 d8 p 6p 64 1 sin2 8 2cos 8 d8 p 6p 64 cos2 8 2cos 8 d8 p 6p 6 2cos 8 2cos 8 d8 4 p 6p 6cos2 8d8 4 p 6p 6 1 cos 282 d8 2 8 12sin 28 p 6p 6 28 sin 28 p 6p 6 p3 sin p3 p3 sin p3 2p3 3 displaystyle begin aligned int 1 1 sqrt 4 x 2 dx amp int pi 6 pi 6 sqrt 4 4 sin 2 theta 2 cos theta d theta 6pt amp int pi 6 pi 6 sqrt 4 1 sin 2 theta 2 cos theta d theta 6pt amp int pi 6 pi 6 sqrt 4 cos 2 theta 2 cos theta d theta 6pt amp int pi 6 pi 6 2 cos theta 2 cos theta d theta 6pt amp 4 int pi 6 pi 6 cos 2 theta d theta 6pt amp 4 int pi 6 pi 6 left frac 1 cos 2 theta 2 right d theta 6pt amp 2 left theta frac 1 2 sin 2 theta right pi 6 pi 6 2 theta sin 2 theta Biggl pi 6 pi 6 6pt amp left frac pi 3 sin frac pi 3 right left frac pi 3 sin left frac pi 3 right right frac 2 pi 3 sqrt 3 end aligned Ote yandan sinir terimlerinin daha once elde edilen ters turev formulune dogrudan uygulanmasi daha once oldugu gibi asagidaki sonucu verir 114 x2dx 222arcsin x2 x222 x2 11 2arcsin 12 124 1 2arcsin 12 124 1 2 p6 32 2 p6 32 2p3 3 displaystyle begin aligned int 1 1 sqrt 4 x 2 dx amp left frac 2 2 2 arcsin frac x 2 frac x 2 sqrt 2 2 x 2 right 1 1 6pt amp left 2 arcsin frac 1 2 frac 1 2 sqrt 4 1 right left 2 arcsin left frac 1 2 right frac 1 2 sqrt 4 1 right 6pt amp left 2 cdot frac pi 6 frac sqrt 3 2 right left 2 cdot left frac pi 6 right frac sqrt 3 2 right 6pt amp frac 2 pi 3 sqrt 3 end aligned Durum II a2 x2 iceren integrallerx atan 8 displaystyle x a tan theta olsun ve 1 tan2 8 sec2 8 displaystyle 1 tan 2 theta sec 2 theta ozdesligini kullanin Durum II icin ornekler Durum II icin geometrik yapiOrnek 1 dxa2 x2 displaystyle int frac dx a 2 x 2 integralinde x atan 8 dx asec2 8d8 8 arctan xa displaystyle x a tan theta quad dx a sec 2 theta d theta quad theta arctan frac x a yazabiliriz boylece integral su hale gelir dxa2 x2 asec2 8d8a2 a2tan2 8 asec2 8d8a2 1 tan2 8 asec2 8d8a2sec2 8 d8a 8a C 1aarctan xa C displaystyle begin aligned int frac dx a 2 x 2 amp int frac a sec 2 theta d theta a 2 a 2 tan 2 theta 6pt amp int frac a sec 2 theta d theta a 2 1 tan 2 theta 6pt amp int frac a sec 2 theta d theta a 2 sec 2 theta 6pt amp int frac d theta a 6pt amp frac theta a C 6pt amp frac 1 a arctan frac x a C end aligned a 0 displaystyle a neq 0 olmak kosuluyla Belirli bir integral icin sinirlar ikame islemi gerceklestirildikten sonra degisir ve 8 arctan xa displaystyle theta arctan frac x a denklemi kullanilarak p2 lt 8 lt p2 displaystyle frac pi 2 lt theta lt frac pi 2 araligindaki degerlerle belirlenir Alternatif olarak sinir terimlerini dogrudan ters turev formulune uygulayin Ornegin 014dx1 x2 displaystyle int 0 1 frac 4 dx 1 x 2 belirli integrali x tan 8 dx sec2 8d8 displaystyle x tan theta dx sec 2 theta d theta yerine 8 arctan x displaystyle theta arctan x kullanilarak belirlenen sinirlar ile hesaplanabilir arctan 0 0 displaystyle arctan 0 0 ve arctan 1 p 4 displaystyle arctan 1 pi 4 oldugundan 014dx1 x2 4 01dx1 x2 4 0p 4sec2 8d81 tan2 8 4 0p 4sec2 8d8sec2 8 4 0p 4d8 48 0p 4 4 p4 0 p displaystyle begin aligned int 0 1 frac 4 dx 1 x 2 amp 4 int 0 1 frac dx 1 x 2 6pt amp 4 int 0 pi 4 frac sec 2 theta d theta 1 tan 2 theta 6pt amp 4 int 0 pi 4 frac sec 2 theta d theta sec 2 theta 6pt amp 4 int 0 pi 4 d theta 6pt amp 4 theta Bigg 0 pi 4 4 left frac pi 4 0 right pi end aligned Bu arada sinir terimlerinin ters turev formulune dogrudan uygulanmasi daha onceki gibi asagidaki sonucu verir 014dx1 x2 4 01dx1 x2 4 11arctan x1 01 4 arctan x 01 4 arctan 1 arctan 0 4 p4 0 p displaystyle begin aligned int 0 1 frac 4 dx 1 x 2 amp 4 int 0 1 frac dx 1 x 2 6pt amp 4 left frac 1 1 arctan frac x 1 right 0 1 6pt amp 4 arctan x Bigg 0 1 6pt amp 4 arctan 1 arctan 0 6pt amp 4 left frac pi 4 0 right pi end aligned Ornek 2 a2 x2dx displaystyle int sqrt a 2 x 2 dx integrali x atan 8 dx asec2 8d8 8 arctan xa displaystyle x a tan theta dx a sec 2 theta d theta theta arctan frac x a alinarak hesaplanabilir Burada a gt 0 displaystyle a gt 0 boylece a2 a displaystyle sqrt a 2 a ve p2 lt 8 lt p2 displaystyle frac pi 2 lt theta lt frac pi 2 arctanjant deger kumesine gore sec 8 gt 0 displaystyle sec theta gt 0 ve sec2 8 sec 8 displaystyle sqrt sec 2 theta sec theta dir Oyleyse a2 x2dx a2 a2tan2 8 asec2 8 d8 a2 1 tan2 8 asec2 8 d8 a2sec2 8 asec2 8 d8 asec 8 asec2 8 d8 a2 sec3 8d8 displaystyle begin aligned int sqrt a 2 x 2 dx amp int sqrt a 2 a 2 tan 2 theta a sec 2 theta d theta 6pt amp int sqrt a 2 1 tan 2 theta a sec 2 theta d theta 6pt amp int sqrt a 2 sec 2 theta a sec 2 theta d theta 6pt amp int a sec theta a sec 2 theta d theta 6pt amp a 2 int sec 3 theta d theta 6pt end aligned kullanilarak hesaplanabilir Sonuc olarak a2 x2dx a22 sec 8tan 8 ln sec 8 tan 8 C a22 1 x2a2 xa ln 1 x2a2 xa C 12 xa2 x2 a2ln x a2 x2a C displaystyle begin aligned int sqrt a 2 x 2 dx amp frac a 2 2 sec theta tan theta ln sec theta tan theta C 6pt amp frac a 2 2 left sqrt 1 frac x 2 a 2 cdot frac x a ln left sqrt 1 frac x 2 a 2 frac x a right right C 6pt amp frac 1 2 left x sqrt a 2 x 2 a 2 ln left frac x sqrt a 2 x 2 a right right C end aligned Durum III x2 a2 iceren integrallerx asec 8 displaystyle x a sec theta olsun ve sec2 8 1 tan2 8 displaystyle sec 2 theta 1 tan 2 theta ozdesligini kullanin Durum III icin ornekler Durum III icin geometrik yapi dxx2 a2 displaystyle int frac dx x 2 a 2 seklindeki integraller trigonometrik ikameler yerine ile de hesaplanabilir Bununla birlikte x2 a2dx displaystyle int sqrt x 2 a 2 dx integrali hesaplanamaz Bu durumda uygun bir ikame sudur x asec 8 dx asec 8tan 8d8 8 arcsec xa displaystyle x a sec theta dx a sec theta tan theta d theta theta operatorname arcsec frac x a burada a gt 0 displaystyle a gt 0 boylece a2 a displaystyle sqrt a 2 a ve x gt 0 displaystyle x gt 0 varsayimiyla 0 8 lt p2 displaystyle 0 leq theta lt frac pi 2 olur boylece tan 8 0 displaystyle tan theta geq 0 ve tan2 8 tan 8 displaystyle sqrt tan 2 theta tan theta olur Oyleyse x2 a2dx a2sec2 8 a2 asec 8tan 8d8 a2 sec2 8 1 asec 8tan 8d8 a2tan2 8 asec 8tan 8d8 a2sec 8tan2 8d8 a2 sec 8 sec2 8 1 d8 a2 sec3 8 sec 8 d8 displaystyle begin aligned int sqrt x 2 a 2 dx amp int sqrt a 2 sec 2 theta a 2 cdot a sec theta tan theta d theta amp int sqrt a 2 sec 2 theta 1 cdot a sec theta tan theta d theta amp int sqrt a 2 tan 2 theta cdot a sec theta tan theta d theta amp int a 2 sec theta tan 2 theta d theta amp a 2 int sec theta sec 2 theta 1 d theta amp a 2 int sec 3 theta sec theta d theta end aligned Pay ve paydayi sec 8 tan 8 displaystyle sec theta tan theta ile carparak ve parcalarla hesaplanabilir Sonuc olarak x2 a2dx a22 sec 8tan 8 ln sec 8 tan 8 a2ln sec 8 tan 8 C a22 sec 8tan 8 ln sec 8 tan 8 C a22 xa x2a2 1 ln xa x2a2 1 C 12 xx2 a2 a2ln x x2 a2a C displaystyle begin aligned int sqrt x 2 a 2 dx amp frac a 2 2 sec theta tan theta ln sec theta tan theta a 2 ln sec theta tan theta C 6pt amp frac a 2 2 sec theta tan theta ln sec theta tan theta C 6pt amp frac a 2 2 left frac x a cdot sqrt frac x 2 a 2 1 ln left frac x a sqrt frac x 2 a 2 1 right right C 6pt amp frac 1 2 left x sqrt x 2 a 2 a 2 ln left frac x sqrt x 2 a 2 a right right C end aligned p2 lt 8 p displaystyle frac pi 2 lt theta leq pi oldugunda ki bu da x lt 0 displaystyle x lt 0 oldugunda olur tan 8 0 displaystyle tan theta leq 0 bu durumda da tan2 8 tan 8 displaystyle sqrt tan 2 theta tan theta anlamina gelir Trigonometrik fonksiyonlari ortadan kaldiran ikamelerTrigonometrik fonksiyonlari yok etmek icin ikame kullanilabilir Ornegin f sin x cos x dx 1 1 u2f u 1 u2 duu sin x f sin x cos x dx 1 1 u2f 1 u2 u duu cos x f sin x cos x dx 21 u2f 2u1 u2 1 u21 u2 duu tan x2 displaystyle begin aligned int f sin x cos x dx amp int frac 1 pm sqrt 1 u 2 f left u pm sqrt 1 u 2 right du amp amp u sin x 6pt int f sin x cos x dx amp int frac 1 mp sqrt 1 u 2 f left pm sqrt 1 u 2 u right du amp amp u cos x 6pt int f sin x cos x dx amp int frac 2 1 u 2 f left frac 2u 1 u 2 frac 1 u 2 1 u 2 right du amp amp u tan left frac x 2 right 6pt end aligned Son ikame olarak bilinir ve kullanir Ornegin 4cos x 1 cos x 3dx 21 u24 1 u21 u2 1 1 u21 u2 3du 1 u2 1 u2 du 1 u4 du u u55 C tan x2 15tan5 x2 C displaystyle begin aligned int frac 4 cos x 1 cos x 3 dx amp int frac 2 1 u 2 frac 4 left frac 1 u 2 1 u 2 right left 1 frac 1 u 2 1 u 2 right 3 du int 1 u 2 1 u 2 du amp int 1 u 4 du u frac u 5 5 C tan frac x 2 frac 1 5 tan 5 frac x 2 C end aligned Hiperbolik yerine koymaIntegralleri basitlestirmek icin hiperbolik fonksiyonlarin ikameleri de kullanilabilir Ornegin 1 a2 x2 displaystyle 1 sqrt a 2 x 2 integralini almak icin x asinh u displaystyle x a sinh u ve dolayisiyla dx acosh udu displaystyle dx a cosh u du ikamesini ardindan cosh2 x sinh2 x 1 displaystyle cosh 2 x sinh 2 x 1 ozdesligini kullanin dxa2 x2 acosh udua2 a2sinh2 u cosh udu1 sinh2 u cosh ucosh udu u C sinh 1 xa C displaystyle begin aligned int frac dx sqrt a 2 x 2 amp int frac a cosh u du sqrt a 2 a 2 sinh 2 u 6pt amp int frac cosh u du sqrt 1 sinh 2 u 6pt amp int frac cosh u cosh u du 6pt amp u C 6pt amp sinh 1 frac x a C end aligned Istenirse bu sonuc baska ozdeslikler kullanilarak da donusturulebilir ornegin bagintisini sinh 1 xa C ln xa x2a2 1 C ln x x2 a2a C displaystyle begin aligned sinh 1 frac x a C amp ln left frac x a sqrt frac x 2 a 2 1 right C 6pt amp ln left frac x sqrt x 2 a 2 a right C end aligned Ayrica bakinizVikiversite deTrigonometrik yerine koyma ile ilgili kaynaklar bulunur Vikikitap Vikikitapta bu konu hakkinda daha fazla bilgi var Calculus Integration techniques Trigonometric Substitution Weierstrass ikamesi veya Tanjant yarim aci ikamesi Euler ikamesi Kaynakca 2008 Calculus Early Transcendentals 6 ISBN 978 0 495 01166 8 Weir Maurice D 2010 Thomas Calculus Early Transcendentals 12 Addison Wesley ISBN 978 0 321 58876 0 2012 Section 7 2 Trigonometric Integrals Calculus Early Transcendentals United States Cengage Learning ss 475 6 ISBN 978 0 538 49790 9 Boyadzhiev Khristo N Hyperbolic Substitutions for Integrals PDF 26 Subat 2020 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 4 Mart 2013
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
