Matematik'te, özellikle de cebirde, François Viète'nin adıyla anılan Viète'nin formülleri, bir polinomun kökleriyle katsayıları arasındaki ilişkiyi veren formüllerdir.
Vieta formülleri
Eğer
derecesi 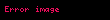


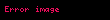



Anlamı, 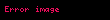


şeklinde her 
İkinci dereceden bir bilinmeyenli cebirsel bir denklemin kökleri ve katsayıları arasındaki ilişki
İkinci dereceden bir bilinmeyenli denklemler genel olarak 



Bu denklemlerden ilki P nin minimum ya da maksimum değerlerini bulmada kullanılabilir.
Vieta formüllerinin ispatı
Viète'nin Formülleri aşağıdaki eşitliği yazıp, polinomların eşitliği kullanılarak gösterilebilir: 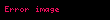
(

Ayrıca bakınız
- Cebirsel Denklem Çözümleri ve Vieta Formülleri[]
- en:Viete (İngilizce)
- en:Second Degree Polynomial (İngilizce)
- en:Rational root theorem (İngilizce)
- en:Fundamental theorem of algebra (İngilizce)
Kaynakça
- Erzen, Ömer R. (2008). Cebirsel Bir Denklemin Kökleriyle Katsayıları Arasındaki Iliskinin Incelenmesi, 19 sf., Çukurova Üniversitesi, Adana.
- Vinberg, E. B. (2003). A course in algebra. American Mathematical Society, Providence, R.I.
- Djukić, Dušan, et al. (2006). The IMO compendium: a collection of problems suggested for the International Mathematical Olympiads, 1959-2004. Springer, New York, NY.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik te ozellikle de cebirde Francois Viete nin adiyla anilan Viete nin formulleri bir polinomun kokleriyle katsayilari arasindaki iliskiyi veren formullerdir Vieta formulleriEger P X anXn an 1Xn 1 a1X a0 displaystyle P X a n X n a n 1 X n 1 cdots a 1 X a 0 derecesi n 1 displaystyle n geq 1 olacak sekilde bir polinom ve bu polinomun katsayilari karmasik sayilardan olusuyorsa yani a0 a1 an 1 an displaystyle a 0 a 1 dots a n 1 a n sayilari kompleks ve an displaystyle a n sifirdan farkli Cebirin Temel Teoremi ne gore P X displaystyle P X n displaystyle n farkli ya da cakisik karmasik koke sahiptir bu kokler x1 x2 xn displaystyle x 1 x 2 dots x n Bu kokler ve katsayilar arasindaki Viete Formulleri asagidaki gibidir x1 x2 xn 1 xn an 1an x1x2 x1x3 x1xn x2x3 x2x4 x2xn xn 1xn an 2an x1x2 xn 1 na0an displaystyle begin cases x 1 x 2 dots x n 1 x n tfrac a n 1 a n x 1 x 2 x 1 x 3 cdots x 1 x n x 2 x 3 x 2 x 4 cdots x 2 x n cdots x n 1 x n frac a n 2 a n vdots x 1 x 2 dots x n 1 n tfrac a 0 a n end cases Anlami P X displaystyle P X in k displaystyle k tane farkli koklerinin olusturdugu tum altkumelerinin carpimi 1 kan k an displaystyle 1 k a n k a n ya esittir diger bir deyisle koklerin olusturdugu her altkumenin bir defa kullanilmasinin garantilemek icin carpimlarini artan indise gore siralayarak 1 i1 lt i2 lt lt ik nxi1xi2 xik 1 kan kan displaystyle sum 1 leq i 1 lt i 2 lt cdots lt i k leq n x i 1 x i 2 cdots x i k 1 k frac a n k a n seklinde her k 1 2 n displaystyle k 1 2 dots n yazabiliriz Ikinci dereceden bir bilinmeyenli cebirsel bir denklemin kokleri ve katsayilari arasindaki iliskiIkinci dereceden bir bilinmeyenli denklemler genel olarak P X aX2 bX c displaystyle P X aX 2 bX c seklinde ifade edilebilir Vieta ya gore P X 0 displaystyle P X 0 denkleminin kokleri x1 displaystyle x 1 ve x2 displaystyle x 2 icin kokler toplami ve kokler carpimi asagidaki kurallari saglamaktadir x1 x2 ba x1x2 ca displaystyle x 1 x 2 frac b a quad x 1 x 2 frac c a Bu denklemlerden ilki P nin minimum ya da maksimum degerlerini bulmada kullanilabilir Vieta formullerinin ispatiViete nin Formulleri asagidaki esitligi yazip polinomlarin esitligi kullanilarak gosterilebilir anXn an 1Xn 1 a1X a0 an X x1 X x2 X xn displaystyle a n X n a n 1 X n 1 cdots a 1 X a 0 a n X x 1 X x 2 cdots X x n x1 x2 xn displaystyle x 1 x 2 dots x n bu polinomun kokleri oldugu icin denklemin sagindaki ifade dogrudur sag taraftaki ifadeleri carpi X displaystyle X in ayni dereceli terimlerini bir araya toplayarak gosterebilir Ayrica bakinizCebirsel Denklem Cozumleri ve Vieta Formulleri olu kirik baglanti en Viete Ingilizce en Second Degree Polynomial Ingilizce en Rational root theorem Ingilizce en Fundamental theorem of algebra Ingilizce KaynakcaErzen Omer R 2008 Cebirsel Bir Denklemin Kokleriyle Katsayilari Arasindaki Iliskinin Incelenmesi 19 sf Cukurova Universitesi Adana Vinberg E B 2003 A course in algebra American Mathematical Society Providence R I Djukic Dusan et al 2006 The IMO compendium a collection of problems suggested for the International Mathematical Olympiads 1959 2004 Springer New York NY
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans


