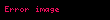Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S1; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x,y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.
Bir birim çember örneklemesidir. t değeri ölçülen açının değerine eşittir.

Bütün x değerleri için x² = (−x)² olduğu için, birim çember üzerinde x ve y eksenlerinin herhangi bir noktası yine birim çember üzerindedir. Yalnızca birinci bölgedeki değil, birim çember üzerinde alınan bütün noktalar(x,y) bu denklemi sağlamaktadır. Ayrıca, diğer diğer birim çemberleri tanımlamak için farklı uzaklık kavramları da kullanılabilir; Rieman çemberi gibi. Fazladan örnekler için matematik standartlarındaki başlıklara bakabilirsiniz.
Karmaşık düzlemlerde
Birim çember, karmaşık sayıların temeli olarak düşünülebilir.
Bu formül Euler eşitliğidir.
Birim çemberde trigonometrik fonksiyonlar
Bir trigonometrik fonksiyon olan kosinüs and sinüs birim çember üzerinde tanımlanabilir. (x,y) birim çember üzerinde bir nokta olsun, orijin(0,0) ve (x,y) arasında oluşturulan çizgi pozitif x ekseninden bir t açısı oluşturur(saat yönünün tersinde döndüğünde pozitif yöndedir).


Bu denklem x2 + y2 = 1 şu bağıntıyı verir:
Birim çember ayrıca sinüs ve kosinüs fonksiyonlarının periyodik fonksiyon olduklarını da gösterir,
Herhangi bir k tam sayısı için. Birim çember üzerinde kurulan üçgenler de trigonometrik fonksiyonların periyodikliğini göstermek için kullanılabilir. Birim çember üzerinde seçilen bir P(x,y) noktası originle QA yarıçapını oluşturmaktadır ve pozitif x ekseni kolunda bir t açısına 0 < t < π/2 sahiptir. Şimdi bir Q(x1,0) noktası düşünün, kesişimleri PQ 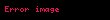
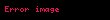

Çember grubu
Kompleks sayılar Öklid düzlemi üzerindeki noktalar ile tespit edilebilir.Yani, a + bi sayısı (a, b) noktası olarak tanımlanabilir. Bu tanımlama altında, birim çember, çember grubu diye bilinen çarpmanın altında bir gruptur. Düzlemde çarpma 
Karmaşık düzlemlerde

Julia seti ve ayrık olmayan dinamik sistemi ile evrim fonksiyonu :
Bu bir birim çemberdir. Bu, yaygın olarak dinamik sistemlerin çalışmasında kullanılan çok basit bir durumdur.
Dış bağlantılar

| Vikisözlük'te unit circle ile ilgili tanım bulabilirsiniz. |
- Eric W. Weisstein, Unit circle (MathWorld)
- Flash animation for learning the unit circle 4 Mayıs 2021 tarihinde Wayback Machine sitesinde .
- : Visualization of the unit circle, trigonometric and hyperbolic function
Kaynakça
- İngilizce vikipedi24 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Birim cember Matematikte yaricapi bir birim olan cembere birim cember denir Cogunlukla ozellikle trigonometride Oklid duzlemine gore Kartezyen koordinat sisteminde merkezi orijin uzerinde 0 0 olan ve yaricapi bir birim olan cemberdir n birim cember siklikla S1 olarak ifade edilir Genellikle daha buyuk boyutlari ise birim kuredir x y birim cember uzerinde bir nokta oldugunda x ve y dik olan ve hipotenusu bir olan ucgenin diger kenar uzunluklaridir Bu nedenle Pisagor teoremine gore x ve y bu denklemi karsilamaktadir x2 y2 1 displaystyle x 2 y 2 1 Bir birim cember orneklemesidir t degeri olculen acinin degerine esittir bir birim cemberin cizimi degiskeni tolan bir aci olcer Butun x degerleri icin x x oldugu icin birim cember uzerinde x ve y eksenlerinin herhangi bir noktasi yine birim cember uzerindedir Yalnizca birinci bolgedeki degil birim cember uzerinde alinan butun noktalar x y bu denklemi saglamaktadir Ayrica diger diger birim cemberleri tanimlamak icin farkli uzaklik kavramlari da kullanilabilir Rieman cemberi gibi Fazladan ornekler icin matematik standartlarindaki basliklara bakabilirsiniz Karmasik duzlemlerdeBirim cember karmasik sayilarin temeli olarak dusunulebilir z eit cos t isin t displaystyle z mathrm e it cos t i sin t Bu formul Euler esitligidir Birim cemberde trigonometrik fonksiyonlarBir trigonometrik fonksiyon olan kosinus and sinus birim cember uzerinde tanimlanabilir x y birim cember uzerinde bir nokta olsun orijin 0 0 ve x y arasinda olusturulan cizgi pozitif x ekseninden bir t acisi olusturur saat yonunun tersinde dondugunde pozitif yondedir acisi8 olan butun trigonometrik fonksiyonlar merkezi 0 olan birim cember geometrik olarak olusturulabilir birim cemberde sinus fonksiyonu ve grafigi cos t x displaystyle cos t x sin t y displaystyle sin t y Bu denklem x2 y2 1 su bagintiyi verir cos2 t sin2 t 1 displaystyle cos 2 t sin 2 t 1 Birim cember ayrica sinus ve kosinus fonksiyonlarinin periyodik fonksiyon olduklarini da gosterir cos t cos 2pk t displaystyle cos t cos 2 pi k t sin t sin 2pk t displaystyle sin t sin 2 pi k t Herhangi bir k tam sayisi icin Birim cember uzerinde kurulan ucgenler de trigonometrik fonksiyonlarin periyodikligini gostermek icin kullanilabilir Birim cember uzerinde secilen bir P x y noktasi originle QA yaricapini olusturmaktadir ve pozitif x ekseni kolunda bir t acisina 0 lt t lt p 2 sahiptir Simdi bir Q x1 0 noktasi dusunun kesisimleri PQ displaystyle perp OQ Sonuc bir dik ucgendir DOPQ ile QOP t Cunku PQ y1 uzunluguna OQ x1 uzunluguna ve QA nin uzunlugu 1 dir sin t y1 and cos t x1 Bu esdegerligini kuran OR yaricapli ayni acili cember uzerinde bir nokta olan R x1 y1 x ekseninin negatif kolundadir Simdi bir nokta dusunun S x1 0 ve kesisimleri RS displaystyle perp OS Sonuc bir dik ucgendir DORS ile SOR t Bu bu nedenle gorulebilir cunku ROQ p t R cos p t noktasi sin p t ayni yontemle P cos t sin t noktasidir Bunun sonucu olarak x1 y1 ifadesi cos p t sin p t ifadesine ve x1 y1 ifadesi de cos t sin t bu ifadeye denktir Bu dogru sin t sin p t ve cos t cos p t Bu benzer bir tarzla anlamlandirilabilir tan p t tan t bu yuzden tan t y1 x1 and tan p t y1 x1 Yukaridaki basit gosterim bir denklemde gorulebilir sin p 4 sin 3p 4 1 sqrt 2 Dik bir ucgen sinus kosinus ve diger trigonometrik fonksiyonlarla calisildiginda yalnizca 0 dan buyuk p 2 den kucuk olan acilar anlamlandirilabilir Ancak birim cember ile tanimlanmis bu islevler icin olculen acisi 2p den buyuk olanlarda bile bu gercek degerleri elde etmek mumkundur Aslinda alti standart trigonometrik fonksiyonlar sinus kosinus tanjant kotanjant sekant kosecant gibi arkaik fonksiyonlari versine ve exsecant sagda gosterildigi gibi bir birim cemberin acisindan geometrik olarak tanimlanabilir Birim cember kullanarak bircok aci icin herhangi bir trigonometrik fonksiyon degeri toplam ve fark formullerini kullanarak bir hesap makinesi kullanmadan hesaplanabilir birim cember belirli noktalarin koordinatlariniCember grubuKompleks sayilar Oklid duzlemi uzerindeki noktalar ile tespit edilebilir Yani a bi sayisi a b noktasi olarak tanimlanabilir Bu tanimlama altinda birim cember cember grubu diye bilinen carpmanin altinda bir gruptur Duzlemde carpma cos 8 isin 8 displaystyle cos theta i sin theta amp theta acisiyla saat yonunun tersinde bir donme olusturur Bu grup matematikte ve bilimde onemli uygulamalara sahiptir Karmasik duzlemlerdekompleks dinamiklerde birim cember Julia seti ve ayrik olmayan dinamik sistemi ile evrim fonksiyonu f0 x x2 displaystyle f 0 x x 2 Bu bir birim cemberdir Bu yaygin olarak dinamik sistemlerin calismasinda kullanilan cok basit bir durumdur Dis baglantilarVikikitap Vikikitapta bu konu hakkinda daha fazla bilgi var Trigonometry The unit circle Vikisozluk te unit circle ile ilgili tanim bulabilirsiniz Eric W Weisstein Unit circle MathWorld Flash animation for learning the unit circle 4 Mayis 2021 tarihinde Wayback Machine sitesinde Visualization of the unit circle trigonometric and hyperbolic functionKaynakcaIngilizce vikipedi24 Ekim 2014 tarihinde Wayback Machine sitesinde arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans