Binom opsiyon fiyatlama modeli

Finansta ve matematiksel finansta binom modeli ya da Cox-Ross-Rubinstein modeli, opsiyon ya da türev ürünlerini fiyatlamada kullanılan nümerik bir yönteme verilen addır. Model, opsiyonların dayanak varlığının değişen fiyatlarının kesikli-zamana (latis bazlı) uyarlanması sonucu oluşan bir modeldir.

Binom modeli, ilk başta William Sharpe'ın Investments adlı kitabında yer almıştır. Yaklaşık aynı zamanda, , ve 'ın 1979'daki makalesinde daha esaslı bir sistemde sunulmuştur. Yine aynı yılda, Rendleman ve Bartter'ın da bu konuda bir çalışması vardır.

Kullanımı

Binom modeli, bir opsiyonun ya da türev ürününün dayanak varlığının fiyatını türev ürünün vadesine kadar göz önüne aldığı için, değişik türdeki türev ürünlerini fiyatlamayı mümkün kılar. Mesela, (Amerikan tipi opsiyonlar) ya da (Bermuda tipi opsiyonların) alıcıları sözleşmeden doğan haklarını ürünün vadesine kadar herhangi bir zamanda ya da önceden belirlenmiş belli tarihlerde kullanabilecekleri için, binom modeli bu ürünleri fiyatlandırmayı mümkün kılar. Ancak türev ürünlerinin sözleşme detayları karmaşıklaştıkça, binom modelinin uygulanabilme özelliği azalır. Bunun nedeni ise, Monte Carlo simülasyonu ve sonlu fark yöntemleri gibi diğer nümerik yöntemlerin opsiyon fiyatlarının ve risk hassasiyetlerinin hesaplanması hızı konusunda binom modelinden daha fazla önce çıkmalarıdır. Mesela, binom modelinin zaman karmaşıklığı en kötü ihtimalle ${\displaystyle O(2^{n})}$ olabilir. Buna karşılık, Monte-Carlo simülasyonu genelde polinom zaman karmaşıklığına sahiptir ve simülasyon sayısı arttığında daha hızlı olacaktır.

Modelin yöntemi

Binom modelindeki binom ağacı (Cox-Ross-Rubinstein)

def Amerikan(T,S0, K, r, sig, N, opsiyon): dT = float(T) / N # Delta t u = np.exp(sig * np.sqrt(dT)) # yukarı olasılık d = 1.0 / u # aşağı olasılık # fiyat vektörü V = np.zeros(N + 1) # S_T'nin T zamanındaki değeri S_T = np.array([(S0 * u**j * d ** (N - j)) for j in range(N + 1)]) a = np.exp(r * dT) # risksiz faiz oranı p = (a - d) / (u - d) # riske duyarsız yukarı olasılık q = 1.0 - p # riske duyarsız aşağı olasılık if opsiyon== "alim": V[:] = np.maximum(S_T - K, 0.0) elif payoff == "satim": V[:] = np.maximum(K - S_T, 0.0) for i in range(N - 1, -1, -1): # fiyatların her adımda ustune yazıyoruz V[:-1] = np.exp(-r * dT) * (p * V[1:] + q * V[:-1]) # bir önceki adımdaki fiyat S_T = S_T * u if opsiyon== "alim": V = np.maximum(V, S_T - K) elif payoff == "satim": V = np.maximum(V, K - S_T) return V[0] }

Binom modeli türev ürününün en bariz değişkenlerinin gelecekteki değerlerini kesikli zamanlarda modelleyerek ortaya olası değerler çıkarır ve bu veriler üzerinden türev ürününü fiyatlandırır. Bunu yapmak için, fiyatlama yapılan günden türev ürünün vadesine kadar olan zaman diliminde değişik tarihleri vermek üzere zaman adımları belirlenir. İlk günden başlayarak ve her bir zaman adımı sırasıyla kullanılarak, dayanak varlığın bir sonraki adımdaki olası fiyatları belirlenir. Her bir sonraki adım, bir önceki zaman adımındaki olası fiyatları (ya da diğer değişken değerleri) kullanarak yine olası fiyatlar belirler. Böylece, fiyatlama gününden vade zamanına kadar olan zaman diliminde, her bir zaman adımında olası fiyatlar belirlenmiş olur. Ortaya çıkan ağaç benzeri bu yapıya binom ağacı ya da binom latisi denir ve her zaman adımına karşık gelen olası fiyatlar da birer düğüm noktası olur. Eğer dayanak varlığın dışında başka değişkenler de modellenecekse, onlar için de bu binom ağacındaki değerlere bağlı ya da bu değerlerden bağımsız hesap edilen binom ağaçları da inşa edilir.

Tüm olası fiyatlar belirlendiğinde, bu sefer türev ürününün fiyatlandırılması vadedeki olası fiyatlardan başlayarak ve fiyat yapılan güne doğru geri yönlü giderek yapılır. Bu halde, vadedeki düğüm noktalarında her düğüme karşılık gelen bir opsiyon fiyatı elde edilir ve bu fiyatlardan bir önceki zaman aralığındaki düğüm noktalarındaki opsiyon fiyatları ortaya çıkarılır.

Özet olarak, binom modelinin kurulumu şu üç adımdan oluşur.

1. Binom ağacı oluşturma
2. Vadededeki düğüm noktalarında türev ürününün fiyatını bulma
3. Daha önceki düğüm noktalarında bir sonraki düğüm noktalarında elde edilen opsiyon fiyatlarından yeni opsiyon fiyatları elde etme.

Adım 1: Binom ağacı oluşturma

Binom ağacını oluşturmak için bugünden vadeye kadar zaman adımları belirlenir. Her adımda, dayanak varlığın fiyatının ya aşağıya ya da yukarıya gideceği varsayılır. Mesela, eğer bir düğüm noktasındaki fiyat ${\displaystyle S}$ ise buradan bir sonraki adımdaki fiyatların, ${\displaystyle 0<d\leq 1}$ ve ${\displaystyle u\geq 1}$ olmak üzere ${\displaystyle S_{asa}:=S\cdot d}$ ve ${\displaystyle S_{yuk}:=S\cdot u}$ olacağı hesaplanır. Burada, ${\displaystyle u}$ ve ${\displaystyle d}$ çarpanları dayanak varlığın oynaklığı ${\displaystyle \sigma }$ ve bir önceki zamandan bir sonraki zamana kadar olan geçen zaman aralığı olan ${\displaystyle \Delta t}$'nın yıl olarak temsiline (sözleşmedeki gün sayma uzlaşımı kullanılarak) bağlıdır. Mesela, Cox, Ross ve Rubinstein modeli özelinde, eşit zaman aralıkları alınarak,

${\displaystyle u=e^{\sigma {\sqrt {\Delta t}}}}$

${\displaystyle d=e^{-\sigma {\sqrt {\Delta t}}}={\frac {1}{u}}}$

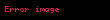
tanımlanır ve böylelikle binom ağacının rekombinant yani tekrar birleşen özelliği garanti edilir. Diğer deyişle, bir dayanak varlığın fiyatı bir adımda ilk önce yukarı sonra da aşağı gidiyorsa, en son hesaplanan fiyat yine bu dayanak varlığın ilk önce aşağı sonra da yukarı gideceği durumda en son hesaplanan fiyatla eşit olacaktır. Elbette, buradaki binom ağacını daha genel tekniklere müsaade edecek şekilde geliştirecek binom ağacı modelleri de vardır ya da bir latisi farklı tekniklerle (eşit olasılık teknikleri gibi) üretebilecek yöntemler de mevcuttur. Ancak, Cox, Ross ve Rubinstein modelindeki varsayımlar binom ağacındaki düğüm sayısını azaltıp hesaplama hızının önünü de açar. Aslında, Cox, Ross ve Rubinstein modelinde, her bir düğüm noktasına ne kadar yukarı (${\displaystyle N_{u}}$) ve ne kadar aşağı (${\displaystyle N_{d}}$) yönlü hareket yapılarak bilindiği için, binom ağacını oluşturmaya bile gerek kalmaz. Bu model özelinde, ${\displaystyle n}$'inci düğüm noktasında ${\displaystyle S_{n}=S_{0}u^{N_{u}-N_{d}}}$ olacaktır.

Adım 2: Vadedeki düğüm noktalarında türev ürününün fiyatını bulma

En son adıma denk gelen her bir düğümde; yani, türevin vadesine karşık gelen her düğüm noktasında ödeniş fonkiyonu kullanılarak opsiyonun değeri bulunur. Hesap vadede yapıldığı için burada yapılan vadedeki hesabından başkası değildir. Mesela, kullanım fiyatı ${\displaystyle K}$ ve dayanak varlığının ${\displaystyle n}$'inci zamanda ${\displaystyle S_{n}}$ olan Avrupa tipi bir alım ya da satım opsiyonu için

[ (S_n− K), 0 ], ${\displaystyle \quad }$ alım opsiyonu

Max [ (K − S_n), 0 ], ${\displaystyle \quad }$ satım opsiyonu

hesaplanır.

Adım 3: Daha önceki düğüm noktalarında opsiyon fiyatlarını hesaplama

Bir önceki adım tamamlandığında, vadeye denk gelen düğümlerdeki opsiyon fiyatlarından başlayarak vadeden bir önceki zamana denk gelen düğüm noktalarındaki opsiyon fiyatları elde edilir. Aynı yöntem, fiyatlama gününe denk gelen düğüme kadar tekrarlanıp opsiyonun fiyatlama günündeki fiyatı elde edilir. Bu yöntemi uygulamak için varlığı varsayılır. Bu varsayım altında, beklenen değerin iskontolu hali bugünkü fiyatı verecektir. Bu sebeple ilk önce bu bağlantıdan fiyatların yukarı ve aşağıya gitme olasılıklarını belirleyen ${\displaystyle p}$ olasılık değeri bulunur. Diğer deyişle,

${\displaystyle S=({\text{İskonto}})(pS_{yuk}+(1-p)S_{asa})=({\text{İskonto}})(pSu+(1-p)Sd)\implies p={\frac {\left({\frac {1}{\text{İskonto}}}\right)-d}{u-d}}}$

elde edilir. Ancak burada bir koşula dikkat edilmelidir. ${\displaystyle p}$ bir olasılık değeri olacağı için, bu modelde değerlerini ${\displaystyle (0,1)}$ aralığında alır. O zaman,

${\displaystyle {\frac {\left({\frac {1}{\text{İskonto}}}\right)-d}{u-d}}<1\implies {\text{İskonto}}>e^{-\sigma {\sqrt {\Delta t}}}}$

olur. Eğer ${\displaystyle {\text{İskonto}}=e^{-r{\sqrt {\Delta t}}}}$ alınırsa, yukarıdaki eşitsizlikten ${\displaystyle \Delta t<{\frac {\sigma ^{2}}{r^{2}}}}$ şartı elde edilir. Ayrıca, ${\displaystyle {\text{İskonto}}=e^{-r{\sqrt {\Delta t}}}}$ ise,

${\displaystyle e^{-r{\sqrt {\Delta t}}}p=e^{-r{\sqrt {\Delta t}}}\left({\frac {e^{r\Delta t}-d}{u-d}}\right)=e^{-r{\sqrt {\Delta t}}}\left({\frac {ue^{r\Delta t}-1}{u^{2}-1}}\right)={\frac {u-e^{-r\Delta t}}{u^{2}-1}}}$

${\displaystyle e^{-r{\sqrt {\Delta t}}}(1-p)=e^{-r{\sqrt {\Delta t}}}-e^{-r{\sqrt {\Delta t}}}p=e^{-r{\sqrt {\Delta t}}}-{\frac {u-e^{-r\Delta t}}{u^{2}-1}}={\frac {u^{2}e^{-r{\sqrt {\Delta t}}}-u}{u^{2}-1}}}$

olur. Olasılık değeri ${\displaystyle p}$ hesaplandıktan sonra, bir düğüm noktasındaki adil opsiyon fiyatı hesplanır. Yani, dayanak varlığının yukarı ve aşağı yönlü hareketine karşılık gelen değerleri bir sonraki düğüm noktasında ${\displaystyle C_{yuk}}$ ve ${\displaystyle C_{asa}}$ ise, bu fiyatlardan bir önceki düğüm noktasındaki adil opsiyon değeri

${\displaystyle C=({\text{İskonto}})(pC_{yuk}+(1-p)C_{asa})}$

olarak bulunur. Bulunan bu değer Binom değeridir ve her bir düğüm noktasında bir dayanak varlık fiyatına karşılık gelen adil bir opsiyon fiyatıdır. Diğer deyişle bu fiyat değeri opsiyon hakları kullanılmadığı zaman elde edilen fiyatı tensil etmektedir. O yüzden, bir sonraki aşama, opsiyon türüne göre Binom değerinin kullanılıp kullanılmayacağına karar vermektir:

• Avrupa tipi opsiyon: Erken hak kullanımı yoktur, bu yüzden binom değeri bütün düğüm noktalarında geçerlidir.
• Amerikan tipi opsiyon: Erken hak kullanımı her düğüm noktasında mümkün olabilir. O zaman, her düğüm noktasındaki opsiyon fiyatı binom değeri ile hak kullanımından elde edilen değerin büyüğüdür.
• Bermuda tipi opsiyon: Erken hak kullanımı sadece sözleşmede belirlenen tarihlerde mümküdür. O zaman, sadce bu tarihlere karşılık gelen düğüm noktalarında opsiyon fiyatı binom değeri ile hak kullanımından elde edilen değerin büyüğüdür. Diğer tarihlerde, yine binom değeridir.

Hesaplanan bir zaman adımındaki opsiyon değeri hesaplamada (yani değerlemeye bir adım daha yakın) düğüm noktasında, daha sonraki düğümlerden ${\displaystyle C_{yuk}}$ ve ${\displaystyle C_{asa}}$ değerlerinden doğru olanını kullanmalıdır. Sağ taraftaki Python kurulumu, bir Amerikan alım ya da satım opsiyonunun fiyatını hesaplama yaklaşımını göstermektedir (temettüler yok sayılmıştır). Bu algoritmayı Avrupa ve Bermuda opsiyonları için geliştirmek de mümkündür.

Black-Scholes ile ilişki

Benzer varsayımlar hem binom modeli hem de Black-Scholes modeli için geçerlidir. Binom modeli, aslında Black-Scholes modelinin modeline kesikli zamanlı bir yaklaşım sağlar. Binom modeli, fiyat hareketlerinin binom dağılımını izlediğini varsayar. Eğer, bu binom dağılımının parameteresi olan ${\displaystyle n}$ deneme sayısı büyük sayılara doğru arttırılırsa, o zaman Black-Scholes tarafından varsayılan log-normal dağılıma yaklaşır. Bu durumda, temettüsüz dayanak varlığı olan Avrupa tipi opsiyonları için, binom modeli değeri zaman adımlarının sayısı arttıkça Black-Scholes formül değerine yakınsar.

Ayrıca bakınız

• Black-Scholes formülü
• Black-Scholes modeli
• Black modeli

Kaynakça

1. ^ William F. Sharpe, Biographical 9 Eylül 2024 tarihinde Wayback Machine sitesinde arşivlendi., nobelprize.org
2. ^ ; ; (1979). "Option pricing: A simplified approach". . 7 (3). s. 229. CiteSeerX 10.1.1.379.7582 $2. doi:10.1016/0304-405X(79)90015-1. 
3. ^ Richard J. Rendleman, Jr. and Brit J. Bartter. 1979. "Two-State Option Pricing". 24: 1093-1110. DOI:10.2307/2327237
4. ^ ^{a b} Mark s. Joshi (2008). The Convergence of Binomial Trees for Pricing the American Put 2 Temmuz 2015 tarihinde Wayback Machine sitesinde arşivlendi.
5. ^ ^{a b} Chance, Don M. March 2008 A Synthesis of Binomial Option Pricing Models for Lognormally Distributed Assets 4 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi.. Journal of Applied Finance, Vol. 18