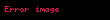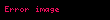Determinant kare bir matris ile ilişkili özel bir sayıdır.
Bir A matrisin determinant'ı det(A) ya da det A şeklinde gösterilir. Diğer bir gösterim şekli ise matrix elementlerini arasına alan dikey çizgi ikilisidir. Örneğin:
- matrisinin determinantı şu şekilde gösterilir: .
Basit bir örnek olarak,
matrisinin determinantı şudur:
Determinantın açık tanımı
Determinantın açık tanımı bir A matrisinin kofaktörü C ya da M cinsinden gösterilebilir:
- .
Determinant ve geometri
Yukarıda belirtilen 2x2 A matrisinin determinantın mutlak değeri, köşeleri (0,0), (a,b), (a + c, b + d) ve (c,d) noktalarında olan bir paralelkenarın alanına eşittir.
Benzer bir şekilde, 3x3 bir matrisin determinantının mutlak değeri, üç boyutlu cisminin hacmine eşittir.
Determinantın temel özellikleri
- Birim matrisin determinantı birdir:
- Iki matrisin çarpımının determinantı, bu iki matrisin determinantlarının çarpımına eşittir:
- .
- det(A) sıfırdan farklı ise, A matrisinin tersi A−1 tanımlıdır. Bu durumda:
- .
- A ve B benzer matrisler olsun: ve dönüşüm matrisi X in tersi tanımlı olsun. Bu durumda:
- .
- Bir matrisin transpozunun determinantı kendi determinantına eşittir:
- .
- Bir matrisin bir sayı ile çarpımının determinantı:
- .
Kalıp Matrisler (Blok matrisler)
Boyutları n×n, n×m, m×n ve m×m olan A, B, C ve D matrislerinin olduğunu varsayalım. Bu matrisleri kullanarak n+m × n+m boyutunda büyük bir kare matris M oluşturalım. M'yi oluşturan A, B, C ya da D kalıplarından herhangi birisi sıfır matris ise, M'nin determinantı kolayca hesaplanabilir:
Bu sonuç M matrisini iki matrisin çarpımı şekilde yazarak kolayca gösterilebilir. Anın tersi tanımlı olsun. Bu durumda
denkliği yazılabilir ve buradan determinant
şeklinde hesaplanır. B ya da Cnin sıfır matris olması durumda yukarıdaki sonucu elde etimiş oluruz.
Ayrıca,
C ve D'nin değişme özelliği var ise, yani CD = DC ise, 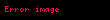
A ve C'nin değişme özelliği var ise, yani AC = CA ise, 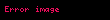
B ve D'nin değişme özelliği var ise, yani BD = DB ise, 
A ve B'nin değişme özelliği var ise, yani AB = BA ise, 
Notlar
- Bu sayfanın içeriği aynı adlı İngilizce makaleden alınmıştır: en:Wikipedia:Determinant
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Determinant kare bir matris ile iliskili ozel bir sayidir Bir A matrisin determinant i det A ya da det A seklinde gosterilir Diger bir gosterim sekli ise matrix elementlerini arasina alan dikey cizgi ikilisidir Ornegin abcdefghi displaystyle begin bmatrix a amp b amp c d amp e amp f g amp h amp i end bmatrix matrisinin determinanti su sekilde gosterilir abcdefghi displaystyle begin vmatrix a amp b amp c d amp e amp f g amp h amp i end vmatrix Basit bir ornek olarak A abcd displaystyle A begin bmatrix a amp b c amp d end bmatrix matrisinin determinanti sudur detA ad bc displaystyle det A ad bc Determinantin acik tanimi Determinantin acik tanimi bir A matrisinin kofaktoru C ya da M cinsinden gosterilebilir det A j 1nAi jCi j j 1nAi j 1 i jMi j displaystyle det A sum j 1 n A i j C i j sum j 1 n A i j 1 i j M i j Determinant ve geometri Yukarida belirtilen 2x2 A matrisinin determinantin mutlak degeri koseleri 0 0 a b a c b d ve c d noktalarinda olan bir paralelkenarin alanina esittir Benzer bir sekilde 3x3 bir matrisin determinantinin mutlak degeri uc boyutlu cisminin hacmine esittir Determinantin temel ozellikleri Birim matrisin determinanti birdir 10 001 0 00 1 1 displaystyle begin vmatrix 1 amp 0 amp ldots amp 0 0 amp 1 amp ldots amp 0 vdots amp vdots amp ddots amp vdots 0 amp 0 amp ldots amp 1 end vmatrix 1 dd Iki matrisin carpiminin determinanti bu iki matrisin determinantlarinin carpimina esittir det AB det A det B displaystyle mathsf det AB det A det B det A sifirdan farkli ise A matrisinin tersi A 1 tanimlidir Bu durumda det A 1 det A 1 displaystyle mathsf det A 1 left det A right 1 A ve B benzer matrisler olsun A X 1BX displaystyle textstyle mathsf A X 1 BX ve donusum matrisi X in tersi X 1 displaystyle textstyle mathsf X 1 tanimli olsun Bu durumda det A det X 1det BX det X 1det B det X det B det X 1det X det B displaystyle mathsf det A det X 1 det BX det X 1 det B det X det B det X 1 det X det B Bir matrisin transpozunun determinanti kendi determinantina esittir det AT det A displaystyle mathsf det A mathrm T det A Bir matrisin bir sayi ile carpiminin determinanti det aA andet A displaystyle mathsf det alpha A alpha n det A Kalip Matrisler Blok matrisler Boyutlari n n n m m n ve m m olan A B C ve D matrislerinin oldugunu varsayalim Bu matrisleri kullanarak n m n m boyutunda buyuk bir kare matris M olusturalim M yi olusturan A B C ya da D kaliplarindan herhangi birisi sifir matris ise M nin determinanti kolayca hesaplanabilir det A0CD det AB0D det A det D displaystyle det begin pmatrix mathsf A amp 0 mathsf C amp mathsf D end pmatrix det begin pmatrix mathsf A amp mathsf B 0 amp mathsf D end pmatrix mathsf det A det D Bu sonuc M matrisini iki matrisin carpimi sekilde yazarak kolayca gosterilebilir Anin tersi tanimli olsun Bu durumda ABCD A0CI IA 1B0D CA 1B displaystyle begin pmatrix mathsf A amp mathsf B mathsf C amp mathsf D end pmatrix begin pmatrix mathsf A amp 0 mathsf C amp mathsf I end pmatrix begin pmatrix mathsf I amp mathsf A 1 mathsf B 0 amp mathsf D CA 1 B end pmatrix denkligi yazilabilir ve buradan determinant det ABCD det A det D CA 1B displaystyle det begin pmatrix mathsf A amp mathsf B mathsf C amp mathsf D end pmatrix mathsf det A det D CA 1 B seklinde hesaplanir B ya da Cnin sifir matris olmasi durumda yukaridaki sonucu elde etimis oluruz Ayrica C ve D nin degisme ozelligi var ise yani CD DC ise det ABCD det AD BC displaystyle det begin pmatrix mathsf A amp mathsf B mathsf C amp mathsf D end pmatrix mathsf det AD BC A ve C nin degisme ozelligi var ise yani AC CA ise det ABCD det AD CB displaystyle det begin pmatrix mathsf A amp mathsf B mathsf C amp mathsf D end pmatrix mathsf det AD CB B ve D nin degisme ozelligi var ise yani BD DB ise det ABCD det DA BC displaystyle det begin pmatrix mathsf A amp mathsf B mathsf C amp mathsf D end pmatrix mathsf det DA BC A ve B nin degisme ozelligi var ise yani AB BA ise det ABCD det DA CB displaystyle det begin pmatrix mathsf A amp mathsf B mathsf C amp mathsf D end pmatrix mathsf det DA CB NotlarBu sayfanin icerigi ayni adli Ingilizce makaleden alinmistir en Wikipedia DeterminantMatematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans