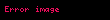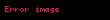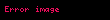Matematikte aşağıda gösterilen özellikleri sağlayan cebir yapısına "alan" denir. Alan sonlu sayıda elemanlardan (noktalardan) oluşursa "Galois" alanı denir. Fizik kuramlarında kullanılan alanlar genellikle sonsuz sayıda nokta içerir. Alan'daki her nokta reel sayı, karmaşık sayı, vektör, tensör, ya da fonksiyon olabilir.
her noktasına karşılık birde noktası vardır ve şu özelliği sağlar:
Değeri olmayan her elemana (noktaya) karşılık vardır ve şu özelliği sağlar:
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte asagida gosterilen ozellikleri saglayan cebir yapisina alan denir Alan sonlu sayida elemanlardan noktalardan olusursa Galois alani denir Fizik kuramlarinda kullanilan alanlar genellikle sonsuz sayida nokta icerir Alan daki her nokta reel sayi karmasik sayi vektor tensor ya da fonksiyon olabilir x y y x displaystyle x y y x x y z x y z displaystyle x y z x y z x 0 x displaystyle x 0 x xy yx displaystyle xy yx xy z x yz displaystyle xy z x yz 1x x displaystyle 1x x x y z xy xz displaystyle x y z xy xz her x displaystyle x noktasina karsilik birde x displaystyle x noktasi vardir ve su ozelligi saglar x x 0 displaystyle x x 0 Degeri 0 displaystyle 0 olmayan her elemana noktaya karsilik 1 x displaystyle 1 x vardir ve su ozelligi saglar x 1 x 1 displaystyle x 1 x 1
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans