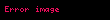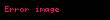sayısına 'a atfen Gelfond sabiti adı verilmiştir; eπe sayısının π'nci kuvvetidir ve aşkın sayıdır.'i ile kanıtlanabilir. bağıntısında i sayısı imajiner kısımdır ve -i'de cebirsel bir sayıdır,ama cebirsel sayılar'dan değildir,yani dandır ve Hilbert'in yedinci teoreminde bahsi geçer. Matematiksel açıdan estetik olan yönü;
- veya
ifadesi ile daha iyi anlaşılabilir.Çünkü eşitliğin bir tarafı tamamen reel'ken diğer tarafı tamamen imajinerdir. (hangisi gerçek?!)
Nümerik değeri
Gelfond sabiti onluk sayı sisteminde açılımında:
olarak tanımlarsak;
için bu dizi[]
şeklinde gösterilebilir.
- bununda limiti
şeklindedir.
Geometrik gariplik
- n-boyutlu kürenin (veya ) hacmi
- şeklinde verilir.
- Birim veya üzeri tüm boyutlardaki kürenin hacmini özetleyen formül
- Birim ve üzerindeki boyutlardaki kürelerin hacimlerinin toplamını veren formül:
Sayısal gariplik

Bazı değerler
eπile πearasındaki ilişki:
Kaynakça
1. ^ Nesterenko, Y (1996). "Modular Functions and Transcendence Problems". Comptes rendus de l'Académie des sciences Série 1 322 (10): 909–914. 2. ^ Connolly, Francis. University of Notre Dame
Dış bağlantılar
- Gelfond's constant at MathWorld21 Ekim 2018 tarihinde Wayback Machine sitesinde .
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
ep 23 14069263277926 displaystyle e pi approx 23 14069263277926 dots sayisina a atfen Gelfond sabiti adi verilmistir epe sayisinin p nci kuvvetidir ve askin sayidir i ile kanitlanabilir ep eip i 1 i displaystyle e pi e i pi i 1 i bagintisinda i sayisi imajiner kisimdir ve i de cebirsel bir sayidir ama ep displaystyle e pi cebirsel sayilar dan degildir yani dandir ve Hilbert in yedinci teoreminde bahsi gecer Matematiksel acidan estetik olan yonu ep i 2i displaystyle e pi i 2i veya ep 2 i i displaystyle e pi 2 i i ifadesi ile daha iyi anlasilabilir Cunku esitligin bir tarafi tamamen reel ken diger tarafi tamamen imajinerdir hangisi gercek Numerik degeriGelfond sabiti onluk sayi sisteminde aciliminda ep 23 14069263277926 displaystyle e pi approx 23 14069263277926 dots k0 12 displaystyle scriptstyle k 0 tfrac 1 sqrt 2 olarak tanimlarsak kn 1 1 kn 121 1 kn 12 displaystyle k n frac 1 sqrt 1 k n 1 2 1 sqrt 1 k n 1 2 n gt 1 displaystyle n gt 1 icin bu dizi kaynak belirtilmeli 4 kn 21 n displaystyle 4 k n 2 1 n seklinde gosterilebilir bununda limiti ep displaystyle e pi seklindedir Geometrik gariplikn boyutlu kurenin veya hacmi Vn pn2RnG n2 1 displaystyle V n pi frac n 2 R n over Gamma frac n 2 1 seklinde verilir Birim veya uzeri tum boyutlardaki kurenin hacmini ozetleyen formul V2n pnn displaystyle V 2n frac pi n n Birim ve uzerindeki boyutlardaki kurelerin hacimlerinin toplamini veren formul n 0 V2n ep displaystyle sum n 0 infty V 2n e pi Sayisal gariplikep p 19 99909997918947 displaystyle e pi pi 19 99909997918947 ldots Bazi degerlerep2 i i 4 81047738096535 displaystyle e frac pi 2 i i approx 4 81047738096535 dots e p2 ii 0 20787957635076 displaystyle e frac pi 2 i i approx 0 20787957635076 dots e p24 e ln i 2 iln i 0 1076929315 displaystyle e frac pi 2 4 e ln i 2 i ln i approx 0 1076929315 dots epile pearasindaki iliski pe eeln p 22 4591577183610454 displaystyle pi e e e ln pi approx 22 4591577183610454 dots eln p 3 111698447198 displaystyle e ln pi approx 3 111698447198 dots p eln p 0 0298942063913 displaystyle pi e ln pi approx 0 0298942063913 dots ep eln p eppe 1 03034552421621 displaystyle e pi e ln pi frac e pi pi e 1 03034552421621 eeln p p peep 0 970548205914423 displaystyle e e ln pi pi frac pi e e pi 0 970548205914423 peep eppe 2 0008937301306 displaystyle frac pi e e pi frac e pi pi e 2 0008937301306 Kaynakca1 Nesterenko Y 1996 Modular Functions and Transcendence Problems Comptes rendus de l Academie des sciences Serie 1 322 10 909 914 2 Connolly Francis University of Notre DameDis baglantilarGelfond s constant at MathWorld21 Ekim 2018 tarihinde Wayback Machine sitesinde Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans