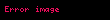Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
SAT problemi bir NP-tam sınıfı problemidir.
Giriş
Teoremin ispatına geçmeden önce teoremin çıkış noktası üzerinde duralım. Polinom zamanda kararlaştırılan problem ( problemleri) ile polinom zamanda doğrulanabilen problem ( problemleri) sınıflarının birbirine denk olup olmadığı güncel matematik ve teorik bilgisayar biliminin bir türlü çözemediği bir sorun olagelmiştir. Eğer bu sınıflar birbirine denk olduğu gösterilirse herhangi polinom zamanda doğrulanabilen bir problemin (NP sınıfı problemi) artık polinom zamanda kararlaştırılabiliyor olacağı kesin olarak söylenmiş olacaktır.
1970’lerde P ve NP sınıflarının arasındaki ilişkiye Stephen Cook ve adındaki iki bilim adamı farklı bir açıdan yaklaşmışlardır; bazı NP sınıfı problemlerinin karmaşıklıklarının tek başlarına tüm NP sınıfının karmaşıklığına eşit olduğunu fark etmişler. Eğer bu tip problemlerin polinom zamanda bir çözümü bulunursa NP sınıfındaki tüm problemler polinom zamanda çözülebilir. Bu tip problemlere ileride değineceğiz ve bun tip problemlere NP-tam sınıfı problemleri diyeceğiz. Dolayısıyla Cook-Levin yaklaşımının bir sonucu olarak P sınıfıyla NP sınıfının eşitliğini iddia eden biri NP-tam bir problemi polinom zamanda çözmesi iddiasını ispatlamak için yeterli olacaktır.
SAT Problemi
SAT (Doğrulanabilirlik) probleminin ne olduğundan bahsedelim. SAT problemi verilen bir boolean ifadenin sonucunun doğru olup olmayacağıyla problemidir. Yani boolean ifadeyi doğru kılacak, boolean ifadenin değişkenlerinin bir “doğru, yanlış” kombinasyonunun oluşturup oluşturmayacağıyla ilgilenir. Dolayısıyla SAT problemi aşağıdaki gibi ifade edilebilir:
Örneğin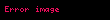 
gibi herhangi bir boolean ifadenin sonucunun doğru olmasını inceleyen probleme SAT problemi denir. Bu örnekte x = doğru, y = yanlış, z = doğru için problem doğrulanabilirdir.
NP-Tam Sınıfı
Bir B dili NP-tam ise şu iki şartı sağlamalıdır:
- B dili NP sınıfındadır.
- NP sınıfındaki her dil B diline polinom zamanda indirgenebilir.
Burada yeni bir kavramla karşılaşıyoruz; “”. Bunu fazla derine inmeden şöyle özetleyebiliriz; eğer bir problemin çözümünü bilmiyorsak ya da çözümü bulmakta çok zorlanıyorsak asıl problemimizi çözmeye yardımcı olacak yeni bir probleme indirgeriz ve çözüme yeni indirgenmiş problem aracılığıyla ulaşırız. Eğer bu indirgememiz polinom zamanda gerçekleştirilirse buna da “polinom zamanda indirgemek” adını veririz. Buna şöyle bir örnek verebiliriz: Bilmediğiniz bir yere gitmek istediğinizi farz edelim ve bu problemin sizin için zor bir problem olduğunu düşünelim. Bu durumda gideceğiniz yere ulaşmak için bir yardımcıya ihtiyacınız olacaktır. Bu yardımcılar taksiye binmek, harita elde etmek ya da bilen birine sormak bunlar arasında sayılabilir. Böylelikle bizim için zor olan problemimiz taksi ya da harita bulmak kadar basit bir probleme indirgenmiş oldu. Kısaca buna da değindikten sonra artık teoremimize dönelim.
İspat
SAT probleminin NP-tam sınıfına ait bir problem olduğunu göstermek için öncelikle SAT dilinin NP sınıfında olduğunu göstermemiz lazım.
SAT probleminin NP sınıfında olduğunu göstermenin iki farklı yolu vardır:
- SAT problemini polinom zamanda doğrulayan bir Turing Makinesi(TM) tasarlamalıyız.
- Ya da SAT problemini polinom zamanda kararlaştıran bir deterministik olmayan Turing Makinesi (NTM) tasarlamalıyız.
Biz burada 2. yolla bunu ispatlayalım: Deterministik olmayan N Turing Makinesi, SAT dilini polinom zamanda aşağıdaki gibi kararlaştırsın:
N: “ ∅ ’nin Boolean ifade, x1, x2, x3,...., xk’nin de bu ifadenin bir değişkeni olsun ve makine girdi olarak < ∅, x1, x2, x3,...., xk > katarını alsın.
- Deterministik olmayacak şekilde boolean ifadedeki değişkenlere “doğru ve yanlış” değerlerini ata.
- Elde edilen kombinasyonla boolean formülün doğru cevap üretip üretmediğini kontrol et. Eğer cevap doğruysa kabul ver. Eğer cevap yanlışsa ve tüm kombinasyonlar denenmişse ret ver, eğer cevap yanlış ve tüm kombinasyonlar denenememişse 1’e dön.
Şimdi sıra NP’deki her dilin SAT diline polinom zamanda indirgemekte. A dilini nk zamanda kararlaştıran determinist olmayan bir N Turing Makinesi düşünelim. Aşağıda anlatacağım yöntem aracılığıyla N makinesini SAT diline indirgeyeceğiz.
Bu tabloda her bir satır N makinesinin konfigürasyonunu ifade ediyor. Kolaylık olsun diye her konfigürasyonun "#" ile başlayıp "#" ile bittiğini farz edelim. Her konfigürasyondan bir sonrakine N makinesinin geçiş fonksiyonu aracılığıyla ulaşılmaktadır yani konfigürasyonlar arasındaki geçişlerde N makinesinin kurallarına uyulmak zorundadır. Tüm satırlar bu kurallara uygun olarak doldurulduktan sonra tablo N makinesi için herhangi bir kabul durumu içeriyorsa A tablosu kabul verir yoksa ret verir. Böylelikle A dili bu tablo aracılığıyla simüle edilebilir. Böylelikle N makinesinin w’yı kabul etmesi artık tablonun qkabul durumunu içerip içermemesine indirgenmiş oldu. Şimdi sıra elde ettiğimiz tablodan SAT problemine geçmek için bir boolean formül (∅) elde etmeye geldi. F formülüne geçmeden önce kullanacağımız birkaç önemli terimi ifade edelim:
Q: N makinesinin durumları kümesi
Γ: N makinesinin alfabesi
C = Q ∪ Γ ∪ {#}: Tablodaki değişkenler kümesi
xi,j,s: ∅ formülünün değişkeni olup tablonun [i,j] gözünde s değeri varsa doğru yoksa yanlış değerini alır.
Şimdi F ifadesinin ne gibi koşulları sağlaması gerektiğine bakalım.
- Tablonun her hücresinde tek bir boolean değişken olmalıdır. Bunu göstermek için şu iki şart sağlanmalıdır.
- a. Tablonun her hücresinde en az bir değişken olmalıdır.
- b. Tablonun her hücresinde en fazla bir adet değişken olmalıdır.
- 2. Tablonun başlangıç konfigürasyonu N makinesinin başlangıç konfigürasyonu olmalıdır.
![image]()
doğrulanmalıdır.
- 3. Tabloda en az bir tane N makinesine ait kabul durumu (qkabul ) bulunmalıdır.
- Dolayısıyla
![image]()
doğrulanmalıdır.
- Dolayısıyla
- 4. Tablodaki konfigürasyonlar arasındaki geçiş N makinesinin kurallarına uygun olmalıdır.
![image]()
doğrulanmalıdır.
- Bir pencerenin geçerli olması ne demek onu inceleyelim. Tablonun 3×2’lik parçasına pencere diyoruz ve bu pencere geçiş fonksiyonuna uygunsa buna geçerli pencere diyoruz.
![{\displaystyle \mathrm {\text{Dolayısıyla }} \emptyset _{\mathrm {\text{hücre}} }=\bigwedge _{1\leq i,\ j\leq n^{k}}\left[\left(\bigvee _{s\in C}x_{i,j,s}\right)\scriptstyle \land \left(\bigwedge _{s,t\in C \atop s\neq t}\left({\overline {x_{i,j,s}}}\scriptstyle \lor {\overline {x_{i,j,t}}}\right)\right)\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4MVltTmhZMkZoWmpJM016VTFOVGt3TUdFMk16QmpPRGc1T0RsbFltSmtNRFZqTmpReVpqZzIuc3Zn.svg)
Dolayısıyla problemimiz ∅ = ∅hücre ∧ ∅ başlangıç ∧ ∅ kabul ∧ ∅ hareket probleminin doğrulanmasına indirgendi. Diğer bir deyişle A dilini SAT diline indirgemiş olduk.
İndirgemeyi yaptık şimdi bunun polinom zamanda olduğunu ispatlamaya geldi sıra. İndirgemenin karmaşıklığını göstermek için ∅ formülünün boyutu göstermek yeterli olacaktır. Tablonun boyutu nk ×nk olup n2k hücreye sahiptir ve bu hücrelerde l farklı değişken bulunabilir. (l∈C ). l değeri N makinesine verilen w katarından bağımsız olduğu için ∅ formülündeki değişken sayısı O(n2k) olacaktır. Dolayısıyla bu indirimin polinom zamanda yapılmış olduğu anlamına geliyor. Böylelikle SAT probleminin NP-tam olduğunu göstermiş olduk.
Sonuç
Şimdi bunun bize ne katacağını ifade edelim:
Farz edelim ki SAT problemine polinom zaman da bir çözüm bulunmuş olsun ("SAT ∈ P"). Bu bize şunu ifade eder SAT problemi hem NP sınıfının içinde (Cook-Levin teoreminden) hem de P sınıfının (varsayımdan) içinde ve diğer yandan her NP dili SAT problemine polinom zamanda indirgenebiliyor (Cook-Levin teoreminden) dolayısıyla bu NP sınıfı ile P sınıfın denk olduğu anlamına geliyor. Aslında Cook-Levin ikilisinin bu teorem ile amaçladıkları şey de tam olarak buydu yani P ile NP sınıfının eşitliğini iddia eden biri NP-tam sınıfından bir probleme polinom zamanda çözüm bulması iddiasını kanıtlamak için yeterli olacaktır.
Kaynakça
- ^ Michael Sipser: "Introduction to the Theory of Computation" Course Technology Press Second Edition, 2005.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
SAT problemi bir NP tam sinifi problemidir GirisTeoremin ispatina gecmeden once teoremin cikis noktasi uzerinde duralim Polinom zamanda kararlastirilan problem problemleri ile polinom zamanda dogrulanabilen problem problemleri siniflarinin birbirine denk olup olmadigi guncel matematik ve teorik bilgisayar biliminin bir turlu cozemedigi bir sorun olagelmistir Eger bu siniflar birbirine denk oldugu gosterilirse herhangi polinom zamanda dogrulanabilen bir problemin NP sinifi problemi artik polinom zamanda kararlastirilabiliyor olacagi kesin olarak soylenmis olacaktir 1970 lerde P ve NP siniflarinin arasindaki iliskiye Stephen Cook ve adindaki iki bilim adami farkli bir acidan yaklasmislardir bazi NP sinifi problemlerinin karmasikliklarinin tek baslarina tum NP sinifinin karmasikligina esit oldugunu fark etmisler Eger bu tip problemlerin polinom zamanda bir cozumu bulunursa NP sinifindaki tum problemler polinom zamanda cozulebilir Bu tip problemlere ileride deginecegiz ve bun tip problemlere NP tam sinifi problemleri diyecegiz Dolayisiyla Cook Levin yaklasiminin bir sonucu olarak P sinifiyla NP sinifinin esitligini iddia eden biri NP tam bir problemi polinom zamanda cozmesi iddiasini ispatlamak icin yeterli olacaktir SAT ProblemiSAT Dogrulanabilirlik probleminin ne oldugundan bahsedelim SAT problemi verilen bir boolean ifadenin sonucunun dogru olup olmayacagiyla problemidir Yani boolean ifadeyi dogru kilacak boolean ifadenin degiskenlerinin bir dogru yanlis kombinasyonunun olusturup olusturmayacagiyla ilgilenir Dolayisiyla SAT problemi asagidaki gibi ifade edilebilir SAT dogrulanabilir boolean ifadedir displaystyle SAT left langle varnothing rangle vert varnothing text dogrulanabilir boolean ifadedir right Ornegin x y x z displaystyle varnothing left bar x scriptstyle land y right scriptstyle lor left x scriptstyle land z right gibi herhangi bir boolean ifadenin sonucunun dogru olmasini inceleyen probleme SAT problemi denir Bu ornekte x dogru y yanlis z dogru icin problem dogrulanabilirdir NP Tam SinifiBir B dili NP tam ise su iki sarti saglamalidir B dili NP sinifindadir NP sinifindaki her dil B diline polinom zamanda indirgenebilir Burada yeni bir kavramla karsilasiyoruz Bunu fazla derine inmeden soyle ozetleyebiliriz eger bir problemin cozumunu bilmiyorsak ya da cozumu bulmakta cok zorlaniyorsak asil problemimizi cozmeye yardimci olacak yeni bir probleme indirgeriz ve cozume yeni indirgenmis problem araciligiyla ulasiriz Eger bu indirgememiz polinom zamanda gerceklestirilirse buna da polinom zamanda indirgemek adini veririz Buna soyle bir ornek verebiliriz Bilmediginiz bir yere gitmek istediginizi farz edelim ve bu problemin sizin icin zor bir problem oldugunu dusunelim Bu durumda gideceginiz yere ulasmak icin bir yardimciya ihtiyaciniz olacaktir Bu yardimcilar taksiye binmek harita elde etmek ya da bilen birine sormak bunlar arasinda sayilabilir Boylelikle bizim icin zor olan problemimiz taksi ya da harita bulmak kadar basit bir probleme indirgenmis oldu Kisaca buna da degindikten sonra artik teoremimize donelim IspatSAT probleminin NP tam sinifina ait bir problem oldugunu gostermek icin oncelikle SAT dilinin NP sinifinda oldugunu gostermemiz lazim SAT probleminin NP sinifinda oldugunu gostermenin iki farkli yolu vardir SAT problemini polinom zamanda dogrulayan bir Turing Makinesi TM tasarlamaliyiz Ya da SAT problemini polinom zamanda kararlastiran bir deterministik olmayan Turing Makinesi NTM tasarlamaliyiz Biz burada 2 yolla bunu ispatlayalim Deterministik olmayan N Turing Makinesi SAT dilini polinom zamanda asagidaki gibi kararlastirsin N nin Boolean ifade x1 x2 x3 xk nin de bu ifadenin bir degiskeni olsun ve makine girdi olarak lt x1 x2 x3 xk gt katarini alsin Deterministik olmayacak sekilde boolean ifadedeki degiskenlere dogru ve yanlis degerlerini ata Elde edilen kombinasyonla boolean formulun dogru cevap uretip uretmedigini kontrol et Eger cevap dogruysa kabul ver Eger cevap yanlissa ve tum kombinasyonlar denenmisse ret ver eger cevap yanlis ve tum kombinasyonlar denenememisse 1 e don Simdi sira NP deki her dilin SAT diline polinom zamanda indirgemekte A dilini nk zamanda kararlastiran determinist olmayan bir N Turing Makinesi dusunelim Asagida anlatacagim yontem araciligiyla N makinesini SAT diline indirgeyecegiz 453 337px Bu tabloda her bir satir N makinesinin konfigurasyonunu ifade ediyor Kolaylik olsun diye her konfigurasyonun ile baslayip ile bittigini farz edelim Her konfigurasyondan bir sonrakine N makinesinin gecis fonksiyonu araciligiyla ulasilmaktadir yani konfigurasyonlar arasindaki gecislerde N makinesinin kurallarina uyulmak zorundadir Tum satirlar bu kurallara uygun olarak doldurulduktan sonra tablo N makinesi icin herhangi bir kabul durumu iceriyorsa A tablosu kabul verir yoksa ret verir Boylelikle A dili bu tablo araciligiyla simule edilebilir Boylelikle N makinesinin w yi kabul etmesi artik tablonun qkabul durumunu icerip icermemesine indirgenmis oldu Simdi sira elde ettigimiz tablodan SAT problemine gecmek icin bir boolean formul elde etmeye geldi F formulune gecmeden once kullanacagimiz birkac onemli terimi ifade edelim Q N makinesinin durumlari kumesi G N makinesinin alfabesi C Q G Tablodaki degiskenler kumesi xi j s formulunun degiskeni olup tablonun i j gozunde s degeri varsa dogru yoksa yanlis degerini alir s Cxi j s xi j s1 xi j s2 xi j slC s1 s2 sl displaystyle begin array l bigvee s in C x i j s x i j s 1 scriptstyle land x i j s 2 scriptstyle land ldots scriptstyle land x i j s l C s 1 s 2 ldots s l end array Simdi F ifadesinin ne gibi kosullari saglamasi gerektigine bakalim Tablonun her hucresinde tek bir boolean degisken olmalidir Bunu gostermek icin su iki sart saglanmalidir a Tablonun her hucresinde en az bir degisken olmalidir b Tablonun her hucresinde en fazla bir adet degisken olmalidir Dolayisiyla hucre 1 i j nk s Cxi j s s t Cs t xi j s xi j t displaystyle mathrm text Dolayisiyla emptyset mathrm text hucre bigwedge 1 leq i j leq n k left left bigvee s in C x i j s right scriptstyle land left bigwedge s t in C atop s neq t left overline x i j s scriptstyle lor overline x i j t right right right dd dd 2 Tablonun baslangic konfigurasyonu N makinesinin baslangic konfigurasyonu olmalidir baslangic x1 1 x1 2 q0 x1 3 w1 x1 4 w2 x1 nk displaystyle emptyset mathrm text baslangic x 1 1 scriptstyle land x 1 2 q 0 scriptstyle land x 1 3 w 1 scriptstyle land x 1 4 w 2 dots scriptstyle land x 1 n k dogrulanmalidir dd dd 3 Tabloda en az bir tane N makinesine ait kabul durumu qkabul bulunmalidir Dolayisiyla kabul 1 i j nkxi j qkabul displaystyle emptyset mathrm kabul bigvee 1 leq i j leq n k chi i j q mathrm kabul dogrulanmalidir dd 4 Tablodaki konfigurasyonlar arasindaki gecis N makinesinin kurallarina uygun olmalidir hareket 1 lt i nk 1 lt j lt nk i j penceresi gecerli penceredir displaystyle emptyset mathrm hareket bigwedge 1 lt i leq n k 1 lt j lt n k left i j mathrm text penceresi gecerli penceredir right dogrulanmalidir dd Bir pencerenin gecerli olmasi ne demek onu inceleyelim Tablonun 3 2 lik parcasina pencere diyoruz ve bu pencere gecis fonksiyonuna uygunsa buna gecerli pencere diyoruz dd Dolayisiyla problemimiz hucre baslangic kabul hareket probleminin dogrulanmasina indirgendi Diger bir deyisle A dilini SAT diline indirgemis olduk Indirgemeyi yaptik simdi bunun polinom zamanda oldugunu ispatlamaya geldi sira Indirgemenin karmasikligini gostermek icin formulunun boyutu gostermek yeterli olacaktir Tablonun boyutu nk nk olup n2k hucreye sahiptir ve bu hucrelerde l farkli degisken bulunabilir l C l degeri N makinesine verilen w katarindan bagimsiz oldugu icin formulundeki degisken sayisi O n2k olacaktir Dolayisiyla bu indirimin polinom zamanda yapilmis oldugu anlamina geliyor Boylelikle SAT probleminin NP tam oldugunu gostermis olduk SonucSimdi bunun bize ne katacagini ifade edelim Farz edelim ki SAT problemine polinom zaman da bir cozum bulunmus olsun SAT P Bu bize sunu ifade eder SAT problemi hem NP sinifinin icinde Cook Levin teoreminden hem de P sinifinin varsayimdan icinde ve diger yandan her NP dili SAT problemine polinom zamanda indirgenebiliyor Cook Levin teoreminden dolayisiyla bu NP sinifi ile P sinifin denk oldugu anlamina geliyor Aslinda Cook Levin ikilisinin bu teorem ile amacladiklari sey de tam olarak buydu yani P ile NP sinifinin esitligini iddia eden biri NP tam sinifindan bir probleme polinom zamanda cozum bulmasi iddiasini kanitlamak icin yeterli olacaktir Kaynakca Michael Sipser Introduction to the Theory of Computation Course Technology Press Second Edition 2005