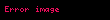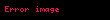Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Matematiğin bir dalı olan karmaşık analizde, korunmalı tekillik (diğer isimleri izole edilmiş tekillik veya korumalı tekilliktir) kendisine yakın başka bir tekilliğin olmadığı tekillik çeşididir.
Formel olarak, bir z karmaşık sayısı, f 'nin D - {z} kümesi (z 'nin D 'den kaldırıldığı küme) üzerinde holomorf olduğu z merkezli açık bir D diski varsa, f 'nin korunmalı tekilliğidir.
Bir meromorf fonksiyonun her tekilliği korunmalıdır ancak tekilliklerin korunması bir fonksiyonun meromorf olması için tek başına yeterli değildir. Laurent serisi ve kalıntı teoremi gibi karmaşık analizin çoğu aracı bütün ilişkin tekilliklerin korunmalı olmasını gerektirir.
Örnekler
![image]()
'nin 0'da korunmalı tekilliği vardır.- Kosekant fonksiyonu csc(πz), her tam sayıyı korunmalı tekillik olarak alır.
![image]()
fonksiyonunun 0'da korunmalı olmayan bir tekilliği vardır çünkü 0'a keyfi bir şekilde yakın olarak konuşlanmış her tam sayının (çarpmaya göre) tersinde, fonksiyonun ilave tekillikleri vardır.
Dış bağlantılar
- MathWorld14 Ağustos 2014 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir dali olan karmasik analizde korunmali tekillik diger isimleri izole edilmis tekillik veya korumali tekilliktir kendisine yakin baska bir tekilligin olmadigi tekillik cesididir Formel olarak bir z karmasik sayisi f nin D z kumesi z nin D den kaldirildigi kume uzerinde holomorf oldugu z merkezli acik bir D diski varsa f nin korunmali tekilligidir Bir meromorf fonksiyonun her tekilligi korunmalidir ancak tekilliklerin korunmasi bir fonksiyonun meromorf olmasi icin tek basina yeterli degildir Laurent serisi ve kalinti teoremi gibi karmasik analizin cogu araci butun iliskin tekilliklerin korunmali olmasini gerektirir Ornekler1z displaystyle frac 1 z nin 0 da korunmali tekilligi vardir Kosekant fonksiyonu csc pz her tam sayiyi korunmali tekillik olarak alir csc 1pz displaystyle csc left frac 1 pi z right fonksiyonunun 0 da korunmali olmayan bir tekilligi vardir cunku 0 a keyfi bir sekilde yakin olarak konuslanmis her tam sayinin carpmaya gore tersinde fonksiyonun ilave tekillikleri vardir Dis baglantilarMathWorld14 Agustos 2014 tarihinde Wayback Machine sitesinde