Çarpıklık (İngilizce: skewness; Fransızca: asymétrie) olasılık kuramı ve istatistik bilim dallarında bir reel-değerli rassal değişkenin olasılık dağılımının simetrik olamayışının ölçülmesidir.

Giriş
Grafikte gösterilen dağılım incelensin. Dağılımın sağ tarafında bulunan çubukların küçülmelerinin şekli sol taraftaki çubukların küçülmelerinden farklı bir görünüm vermektedir. Çubuk yüksekliklerinin küçüldükleri taraflara kuyruk adı verilir. Genel olarak iki çeşit olan çarpıklığın bilinmektedir.
Grafikteki kuyrukların görüntüsü dağılım için hangi tip çarpıklık olduğunu gösterir. Bu iki türlü çarpıklık ve bunu açıklayan grafiğin kuyruk konumu şunlardır:
- Pozitif çarpıklık: Bu halde sağdaki kuyruk daha uzundur. Dağılımın kütlesi grafiğin sol tarafında konsantre olmuştur. Bu türlü dağılım sağdan çarpık olarak anılır.
- Negatif çarpıklık: Bu halde soldaki kuyruk daha uzundur ve dağılımın kütlesi grafiğin sağ tarafında konsantre olmuştur. Bu türlü dağılım soldan çarpık olarak anılır.

Tanımlama
Çarpıklık üçüncü standardize edilmiş moment olup bu matematik notasyonla
olarak ifade edilmekte ve şöyle tanımlanmaktadır
Burada 



Bu tanımlama, basıklık tanımlanmasına bir analog benzetmedir; çünkü basıklık dördüncü kümülant ile ikinci kümülantın kare kökünün dördüncü üssü ifadesine bölümü arasındaki orantı ile ifade edilmektedir.
n sayıda gözlemi bulunan bir örneklem için örneklem çarpıklığı şöyle tanımlanır:
burada 
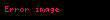

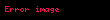
Eğer veriler örneklem içinse ve bilinen bir anakütleden gelmekte iseler, yukarıdaki formülleri kullanarak elde edilen örneklem çarpıklık ölçüleri için 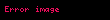
Burada 


Bir rassal değişken olan X için çarpıklık matematik kısaltma ile Çarp[X] olarak ifade edilsin. Eğer Y n tane bağımsız rassal değişkenlerin toplamından oluşuyorsa ve her bir X dağılımı birbiri ile ayni ise, Y nin çarpıklığı şöyle gösterilebilir
- Çarp[Y] = Çarp[X] / √n.
Çarpıklık özelliği birçok alanda pratik yarar sağlamaktadır. Pratik sorun çözümleri elde etmek için çok defa basitleştirilmiş model kullanılıp verilerin normal dağılım gösterdiği varsayılır. Bu varsayıma göre veriler ortalama etrafında simetrik olarak dağılmaktadırlar. Halbuki pratikte veriler çok defa kusursuzca simetrik değildirler. Böylece, verilerin çarpıklığını anlamak, kullanılan ortalamanın ne kadar simetriklikten uzak olabileceğini ve ne yönde veri merkezinin kullanılan ortalamadan değişik olacağını anlamaya yol açacaktır.
Pearson'un çarpıklık katsayıları
çarpıklık ölçülmesi için iki basit şekilde kestirim ölçüsü önermiştir. Bunlar
Ancak aynı veriler için, bu iki kestirim ölçüsünün aynı işarette olacağına ve eğrilerinin işaretinin grafikle görülebilen artı/eksi çarpıklık özelliğine benzeyeceğine hiçbir garanti bulunmamaktadır.
Yeni Bir Öneri
2014 yılında yayınlanan İstatistikte Altın Oran adlı bir kitapta, yeni bir çarpıklık katsayısı önerilmiştir.

Hesaplama; medyanın sol tarafındaki elemanların medyandan farklarının toplamının, medyanın sağ tarafındaki elemanların medyandan farklarının toplamına oranıdır. Eğer veri dizisinde, medyanın son tarafındaki elemanların medyandan farklarının toplamı (sol tarafın yükü), medyanın sağ tarafındaki elemanların medyandan farklarının toplamına (sağ tarafın yükü) eşitse, G = -1 olmaktadır. G = -1, tam simetri durumunu işaret eder. veri dizisinin medyana göre solu ile sağı, yük bakımından dengelidir. G, -1'den küçükse, medyanın sol tarafının yükü sağ tarafının yükünden fazladır dolayısıyla veri dizisi sola çarpıktır (veri dizisinin kuyruğu soldadır). G, -1'den büyükse, medyanın sağ tarafının yükü sol tarafının yükünden fazladır dolayısıyla veri dizisi sağa çarpıktır (veri dizisinin kuyruğu sağdadır). İstatistik literatüründe kullanılan diğer çarpıklık belirleme metodlarından farkı, veri dizisinin eleman sayısından bağımsız çalışabilmesi ve üstel (logaritmik vs) operatör içermediği için veri dizisinin formasyonundan bağımsız olmak üzere, çarpıklığı nicel olarak hesaplamaya olanak sağlamasıdır.
Ayrıca bakınız
Kaynakça
- ^
- ^ Gunver, Mehmet Guven; Senocak, Mustafa Sukru; Vehid, Suphi (2017) "To determine skewness, mean and deviation with new approach to contiuous data" PONTE International Journal of Sciences and Research Cilt:73/2 (Subat), " 2 Haziran 2018 tarihinde Wayback Machine sitesinde . doi:10.21506/j.ponte.2017.2.34
Dış kaynaklar
- Spiegel, Murray R ve Stephens, Larry J. (Tr.Çev.: Çelebioğlu, Salih) (2013) Istatistik, İstanbul: Nobel Akademik Yayıncılık
- Günver, Mehmet Güven; Șenocak, Mustafa Şükrü ve Vehid, Suphi (2014) İstatistikte Altın Oran, İstanbul:Türkmen Kitabevi, ISBN : 976054749409
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Carpiklik Ingilizce skewness Fransizca asymetrie olasilik kurami ve istatistik bilim dallarinda bir reel degerli rassal degiskenin olasilik dagiliminin simetrik olamayisinin olculmesidir Sifir olmayan carpiklik gosteren deneysel veri ornegiGirisGrafikte gosterilen dagilim incelensin Dagilimin sag tarafinda bulunan cubuklarin kuculmelerinin sekli sol taraftaki cubuklarin kuculmelerinden farkli bir gorunum vermektedir Cubuk yuksekliklerinin kuculdukleri taraflara kuyruk adi verilir Genel olarak iki cesit olan carpikligin bilinmektedir Grafikteki kuyruklarin goruntusu dagilim icin hangi tip carpiklik oldugunu gosterir Bu iki turlu carpiklik ve bunu aciklayan grafigin kuyruk konumu sunlardir Pozitif carpiklik Bu halde sagdaki kuyruk daha uzundur Dagilimin kutlesi grafigin sol tarafinda konsantre olmustur Bu turlu dagilim sagdan carpik olarak anilir Negatif carpiklik Bu halde soldaki kuyruk daha uzundur ve dagilimin kutlesi grafigin sag tarafinda konsantre olmustur Bu turlu dagilim soldan carpik olarak anilir TanimlamaCarpiklik ucuncu standardize edilmis moment olup bu matematik notasyonla g1 displaystyle gamma 1 olarak ifade edilmekte ve soyle tanimlanmaktadir g1 m3s3 displaystyle gamma 1 frac mu 3 sigma 3 Burada m3 displaystyle mu 3 ucuncu olarak ve s displaystyle sigma standart sapma olarak ifade edilmektedirler Ayni sekilde carpiklik ucuncu kumulant olan g1 displaystyle gamma 1 ile ikinci kumulantin yani k2 displaystyle kappa 2 nin kare kokunun ucuncu ussu olarak tanimlanmaktadir Bu tanimlama basiklik tanimlanmasina bir analog benzetmedir cunku basiklik dorduncu kumulant ile ikinci kumulantin kare kokunun dorduncu ussu ifadesine bolumu arasindaki oranti ile ifade edilmektedir n sayida gozlemi bulunan bir orneklem icin orneklem carpikligi soyle tanimlanir g1 m3m23 2 n i 1n xi x 3 i 1n xi x 2 3 2 displaystyle g 1 frac m 3 m 2 3 2 frac sqrt n sum i 1 n x i bar x 3 left sum i 1 n x i bar x 2 right 3 2 burada xi displaystyle x i ith orneklem degeri x displaystyle bar x m3 displaystyle m 3 orneklem ucuncu merkezsel momenti ve m2 displaystyle m 2 olur Eger veriler orneklem icinse ve bilinen bir anakutleden gelmekte iseler yukaridaki formulleri kullanarak elde edilen orneklem carpiklik olculeri icin g1 displaystyle g 1 bilinmeyen reel anakutle carpiklik olcusunun bir oldugu bilinmaktedir Bu nedenle bazi istatistikciler yanli olmayan carpiklik kestiricisi olarak su formulun kullanilmasini tavsiye ederler G1 k3k23 2 n n 1 n 2g1 displaystyle G 1 frac k 3 k 2 3 2 frac sqrt n n 1 n 2 g 1 Burada k3 displaystyle k 3 ucuncu kumulantin tek simetrik yanli olmayan kestricisi ve k2 displaystyle k 2 ikinci kumulantin simetrik yansiz kestiricisi olur Ne yaziktir ki buna ragmen G1 displaystyle G 1 de genel olarak yanli bir kestiricidir Bu kestiricinin beklenen degeri gercek anakutle carpiklik olcusunun ters isaretinde bile olabilmesi mumkundur Bir rassal degisken olan X icin carpiklik matematik kisaltma ile Carp X olarak ifade edilsin Eger Y n tane bagimsiz rassal degiskenlerin toplamindan olusuyorsa ve her bir X dagilimi birbiri ile ayni ise Y nin carpikligi soyle gosterilebilir Carp Y Carp X n Carpiklik ozelligi bircok alanda pratik yarar saglamaktadir Pratik sorun cozumleri elde etmek icin cok defa basitlestirilmis model kullanilip verilerin normal dagilim gosterdigi varsayilir Bu varsayima gore veriler ortalama etrafinda simetrik olarak dagilmaktadirlar Halbuki pratikte veriler cok defa kusursuzca simetrik degildirler Boylece verilerin carpikligini anlamak kullanilan ortalamanin ne kadar simetriklikten uzak olabilecegini ve ne yonde veri merkezinin kullanilan ortalamadan degisik olacagini anlamaya yol acacaktir Pearson un carpiklik katsayilaricarpiklik olculmesi icin iki basit sekilde kestirim olcusu onermistir Bunlar 3 ortalama 3 ortalama medyan Ancak ayni veriler icin bu iki kestirim olcusunun ayni isarette olacagina ve egrilerinin isaretinin grafikle gorulebilen arti eksi carpiklik ozelligine benzeyecegine hicbir garanti bulunmamaktadir Yeni Bir Oneri2014 yilinda yayinlanan Istatistikte Altin Oran adli bir kitapta yeni bir carpiklik katsayisi onerilmistir Coefficient of Skewness G Hesaplama medyanin sol tarafindaki elemanlarin medyandan farklarinin toplaminin medyanin sag tarafindaki elemanlarin medyandan farklarinin toplamina oranidir Eger veri dizisinde medyanin son tarafindaki elemanlarin medyandan farklarinin toplami sol tarafin yuku medyanin sag tarafindaki elemanlarin medyandan farklarinin toplamina sag tarafin yuku esitse G 1 olmaktadir G 1 tam simetri durumunu isaret eder veri dizisinin medyana gore solu ile sagi yuk bakimindan dengelidir G 1 den kucukse medyanin sol tarafinin yuku sag tarafinin yukunden fazladir dolayisiyla veri dizisi sola carpiktir veri dizisinin kuyrugu soldadir G 1 den buyukse medyanin sag tarafinin yuku sol tarafinin yukunden fazladir dolayisiyla veri dizisi saga carpiktir veri dizisinin kuyrugu sagdadir Istatistik literaturunde kullanilan diger carpiklik belirleme metodlarindan farki veri dizisinin eleman sayisindan bagimsiz calisabilmesi ve ustel logaritmik vs operator icermedigi icin veri dizisinin formasyonundan bagimsiz olmak uzere carpikligi nicel olarak hesaplamaya olanak saglamasidir Ayrica bakinizBasiklikKaynakca Gunver Mehmet Guven Senocak Mustafa Sukru Vehid Suphi 2017 To determine skewness mean and deviation with new approach to contiuous data PONTE International Journal of Sciences and Research Cilt 73 2 Subat 2 Haziran 2018 tarihinde Wayback Machine sitesinde doi 10 21506 j ponte 2017 2 34Dis kaynaklarSpiegel Murray R ve Stephens Larry J Tr Cev Celebioglu Salih 2013 Istatistik Istanbul Nobel Akademik Yayincilik ISBN 9786051337043 Gunver Mehmet Guven Șenocak Mustafa Sukru ve Vehid Suphi 2014 Istatistikte Altin Oran Istanbul Turkmen Kitabevi ISBN 976054749409
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State


