Olasılık kuramı ve bir dereceye kadar istatistik bilim dallarında basıklık (İngilizce: kurtosis) kavramı 1905da K. Pearson tarafından ilk defa açıklanmıştır. Basıklık kavramı bir değerli rassal değişken için olasılık dağılımının, grafik gösteriminden tanımlanarak ortaya çıkarılan bir kavram olan, sivriliği veya basıklığı özelliğinin ölçümüdür. Basıklık kavramının ayrıntıları olasılık kuramı içinde geliştirilmiştir. Betimsel istatistik için bir veri setinin basıklık karakteri pek dikkate alınmayan bir özellik olarak görülmektedir. Buna bir neden parametrik çıkarımsal istatistik alanında basıklık hakkında hemen hemen hiçbir kestirim veya sınama bulunmamasındandır ve pratik istatistik kullanımda basıklık pek önemsiz bir karakter olarak görülmektedir. Belki de basıklık ölçüsünün elle hesaplanmasının hemen hemen imkânsızlığı buna bir neden olmuştur.
Basıklık tanımlaması
Dördüncü şöyle tanımlanır;
Burada μ4 dördüncü ve σ standart sapmadır. Biraz eski istatistik kitaplarında bazen bu ifade basıklık tanımlaması olarak kullanılmaktaydı.
Daha alışılagelmiş bir şekilde basıklık, bir olasılık dağılımının "dördüncü kümülant değeri bölü varyans karesi" olarak şöyle tanımlanır:
Bu bir ölçü olarak kullanılırsa basıklık fazlalığı olarak bilinir. Formülün son terimi olan eksi 3 çok kere basıklık tanımlama formülüne yapılan bir ayarlama olarak açıklanır. Bu ayarlama sayesinde, normal eğrisinin basıklık ölçüsü değeri sıfır olur.
Bu ayarlamanın yapılmasının diğer bir nedeni ise birkaç rassal değişken toplamı için basıklık ölçüsünü incelemekle açıklanır. Ölçü kümülant kullanılarak tanımlandığı için eğer Y rassal değişkeni n tane istatistiksel bağımsız ve her biri aynı dağılım gösteren Xlerin bir toplamı ise; o halde
- Basıklık[Y] = Basıklık[X] / n,
olacaktır ve bu basit bir ortalama gibi görünüş verir. Bir genel ifade ile X1, ..., Xn rassal değişkenin hepsi aynı varyansa sahipler ve ayni dağılım gösterirlerse, toplam rassal değişken Y için basıklık şu olur:
Eğer ayar yapılmasa ve hatta dördüncü moment ölçü formülü olarak kullanılırsa idi bu basit toplam formülü ele geçmezdi.
Dördüncü standardize edilmiş moment için en küçük değer 1dir; bu nedenle en küçük basıklık fazlalığı değeri -2 olur. Dördüncü moment ve kümülant değeri için üst bir sınırlama yoktur ve üst değer artı sonsuz kadar büyük olabilir. Bu nedenle basıklık ölçüsü değeri -2 ile artı sonsuzluk arasında bulunabilir.
Terminoloji ve örneğinler
Eğer bir olasılık dağılımının veya veri setinin basıklık ölçüsü 0 (sıfır) değerde ise, bu çeşit veri seti veya olasılık dağılımına meso-basık (İngilizcesi 'meso-kurtic') adı verilir. Sıfır (0) basıklık ölçülü, yani meso-basık, en iyi bilinen olasılık dağılımı (parametreleri ne değerlerde olursa olsun) normal dağılımdır. Parametre değerlerine göre birkaç diğer olasılık dağılımı da meso-basık, yani 0 basıkliık ölçü değeri gösterirler. Örneğin, eğer 
'Basıklık' ölçüsü ve terminolojisi dağılım meso-basıklık karakteri göstermiyorsa bazen fikir karmaşıklığına yol açabilir.
Bir olasılık dağılımı veya bir veri seti için basıklık ölçüsü sıfırın üstünde pozitif (0 ile sonsuz arasında) olursa, bu türlü dağılıma lepto-basık adı verilir. Eğer bir olasılık dağılımı veya veri seti lepto-basık karakterli (yani pozitif basıklık ölçülü) ise, olasılık dağılım yoğunluk grafiği veya veri seti çokluluk grafiği, ortalama değerinde (normal dağılıma nazaran) daha sivri ve kuyrukları daha "şişman" olma görüntüsü verirler. Bu tip olasılık dağılımlarına şişman kuyruklu dağılım ve bazen de yüksek-Gauss tipi dağılım adı verilir. Laplace dağılımı ve logistik dağılım lepto-basık dağılımlara örnektirler. Basitçe bir ifade ile bir dağılımın ortası sivri, kuyrukları şişman ise, lepto-basık olur ve pozitif basıklık ölçüsü gösterir.
Bir olasılık dağlımı veya bir veri seti için basıklık ölçüsü sıfırın altında, negatif 0 ile -2 arasında olursa, bu türlü dağılıma plati-basık adı verilebilir. En alt sınırda basıklık ölçüsü -2 olan bir olasılık dağılım örneği, parametre değeri p = ½ olan bir Bernoulli dağılımıdır. Bu çeşit negatif basıklık ölçüsü gösteren dağılımların grafikleri ortalama etrafında düşük ve yayvan ve kuyrukları kısa sıska görünümünde veya ortası basık yamaçları dik yokuş bir "masa dağı" görünüşünde olurlar. Ayrık veya sürekli tekdüze dağılım ve dağılımı plati-basıklık (yani negatik basıklık ölçüsü) gösteren dağılımlara örnektirler. Bu türlü dağılımlar bir normal dağılımın yoğunluk grafiğine nazaran hem ortasında ve hem de kuyruklarında daha alçak görünüşlü olduğu için, alçak-Gauss tipi adı da verilir.
Eğer yukarıda verilen 'basıklık' ölçüsü yüksek pozitif değer gösteriyorsa dağılımın yoğunluk grafiğinde sivri bir doruk ve şişman kuyrukları bulunur; diğer taraftan basıklık ölçüsü negatif ve düşük ise (yani -2ye yakın), doruk daha yuvarlanmıştır ve genişçe yüksek omuzları bulunan bir "masa dağ" görünüşü almaktadır.
Grafik örneğinler
Pearson VII. tip ailesi

Basıklık özelliğinin etkileri bir parametrik dağılımlar ailesi olan ile gösterilebilir. Bu parametrik ailenin basıklık özelliği (düşük derecede momentler ve sabit kalırken) değiştirilebilmektedir. Bunlar için olasılık yoğunluk fonksiyonu şöyle verilmiştir:
Burada a bir ve m bir olurlar.
Bu aile için bütün olasılık yoğunluk fonksiyonları simetriktir. Eğer 




Limitte 
Bu gösterimde kırmızı eğridir.
Diğer tarafa yakınsalama, yani 
Mavi eğri basıklığı 2'ye eşit 
Bu aile içinde en üstteki eğri, meso-basık normal dağılıma kıyasla, çok lepto-basıklık karakteri gösterir. VII. tip Pearson yoğunluklarının doğasal üstel logaritmalarinin grafik gösterimi olan ikinci grafik ise lepto-basık yoğunlukların şişman kuyruklarını açıkça göstermektedir. Bu grafikte siyah renkli eğri ters bir parabolya benzeyen normal dağılım eğrisidir. Görülmektedir ki, basıklık derecesi 2 lepta-basık karakterli VII. tip Pearson dağılımın gösteren mavi eğri olan mavi eğriye nazaran, siyah normal eğri yoğunluk ortalamadan uzak bölgelere çok daha az olasılık vermektedir (yani "daha sıska kuyrukludur).
Bazı dağılımlar için basıklık


Bu gösterimlerde değişik parametrik ailelere bağlı olan bazı iyi bilinen dağılımlar karşılaştırılmaktadır. Tümünün yoğunluğu tek-modlu ve simetriktir. Her birinin ortalaması bulunmaktadır. Parametre değerleri öyle seçilmiştir ki bütün örneğinler için varyans bire eşittir. Doğrusal ölçekte ve logaritmalı ölçekte şu yedi dağılım karşılaştırılmaktadır:
- D: Laplace dağılımı - Bazen çift üstel dağılım denir. Kırmızı eğri (log-ölçekte grafikte iki doğru olarak görülmekte)- basıklık ölçümü = 3
- S: - turuncu eğri - basıklık ölçümü = 2
- L: logistik dağılım - yeşil eğri - basıklık ölçümü = 1.2
- N: normal dağılım - siyah eğri (log-ölçümünde tepesi aşağıda bir parabol) - basıklık ölçümü = 0
- C: -mavimsi eğri - basıklık ölçümü= −0.593762…
- W: - mavi eğri - basıklık ölçümü = -1
- U: sürekli tekdüze dağılım - morumsu eğri - basıklık ölçümü = -1.2
Örneklem için basıklık
n sayıda gözlem değeri bulunan bir için örneklem basıklığı şöyle ölçülür:
Burada m4 örneklem ortalaması etrafındaki örneklem dördüncü momenti, m2 ortalama etrafındaki ikinci moment (yahut , xi gözümlenen iinci değer ve 
Şu formül de
,
kullanılmaktadır, Burada n - örneklem büyüklüğü, D - hesaptan önce bilinen varyans değeri, xi x'inci ölçüm değeri ve 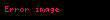
Anakütle basıklık kestirimcileri
Bir anakütleden bir altset olan örneklem verilirse, yukarıda verilmiş olan örneklem basıklık ölçüsü anakütle basıklık ölçüsünün olur. Bilgisayar için hazırlanmış istatistik paketleri (SAS, Minitab, SPSS ve Excel) anakütle basıklık kestirimci değeri G için şu formülü kullanmaktadır:|- | |




Sadece istatistik paketi bu formülü kullanmaktadır.
Ne yazıktır ki bu 
Ayrıca bakınız
Kaynakça
- ^ Karl Pearson (1905) in "Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson. A Rejoinder," Biometrika, Cilt 4, say. 169-212 (Almanca)
- ^ İngilizce "lepta-kurtic" ve lepto- antik Yunanca'dan alınma
- ^ "Sivri", yani basık olmayan, görünüşlü dağılımların pozitif basıklık ölçüsü gösterme karakteri olması, fikir karışıklığına yol açabilir. Belki kavramın adına sivrilik demek veya kavramın adına kurtosis deyip bir fikir karışıklığından kaçınmak daha doğru olabilecektir. Ama sonunda bunun öğrenilerek kabul edilmesi gerekir.
- ^ İngilizce "plati-kurtic" ve plati- antik Yunanca'dan alınma. Ayrıca basıklık ölçüsünün en küçük değerinin -2 olmasına dikkat edilmelidir.
- ^ Bu türlü tepesi geniş ve düz, basık bir "masa dağı" görünüşlü grafiği olan bir dağılımın basıklık ölçüsünün negatif olması bazen fikir karışıklığına yol açmaktadır. Bu nedenle bunun öğrenme için özellikle ele alınması uygundur.
Dış kaynaklar
- Spiegel, Murray R ve Stephens, Larry J. (Tr.Çev.: Çelebioğlu, Salih) (2013) İstatistik, İstanbul: Nobel Akademik Yayıncılık
Dış bağlantılar
- Bedava Online Yazılım (Hesaplayıcı): Herhangi veri grubu için değişik çarpıklık ve basıklık ölçülerini hesaplar. Küçük ve büyük örneklemler için sınamalar uygular) (İngilizce)
- Matematik bilimi içinde bazı kavram isimlerinin ilk defa kullanılmaları hakkında bir seri yazı17 Ocak 1999 tarihinde Wayback Machine sitesinde . (İngilizce)
- (İngilizce)
- Joanes, D. N. ve Gill, C. A. (1998) "Comparing measures of sample skewness and kurtosis" Journal of the (Series D): The Statistician Cilt:47/1 Sayfa:183-189. doi:10.1111/1467-9884.00122 (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami ve bir dereceye kadar istatistik bilim dallarinda basiklik Ingilizce kurtosis kavrami 1905da K Pearson tarafindan ilk defa aciklanmistir Basiklik kavrami bir degerli rassal degisken icin olasilik dagiliminin grafik gosteriminden tanimlanarak ortaya cikarilan bir kavram olan sivriligi veya basikligi ozelliginin olcumudur Basiklik kavraminin ayrintilari olasilik kurami icinde gelistirilmistir Betimsel istatistik icin bir veri setinin basiklik karakteri pek dikkate alinmayan bir ozellik olarak gorulmektedir Buna bir neden parametrik cikarimsal istatistik alaninda basiklik hakkinda hemen hemen hicbir kestirim veya sinama bulunmamasindandir ve pratik istatistik kullanimda basiklik pek onemsiz bir karakter olarak gorulmektedir Belki de basiklik olcusunun elle hesaplanmasinin hemen hemen imkansizligi buna bir neden olmustur Basiklik tanimlamasiDorduncu soyle tanimlanir m4s4 displaystyle frac mu 4 sigma 4 Burada m4 dorduncu ve s standart sapmadir Biraz eski istatistik kitaplarinda bazen bu ifade basiklik tanimlamasi olarak kullanilmaktaydi Daha alisilagelmis bir sekilde basiklik bir olasilik dagiliminin dorduncu kumulant degeri bolu varyans karesi olarak soyle tanimlanir g2 k4k22 m4s4 3 displaystyle gamma 2 frac kappa 4 kappa 2 2 frac mu 4 sigma 4 3 Bu bir olcu olarak kullanilirsa basiklik fazlaligi olarak bilinir Formulun son terimi olan eksi 3 cok kere basiklik tanimlama formulune yapilan bir ayarlama olarak aciklanir Bu ayarlama sayesinde normal egrisinin basiklik olcusu degeri sifir olur Bu ayarlamanin yapilmasinin diger bir nedeni ise birkac rassal degisken toplami icin basiklik olcusunu incelemekle aciklanir Olcu kumulant kullanilarak tanimlandigi icin eger Y rassal degiskeni n tane istatistiksel bagimsiz ve her biri ayni dagilim gosteren Xlerin bir toplami ise o halde Basiklik Y Basiklik X n olacaktir ve bu basit bir ortalama gibi gorunus verir Bir genel ifade ile X1 Xn rassal degiskenin hepsi ayni varyansa sahipler ve ayni dagilim gosterirlerse toplam rassal degisken Y icin basiklik su olur Basik i 1nXi 1n2 i 1nBasik Xi displaystyle operatorname Basik left sum i 1 n X i right 1 over n 2 sum i 1 n operatorname Basik X i Eger ayar yapilmasa ve hatta dorduncu moment olcu formulu olarak kullanilirsa idi bu basit toplam formulu ele gecmezdi Dorduncu standardize edilmis moment icin en kucuk deger 1dir bu nedenle en kucuk basiklik fazlaligi degeri 2 olur Dorduncu moment ve kumulant degeri icin ust bir sinirlama yoktur ve ust deger arti sonsuz kadar buyuk olabilir Bu nedenle basiklik olcusu degeri 2 ile arti sonsuzluk arasinda bulunabilir Terminoloji ve orneginlerEger bir olasilik dagiliminin veya veri setinin basiklik olcusu 0 sifir degerde ise bu cesit veri seti veya olasilik dagilimina meso basik Ingilizcesi meso kurtic adi verilir Sifir 0 basiklik olculu yani meso basik en iyi bilinen olasilik dagilimi parametreleri ne degerlerde olursa olsun normal dagilimdir Parametre degerlerine gore birkac diger olasilik dagilimi da meso basik yani 0 basikliik olcu degeri gosterirler Ornegin eger p 1 2 1 12 displaystyle p 1 2 pm sqrt 1 12 ise bir binom dagilim meso basiktir Basiklik olcusu ve terminolojisi dagilim meso basiklik karakteri gostermiyorsa bazen fikir karmasikligina yol acabilir Bir olasilik dagilimi veya bir veri seti icin basiklik olcusu sifirin ustunde pozitif 0 ile sonsuz arasinda olursa bu turlu dagilima lepto basik adi verilir Eger bir olasilik dagilimi veya veri seti lepto basik karakterli yani pozitif basiklik olculu ise olasilik dagilim yogunluk grafigi veya veri seti cokluluk grafigi ortalama degerinde normal dagilima nazaran daha sivri ve kuyruklari daha sisman olma goruntusu verirler Bu tip olasilik dagilimlarina sisman kuyruklu dagilim ve bazen de yuksek Gauss tipi dagilim adi verilir Laplace dagilimi ve logistik dagilim lepto basik dagilimlara ornektirler Basitce bir ifade ile bir dagilimin ortasi sivri kuyruklari sisman ise lepto basik olur ve pozitif basiklik olcusu gosterir Bir olasilik daglimi veya bir veri seti icin basiklik olcusu sifirin altinda negatif 0 ile 2 arasinda olursa bu turlu dagilima plati basik adi verilebilir En alt sinirda basiklik olcusu 2 olan bir olasilik dagilim ornegi parametre degeri p olan bir Bernoulli dagilimidir Bu cesit negatif basiklik olcusu gosteren dagilimlarin grafikleri ortalama etrafinda dusuk ve yayvan ve kuyruklari kisa siska gorunumunde veya ortasi basik yamaclari dik yokus bir masa dagi gorunusunde olurlar Ayrik veya surekli tekduze dagilim ve dagilimi plati basiklik yani negatik basiklik olcusu gosteren dagilimlara ornektirler Bu turlu dagilimlar bir normal dagilimin yogunluk grafigine nazaran hem ortasinda ve hem de kuyruklarinda daha alcak gorunuslu oldugu icin alcak Gauss tipi adi da verilir Eger yukarida verilen basiklik olcusu yuksek pozitif deger gosteriyorsa dagilimin yogunluk grafiginde sivri bir doruk ve sisman kuyruklari bulunur diger taraftan basiklik olcusu negatif ve dusuk ise yani 2ye yakin doruk daha yuvarlanmistir ve genisce yuksek omuzlari bulunan bir masa dag gorunusu almaktadir Grafik orneginlerPearson VII tip ailesi VII tip Pearson dagiliminda basiklik sonsuz kirmizi 2 mavi ve 0 siyah Basiklik ozelliginin etkileri bir parametrik dagilimlar ailesi olan ile gosterilebilir Bu parametrik ailenin basiklik ozelligi dusuk derecede momentler ve sabit kalirken degistirilebilmektedir Bunlar icin olasilik yogunluk fonksiyonu soyle verilmistir f x a m G m apG m 1 2 1 xa 2 m displaystyle f x a m frac Gamma m a sqrt pi Gamma m 1 2 left 1 left frac x a right 2 right m Burada a bir ve m bir olurlar Bu aile icin butun olasilik yogunluk fonksiyonlari simetriktir Eger m gt k 1 2 displaystyle m gt k 1 2 anlamli ise kinci moment de bulunur 0dan degisik bir basiklik olcusu bulunmasi icin m gt 5 2 displaystyle m gt 5 2 olmasi gerekmektedir O halde hem ortalama hem de carpiklik aynen sifira esit olurlar a degeri a2 2m 3 displaystyle a 2 2m 3 olacak sekilde secilirse varyans degeri 1e esit olur Bu kosullar altinda tek serbestce degistirilebilecek parametre m olur ve bu dorduncu moment ve kumulant yani basiklik ozelligini kontrol eder Bu dagilim fonksiyonu m 5 2 3 g2 displaystyle m 5 2 3 gamma 2 olarak parametrelenebilir ve burada g2 displaystyle gamma 2 basiklik olcusu olur Bunun sonucunda bir parametreli lepto basik aile elde edilir ve bunlar icin ortalamalar hep 0 varyanslar hep 1 carpiklik hep 0 ve basiklik yukarida verilmis sekilde degisken olur Bu halde olasilik yogunluk fonksiyonu soyle verilir g x g2 f x a 2 6 g2 m 5 2 3 g2 displaystyle g x gamma 2 f x a sqrt 2 6 gamma 2 m 5 2 3 gamma 2 Limitte g2 displaystyle gamma 2 to infty yakinsalamsi ile olasilik yogunluk fonksiyonu su sekli alir g x 3 2 x2 5 2 displaystyle g x 3 left 2 x 2 right 5 2 Bu gosterimde kirmizi egridir Diger tarafa yakinsalama yani g2 0 displaystyle gamma 2 to 0 limitte dagilim olarak verir ve bu siyah egri olarak gosterilmistir Mavi egri basikligi 2 ye esit x g x 2 displaystyle x mapsto g x 2 olasilik yogunluk gosterir Mavi egri ile siyah egri arasinda olasilik yogunluklari 2 1 1 2 1 4 1 8 ve 1 16 olarak elde edilen egriler verilir Kirmizi egri VII Tip Pearson dagilimlari icin g2 displaystyle gamma 2 infty ile yani dorduncu momenti bulunmayan bir yukari limit verir Bu kirmizi egri icin egri orijinden uzaklastikca en az dusus gosterir yani sisman kuyruklari vardir Bu aile icinde en ustteki egri meso basik normal dagilima kiyasla cok lepto basiklik karakteri gosterir VII tip Pearson yogunluklarinin dogasal ustel logaritmalarinin grafik gosterimi olan ikinci grafik ise lepto basik yogunluklarin sisman kuyruklarini acikca gostermektedir Bu grafikte siyah renkli egri ters bir parabolya benzeyen normal dagilim egrisidir Gorulmektedir ki basiklik derecesi 2 lepta basik karakterli VII tip Pearson dagilimin gosteren mavi egri olan mavi egriye nazaran siyah normal egri yogunluk ortalamadan uzak bolgelere cok daha az olasilik vermektedir yani daha siska kuyrukludur Bazi dagilimlar icin basiklik Bu gosterimlerde degisik parametrik ailelere bagli olan bazi iyi bilinen dagilimlar karsilastirilmaktadir Tumunun yogunlugu tek modlu ve simetriktir Her birinin ortalamasi bulunmaktadir Parametre degerleri oyle secilmistir ki butun orneginler icin varyans bire esittir Dogrusal olcekte ve logaritmali olcekte su yedi dagilim karsilastirilmaktadir D Laplace dagilimi Bazen cift ustel dagilim denir Kirmizi egri log olcekte grafikte iki dogru olarak gorulmekte basiklik olcumu 3 S turuncu egri basiklik olcumu 2 L logistik dagilim yesil egri basiklik olcumu 1 2 N normal dagilim siyah egri log olcumunde tepesi asagida bir parabol basiklik olcumu 0 C mavimsi egri basiklik olcumu 0 593762 W mavi egri basiklik olcumu 1 U surekli tekduze dagilim morumsu egri basiklik olcumu 1 2Orneklem icin basiklikn sayida gozlem degeri bulunan bir icin orneklem basikligi soyle olculur g2 m4m22 3 n i 1n xi x 4 i 1n xi x 2 2 3 displaystyle g 2 frac m 4 m 2 2 3 frac n sum i 1 n x i overline x 4 left sum i 1 n x i overline x 2 right 2 3 Burada m4 orneklem ortalamasi etrafindaki orneklem dorduncu momenti m2 ortalama etrafindaki ikinci moment yahut xi gozumlenen iinci deger ve x displaystyle overline x ise orneklem ortalamasidir Su formul de D 1n i 1n xi x 2 displaystyle D 1 over n sum i 1 n x i bar x 2 E 1nD2 i 1n xi x 4 3 displaystyle E 1 over nD 2 sum i 1 n x i bar x 4 3 kullanilmaktadir Burada n orneklem buyuklugu D hesaptan once bilinen varyans degeri xi x inci olcum degeri ve x displaystyle bar x hesaptan once bilinen ortalama degeri olurlar Anakutle basiklik kestirimcileriBir anakutleden bir altset olan orneklem verilirse yukarida verilmis olan orneklem basiklik olcusu anakutle basiklik olcusunun olur Bilgisayar icin hazirlanmis istatistik paketleri SAS Minitab SPSS ve Excel anakutle basiklik kestirimci degeri G icin su formulu kullanmaktadir n2 n 1 m4 3 n 1 m22 n 1 n 2 n 3 n 1 2n2m22 displaystyle frac n 2 n 1 m 4 3 n 1 m 2 2 n 1 n 2 n 3 frac n 1 2 n 2 m 2 2 n 1 n 2 n 3 n 1 m4m22 3 n 1 displaystyle frac n 1 n 2 n 3 left n 1 frac m 4 m 2 2 3 n 1 right n 1 n 2 n 3 n 1 g2 6 displaystyle frac n 1 n 2 n 3 left n 1 g 2 6 right n 1 n n 1 n 2 n 3 i 1n xi x 4 i 1n xi x 2 2 3 n 1 2 n 2 n 3 displaystyle frac n 1 n n 1 n 2 n 3 frac sum i 1 n x i bar x 4 left sum i 1 n x i bar x 2 right 2 3 frac n 1 2 n 2 n 3 n 1 n n 1 n 2 n 3 i 1n xi x 4k22 3 n 1 2 n 2 n 3 displaystyle frac n 1 n n 1 n 2 n 3 frac sum i 1 n x i bar x 4 k 2 2 3 frac n 1 2 n 2 n 3 Burada k4 dorduncu kumulant degerinin tek simetrik yanli olmayan kestirimidir k2 anakutle varyansi icin yanli olmayan kestirim degeridir m4 ortalama etrafinda dorduncu orneklem momentidir m2 orneklem varyansidir xiiinci deger ve x displaystyle bar x orneklem ortalamasidir Sadece istatistik paketi bu formulu kullanmaktadir Ne yaziktir ki bu G2 displaystyle G 2 kendisi genellikle yanli kestirimdir Bu sadece bir normal dagilim icin yanli degildir cunku o halde beklenen degeri sifir olmaktadir Ayrica bakinizCarpiklikKaynakca Karl Pearson 1905 in Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson A Rejoinder Biometrika Cilt 4 say 169 212 Almanca Ingilizce lepta kurtic ve lepto antik Yunanca dan alinma Sivri yani basik olmayan gorunuslu dagilimlarin pozitif basiklik olcusu gosterme karakteri olmasi fikir karisikligina yol acabilir Belki kavramin adina sivrilik demek veya kavramin adina kurtosis deyip bir fikir karisikligindan kacinmak daha dogru olabilecektir Ama sonunda bunun ogrenilerek kabul edilmesi gerekir Ingilizce plati kurtic ve plati antik Yunanca dan alinma Ayrica basiklik olcusunun en kucuk degerinin 2 olmasina dikkat edilmelidir Bu turlu tepesi genis ve duz basik bir masa dagi gorunuslu grafigi olan bir dagilimin basiklik olcusunun negatif olmasi bazen fikir karisikligina yol acmaktadir Bu nedenle bunun ogrenme icin ozellikle ele alinmasi uygundur Dis kaynaklarSpiegel Murray R ve Stephens Larry J Tr Cev Celebioglu Salih 2013 Istatistik Istanbul Nobel Akademik Yayincilik ISBN 9786051337043Dis baglantilarBedava Online Yazilim Hesaplayici Herhangi veri grubu icin degisik carpiklik ve basiklik olculerini hesaplar Kucuk ve buyuk orneklemler icin sinamalar uygular Ingilizce Matematik bilimi icinde bazi kavram isimlerinin ilk defa kullanilmalari hakkinda bir seri yazi17 Ocak 1999 tarihinde Wayback Machine sitesinde Ingilizce Ingilizce Joanes D N ve Gill C A 1998 Comparing measures of sample skewness and kurtosis Journal of the Series D The Statistician Cilt 47 1 Sayfa 183 189 doi 10 1111 1467 9884 00122 Ingilizce
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State








