Geometride, çevre açı, çember ĂŒzerinde iki sekant (kesen) çizgisi kesiĆtiÄinde bir çember ĂŒzerinde oluĆan açıdır. Ăember ĂŒzerindeki bir nokta (açının tepe noktası) ile çember ĂŒzerinde verilen diÄer iki noktanın oluĆturduÄu açı olarak da tanımlanabilir.

EĆdeÄer olarak, bir çevre açı, bir bitiĆ noktasını paylaĆan çemberin iki kiriĆiyle tanımlanır.
Ăevre açı teoremi, bir çevre açının ölĂ§ĂŒsĂŒnĂŒ, aynı yayı oluĆturan ölĂ§ĂŒsĂŒ ile iliĆkilendirir.
Ăevre açı teoremi, Ăklid'in "Elementler" kitabının 3. kitabında Ănerme 20 olarak görĂŒnĂŒr.
Teorem
Açıklama

 ve
ve  noktaları için,
noktaları için,  açısının eĆit olduÄu dĂŒzlemdeki
açısının eĆit olduÄu dĂŒzlemdeki  noktaları kĂŒmesiÂ
noktaları kĂŒmesi  bir çemberin yaydır.
bir çemberin yaydır.  'nun çemberin merkezi olduÄu
'nun çemberin merkezi olduÄu  'nin ölĂ§ĂŒsĂŒ,Â
'nin ölĂ§ĂŒsĂŒ,  'dır.
'dır.Ăevre açı teoremi, bir çember içine çizilmiĆ bir 

Ä°spat
Bir kiriĆin çap olduÄu çevre açılar

Ćekilde görĂŒldĂŒÄĂŒ gibi 






















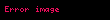


Bir ĂŒĂ§genin ĂŒĂ§ açısının toplamının 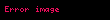

.
Bu nedenle,
Her iki taraftan 180° çıkarırsak,
burada 



Ăemberin merkezi, açının içinde kalan çevre açılar

Merkezi 










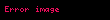
Bu yayın, içinde 




Bu nedenle,
o zaman,
Böylece
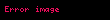




olsun, böylece
Birinci bölĂŒmden biliyoruz ki 

bu nedenle, denklem (1)'den aĆaÄıdaki sonuç elde edilir:
Ăemberin merkezi, açının dıĆında kalan çevre açılar

Ănceki durum, çevre açının ölĂ§ĂŒsĂŒnĂŒn, bu ispatın ilk bölĂŒmĂŒnde tartıĆıldıÄı gibi iki çevre açı arasındaki fark olduÄu durumu kapsayacak Ćekilde geniĆletilebilir.
Merkezi 










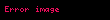
Bu yayın, içinde 




Bu nedenle,
.
o zaman,
olsun, böylece
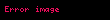




olsun, böylece
Birinci bölĂŒmden biliyoruz ki 

bu nedenle, denklem (3) ile aĆaÄıdaki ifadeye ulaĆılır:
Sonuç
Benzer bir argĂŒmana göre, bir kiriĆ ile onun kesiĆme noktalarından birinde teÄet doÄrusu arasındaki açı, kiriĆin kapsadıÄı merkezi açının yarısına eĆittir. Ayrıca bkz. .
Uygulamalar
Ăevre açı teoremi, dĂŒzlemin temel Ăklid geometrisinin birçok ispatında kullanılır. Teoremin özel bir durumu, bir çapın kapsadıÄı açının her zaman 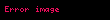
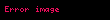
Elipsler, hiperboller ve paraboller için çevre açı teoremleri
Ăevre açı teoremleri elipsler, hiperboller ve paraboller için de mevcuttur. Temel farklar, bir açının ölĂ§ĂŒmleridir. (Bir açı, bir çift kesiĆen çizgi olarak kabul edilir.)
Kaynakça
- (1990). Excursions in Geometry. Dover. ss. 17-23. ISBN .
- Gellert W., KĂŒstner H., Hellwich M., KĂ€stner H. (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. s. 172. ISBN .
- Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2. bas.). Reading: Addison-Wesley. ss. 192-197. ISBN .
DÄ±Ć baÄlantılar
- Eric W. Weisstein, Inscribed Angle (MathWorld)
- . 11 Mayıs 2009 tarihinde kaynaÄından arĆivlendi.
- . cut-the-knot.org. 15 Nisan 2003 tarihinde kaynaÄından arĆivlendi.
- . 30 Ekim 2006 tarihinde kaynaÄından arĆivlendi.
(etkileĆimli animasyon ile)
- . 30 Ekim 2006 tarihinde kaynaÄından arĆivlendi.
(etkileĆimli animasyon ile)
- . 30 Ekim 2006 tarihinde kaynaÄından arĆivlendi.
(etkileĆimli animasyon ile)
- . bookofproofs.org. 11 Temmuz 2020 tarihinde kaynaÄından arĆivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kĂŒtĂŒphane, kĂŒtĂŒbhane, ara, ara bul, bul, herĆey, ne arasanız burada,hikayeler, makale, kitaplar, öÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tĂŒrk, tĂŒrkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ĂŒcretsiz, ĂŒcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mĂŒzik, Ćarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Geometride cevre aci cember uzerinde iki sekant kesen cizgisi kesistiginde bir cember uzerinde olusan acidir Cember uzerindeki bir nokta acinin tepe noktasi ile cember uzerinde verilen diger iki noktanin olusturdugu aci olarak da tanimlanabilir Cevre aci 8 displaystyle theta cember uzerindeki ayni yayi olusturan veya goren merkezi aci 28 displaystyle 2 theta nin yarisidir Boylece 8 displaystyle theta acisi tepe noktasi cember uzerinde hareket ettirildikce degismez Esdeger olarak bir cevre aci bir bitis noktasini paylasan cemberin iki kirisiyle tanimlanir Cevre aci teoremi bir cevre acinin olcusunu ayni yayi olusturan olcusu ile iliskilendirir Cevre aci teoremi Oklid in Elementler kitabinin 3 kitabinda Onerme 20 olarak gorunur TeoremAciklama Sabit A displaystyle A ve B displaystyle B noktalari icin AMB displaystyle angle AMB acisinin esit oldugu duzlemdeki M displaystyle M noktalari kumesi a displaystyle alpha bir cemberin yaydir O displaystyle O nun cemberin merkezi oldugu AOB displaystyle angle AOB nin olcusu 2a displaystyle 2 alpha dir Cevre aci teoremi bir cember icine cizilmis bir 8 displaystyle theta acisinin cember uzerindeki ayni yaya karsilik gelen veya ayni yayi goren merkezi aci 28 displaystyle 2 theta nin yarisi oldugunu belirtir Bu nedenle tepesi cember uzerinde farkli konumlara tasindiginda aci degismez Ispat Bir kirisin cap oldugu cevre acilar Durum Bir kiris captir Sekilde goruldugu gibi O displaystyle O bir cemberin merkezi olsun Cember uzerinde iki nokta secelim ve bunlara V displaystyle V ve A displaystyle A diyelim VO displaystyle VO dogrusunu cizelim ve O displaystyle O yu gececek sekilde uzatalim boylece V displaystyle V noktasinin capa gore zitti olan B displaystyle B noktasinda cemberle kesisir Tepe noktasi V displaystyle V olan ve kenarlari A displaystyle A ve B displaystyle B noktalarindan gecen bir aci cizelim OA displaystyle OA dogrusunu cizelim Aci BOA displaystyle BOA bir buna 8 displaystyle theta diyelim OV displaystyle OV ve OA displaystyle OA cizgilerinin her ikisi de cemberin yaricaplaridir bu nedenle esit uzunluklara sahiptirler Bu nedenle VOA displaystyle triangle VOA ucgeni ikizkenardir oyle ise BVA displaystyle angle BVA acisi cevre aci ve VAO displaystyle angle VAO acisi esittir her birini ps displaystyle psi olarak gosterelim BOA displaystyle angle BOA ve AOV displaystyle angle AOV acilari butunlerdir O displaystyle O dan gecen VB displaystyle VB cizgisi duz bir dogru olana kadar toplamlari 180 displaystyle 180 circ ye kadar artar Bu nedenle AOV displaystyle angle AOV acisinin olcusu olarak 180 8 displaystyle 180 circ theta alinabilir Bir ucgenin uc acisinin toplaminin 180 displaystyle 180 circ oldugu ve VOA displaystyle triangle VOA ucgeninin uc acisinin aci1 180 8 displaystyle text aci 1 180 circ theta aci2 ps displaystyle text aci 2 psi aci3 ps displaystyle text aci 3 psi Bu nedenle 2ps 180 8 180 displaystyle 2 psi 180 circ theta 180 circ Her iki taraftan 180 cikarirsak 2ps 8 displaystyle 2 psi theta burada 8 displaystyle theta AB displaystyle AB yayini goren merkez aci ve ps displaystyle psi AB displaystyle AB yayini olusturan cevre acidir Cemberin merkezi acinin icinde kalan cevre acilar Durum Icten aciya merkez Merkezi O displaystyle O noktasi olan bir cember verildiginde cember uzerinde uc nokta V displaystyle V C displaystyle C ve D displaystyle D alalim VC displaystyle VC ve VD displaystyle VD dogrularini cizelim DVC displaystyle angle DVC acisi bir cevre acidir Simdi VO displaystyle VO dogrusunu cizelim ve onu E displaystyle E noktasinda cemberle kesisecek sekilde O displaystyle O noktasini gececek sekilde uzatalim DVC displaystyle angle DVC acisi cember uzerindeki DC displaystyle DC yayini gorur Bu yayin icinde E displaystyle E noktasini icerdigini varsayalim E displaystyle E noktasi V displaystyle V noktasinin capa gore karsisidir DVE displaystyle angle DVE ve EVC displaystyle angle EVC acilari da cevre acilardir ancak bu acilarin her ikisi de cemberin merkezinden gecen bir kenara sahiptir bu nedenle yukaridaki Bolum 1 deki teorem bunlara uygulanabilir Bu nedenle DVC DVE EVC displaystyle angle DVC angle DVE angle EVC o zaman ps0 DVC displaystyle psi 0 angle DVC ps1 DVE displaystyle psi 1 angle DVE ps2 EVC displaystyle psi 2 angle EVC Boylece ps0 ps1 ps2 1 displaystyle psi 0 psi 1 psi 2 qquad qquad 1 OC displaystyle OC ve OD displaystyle OD dogrularini cizelim DOE displaystyle angle DOE ve EOC displaystyle angle EOC acilari gibi DOC displaystyle angle DOC acisi da merkezi bir acidir ve DOC DOE EOC displaystyle angle DOC angle DOE angle EOC 80 DOC displaystyle theta 0 angle DOC 81 DOE displaystyle theta 1 angle DOE 82 EOC displaystyle theta 2 angle EOC olsun boylece 80 81 82 2 displaystyle theta 0 theta 1 theta 2 qquad qquad 2 Birinci bolumden biliyoruz ki 81 2ps1 displaystyle theta 1 2 psi 1 ve 82 2ps2 displaystyle theta 2 2 psi 2 dir Bu sonuclarin denklem 2 ile birlestirilmesi asagidaki sonucu verir 80 2ps1 2ps2 2 ps1 ps2 displaystyle theta 0 2 psi 1 2 psi 2 2 psi 1 psi 2 bu nedenle denklem 1 den asagidaki sonuc elde edilir 80 2ps0 displaystyle theta 0 2 psi 0 Cemberin merkezi acinin disinda kalan cevre acilar Durum Merkez acinin disinda Onceki durum cevre acinin olcusunun bu ispatin ilk bolumunde tartisildigi gibi iki cevre aci arasindaki fark oldugu durumu kapsayacak sekilde genisletilebilir Merkezi O displaystyle O noktasi olan bir cember verildiginde cember uzerinde uc nokta V displaystyle V C displaystyle C ve D displaystyle D secilsin VC displaystyle VC ve VD displaystyle VD dogrularini cizelim DVC displaystyle angle DVC acisi bir cevre acidir Simdi VO displaystyle VO dogrusunu cizelim ve E displaystyle E noktasinda cemberle kesisecek ve O displaystyle O noktasini gececek sekilde uzatalim DVC displaystyle angle DVC acisi cember uzerindeki DC displaystyle DC yayini gorur Bu yayin icinde E displaystyle E noktasini icermedigini varsayalim E displaystyle E noktasi V displaystyle V noktasinin capa gore zittidir EVD displaystyle angle EVD ve EVC displaystyle angle EVC acilari da cevre acilardir ancak bu acilarin her ikisi de cemberin merkezinden gecen bir kenara sahiptir bu nedenle yukaridaki Bolum 1 deki teorem bunlara uygulanabilir Bu nedenle DVC EVC EVD displaystyle angle DVC angle EVC angle EVD o zaman ps0 DVC displaystyle psi 0 angle DVC ps1 EVD displaystyle psi 1 angle EVD ps2 EVC displaystyle psi 2 angle EVC olsun boylece ps0 ps2 ps1 3 displaystyle psi 0 psi 2 psi 1 qquad qquad 3 OC displaystyle OC ve OD displaystyle OD dogrularini cizelim EOD displaystyle angle EOD ve EOC displaystyle angle EOC acilari gibi DOC displaystyle angle DOC acisi da merkezi bir acidir ve DOC EOC EOD displaystyle angle DOC angle EOC angle EOD 80 DOC displaystyle theta 0 angle DOC 81 EOD displaystyle theta 1 angle EOD 82 EOC displaystyle theta 2 angle EOC olsun boylece 80 82 81 4 displaystyle theta 0 theta 2 theta 1 qquad qquad 4 Birinci bolumden biliyoruz ki 81 2ps1 displaystyle theta 1 2 psi 1 81 2ps1 displaystyle theta 1 2 psi 1 ve su 82 2ps2 displaystyle theta 2 2 psi 2 Bu sonuclarin denklem 4 ile birlestirilmesi 80 2ps2 2ps1 displaystyle theta 0 2 psi 2 2 psi 1 bu nedenle denklem 3 ile asagidaki ifadeye ulasilir 80 2ps0 displaystyle theta 0 2 psi 0 Sonuc Benzer bir argumana gore bir kiris ile onun kesisme noktalarindan birinde teget dogrusu arasindaki aci kirisin kapsadigi merkezi acinin yarisina esittir Ayrica bkz UygulamalarCevre aci teoremi duzlemin temel Oklid geometrisinin bircok ispatinda kullanilir Teoremin ozel bir durumu bir capin kapsadigi acinin her zaman 90 displaystyle 90 circ yani bir dik aci oldugunu belirten Thales teoremidir Teoremin bir sonucu olarak zit acilarinin toplami 180 displaystyle 180 circ dir ve tersine bunun dogru oldugu herhangi bir dortgen bir cember icerisine cizilebilir Baska bir ornek olarak cevre aci teoremi bir cembere gore ile ilgili birkac teorem icin temel olusturur Dahasi iki kiris bir cember icinde kesistiginde parcalarinin uzunluklarinin carpimlarinin esit oldugunu kanitlamaya izin verir Elipsler hiperboller ve paraboller icin cevre aci teoremleriCevre aci teoremleri elipsler hiperboller ve paraboller icin de mevcuttur Temel farklar bir acinin olcumleridir Bir aci bir cift kesisen cizgi olarak kabul edilir Elips Hiperbol ParabolKaynakca 1990 Excursions in Geometry Dover ss 17 23 ISBN 0 486 26530 7 Gellert W Kustner H Hellwich M Kastner H 1977 The VNR Concise Encyclopedia of Mathematics New York Van Nostrand Reinhold s 172 ISBN 0 442 22646 2 Moise Edwin E 1974 Elementary Geometry from an Advanced Standpoint 2 bas Reading Addison Wesley ss 192 197 ISBN 0 201 04793 4 Dis baglantilarEric W Weisstein Inscribed Angle MathWorld 11 Mayis 2009 tarihinde kaynagindan arsivlendi cut the knot org 15 Nisan 2003 tarihinde kaynagindan arsivlendi 30 Ekim 2006 tarihinde kaynagindan arsivlendi etkilesimli animasyon ile 30 Ekim 2006 tarihinde kaynagindan arsivlendi etkilesimli animasyon ile 30 Ekim 2006 tarihinde kaynagindan arsivlendi etkilesimli animasyon ile bookofproofs org 11 Temmuz 2020 tarihinde kaynagindan arsivlendi
 AzÉrbaycanca
AzÉrbaycanca ĐДлаŃŃŃĐșŃ
ĐДлаŃŃŃĐșŃ Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana æ„æŹèȘ
æ„æŹèȘ ÒĐ°Đ·Đ°Ò
ÒĐ°Đ·Đ°Ò Lietuvos
Lietuvos Nederlands
Nederlands PortuguĂȘs
PortuguĂȘs Đ ŃŃŃĐșĐžĐč
Đ ŃŃŃĐșĐžĐč à·à·à¶à·à¶œ
à·à·à¶à·à¶œ àčàžàžàčàžàžą
àčàžàžàčàžàžą TĂŒrkçe
TĂŒrkçe ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ°
ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ° äžćäșș
äžćäșș United State
United State Afrikaans
Afrikaans























