Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Alef sayıları, matematikte, daha ayrıntılı söylemek gerekirse kümeler teorisinde, iyi sıralı olabilen sonsuz kümelerin kardinalitesini göstermek için kullanılan sayılardır. Alef sayısı ismini sembolünden, İbranice alef harfinden alır. Bazı eski matematik kitaplarında yanlışlıkla alef sembolü ters basılmıştır.
Doğal sayılar kümesinin kardinalitesi ℵ0'dır (alef sıfır diye okunur), ondan sonraki kardinalite ise ℵ1 yani alef 1'dir, ondan sonra ℵ2 ve bu şekilde devam eder. Bu şekilde devam edilerek her a ordinal sayısı için bir ℵa kardinal sayısı bulmak mümkündür.
Fikir ve notasyon Georg Cantor'a aittir, kendisi sonsuz kümelerin değişik kardinalitelere sahip olabileceğini keşfetmiştir.
Alef sayıları genellikle cebir ve kalkülüste bulunan sonsuzluktan (∞) farklıdır. Alefler kümelerin büyüklüklerini ölçer, sonsuzluk ise genellikle fonksiyonlarda ve serilerde "sonsuza yaklaşır" denildiğinde reel sayılar doğrusunun sınırı olarak, genişletilmiş reel sayılar doğrusunda ise uç nokta olarak ifade edilir.
Alef sıfır
Alef sıfır doğal sayılar kümesinin kardinalitesidir (büyüklüğü). Alef sıfır en küçük sonsuz sayıdır. Sonsuz kardinal sayılar dizisinin ilk üyesidir. ℵ0 sembolü ile gösterilir.
ℵ0 doğal sayılar kümesinin kardinalitesidir ve sonsuz bir kardinaldir. Bütün ordinallerin kümesinin kardinalitesi de ki buna ω veya ω0 denir, (burada ω Yunan alfabesinden küçük omega harfidir) ℵ0'dır. Bir kümenin kardinalitesi ancak ve ancak sayılabilir sonsuzlukta ise ℵ0'dır, bu da küme ile doğal sayılar kümesi arasında bir birebir örten fonksiyon olduğu anlamına gelir. Bu kümelere örnek olarak şunlar verilebilir:
- Tüm tam kare sayıların kümesi, tüm kübik sayıların kümesi, tüm dördün kuvvetlerinin kümesi, ...
- Tüm mükemmel kuvvetli sayıların kümesi, tüm asal kuvvetli sayıların kümesi,
- Tüm çift sayıların kümesi, tüm tek sayıların kümesi,
- Tüm asal sayıların kümesi, tüm asal olmayan sayıların kümesi,
- Tüm tam sayıların kümesi,
- Tüm rasyonel sayıların kümesi,
- Tüm inşa edilebilen sayıların kümesi,
- Tüm cebirsel sayıların kümesi,
- Tüm tanımlanabilir sayıların kümesi,
- Tüm sınırlı bir uzunluğa sahip ikili dizilerin kümesi ve
- Bir sınırsız kümeye ait tüm sınırlı alt kümelerin kümesi.
ω,ω+1,ω*2,ω2,ωω gibi sonsuz ordinaller de sayılabilir sonsuzlukta kümelerle çalışır. Örneğin, ordinalitesi 2ω olan ve bütün pozitif tek sayılardan sonra bütün pozitif çift sayıların gelmesiyle oluşan
{1,3,5,7,9,...,2,4,6,8,10...}
kümesi kardinalitesi ℵ0 olan doğal sayılar kümesinin bir dizilişidir.
Alef bir
Alef bir, doğal sayılar kümesinin kuvvet kümesi'nin (doğal sayılar kümesinin elemanları ile oluşturulabilecek tüm kümelerin kümesi) kardinalitesidir (büyüklüğü).
ℵ1 bütün sayılabilen ordinal sayıların kümesinin kardinalitesidir ve sayılamaz sonsuzluktadır. Bu yüzden ℵ1, ℵ0'dan farklıdır. ℵ1'in tanımına göre (Zermelo-Frankel küme teorisine göre, seçim aksiyomu olmadan dikkate alınırsa), ℵ0 ile ℵ1 arasında hiçbir kardinal sayı yoktur. Seçim aksiyomu kullanılırsa, ℵ1 in en küçük ikinci sonsuz kardinal sayı olduğu kanısına ulaşılabilir.
Süreklilik hipotezi
Reel sayılar kümesinin kardinalitesi ()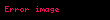 
dir. Alef sayıların arasında bu sayının hangi aralıkta olduğu ZFC (seçim aksiyomu olmadan Zermelo-Frankel küme teorisi) kullanılarak belirlenemez. Fakat ZFC kullanılarak süreklilik hipotezinin şu eşitlik anlamına geldiği bulunabilir:
Süreklilik hipotezine göre tam sayılar kümesinin kardinalitesi ile reel sayılar kümesinin kardinalitesi arasında kardinalite yoktur. Süreklilik hipotezi ZFC'den bağımsızdır: aksiyom sistemine bakılarak ne doğruluğu ispatlanabilir ne de yanlışlığı ispatlanabilir.
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Alef sayilari matematikte daha ayrintili soylemek gerekirse kumeler teorisinde iyi sirali olabilen sonsuz kumelerin kardinalitesini gostermek icin kullanilan sayilardir Alef sayisi ismini sembolunden Ibranice alef harfinden alir Bazi eski matematik kitaplarinda yanlislikla alef sembolu ters basilmistir Alef sifir en kucuk sonsuz nicel sayi Dogal sayilar kumesinin kardinalitesi ℵ0 dir alef sifir diye okunur ondan sonraki kardinalite ise ℵ1 yani alef 1 dir ondan sonra ℵ2 ve bu sekilde devam eder Bu sekilde devam edilerek her a ordinal sayisi icin bir ℵa kardinal sayisi bulmak mumkundur Fikir ve notasyon Georg Cantor a aittir kendisi sonsuz kumelerin degisik kardinalitelere sahip olabilecegini kesfetmistir Alef sayilari genellikle cebir ve kalkuluste bulunan sonsuzluktan farklidir Alefler kumelerin buyukluklerini olcer sonsuzluk ise genellikle fonksiyonlarda ve serilerde sonsuza yaklasir denildiginde reel sayilar dogrusunun siniri olarak genisletilmis reel sayilar dogrusunda ise uc nokta olarak ifade edilir Alef sifirAlef sifir dogal sayilar kumesinin kardinalitesidir buyuklugu Alef sifir en kucuk sonsuz sayidir Sonsuz kardinal sayilar dizisinin ilk uyesidir ℵ0 sembolu ile gosterilir ℵ0 dogal sayilar kumesinin kardinalitesidir ve sonsuz bir kardinaldir Butun ordinallerin kumesinin kardinalitesi de ki buna w veya w0 denir burada w Yunan alfabesinden kucuk omega harfidir ℵ0 dir Bir kumenin kardinalitesi ancak ve ancak sayilabilir sonsuzlukta ise ℵ0 dir bu da kume ile dogal sayilar kumesi arasinda bir birebir orten fonksiyon oldugu anlamina gelir Bu kumelere ornek olarak sunlar verilebilir Tum tam kare sayilarin kumesi tum kubik sayilarin kumesi tum dordun kuvvetlerinin kumesi Tum mukemmel kuvvetli sayilarin kumesi tum asal kuvvetli sayilarin kumesi Tum cift sayilarin kumesi tum tek sayilarin kumesi Tum asal sayilarin kumesi tum asal olmayan sayilarin kumesi Tum tam sayilarin kumesi Tum rasyonel sayilarin kumesi Tum insa edilebilen sayilarin kumesi Tum cebirsel sayilarin kumesi Tum tanimlanabilir sayilarin kumesi Tum sinirli bir uzunluga sahip ikili dizilerin kumesi ve Bir sinirsiz kumeye ait tum sinirli alt kumelerin kumesi w w 1 w 2 w2 ww gibi sonsuz ordinaller de sayilabilir sonsuzlukta kumelerle calisir Ornegin ordinalitesi 2w olan ve butun pozitif tek sayilardan sonra butun pozitif cift sayilarin gelmesiyle olusan 1 3 5 7 9 2 4 6 8 10 kumesi kardinalitesi ℵ0 olan dogal sayilar kumesinin bir dizilisidir Alef birAlef bir dogal sayilar kumesinin kuvvet kumesi nin dogal sayilar kumesinin elemanlari ile olusturulabilecek tum kumelerin kumesi kardinalitesidir buyuklugu ℵ1 butun sayilabilen ordinal sayilarin kumesinin kardinalitesidir ve sayilamaz sonsuzluktadir Bu yuzden ℵ1 ℵ0 dan farklidir ℵ1 in tanimina gore Zermelo Frankel kume teorisine gore secim aksiyomu olmadan dikkate alinirsa ℵ0 ile ℵ1 arasinda hicbir kardinal sayi yoktur Secim aksiyomu kullanilirsa ℵ1 in en kucuk ikinci sonsuz kardinal sayi oldugu kanisina ulasilabilir Sureklilik hipoteziReel sayilar kumesinin kardinalitesi 2ℵ0 displaystyle 2 aleph 0 dir Alef sayilarin arasinda bu sayinin hangi aralikta oldugu ZFC secim aksiyomu olmadan Zermelo Frankel kume teorisi kullanilarak belirlenemez Fakat ZFC kullanilarak sureklilik hipotezinin su esitlik anlamina geldigi bulunabilir 2ℵ0 ℵ1 displaystyle 2 aleph 0 aleph 1 Sureklilik hipotezine gore tam sayilar kumesinin kardinalitesi ile reel sayilar kumesinin kardinalitesi arasinda kardinalite yoktur Sureklilik hipotezi ZFC den bagimsizdir aksiyom sistemine bakilarak ne dogrulugu ispatlanabilir ne de yanlisligi ispatlanabilir Kaynakca 4 Kasim 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 17 Ocak 2020 web archive org 12 Mayis 2000 12 Mayis 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 6 Nisan 2022