Doğal sayılar

Doğal sayılar, ${\displaystyle \{1,2,3,4,5,6,7,...\}}$ şeklinde sıralanan tam sayılardır ve kimi tanımlamalara göre 0 sayısı da bu kümeye dâhil edilebilir. Aralarında standart 'nin de bulunduğu bazı tanımlar doğal sayıları 0 ile başlatır ve bu durum negatif olmayan tam sayılar için 0, 1, 2, 3, ... şeklinde bir karşılık bulurken, bazı tanımlamalar 1 ile başlamakta ve bu da pozitif tam sayılar için 1, 2, 3, ... şeklinde bir eşlenik oluşturur. Doğal sayıları sıfır olmadan ele alan metinlerde, sıfırın da dahil edildiği doğal sayılar bazen tam sayılar olarak adlandırılırken, diğer bazı metinlerde bu terim, negatif tam sayılar da dahil olmak üzere tam sayılar için kullanılmaktadır. Özellikle ilkokul seviyesindeki eğitimde, doğal sayılar, negatif tam sayıları ve sıfırı dışlamak ve saymanın ayrık yapısını, gerçek sayıların bir karakteristiği olan ölçümün sürekliliğiyle karşıtlık oluşturmak amacıyla sayma sayıları olarak adlandırılabilir.

Doğal sayılar saymak için kullanılabilir: bir elma; iki elma, bir elmaya bir elma eklenmesidir; üç elma, iki elmaya bir elma eklenmesidir, ...

Doğal sayılar, "masa üzerindeki bozuk paraların sayısı 'altıdır'" şeklindeki ifadelerde sayma amaçlı kullanıldığında, kardinal sayı olarak adlandırılan bir işlevi üstlenirler. Bunun yanı sıra, "bu şehir, ülke çapındaki 'üçüncü' en büyük şehirdir" şeklindeki ifadelerde sıralama amaçlı kullanıldıklarında ise, sıral sayı olarak adlandırılan farklı bir işlevi yerine getirirler. Zaman zaman doğal sayılar, matematiksel anlamda sayısal özelliklere sahip olmayan, spor dallarındaki forma numaraları gibi, olarak adlandırılan etiketleme amaçları için de tercih edilirler.

Doğal sayılar, genellikle N sembolü ile gösterilen bir kümeyi teşkil ederler. Bu sayılar kümesi, doğal sayılar kümesinin ardışık genişlemeleriyle birçok farklı (sayı kümesinin) inşasına olanak sağlar: tamsayılar, doğal sayılar kümesine, henüz dahil edilmemişse bir olan 0 ve her bir sıfırdan farklı doğal sayı n için tanımlanan bir toplamının tersi −n ekleyerek oluşturulur; rasyonel sayılar, her bir sıfırdan farklı tam sayı n için bir ${\displaystyle 1/n}$ ekleyerek ve bu terslerin tam sayılar ile çarpımını da içerecek şekilde genişletilir; reel sayılar, rasyonel sayıların limitlerine ulaşan ile zenginleştirilerek elde edilir; karmaşık sayılar, reel sayılara eklenen bir −1'in karekökü ve bu karekökün toplamları ile çarpımları ile genişletilir; ve bu süreç böyle devam eder. Bu ardışık genişletme serisi, doğal sayıların diğer sayı sistemlerine kanonik bir şekilde gömülmesini sağlar.

Doğal sayılara ait özellikler, örneğin bölünebilirlik ve asal sayı dağılımı gibi konular, sayılar teorisi disiplininde ele alınmaktadır. Sayma ve sıralamaya dair meseleler, bölüntü ve enumeratif kombinatorik yöntemler gibi konular, kombinatorik çalışma alanında detaylı bir şekilde incelenmektedir.

Tarihçe

Antik köken

Belçika'da bulunan ve 'nde muhafaza edilip sergilenen İşango kemiği,, yaklaşık 20.000 yıl önce doğal sayıların aritmetiğiyle ilgili işlemlerde kullanıldığı düşünülen bir objedir.

Doğal sayıların gösterimi konusunda en temel yöntemlerden biri, parmakla sayma metoduyla parmakların kullanılmasıdır. Nesne başına bir eklemek de benzer şekilde ilkel bir yöntem olarak kabul edilir. İlerleyen zamanlarda, bir nesneler topluluğu, bir işareti silip topluluktan bir nesneyi ayırarak eşitlik, fazlalık veya eksiklik yönünden değerlendirilebilir.

Sayıları ifade etmek amacıyla rakamların kullanılması, soyutlama noktasında önemli bir ilerleme olarak görülür. Bu yaklaşım, büyük sayıların kaydedilmesi için sistemlerin oluşturulmasına imkan tanımıştır. Antik Mısır uygarlığı, 1, 10 ve 1 milyonu aşkın değerlere kadar olan 10'un katları için özgün hiyeroglifler barındıran kapsamlı bir sayı sistemi geliştirmiştir. Paris'teki Louvre müzesinde sergilenen ve M.Ö. 1500 yıllarına tarihlenen bir Karnak taş oyması, 276 sayısını iki yüz, yedi on ve altı birim olarak temsil ederken, 4,622 sayısı için de benzer bir gösterim kullanılmıştır. Babil uygarlığı ise, 1 ve 10 için özel semboller kullanılarak kurulan ve altmışlık bir tabana dayanan bir basamak sistemine sahipti; bu sistemde altmış için kullanılan sembol, bir için kullanılan sembolle aynıydı ve değeri bağlamdan çıkarılabiliyordu.

0 sayısının, kendi özgün sayısal simgesiyle birlikte bir sayı olarak değerlendirilmesi fikrinin ortaya çıkışı, nispeten daha geç bir gelişmedir. Basamak notasyonunda bir 0 rakamının kullanımı (diğer sayılar içinde) M.Ö. 700'lere dayanır ve bu uygulama Babilliler tarafından benimsenmiştir; bu basamak, sayının en son sembolü olacaksa kullanılmamıştır.Olmek ve Maya uygarlığı M.Ö. 1. yüzyılda 0'ı bağımsız bir sayı olarak kullanmışlardır, fakat bu kullanım Mezoamerika dışına yayılmamıştır. Modern dönemde bir 0 sayısal işaretinin kullanımı M.S. 628 yılında Hint matematikçi Brahmagupta ile başlamıştır. Ancak, 0 sayısı, M.S. 525 yılında ile başlayarak, Orta Çağ 'unda (Paskalya'nın tarihinin hesaplanması), bir sayısal işaret olmadan bir sayı olarak kullanılmıştır. Standart Roma rakamlarında 0 için bir sembol bulunmamaktadır; bunun yerine, Latince "hiçbiri" anlamına gelen nullus kelimesinden türetilen nulla (veya iyelik hali nullae) 0 değerini ifade etmek için kullanılmıştır.

Sayıların soyutlamalar ile sistematik olarak incelenmesi, genellikle Yunan filozoflar Pisagor ve Arşimet'e mal edilir. Bazı Yunan matematikçiler, sayı 1'i daha büyük sayılardan farklı olarak, bazen tam olarak bir sayı olarak bile değerlendirmemişlerdir.Euclid, bir birimi öncelikle tanımlayıp ardından bir sayıyı birimlerin çokluğu olarak tanımlamıştır; böylece onun tanımına göre bir birim bir sayı değildir ve benzersiz sayılar mevcut değildir (örneğin, belirsiz sayıda birimden herhangi iki birim bir 2 olarak kabul edilir). Ancak, hemen ardından gelen mükemmel sayı tanımında, Euclid 1'i diğer herhangi bir sayı gibi ele alır.

Sayılar üzerine bağımsız çalışmalar, aynı dönemlerde Hindistan, Çin ve Mezoamerika'da da yürütülmüştür.

Modern tanım

19. yüzyıl Avrupa'sında doğal sayılar kavramının esas mahiyeti üzerine matematiksel ve felsefi düzeyde tartışmalar gerçekleştirilmiştir. Henri Poincaré, aksiyomların yalnızca sonlu uygulamaları kapsamında ispatlanabileceğini ifade etmiş ve aynı işlemin belirsiz sayıda tekrarının zihinsel bir kavrayışla mümkün kılındığı sonucuna ulaşmıştır.Leopold Kronecker, kendi inancını "Tanrı tamsayıları yarattı, diğer her şey insanın eseridir" şeklinde özetlemiştir.

Yapılandırmacılar, matematiğin temelleri alanındaki mantıksal kesinliği artırma gereksinimini vurgulamışlardır. 1860'lar döneminde, doğal sayılar için özyinelemeli bir tanım önererek, bu sayıların aslında doğuştan gelmediğini, fakat tanımların bir ürünü olduğunu ifade etmiştir. İlerleyen zamanlarda, bu tip formal tanımların iki ayrı sınıfı geliştirilmiş; daha sonrasında ise, bu tanımların çoğu pratik uygulamada birbirine eşdeğer olarak kabul edilmiştir.

Doğal sayıların küme teorisiyle ilişkilendirilmesine yönelik tanımlamalar, Frege tarafından geliştirilmiştir. İlk etapta, Frege bir doğal sayıyı, belirli bir küme ile birebir korespondans kurabilen tüm kümelerin topluluğu olarak ifade etmiştir. Ancak, bu yaklaşım, Russell paradoksu da dahil olmak üzere çeşitli paradokslara sebebiyet vermiştir. Bu tür paradokslardan sakınmak amacıyla, tanımlama biçimi, bir doğal sayının özel bir küme olarak tanımlandığı ve herhangi bir kümenin, bu küme ile birebir korespondans kurabiliyorsa, söz konusu kümenin eleman sayısının bu sayı olduğu şeklinde modifiye edilmiştir.

İkinci kategori tanımlamalar, Charles Sanders Peirce tarafından ortaya konmuş, Richard Dedekind tarafından rafine edilmiş ve Giuseppe Peano tarafından detaylı bir şekilde ele alınmıştır; bu metodoloji günümüzde Peano aritmetiği olarak bilinmektedir. Bu yaklaşım, sıral sayıların özelliklerinin aksiyomatik bir çerçevede ele alınmasına dayanmaktadır: Her doğal sayının bir sonraki sayısı vardır ve sıfırdan farklı her doğal sayının benzersiz bir önceki sayısı vardır. Peano aritmetiği, birkaç zayıf küme teorisi sistemiyle eş tutarlılık gösterir. Bu sistemlerden biri, tersi ile değiştirilmiş ZFC sistemidir. ZFC'de kanıtlanabilir ancak Peano Aksiyomları kullanılarak kanıtlanamayan teoremler arasında bulunur.

Bu tanımlar ışığında, boş kümeyle özdeşleştirilen 0 sayısının doğal sayılar kümesine dahil edilmesi mantıklı bir yaklaşım olarak değerlendirilmektedir. Günümüzde küme teorisyenleri ve mantık bilimcileri arasında 0'ı doğal sayılar kümesine dahil etme eğilimi yaygındır. Matematikçilerin bir kısmı da bu uygulamayı benimserken, bilgisayar dilleri de genellikle döngü sayaçları, dizgi veya dizi elemanları gibi nesneleri saymaya sıfırdan başlamaktadır. Diğer yandan, birçok matematikçi, eski geleneği sürdürerek ilk doğal sayı olarak 1'i kabul etme eğilimindedir. Bu yaklaşım, özellikle gerçek analiz üzerine yazılmış metinlerde yaygındır.

Simgelem

Doğal sayılar kümesi, standart olarak N veya ${\displaystyle \mathbb {N} }$ ile ifade edilmektedir. Daha eski metinlerde, bu küme için bazen J simgesi tercih edilmiştir.

Doğal sayıların 0'ı kapsayıp kapsamadığı duruma göre değişiklik gösterebilir, bu yüzden atıfta bulunulan versiyonun hangisi olduğunu anlamak önem arz eder. Bu genellikle bağlamdan anlaşılır, fakat notasyonda bir alt ya da üst simge kullanımı ile de açıklanabilir. Örneğin:

• Sıfırsız doğal sayılar için: ${\displaystyle {1,2,...}=\mathbb {N} ^{*}=\mathbb {N} ^{+}=\mathbb {N} _{0}\smallsetminus {0}=\mathbb {N} _{1}}$
• Sıfır dahil doğal sayılar için: ${\displaystyle {0,1,2,...}=\mathbb {N} _{0}=\mathbb {N} ^{0}=\mathbb {N} ^{*}\cup {0}}$

Diğer bir yaklaşım olarak, doğal sayılar, tam sayılar kümesinin bir alt kümesini meydana getirdiklerinden (genellikle ${\displaystyle \mathbb {Z} }$ şeklinde ifade edilir), bu sayılar pozitif ya da negatif olmayan tam sayılar olarak da tanımlanabilirler. 0 sayısının dahil edilip edilmediğine dair muğlaklığı gidermek amacıyla, bazen pozitif tam sayılar için üst simge olarak "${\displaystyle *}$" veya "+" işareti, negatif olmayan tam sayılar için ise alt simge (veya üst simge) olarak "0" işareti kullanılır:

${\displaystyle {1,2,3,\dots }={x\in \mathbb {Z} :x>0}=\mathbb {Z} ^{+}=\mathbb {Z} {>0}}$

${\displaystyle {0,1,2,\dots }={x\in \mathbb {Z} :x\geq 0}=\mathbb {Z} ^{+}{0}=\mathbb {Z} _{\geq 0}}$

Özellikler

Bu bölüm, 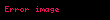${\displaystyle \mathbb {N} =\mathbb {N} _{0}=\mathbb {N} ^{*}\cup {0}}$ gösterimini esas alır.

Toplama işlemi

Doğal sayılar kümesi ${\displaystyle \mathbb {N} }$ ve her bir doğal sayıyı bir sonraki sayıya eşleyen ${\displaystyle S\colon \mathbb {N} \to \mathbb {N} }$ göz önünde bulundurulduğunda, doğal sayıların toplaması, a + 0 = a ve her a, b için a + S(b) = S(a + b) olacak şekilde özyinelemeli olarak tanımlanabilir. Bu durumda, a + 1 = a + S(0) = S(a+0) = S(a), a + 2 = a + S(1) = S(a+1) = S(S(a)) şeklinde ifade edilir ve bu dizilim devam eder. ${\displaystyle (\mathbb {N} ,+)}$ cebirsel yapısı, 0 kimlik elemanına sahip bir değişmeli monoiddir ve bu yapı, bir üreteç üzerinden serbest monoid özelliği gösterir. Toplamanın kısalma özelliğini de sağlayan bu değişmeli monoid, bir grup içerisine gömülebilir özelliktedir. Doğal sayıları kapsayan en minimal grup, tamsayılar grubudur.

Eğer 1, S(0) olarak tanımlanırsa, b + 1 = b + S(0) = S(b + 0) = S(b) olur. Bu, b + 1 ifadesinin, b sayısının ardılı olduğunu basitçe gösterir.

Toplama işlemi ileri doğru sayma işlemidir. Toplama işlemine katılan sayılara terim, işlemin sonucuna toplam denir. Toplama işlemi sayıların aynı basamakları arasında yapılır. Bu nedenle toplama işleminde sayılar aynı basamaklar alt alta gelecek şekilde yapılır.

Doğal sayılarda toplama aşağıdaki cebirsel kurallara uyar:

• Toplamsal birim öğe:

a + 0 = a

• Toplamanın değişme özelliği:

a + b = b + a

• Toplamanın birleşme özelliği:

(a + b) + c = a + (b + c)

• Toplamanın çarpma üzerine dağılma özelliği (sağdan dağılma):

(a + b)c = ac + bc

Bir a sayısını bir b sayısıyla toplamak, a sayısının b kere ardılını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse 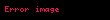${\displaystyle Ard(n)}$ gösterimi n sayısının ardılını ifâde etmek üzere, toplama aşağıdaki belitlerle tanımlanır:

1. ${\displaystyle a+0=a}$
2. ${\displaystyle a+Ard(b)=Ard(a+b)}$

Bu belitlerden yola çıkarak ardıllık işlemini toplama cinsinden göstermek mümkündür: 2. belitte b=0 seçilirse

${\displaystyle a+Ard(0)=ard(a+0)}$

sıfırın ardılı birdir, o halde,

${\displaystyle Ard(a)=a+1}$

olduğu kolaylıkla görülür.

Çarpma işlemi

Toplamanın tanımlanmış olması göz önüne alındığında, çarpma işlemi ${\displaystyle \times }$, a × 0 = 0 ve a × S(b) = (a × b) + a olacak şekilde tanımlanabilir. Bu tanım, ${\displaystyle (\mathbb {N} ^{*},\times )}$ yapısnı, etkisiz elemanı 1 olan serbest değişmeli bir monoid yapısına çevirir; bu monoidin üreteçler kümesi, asal sayılar kümesidir.

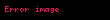
Çarpma işlemi art arda toplama işlemidir. Çarpma işlemine katılan sayılara çarpan, işlemin sonucuna çarpım denir.

Doğal sayılarda çarpma aşağıdaki cebirsel kurallara uyar:

• Çarpımsal birim öge:

a1 = a

• Çarpmanın değişme özelliği:

ab = ba

• Çarpmanın birleşme özelliği

(ab)c = a(bc)

• Çarpmanın toplama üzerine dağılma özelliği (soldan dağılma):

c(a + b) = ca + cb

Bir a sayısını bir b sayısıyla çarpmak, a sayısının b kere toplamını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse 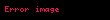${\displaystyle Ard(n)}$ gösterimi n sayısının ardılını ifade etmek üzere, çarpma aşağıdaki belitlerle tanımlanır:

1. ${\displaystyle a1=a}$
2. ${\displaystyle a\,Ard(b)=ab+a}$

Toplama ve çarpma işlemleri arasındaki ilişki

Toplama ve çarpma işlemleri birbiriyle uyumludur, bu durum dağılma özelliği ile ifade edilir: a × (b + c) = (a × b) + (a × c). Toplama ve çarpmanın bu özellikleri, doğal sayıları bir değişmeli (İngilizce: semiring; aynı zamanda rig olarak da bilinir) örneği yapar. Yarhalkalar, çarpmanın mutlaka değişmeli olmadığı doğal sayıların cebirsel bir genelleştirmesidir. Toplam terslerinin olmaması, ki bu ${\displaystyle \mathbb {N} }$'in çıkarma işlemi altında olmadığına eşdeğerdir (yani, bir doğal sayıdan diğer bir doğal sayıyı çıkarmak her zaman başka bir doğal sayı sonucu vermez), ${\displaystyle \mathbb {N} }$'in bir halka olmadığı anlamına gelir; bunun yerine bir .

Doğal sayılar "0 hariç" alınırsa ve "1'den başlayarak" kabul edilirse, + ve × tanımları yukarıdaki gibi olur, ancak a + 1 = S(a) ve a × 1 = a ile başlarlar. Ayrıca, ${\displaystyle (\mathbb {N^{*}} ,+)}$'ın kimlik elemanı bulunmamaktadır.

Sıralama

Bu bölümde, ab gibi yan yana getirilmiş değişkenler a × b çarpımını belirtir ve standart işlem sırası varsayılmaktadır.

Doğal sayılar üzerinde bir a ≤ b şeklinde tanımlanır, ancak ve ancak a + c = b olacak şekilde başka bir doğal sayı c varsa. Bu sıralama, aşağıdaki anlamda aritmetik işlemler ile uyumludur: eğer a, b ve c doğal sayılarsa ve a ≤ b ise, o zaman a + c ≤ b + c ve ac ≤ bc olur.

Doğal sayıların önemli bir özelliği, iyi sıralı olmalarıdır: doğal sayılardan oluşan her boş olmayan kümenin en küçük bir elemanı vardır. İyi sıralı kümeler arasındaki rütbe bir sıral sayı ile ifade edilir; doğal sayılar için bu, ω (omega) olarak belirtilir.

Doğal sayıların sıralanmasına en büyük basamaktan başlanır. Aynı basamakta büyük rakam bulunan sayı diğerinden büyüktür.

İki sayının yüz milyonlar basamaklarında eşit rakamlar bulunuyor. Bu nedenle karşılaştırma bir sonraki basamak olan on milyonlar basamaklarında yapılır. Bu basamaklarda 9 > 8 olduğundan 894.125.067 > 887.954.700 yazılır. “ 894.125.067 büyüktür 887.954.700 şeklinde okunur.”

${\displaystyle \mathbb {N} =\{0,1,2,3,4,5,6,7,...\}}$ Doğal Sayılar Kümesinde; iki doğal sayının toplamı yine bir doğal sayı olur.

Bölme

Bu bölümde, ab gibi yan yana getirilmiş değişkenler a × b çarpımını gösterir ve standart işlem sırası kabul edilir.

Genellikle bir doğal sayıyı başka bir doğal sayıya böldüğümüzde sonuç olarak doğal bir sayı elde edilemese de, kalanlı bölme veya Öklid bölmesi işlemi bir alternatif olarak kullanılabilir: b ≠ 0 olmak üzere herhangi iki doğal sayı a ve b için :${\displaystyle a=bq+r{\text{ ve }}r<b}$ şeklinde olacak q ve r doğal sayıları vardır.

Sayı q bölme işleminin bölümü olarak, r ise kalan olarak adlandırılır. a'yı b'ye böldüğümüzde elde edilen q ve r sayıları a ve b tarafından özebir şekilde belirlenir. Bu Öklid bölmesi, sayılar teorisinde birçok diğer özellik (bölünebilirlik), algoritmalar (örneğin, Öklid algoritması) ve fikirler için temel taşını oluşturur.

Cebirsel özellikler

Doğal sayılar kümesinde tanımlanmış olan toplama (+) ve çarpma (×) işlemleri, aşağıda sıralanan bir dizi cebirsel özelliği sağlar:

• Herhangi iki doğal sayı a ve b için, toplama ve çarpma işlemleri altında (İngilizce closure) gözlenir; yani, a + b ve a × b ifadeleri yine doğal sayılardır.
• Birleşme özelliği: Herhangi bir a, b ve c doğal sayısı üzerinde gerçekleştirilen toplama ve çarpma işlemleri, birleşme özelliğine uygundur; bu da, a + (b + c) = (a + b) + c ve a × (b × c) = (a × b) × c şeklinde ifade edilir.
• Değişme özelliği: İki doğal sayı a ve b arasındaki toplama ve çarpma işlemleri, değişme kuralına uyar; yani, a + b = b + a ve a × b = b × a eşitlikleri geçerlidir.
• Doğal sayılar kümesi içerisinde, her a doğal sayısı için, a + 0 = a ve a × 1 = a olacak şekilde birim elemanların varlığı kabul edilebilir.
  • Eğer doğal sayılar sıfırı dışlayarak ve bir ile başlayarak ele alınırsa, her a doğal sayısı için çarpma işlemi altında birim elemanın varlığı geçerli olmakla birlikte, toplama işlemi altında birim elemanın varlığı özelliği karşılanmaz.
• Dağılma özelliği: Çarpma işleminin toplama işlemi üzerine dağılma özelliği, herhangi üç doğal sayı a, b ve c için, a × (b + c) = (a × b) + (a × c) biçiminde ifade edilir.
• : eğer a ve b doğal sayıları için a × b = 0 ise, bu durumda a = 0 veya b = 0 olmalıdır (veya her ikisi de).
  • Doğal sayılar kümesi sıfırı dışlayarak ve bir ile başlayarak ele alındığında, sıfırdan farklı sıfır bölenin bulunmaması ilkesi geçerliliğini yitirir.

Sayı değeri

Bir doğal sayının rakamlarının belirttiği değere rakamların sayı değeri denir. Doğal sayının rakamlarının toplamına rakamların sayı değerleri toplamı denir.

Basamak değeri

9 basamaklı bir doğal sayının basamaklarının

• Birler basamağının basamak değeri :1
• Onlar basamağının basamak değeri :10
• Yüzler basamağının basamak değeri :100
• Binler basamağının basamak değeri :1.000
• On binler basamağının basamak değeri :10.000
• Yüz binler basamağının basamak değeri :100.000
• Milyonlar basamağının basamak değeri :1.000.000
• On milyonlar basamağının basamak değeri :10.000.000
• Yüz milyonlar basamağının basamak değeri :100.000.000

Onlu sayma düzeninde bir basamağın değeri sağındaki basamağın 10 katıdır.

Bir rakamın basamak değeri o rakam ile rakamın yazıldığı basamağın çarpımıyla bulunur.

12345 sayısındaki 2 nin basamak değeri 2 (sayı değeri) ve 1000 (basamak değeri) çarpılarak 2 × 1000 = 2000 şeklinde bulunur.

Genellemeler

Doğal sayıların iki temel uygulaması, sayma ve sıralama, onlardan neşet eden iki mühim genelleştirmeye zemin hazırlar: nicel (kardinal) sayılar ve sıral (ordinal) sayılar.

• Bir sonlu topluluğun niceliksel büyüklüğü, doğal sayılar yardımıyla tanımlanabilir; daha açık bir deyişle, bir topluluğun büyüklüğünü ölçen bir nicel sayı, sonsuz topluluklar için dahi uygun bir metriktir. Nicel sayıların sıralaması genelde, boş küme ${\displaystyle \emptyset }$ 'yi dikkate alacak biçimde, sıfırdan başlatılır. Bu "büyüklük" tanımı, iki topluluğun ancak ve ancak aralarında bir bijeksiyon mevcut ise sahip olduğunu varsayan topluluklar arası fonksiyonel ilişkilere istinaden şekillenmiştir. Doğal sayılar topluluğu ve bu topluluğun bijektif dönüşümü, sayılabilir sonsuz olarak nitelendirilir ve açısından (alef-sıfır) (ℵ₀) değerine sahiptir.
• Doğal sayılar, "birinci", "ikinci", "üçüncü" gibi ifadelerle dilbilimsel sıral sayılar olarak işlev görürler. Sıral sayıların sıralanışı genelde, boş küme ${\displaystyle \emptyset }$ 'nin sıralama türünü dikkate alacak biçimde, başlangıç noktası olarak sıfırı alır. Bu yöntemle, tam sıralı sonlu bir kümenin unsurlarına ve herhangi bir iyi sıralı sayılabilir sonsuz kümenin unsurlarına değerler atanabilir. Bu atama işlemi, sayılabilirliğin ötesinde bir kardinaliteye sahip genel iyi sıralamalar için genelleştirilebilir ve böylece sıral sayılar elde edilir. Bir sıral sayı, iyi sıralı bir kümenin "büyüklüğü"nü, kardinalite anlayışından farklı bir bakış açısıyla açıklamak için de kullanılabilir: iki iyi sıralı küme arasında bir (yalnızca bir bijeksiyondan daha fazlası) mevcut ise, bu kümeler aynı sıral sayıya sahiptirler. Doğal sayı olmayan ilk sıral sayı ω ile ifade edilir; bu, doğal sayılar kümesinin kendisinin de sıral sayısıdır.

Kardinalite değeri ℵ₀ olan sırallar arasında, en küçük olanı (diğer bir deyişle, ℵ₀ için ) ω olarak belirlenmiştir. Bununla birlikte, kardinal numarası ℵ₀ olan birçok iyi düzenlenmiş kümenin, sıral numarası ω'dan daha yüksek değerlere ulaşmaktadır.

ve iyi düzenlenmiş kümeler söz konusu olduğunda, sıral ve nicel sayılar arasındaki ilişki, bir-bir karşılıklılığı şeklinde tezahür eder; dolayısıyla, her iki tür sayı da, ilgili kümenin unsurlarının toplam sayısını yansıtan ve bu sayede kümenin eleman sayısı ile eş değer tutulan aynı doğal sayı ile ifade edilebilir. Söz konusu sayı, aynı zamanda, daha geniş bir sonlu veya bir sonsuz dizi içerisinde bir ögenin konumunu belirtmek için de işlev görür.

Skolem tarafından 1933 yılında ortaya konan, Peano Aritmetiği'nin (yani, birinci mertebeden Peano aksiyomlarının) gerekliliklerini karşılayan sayılabilir bir mevcuttur. ise, sıradan doğal sayılardan aracılığıyla türetilebilen ve sayılamaz nitelikte olan bir modeli temsil eder.

Formel tanımlamalar

Doğal sayıların formel bir biçimde tanımlanmasına yönelik iki yaygın yöntem mevcuttur. Bunlardan birincisi, Giuseppe Peano'nun adıyla anılan ve birkaç temel aksiyom üzerine kurulu Peano aksiyomlarına dayalı adı verilen bağımsız bir içerir.

İkinci tanımlama, küme teorisinin prensiplerine istinaden gerçekleştirilir. Bu yaklaşım, doğal sayıları, özel kümeler olarak tanımlar. Daha belirgin bir açıklamayla, her bir doğal sayı n, diğer kümelerin unsurlarının sayımına olanak tanıyan, açık bir biçimde belirlenmiş bir küme olarak ifade edilir; "bir küme S n adet unsura sahiptir" ifadesi, n ile S kümeleri arasında bir bire bir denklik olduğunu gösterir.

Doğal sayıların tanımında başvurulan kümeler, Peano aksiyomlarını tatmin eder. Bu, Peano aritmetiğinde ifade edilip ispatlanabilecek her teoremin, küme teorisi çerçevesinde de ispatlanabilir olduğunu gösterir. Fakat, her iki tanımın eşdeğer olmadığı da bir gerçektir; zira Peano aritmetiği diliyle tanımlanıp küme teorisiyle ispatlanabilen ancak Peano aritmetiği dahilinde ispatlanamayan teoremler mevcuttur. Bu bağlamda muhtemel bir örnek Fermat'ın Son Teoremi'dir.

Tam sayıların, Peano aksiyomlarını karşılayan kümeler şeklinde tanımlanması, küme teorisi bağlamında Peano aritmetiğinin bir oluşturur. Bu durumun önemli bir neticesi olarak, eğer küme teorisi tutarlı bir yapıya sahipse (genel kabule göre), bu durum Peano aritmetiğinin de tutarlı olduğunu gösterir. Diğer bir ifadeyle, Peano aritmetiğinde bir çelişki ispatlanabilirse, bu durum küme teorisinin de çelişkili olduğunu ima eder ve küme teorisinin tüm teoremleri hem doğru hem de yanlış kabul edilir.

Peano aksiyomları

Beş Peano aksiyomları şunlardır:

• Sıfır, doğal sayılar kümesinin bir elemanıdır.
• Her bir doğal sayı için, bu sayıyı takip eden bir sonraki değer de doğal sayılar kümesine aittir.
• Hiçbir doğal sayının bir sonraki değeri olarak sıfır (0) kabul edilmez.
• Eğer iki doğal sayı birbirinden farklı ise, bu sayıların her birini takip eden sonraki değerler de birbirinden farklıdır.
• Eğer bir özellik sıfır (0) değeri için doğru ise ve herhangi bir n doğal sayısı için bu özellik geçerliyse, bu özelliğin n sayısını takip eden sayı için de geçerli olması durumunda, söz konusu özellik tüm doğal sayılar için geçerlidir.

Bu aksiyomlar, Peano'nun yayımladığı orijinal aksiyomlar olmamakla birlikte, onun şerefine bu isimle anılmaktadır. Peano aksiyomlarının çeşitli versiyonlarında, bazen 0'ın yerine 1 konulmaktadır. Geleneksel aritmetik çerçevesinde, ${\displaystyle x}$ elemanının ardılı ${\displaystyle x+1}$ olarak tanımlanır.

ZFC tanımı

Zermelo-Freankel küme kuramı doğal sayılar, sıral sayılarıyla inşa edilebilir. Buna göre her sayı temelde bir kümedir. Eğer sıfır boşküme olarak tanımlanırsa ve her n sayının ardılı, ${\displaystyle n^{+}}$, n${\displaystyle \cup }${n} olarak verilirse, doğal sayılar inşa edilmiş olur.

${\displaystyle 0=\emptyset }$

${\displaystyle n^{+}=n\cup \{n\}}$

Bu tanım doğal sayıların yinelgen bir yapıda olduğunu da belirtmiş olur. Bu yinelgen tanımla sayılar,

0={}

1={0}

2={0,1}

3={0,1,2}

...

n+1={0,1,...,n}

Bu tanımda iki doğal sayının eşitliği sayıların öğe sayısına dayanır.

Russell'ın farklı bir tanımı daha genel görünebilir: 0 DOĞAL SAYIDIR

${\displaystyle 0={\emptyset }}$ (sıfır, hiç öğesi olmayan tüm kümelerin kümesi)

${\displaystyle n^{+}=\{x\cup \{y\}\,|\,x\in n\,{\text{ve}}\,y\not \in x\}}$ (n'nin ardılı, öğe sayısı n olan tüm kümelerin kümesi)

Ne var ki bu tanım belitsel küme kuramlarında geçerli değildir, çünkü bir sayı, küme olamayacak kadar büyük topluluklar olmak zorunda kalıyor. Ancak gibi kuramlarda geçerlidir.

Küme Teorisel Tanım

Sezgisel olarak, n doğal sayısı, n sayıda elemana sahip tüm kümelerin paylaştığı ortak bir özelliktir. Bu bağlamda, n'nin "birbirleriyle bire bir denklik kurulabilir" ilişkisi çerçevesinde bir olarak tanımlanması doğal bir yaklaşım olarak düşünülebilir. Ne var ki, bu yöntem küme teorisi içerisinde uygulanabilir değildir, zira bu tür bir denklik sınıfı bir küme oluşturmayacaktır (Russell paradoksu sebebiyle). Standart çözüm, n sayıda elemana sahip özgün bir küme belirlemek ve bu kümeyi doğal sayı n olarak adlandırmaktır.

Aşağıda sunulan tanım, ilk kez John von Neumann tarafından yayımlanmıştır, fakat Levy, bu düşüncenin Zermelo'nun 1916 yılında yayımlanmamış eserlerine dayandığını ifade etmektedir. Bu tanımın için de bir sıral sayı tanımı olarak uygulanabilir olması dolayısıyla, burada incelenen kümeler zaman zaman olarak isimlendirilmektedir.

Tanım aşağıdaki adımlarla gerçekleştirilir:

• :${\displaystyle 0=\emptyset }$, boş küme olarak tanımlanır.
• Bir a kümesinin ardılı S(a) olarak, S(a) = a ∪ {a} biçiminde belirlenir.
• gereği, 0 değerini içeren ve ardıl fonksiyonu altında olan kümeler bulunmaktadır. Bu tür kümeler indüktif küme olarak ifade edilir. Tüm indüktif kümelerin kesişimi, yine bir indüktif küme oluşturur.
• Bu kesişim, doğal sayılar kümesini oluşturur.

Doğal sayıların Peano aksiyomlarını sağladığı kontrol edilebilir.

Bu tanımla birlikte, bir doğal sayı n verildiğinde, "bir küme S, n elemanına sahiptir" cümlesi formel olarak "n ile S arasında bir bijeksiyon bulunur" şeklinde tanımlanabilir. Bu, S'nin elemanlarının sayılması işlemini formalize eder. Ayrıca, n ≤ m ifadesi, yalnızca n'nin m'nin bir alt kümesi olduğunda geçerlidir. Diğer bir deyişle, küme içerme ilişkisi, doğal sayılar üzerindeki alışılagelmiş tanımlar. Bu sıralama bir iyi sıralamadır.

Tanım gereği, her bir doğal sayı, kendisinden küçük olan tüm doğal sayıların topluluğuna denktir. Bu kavram, von Neumann'ın sıralı sayılar tanımı aracılığıyla kullanılarak genişletilebilir ki bu, sonsuz olanlar da dâhil olmak üzere tüm sıral sayıların tanımlanmasını sağlar: "Her bir sıralı sayı, kendisinden küçük olan sıralı sayıların iyi bir şekilde sıralanmış topluluğudur."

Sonsuzluk aksiyomunun geçerli olmadığı finitist yaklaşımlarda, doğal sayılar bir küme olarak kabul edilmeyebilir. Bununla birlikte, doğal sayılar yukarıda açıklandığı üzere bireysel olarak tanımlanabilir ve Peano aksiyomlarını tatmin etmeye devam ederler.

Diğer küme teorik yapılanmalar mevcuttur. Özellikle, Ernst Zermelo tarafından sağlanan ve günümüzde yalnızca tarihsel bir öneme sahip olan bir yapı, Zermelo sıralı sayıları olarak adlandırılmaktadır. Bu yapıda 0, boş küme olarak tanımlanır ve S(a) = {a} ifadesi kullanılır.

Bu tanım çerçevesinde her bir doğal sayı, bir singleton kümesi olarak ele alınır. Bu nedenle, doğal sayıların temsil etme özelliği doğrudan erişilebilir değildir; yalnızca ordinal özellik (bir dizi içindeki n'inci eleman olma) derhal algılanabilir. Von Neumann yapısının aksine, Zermelo sıralı sayıları, sonsuz sıralı sayılara genişletilemez.

Ayrıca bakınız

(Sayı sistemleri) Karmaşık ${\displaystyle :\;\mathbb {C} }$ Reel ${\displaystyle :\;\mathbb {R} }$ Rasyonel ${\displaystyle :\;\mathbb {Q} }$ Tam sayı ${\displaystyle :\;\mathbb {Z} }$ Doğal ${\displaystyle :\;\mathbb {N} }$ Sıfır: 0 Bir: 1 Asal sayılar Bileşik sayılar Negatif tam sayılar Kesir Devirli ondalık sayı İrrasyonel Cebirsel irrasyonel Aşkın Sanal

Not listesi

1. ^ Carothers (2000, s. 3) "${\displaystyle \mathbb {N} }$ pozitif tam sayılar kümesidir." demektedir. Her iki tanım da gerektiğinde benimsenmektedir ve sıfırın doğal sayılar kümesine dahil edilip edilmemesi konusunda evrensel bir mutabakat bulunmamaktadır.
2. ^ Mendelson (2008): "Bu muazzam sayı sistemleri hiyerarşisi, doğal sayılara dair birkaç temel varsayım üzerinden yalnızca küme teorisi yöntemleri kullanılarak kurulmuştur."
3. ^ Bluman (2010): "Sayılar, matematiğin temel taşını oluşturur."
4. ^ Kish'te keşfedilen bir tablet... M.Ö. 700 civarına tarihlenmekte ve pozisyonel notasyonda boş bir alanı göstermek için üç kancadan faydalanmaktadır. Benzer dönemlere ait diğer tabletler, boş bir alanı işaretlemek için tek bir kancanın kullanıldığını gösterir.
5. ^ Bu kural, Öklid'in Elementleri gibi eserlerde uygulanmaktadır, D. Joyce tarafından hazırlanan Kitap VII'nin web versiyonuna bakınız.
6. ^ Bu İngilizce çeviri Gray tarafından yapılmıştır. Gray, bu Almanca alıntıyı "Weber 1891–1892, 19, Kronecker'in 1886 yılında verdiği bir dersi alıntılayarak" şeklinde kaynak göstermiştir.
7. ^ "Yirminci yüzyılın matematik çalışmalarının önemli bir bölümü, disiplinin mantıksal temellerini ve yapısal özelliklerini detaylı bir şekilde inceleme çabalarına adanmıştır." Eves 1990, s. 606
8. ^ Mac Lane & Birkhoff (1999, s. 15) doğal sayılar içinde sıfırı da dahil eder: 'Sezgisel olarak, tüm doğal sayıların kümesi ${\displaystyle \mathbb {N} ={0,1,2,\ldots }}$ şu şekilde tanımlanabilir: ${\displaystyle \mathbb {N} }$, bir "başlangıç" sayısı 0 içerir; ...'. Bu tanımı, Peano Aksiyomlarının kendi versiyonlarını takip ederek yaparlar.

Kaynakça

1. ^ Banerjee, Reina. Modern School Mathematics Book - 7 (İngilizce). Orient Blackswan. ss. 7-8. ISBN . 
2. ^ ^{a b c} "Standard number sets and intervals" (PDF). ISO 80000-2:2019 (İngilizce). International Organization for Standardization. 19 Mayıs 2020. s. 4. 13 Mart 2023 tarihinde kaynağından . Erişim tarihi: 17 Şubat 2024. 
3. ^ . Merriam-Webster.com (İngilizce). Merriam-Webster. 13 Aralık 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ekim 2014. 
4. ^ ^{a b c} Weisstein, Eric W. "Natural Number" (İngilizce). 29 Haziran 2023 tarihinde kaynağından . Erişim tarihi: 11 Ağustos 2020. 
5. ^ Ganssle, Jack G.; Barr, Michael (2003). "integer". Embedded Systems Dictionary (İngilizce). Taylor & Francis. ss. 138 (integer), 247 (signed integer), & 276 (unsigned integer). ISBN . 29 Mart 2017 tarihinde kaynağından . Erişim tarihi: 28 Mart 2017 – Google Books vasıtasıyla. 
6. ^ Eric W. Weisstein, Counting Number (MathWorld)
7. ^ "Natural Numbers" (İngilizce). 9 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 11 Ağustos 2020. 
8. ^ . İşango kemiği (İngilizce). Brüksel, Belçika: . 4 Mart 2016 tarihinde kaynağından arşivlendi. 
9. ^ . İşango kemiği (İngilizce). Brüksel, Belçika: . 27 Mayıs 2016 tarihinde kaynağından arşivlendi. 
10. ^ (İngilizce). 10 Kasım 2014 tarihinde kaynağından arşivlendi. 
11. ^ Ifrah, Georges (2000). The Universal History of Numbers (İngilizce). Wiley. ISBN . 
12. ^ . MacTutor Matematik Tarihi. 19 Ocak 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ocak 2013. 
13. ^ Mann, Charles C. (2005). 1491: New Revelations of the Americas before Columbus. Knopf. s. 19. ISBN . 14 Mayıs 2015 tarihinde kaynağından . Erişim tarihi: 3 Şubat 2015 – Google Books vasıtasıyla. 
14. ^ Evans, Brian (2014). "Chapter 10. Pre-Columbian Mathematics: The Olmec, Maya, and Inca Civilizations". The Development of Mathematics Throughout the Centuries: A brief history in a cultural context. John Wiley & Sons. ISBN  – Google Books vasıtasıyla. 
15. ^ Deckers, Michael (25 Ağustos 2003). "Cyclus Decemnovennalis Dionysii – Nineteen year cycle of Dionysius". Hbar.phys.msu.ru. 15 Ocak 2019 tarihinde kaynağından . Erişim tarihi: 13 Şubat 2012. 
16. ^ Euclid. "Book VII, definitions 1 and 2". Joyce, D. (Ed.). . Clark University. 
17. ^ Mueller, Ian (2006). Philosophy of mathematics and deductive structure in Euclid's Elements. Mineola, New York: Dover Publications. s. 58. ISBN . OCLC 69792712. 
18. ^ Euclid. "Book VII, definition 22". Joyce, D. (Ed.). . Clark University. A perfect number is that which is equal to the sum of its own parts.  In definition VII.3 a "part" was defined as a number, but here 1 is considered to be a part, so that for example 6 = 1 + 2 + 3 is a perfect number.
19. ^ Kline, Morris (1990) [1972]. Mathematical Thought from Ancient to Modern Times. Oxford University Press. ISBN . 
20. ^ Poincaré, Henri (1905). "On the nature of mathematical reasoning". La Science et l'hypothèse [Science and Hypothesis] (İngilizce). Greenstreet, William John tarafından çevrildi. VI. 
21. ^ (2008). Plato's Ghost: The modernist transformation of mathematics. Princeton University Press. s. 153. ISBN . 29 Mart 2017 tarihinde kaynağından – Google Books vasıtasıyla. 
22. ^ Weber, Heinrich L. (1891–1892). . Jahresbericht der Deutschen Mathematiker-Vereinigung [Annual report of the German Mathematicians Association]. ss. 2:5-23. (The quote is on p. 19). 9 Ağustos 2018 tarihinde kaynağından arşivlendi;  . 20 Ağustos 2017 tarihinde kaynağından arşivlendi. 
23. ^ Eves 1990, Chapter 15
24. ^ Kirby, Laurie; Paris, Jeff (1982). "Accessible Independence Results for Peano Arithmetic". Bulletin of the London Mathematical Society. Wiley. 14 (4): 285-293. doi:10.1112/blms/14.4.285. ISSN 0024-6093. 
25. ^ Bagaria, Joan (2017). Set Theory (Winter 2014 bas.). The Stanford Encyclopedia of Philosophy. 14 Mart 2015 tarihinde kaynağından . Erişim tarihi: 13 Şubat 2015. 
26. ^ Goldrei, Derek (1998). "3". Classic Set Theory: A guided independent study (1. ed., 1. print bas.). Boca Raton, Fla. [u.a.]: Chapman & Hall/CRC. s. 33. ISBN . 
27. ^ Brown, Jim (1978). "In defense of index origin 0". ACM SIGAPL APL Quote Quad. 9 (2): 7. doi:10.1145/586050.586053. 
28. ^ Hui, Roger. "Is index origin 0 a hindrance?". jsoftware.com. 20 Ekim 2015 tarihinde kaynağından . Erişim tarihi: 19 Ocak 2015. 
29. ^ This is common in texts about . See, for example, Carothers (2000, s. 3) or Thomson, Bruckner & Bruckner (2008, s. 2).
30. ^ "Listing of the Mathematical Notations used in the Mathematical Functions Website: Numbers, variables, and functions". functions.wolfram.com. 9 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 27 Temmuz 2020. 
31. ^ Rudin, W. (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. s. 25. ISBN . 
32. ^ Grimaldi, Ralph P. Discrete and Combinatorial Mathematics: An applied introduction (5.5yıl=2004 bas.). Pearson Addison Wesley. ISBN . 
33. ^ {{Kitap kaynağı |soyadı1=Grimaldi |ad1=Ralph P. |başlık=A review of discrete and combinatorial mathematics |tarih=2003 |yayıncı=Addison-Wesley |yer=Boston |isbn=978-0-201-72634-3 |sayfa=133 |basım=5.5
34. ^ Weisstein, Eric W. "Multiplication". mathworld.wolfram.com (İngilizce). 4 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 27 Temmuz 2020. 
35. ^ Fletcher, Harold; Howell, Arnold A. (9 Mayıs 2014). Mathematics with Understanding (İngilizce). Elsevier. s. 116. ISBN . 15 Eylül 2023 tarihinde kaynağından . Erişim tarihi: 21 Şubat 2024. ...the set of natural numbers is closed under addition... set of natural numbers is closed under multiplication 
36. ^ Davisson, Schuyler Colfax (1910). College Algebra (İngilizce). Macmillian Company. s. 2. 15 Eylül 2023 tarihinde kaynağından . Erişim tarihi: 21 Şubat 2024. Addition of natural numbers is associative. 
37. ^ Brandon, Bertha (M.); Brown, Kenneth E.; Gundlach, Bernard H.; Cooke, Ralph J. (1962). Laidlaw mathematics series (İngilizce). 8. Laidlaw Bros. s. 25. 15 Eylül 2023 tarihinde kaynağından . Erişim tarihi: 21 Şubat 2024. 
38. ^ Mints, G.E. ((Ed.)). "Peano axioms". Encyclopedia of Mathematics. , in cooperation with the . 13 Ekim 2014 tarihinde kaynağından . Erişim tarihi: 8 Ekim 2014. 
39. ^ von Neumann (1923)
40. ^ Levy (1979)

Bibliografya

• Bluman, Allan (2010). Pre-Algebra DeMYSTiFieD (Second bas.). McGraw-Hill Professional. ISBN  – Google Books vasıtasıyla. 
• Carothers, N.L. (2000). Real Analysis. Cambridge University Press. ISBN  – Google Books vasıtasıyla. 
• Clapham, Christopher; Nicholson, James (2014). The Concise Oxford Dictionary of Mathematics (Fifth bas.). Oxford University Press. ISBN  – Google Books vasıtasıyla. 
• Dedekind, Richard (1963) [1901]. Essays on the Theory of Numbers. Beman, Wooster Woodruff tarafından çevrildi (reprint bas.). Dover Books. ISBN  – Archive.org vasıtasıyla. 
  • Dedekind, Richard (1901). Essays on the Theory of Numbers. Beman, Wooster Woodruff tarafından çevrildi. Chicago, IL: Open Court Publishing Company. Erişim tarihi: 13 Ağustos 2020 – Project Gutenberg vasıtasıyla. 
  • Dedekind, Richard (2007) [1901]. Essays on the Theory of Numbers. Kessinger Publishing, LLC. ISBN . 
• (1990). (6.6başlık=An Introduction to the History of Mathematics bas.). Thomson. ISBN  https://books.google.com/books?id=PXvwAAAAMAAJ – Google Books vasıtasıyla.  Eksik ya da boş |başlık= ()
• (1960). Naive Set Theory. Springer Science & Business Media. ISBN  – Google Books vasıtasıyla. 
• Hamilton, A.G. (1988). Logic for Mathematicians (Revised bas.). Cambridge University Press. ISBN  – Google Books vasıtasıyla. 
• ; James, Glenn (1992). Mathematics Dictionary (Fifth bas.). Chapman & Hall. ISBN  – Google Books vasıtasıyla. 
• Landau, Edmund (1966). Foundations of Analysis (Third bas.). Chelsea Publishing. ISBN  – Google Books vasıtasıyla. 
• (1979). Basic Set Theory. Springer-Verlag Berlin Heidelberg. ISBN . 
• ; Birkhoff, Garrett (1999). (3.3başlık=Algebra bas.). American Mathematical Society. ISBN  https://books.google.com/books?id=L6FENd8GHIUC&q=%22the+natural+numbers%22&pg=PA15 – Google Books vasıtasıyla.  Eksik ya da boş |başlık= ()
• (2008) [1973]. Number Systems and the Foundations of Analysis. Dover Publications. ISBN  – Google Books vasıtasıyla. 
• Morash, Ronald P. (1991). Bridge to Abstract Mathematics: Mathematical proof and structures (Second bas.). Mcgraw-Hill College. ISBN  – Google Books vasıtasıyla. 
• Musser, Gary L.; Peterson, Blake E.; Burger, William F. (2013). (10.10başlık=Mathematics for Elementary Teachers: A contemporary approach bas.). . ISBN  https://books.google.com/books?id=b3dbAgAAQBAJ – Google Books vasıtasıyla.  Eksik ya da boş |başlık= ()
• Szczepanski, Amy F.; Kositsky, Andrew P. (2008). The Complete Idiot's Guide to Pre-algebra. Penguin Group. ISBN  – Google Books vasıtasıyla. 
• Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008). Elementary Real Analysis (Second bas.). ClassicalRealAnalysis.com. ISBN  – Google Books vasıtasıyla. 
• von Neumann, John (1923). [On the Introduction of the Transfinite Numbers]. Acta Litterarum AC Scientiarum Ragiae Universitatis Hungaricae Francisco-Josephinae, Sectio Scientiarum Mathematicarum. 1: 199-208. 18 Aralık 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 15 Eylül 2013. 
• von Neumann, John (January 2002) [1923]. "On the introduction of transfinite numbers". van Heijenoort, Jean (Ed.). (3.3başlık=From Frege to Gödel: A source book in mathematical logic, 1879–1931 bas.). Harvard University Press. ss. 346-354. ISBN .  Eksik ya da boş |başlık= () – English translation of von Neumann 1923.