Fizikte, káÝsmen kuantum (nicem) mekaniáinde, atomun vektûÑr modeli atom modelinin aûÏáÝsal momentum (devinim) cinsinden tanáÝmáÝdáÝr. Bu, birden ûÏok elektronlu atomlaráÝn Rutherford-Bohr-Sommerfeld atom modelinin bir geniéletmesi olarak kabul edilebilir.
Girié

Bu model atomda, elektronlaráÝn aûÏáÝsal momentumunun tanáÝmáÝ iûÏin elveriélidir. AûÏáÝsal momentum her zaman L orbitali (yûÑrû¥ngesi),S sipini (fáÝráÝláÝ) ve toplam J arasáÝnda paylaétáÝráÝláÝr:
Bu verilen formû¥l kuantum mekaniáinde, aûÏáÝsal momentum kuantize edilir (nicemlenir) ve burada her vektûÑrû¥n bileékesi arasáÝnda kesin olmayan bir iliéki vardáÝr ki bu durumu matematiksel arka planáÝn oldukûÏa kompleks olmasáÝna raámen oldukûÏa basitleétirir. Geometriksel olarak bu ayráÝk dik dairesel konilerin dairesel tabanlaráÝ olmadan bû¥tû¥n eksenlerin tek bir eksen etrafáÝnda sáÝralanmasáÝdáÝr. Eáer 3 boyutlu kartezyen koordinatlaráÝnda ûÏaláÝéáÝláÝyorsa bu eksen z ekseni olur. á¯zleyen konular bu hususun arka planáÝnáÝ oluéturmaktadáÝr.
AûÏáÝsal Momentumun Matematiksel Arka PlanáÝ

Komû¥tatûÑr (ûndeleyici), L, S ve J'nin her biri iûÏin, bir anláÝk zamanda herhangi bir aûÏáÝsal momentumun (devinim) sadece bir bileékesinin hesaplanabilir olduáunu belirtir. Komû¥tatûÑrû¥n iki aûÏáÝsal momentum iélemcisi sáÝfáÝr olamaz. á¯zleyen bilgiler vektûÑr modelin inéasáÝnda baálantáÝláÝ matematiksel olgularáÝn bir ûÑzetidir.
Deáiétirim iliékileri aéaááÝdaki gibidir ( kullanáÝldáÝááÝnda):
Bu denklemde,
- L = (L1, L2, L3), S = (S1, S2, S3) ve J = (J1, J2, J3) (BunlaráÝn kartezyen koordinatta tekabû¥l ettikleri bileékeler L = (Lx, Ly, Lz), S = (Sx, Sy, Sz) ve J = (Jx, Jy, Jz) ),
- a, b, c ã {1,2,3} aûÏáÝsal momentumun bileékelerinin indeksleridir.
- öçabc 3 boyutta 3-indeksli (gericisidir).
Fakat L, S ve J'nin bû¥yû¥klû¥kleri aynáÝ anda ûÑlûÏû¥lebilir ûÏû¥nkû¥ aûÏáÝsal momentumun iélemcisinin karesinin herhangi bir bileéke ile deáiétirimi sáÝfáÝrdáÝr. DolayáÝsáÝyla 

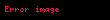


Bu bû¥yû¥klû¥kler aéaááÝdaki denklemleri iélemci ve vektûÑr bileékesi cinsinden yazáÝldáÝááÝnda da saálamaktadáÝr.
ve kuantum (nicem) numaralaráÝ;
Bu denklemde,
, aûÏáÝsal nicem sayáÝsáÝ
- s, parûÏacáÝááÝn tipine gûÑre
- j,
bunlar ayráÝ ayráÝ deáerler aldáÝááÝnda,
Bu matematiksel yargáÝlar belirli kuantum numaralaráÝnáÝn yerini tutan bû¥tû¥n olasáÝ aûÏáÝsal momentum sû¥reci tanáÝmlamaktadáÝr.
- Bir doárultu sabit, diáer iki doárultu ise deáiékendir.
- VektûÑrlerin bû¥yû¥kleri sabit olmak zorundadáÝr. DolayáÝsáÝyla vektûÑrlerin orta dereceli her bir bileékesi bir ûÏember tarafáÝndan kapaláÝ olmak zorundadáÝr. éûÑyle ki ûÑlûÏû¥lebilir ve ûÑlûÏû¥lemez bileékeler olasáÝ bû¥tû¥n orta dereceli bileékelerin bû¥yû¥klû¥klerini doáru bir éekilde inéa etmeyi mû¥mkû¥n káÝlar.
Geometrik sonuûÏ bir vektûÑr konisidir ve bu vektûÑr koninin tepe noktasáÝndan baélayáÝp koninin ûÏevresine kadar ulaémaktadáÝr. Bu toplantáÝ aûÏáÝsal momentumun ûÑlûÏû¥lebilir bileékesini bulmak iûÏin z eksenini kulannmaktadáÝr. Bu eksen dû¥zleme dik olan, koninin ûÏevresel tabanáÝ tarafáÝndan tanáÝmlanmáÝé koninin tepesinden dû¥zleme doáru yûÑnelmié bir eksendir. FarkláÝ kuantum numaralaráÝ iûÏin koniler farkláÝláÝk gûÑsterir. DolayáÝsáÝyla buradaki aûÏáÝsal momentum durumunun ayráÝk numaralaráÝ 


Koni sayáÝlaráÝ durumlaráÝn ûÏarpáÝlmasáÝna eéittir, 
Bohr model
Bu durum Bohr modelinin bir uzantáÝsáÝ olarak da kabul edilebilir ûÏû¥nkû¥ Niels Bohr'da aûÏáÝsal momentumun kuantize (nicemlenmié) olduáunu ûÑnermiétir. Bohr'a gûÑre bu kuantizasyon aéaááÝdaki formû¥le gûÑre gerûÏekleéir.
bu formû¥ldeki m, Hidrojen atomu iûÏin doáru sonuûÏlar sunan bir tam sayáÝdáÝr. Bohr modeli ûÏok elektronlu atomlara uygulanamamasáÝna raámen bu yûÑntem, atomun vektûÑr modelinden ûÑnce gelen, atoma uygulan ilk baéaráÝláÝ aûÏáÝsal momentum kuantizasyonudur.
AûÏáÝsal Momentumun (Devinimin) Eklenmesi
Hidrojen gibi bir elektronlu atomlarda yûÑrû¥ngelerdeki elektronlar iûÏin sadece bir grup koni vardáÝr. ûok elektronlu atomlar iûÏin ise artan elektron sayáÝsáÝndan dolayáÝ birûÏok hal sûÑzkonsudur.
Atomdaki bû¥tû¥n elektonlaráÝn aûÏáÝsal momentumu vektûÑrel olarak eklenir. BirûÏok atomik iélem sû¥reci, nû¥kleer veya kimyasal fark etmeksizin koméu ûÏekirdek tanecikleri ve elektronlar yû¥zû¥nden -radyoaktif áÝéáÝmanáÝn (áÝéáÝnsaûÏar bozunum) tahmini iélem sû¥reci hariûÏ -spin(fáÝráÝl)- paylaéáÝmáÝ ve aûÏáÝsal momentum baálaéáÝmáÝ ile aûÏáÝklanabilir. Bu konuda "baálaéáÝm" terimi aûÏáÝsal momentumun vektûÑr û¥stdû¥éû¥mleri anlamáÝna gelmektedir. Bu da bû¥yû¥klû¥klerin ve yûÑnlerin eklendiái anlamáÝna gelir.
ûok elektronlu atomlarda, iki aûÏáÝsal momentumun vektûÑr toplamáÝ éu éekilde olur;
eáer z bileékesini gûÑre aláÝcak olursak;
burada
ve de bileékelerin bû¥yû¥klû¥kleri
olur. Bu durum aéaááÝdaki koéulda geûÏerlidir;
Bu iélem sû¥reci toplam aûÏáÝsal momentum bulunana kadar, û¥ûÏû¥ncû¥ veya dûÑrdû¥ncû¥ bir elektron iûÏin tekrar edilebilir.
LS BaálaéáÝmáÝ

Bû¥tû¥n aûÏáÝsal momentumlaráÝn birbirine eklenmesi oldukûÏa zahmetli bir konudur. z-ekseni etrafáÝnda bulunan bû¥tû¥n devinik momentum konileri hesaba katáÝlmak zorundadáÝr ûÏû¥nkû¥ sonuûÏda elde edilecek momentum kesin deáildir. Bu durum L-S baálaéáÝmáÝndaki, H.N. Russell ve F.A. Saunders tarafáÝndan adlandáÝráÝlan Russell-Suanders baálaéáÝmáÝ gibi bir takáÝm yakáÝnlaétáÝrmalarla daha kolay bir hale getirilebilir.
KaynakûÏa
Konuyla ilgili yayáÝnlar
- Atomic Many-Body Theory, I. Lindgren, J. Morrison, Springer-Verlag Series in: Chemical Physics No13, 1982, ISBN, Graduate level monograph on many body theory in the context of angular momentum, with much emphasis on graphical representation and methods.
- Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill, 2005,
wikipedia, wiki, viki, vikipedia, oku, kitap, kû¥tû¥phane, kû¥tû¥bhane, ara, ara bul, bul, heréey, ne arasanáÝz burada,hikayeler, makale, kitaplar, ûÑáren, wiki, bilgi, tarih, yukle, izle, telefon iûÏin, turk, tû¥rk, tû¥rkûÏe, turkce, nasáÝl yapáÝláÝr, ne demek, nasáÝl, yapmak, yapáÝláÝr, indir, û¥cretsiz, û¥cretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mû¥zik, éarkáÝ, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte kismen kuantum nicem mekaniginde atomun vektor modeli atom modelinin acisal momentum devinim cinsinden tanimidir Bu birden cok elektronlu atomlarin Rutherford Bohr Sommerfeld atom modelinin bir genisletmesi olarak kabul edilebilir GirisYorungenin acisal momentumunun vektor modelinin cizimi Bu model atomda elektronlarin acisal momentumunun tanimi icin elverislidir Acisal momentum her zaman Lorbitali yorungesi S sipini firili ve toplam Jarasinda paylastirilir J L S displaystyle mathbf J mathbf L mathbf S Bu verilen formul kuantum mekaniginde acisal momentum kuantize edilir nicemlenir ve burada her vektorun bileskesi arasinda kesin olmayan bir iliski vardir ki bu durumu matematiksel arka planin oldukca kompleks olmasina ragmen oldukca basitlestirir Geometriksel olarak bu ayrik dik dairesel konilerin dairesel tabanlari olmadan butun eksenlerin tek bir eksen etrafinda siralanmasidir Eger 3 boyutlu kartezyen koordinatlarinda calisiliyorsa bu eksen z ekseni olur Izleyen konular bu hususun arka planini olusturmaktadir Acisal Momentumun Matematiksel Arka Plani Spin acisal momentumunun konileri Burada 1 2 parcacigi icin olan bir spin gosterilmistir Komutator Ondeleyici L S ve J nin her biri icin bir anlik zamanda herhangi bir acisal momentumun devinim sadece bir bileskesinin hesaplanabilir oldugunu belirtir Komutatorun iki acisal momentum islemcisi sifir olamaz Izleyen bilgiler vektor modelin insasinda baglantili matematiksel olgularin bir ozetidir Degistirim iliskileri asagidaki gibidir kullanildiginda L a L b iãeabcL c S a S b iãeabcS c displaystyle begin aligned amp hat L a hat L b i hbar varepsilon abc hat L c amp hat S a hat S b i hbar varepsilon abc hat S c end aligned Bu denklemde L L1 L2 L3 S S1 S2 S3 ve J J1 J2 J3 Bunlarin kartezyen koordinatta tekabul ettikleri bileskeler L Lx Ly Lz S Sx Sy Sz ve J Jx Jy Jz a b c 1 2 3 acisal momentumun bileskelerinin indeksleridir eabc 3 boyutta 3 indeksli gericisidir Fakat L S ve J nin buyuklukleri ayni anda olculebilir cunku acisal momentumun islemcisinin karesinin herhangi bir bileske ile degistirimi sifirdir Dolayisiyla L a displaystyle hat L a ile L 2 displaystyle hat L 2 nin S a displaystyle hat S a ile S 2 displaystyle hat S 2 nin ve J a displaystyle hat J a ile J 2 displaystyle hat J 2 nin ayni anda olcumu asagidaki esitligi saglamaktadir L a L 2 0 S a S 2 0 J a J 2 0 displaystyle begin aligned amp hat L a hat L 2 0 amp hat S a hat S 2 0 amp hat J a hat J 2 0 end aligned Bu buyuklukler asagidaki denklemleri islemci ve vektor bileskesi cinsinden yazildiginda da saglamaktadir L 2 L x2 L y2 L z2 L L L2 Lx2 Ly2 Lz2 S 2 S x2 S y2 S z2 S S S2 Sx2 Sy2 Sz2 J 2 J x2 J y2 J z2 J J J2 Jx2 Jy2 Jz2 displaystyle begin aligned amp hat L 2 hat L x 2 hat L y 2 hat L z 2 rightleftharpoons mathbf L cdot mathbf L L 2 L x 2 L y 2 L z 2 amp hat S 2 hat S x 2 hat S y 2 hat S z 2 rightleftharpoons mathbf S cdot mathbf S S 2 S x 2 S y 2 S z 2 amp hat J 2 hat J x 2 hat J y 2 hat J z 2 rightleftharpoons mathbf J cdot mathbf J J 2 J x 2 J y 2 J z 2 end aligned ve kuantum nicem numaralari L ãã ã 1 Lz mãã S ãs s 1 Sz msã J ãj j 1 Jz mjã displaystyle begin aligned amp mathbf L hbar sqrt ell ell 1 quad L z m ell hbar amp mathbf S hbar sqrt s s 1 quad S z m s hbar amp mathbf J hbar sqrt j j 1 quad J z m j hbar end aligned Bu denklemde ã displaystyle scriptstyle ell acisal nicem sayisi s parcacigin tipine gore j bunlar ayri ayri degerler aldiginda mã ã ã 1 ã 1 ã ã 0 1 n 1 ms s s 1 s 1 s mj j j 1 j 1 j mj mã ms j ã s displaystyle begin aligned amp m ell in ell ell 1 cdots ell 1 ell quad ell in 0 1 cdots n 1 amp m s in s s 1 cdots s 1 s amp m j in j j 1 cdots j 1 j amp m j m ell m s quad j ell s end aligned Bu matematiksel yargilar belirli kuantum numaralarinin yerini tutan butun olasi acisal momentum sureci tanimlamaktadir Bir dogrultu sabit diger iki dogrultu ise degiskendir Vektorlerin buyukleri sabit olmak zorundadir Dolayisiyla vektorlerin orta dereceli her bir bileskesi bir cember tarafindan kapali olmak zorundadir Soyle ki olculebilir ve olculemez bileskeler olasi butun orta dereceli bileskelerin buyukluklerini dogru bir sekilde insa etmeyi mumkun kilar Geometrik sonuc bir vektor konisidir ve bu vektor koninin tepe noktasindan baslayip koninin cevresine kadar ulasmaktadir Bu toplanti acisal momentumun olculebilir bileskesini bulmak icin z eksenini kulannmaktadir Bu eksen duzleme dik olan koninin cevresel tabani tarafindan tanimlanmis koninin tepesinden duzleme dogru yonelmis bir eksendir Farkli kuantum numaralari icin koniler farklilik gosterir Dolayisiyla buradaki acisal momentum durumunun ayrik numaralari ã displaystyle scriptstyle ell s ve jtarafindan belirlenebilir Bir onceki koninin bir parcasi olan vektor kurulumunu kullanarak her bir durum bir koni yerine kullanilabilir Bu durumda artan ã displaystyle scriptstyle ell s ve j ve azalan ã displaystyle scriptstyle ell s ve j gt negatif eksi kuantum sayilari x y duzlemindeki konilere karsilik gelir Uc durumdan biri sifira esit olan bir kuantum numarasi icin acikca bir koniye karsilik gelmemektedir Bu durum sadece x y duzlemindeki bir cember icin gecerlidir Koni sayilari durumlarin carpilmasina esittir 2ã 1 displaystyle scriptstyle 2 ell 1 Bohr model Bu durum Bohr modelinin bir uzantisi olarak da kabul edilebilir cunku Niels Bohr da acisal momentumun kuantize nicemlenmis oldugunu onermistir Bohr a gore bu kuantizasyon asagidaki formule gore gerceklesir L mã displaystyle L m hbar bu formuldeki m Hidrojen atomu icin dogru sonuclar sunan bir tam sayidir Bohr modeli cok elektronlu atomlara uygulanamamasina ragmen bu yontem atomun vektor modelinden once gelen atoma uygulan ilk basarili acisal momentum kuantizasyonudur Acisal Momentumun Devinimin EklenmesiHidrojen gibi bir elektronlu atomlarda yorungelerdeki elektronlar icin sadece bir grup koni vardir Cok elektronlu atomlar icin ise artan elektron sayisindan dolayi bircok hal sozkonsudur Atomdaki butun elektonlarin acisal momentumu vektorel olarak eklenir Bircok atomik islem sureci nukleer veya kimyasal fark etmeksizin komsu cekirdek tanecikleri ve elektronlar yuzunden radyoaktif isimanin isinsacar bozunum tahmini islem sureci haric spin firil paylasimi ve acisal momentum baglasimi ile aciklanabilir Bu konuda baglasim terimi acisal momentumun vektor ustdusumleri anlamina gelmektedir Bu da buyukluklerin ve yonlerin eklendigi anlamina gelir Cok elektronlu atomlarda iki acisal momentumun vektor toplami su sekilde olur J J1 J2 displaystyle mathbf J mathbf J 1 mathbf J 2 eger z bileskesini gore alicak olursak Jz J1z J2z displaystyle J z J 1z J 2z burada Jz mjãJ1z mj1ãJ2z mj2ã displaystyle begin aligned amp mathbf J z m j hbar amp mathbf J 1z m j 1 hbar amp mathbf J 2z m j 2 hbar end aligned ve de bileskelerin buyuklukleri J ãj j 1 J1 ãj1 j1 1 J2 ãj2 j2 1 displaystyle begin aligned amp mathbf J hbar sqrt j j 1 amp mathbf J 1 hbar sqrt j 1 j 1 1 amp mathbf J 2 hbar sqrt j 2 j 2 1 end aligned olur Bu durum asagidaki kosulda gecerlidir j j1 j2 j1 j2 1 j1 j2 1 j1 j2 displaystyle j in j 1 j 2 j 1 j 2 1 cdots j 1 j 2 1 j 1 j 2 Bu islem sureci toplam acisal momentum bulunana kadar ucuncu veya dorduncu bir elektron icin tekrar edilebilir LS BaglasimiL S baglasimi tasviri Toplam acisal momentum Jmor renge yorunge L mavi renge ve spin firil S yesil renge boyanmistir Butun acisal momentumlarin birbirine eklenmesi oldukca zahmetli bir konudur z ekseni etrafinda bulunan butun devinik momentum konileri hesaba katilmak zorundadir cunku sonucda elde edilecek momentum kesin degildir Bu durum L S baglasimindaki H N Russell ve F A Saunders tarafindan adlandirilan Russell Suanders baglasimi gibi bir takim yakinlastirmalarla daha kolay bir hale getirilebilir Kaynakca Quanta A handbook of concepts P W Atkins Oxford University Press 1974 ISBN 0 19 855493 1 Physical chemistry P W Atkins Oxford University Press 1978 ISBN 0 19 855148 7 H N Russell and F A Saunders New Regularities in the Spectra of the Alkaline Earths Astrophysical Journal vol 61 p 38 1925 Konuyla ilgili yayinlarAtomic Many Body Theory I Lindgren J Morrison Springer Verlag Series in Chemical Physics No13 1982 ISBN Graduate level monograph on many body theory in the context of angular momentum with much emphasis on graphical representation and methods Quantum Mechanics Demystified D McMahon Mc Graw Hill 2005 ISBN 0 07 145546 9
 Azèrbaycanca
Azèrbaycanca ÅÅçţůîîîŤî
ÅÅçţůîîîŤî Dansk
Dansk Deutsch
Deutsch EspaûÝola
EspaûÝola FranûÏais
FranûÏais Indonesia
Indonesia Italiana
Italiana ÌË̘҈
ÌË̘҈ ØůÅñůØ
ØůÅñůØ Lietuvos
Lietuvos Nederlands
Nederlands Portuguûˆs
Portuguûˆs Å îîſ
Å îîſ ÁñÁñÁÑÁñÁѧ
ÁñÁñÁÑÁñÁѧ Á¿Á¡Á¡Á¿Á¡Á¡Â
Á¿Á¡Á¡Á¿Á¡Á¡Â Tû¥rkûÏe
Tû¥rkûÏe ÅÈŤîůîŧîîŤů
ÅÈŤîůîŧîîŤů ð¡ÙÍð¤¤
ð¡ÙÍð¤¤ United State
United State Afrikaans
Afrikaans