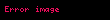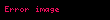Matematikte, bir açıkorur gönderim açıları koruyan bir fonksiyondur. En genel haliyle, fonksiyon karmaşık düzlemdeki bölgeler arasındadır.

Daha formel olarak, bir
gönderimi bir noktasından geçen eğrilerin arasındaki yönlü açıları ve açıların yönlerini koruyorsa, bu gönderime noktasında açıkorur adı verilir. Açıkorur gönderimler hem açıları hem de sonsuz küçüklükteki figürlerin şekillerini korurlar; ancak boyutlarını korumayabilir de.
Açıkorur özelliği bir (koordinat dönüşümünün) Jakoben türevi matrisiyle de açıklanabilir. Eğer dönüşümün Jakoben matrisi her yerde bir skaler ile çarpımıysa, o zaman dönüşüm açıkorurdur.
Açıkorur gönderimler daha yüksek boyutlu Öklid uzaylarındaki veya daha genel bir şekilde bir üzerindeki bölgeler arasında da tanımlanabilir.
Karmaşık analiz
Açıkorur gönderimlerin önemli bir ailesi karmaşık analizden gelmektedir. Eğer U, karmaşık düzlem 
fonksiyonu ancak ve ancak holomorf ise ve türevi U üzerindeki her yerde sıfırdan farklıysa, açıkorurdur. Eğer f tersholomorf ise (yani, holomorf bir fonksiyona ), açıları yine korur ancak bu sefer yönleri tersine çevirir.
Karmaşık analizin çok derin sonuçlarından biri olan Riemann gönderim teoremi 

Genişletilmiş karmaşık düzlemin (ki bir küreye ) kendi üzerine bir gönderimi ancak ve ancak ise açıkorurdur. Yine, için, açılar korunur ancak yönler terine çevrilir.
Sonuncunun bir örneği ise birim çembere göre "çember tersinmesi"ne karşılıık gelen eşleniğin tersini almaktır. Bu ayrıca açıyı aynı tutan, yarıçapsal koordinatın tersini almak olarak da açıklanabilir.
Riemann geometrisi
Riemann geometrisinde, 




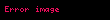

İki Riemann manifoldu arasındaki ise, geri çekilen metrik orijinal metriğe açıkorur olarak denk ise açıkorur gönderim denilir.
Pürüzsüz bir manifold üzerinde aynı zamanda açıkorur olarak denk olan sınıfı cinsinden bir açıkorur yapı da tanımlanabilir.
Örneğin, eklenmiş bir düzleme kürenin açıkorur bir gönderimdir.
Daha yüksek boyutlu Öklid uzayı
Boyutu 2'den fazla olan herhangi bir Öklid uzayının üzerindeki açıkorur bir gönderim 3 çeşit dönüşüm tarafından oluşturulabilir: , ve özel bir açıkorur dönüşüm. (Bir "özel açıkorur dönüşüm" yansıma ve bir bileşkesidir.) Bu yüzden, açıkorur dönüşümlerin boyutu 2'den fazla olan uzaylardaki grubu geniş bir açıkorur dönüşüm grubu sağladığı düzlemdeki durumdan daha sınırlıdır.
Kullanımları
Bir fonksiyon belli bir uzayda harmonikse (yani Laplace denklemi 
Açıkorur dönüşümlerin için önemi ise tarafından 1910'da açığa çıkarılmıştır.
Açıkorur gönderimler mühendislik ve fizikteki karmaşık değişkenli fonksiyonlar cinsinden ifade edilebilen ancak uygunsuz geometriler sergileyen problemlerin çözümü için çok değerlidir. Uygun bir gönderim seçilerek, bir analist uygunsuz bir geometriyi çok daha uygun bir geometriye dönüştürebilir. Mesela, belli bir açıyla ayrılmış iki iletken levhanın köşesinin yakınında konuşlanmış bir nokta yükünden kaynaklanan bir elektrik alanı 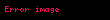

Bu problem kendi başına kapalı bir formda çözülmek için bile çok hantaldır. Bununla birlikte, basit bir açıkorur gönderimle, uygunsuz olan açı pi radyan olan bir açıya gönderilir ki bu da iki levhanın köşesinin diz bir doğruya dönüştürüldüğü anlamına gelir. Bu yeni bölgede, problemin çözülmesi oldukça kolaydır. Çözüm 
Kartografide, harita izdüşümleri adı verilenler ise yine açıkorurdurlar.
Ayrıca bakınız
Kaynakça
- Ahlfors, Lars V. (1973), Conformal invariants: topics in geometric function theory, New York: McGraw-Hill Book Co.
- E.P. Dolzhenko (2001), "Conformal mapping", Hazewinkel, Michiel (Ed.), Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- (1987), Real and complex analysis (3. bas.), New York: McGraw-Hill Book Co., ISBN , MR924157
- Eric W. Weisstein, Açıkorur Gönderim (MathWorld)
Dış bağlantılar
- John H. Mathews. . 29 Eylül 2013 tarihinde kaynağından arşivlendi.
- . 8 Şubat 2016 tarihinde kaynağından arşivlendi.
- . 12 Ekim 2007 tarihinde kaynağından arşivlendi.
- Michael Trott. . . 21 Haziran 2012 tarihinde kaynağından arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir acikorur gonderim acilari koruyan bir fonksiyondur En genel haliyle fonksiyon karmasik duzlemdeki bolgeler arasindadir Dikdortgen bir izgara yukarida ve acikorur bir f gonderimi altindaki goruntusu asagida f nin 90 aciyla kesisen dogru ciftlerini yine 90 aciyla kesisen dogru acilarina gonderdigi goruluyor Daha formel olarak bir w f z displaystyle w f z gonderimi bir z0 displaystyle z 0 noktasindan gecen egrilerin arasindaki yonlu acilari ve acilarin yonlerini koruyorsa bu gonderime z0 displaystyle z 0 noktasinda acikorur adi verilir Acikorur gonderimler hem acilari hem de sonsuz kucuklukteki figurlerin sekillerini korurlar ancak boyutlarini korumayabilir de Acikorur ozelligi bir koordinat donusumunun Jakoben turevi matrisiyle de aciklanabilir Eger donusumun Jakoben matrisi her yerde bir skaler ile carpimiysa o zaman donusum acikorurdur Acikorur gonderimler daha yuksek boyutlu Oklid uzaylarindaki veya daha genel bir sekilde bir uzerindeki bolgeler arasinda da tanimlanabilir Karmasik analizAcikorur gonderimlerin onemli bir ailesi karmasik analizden gelmektedir Eger U karmasik duzlem C displaystyle scriptstyle mathbb C nin acik bir altkumesiyse o zaman f U C displaystyle f U rightarrow scriptstyle mathbb C fonksiyonu ancak ve ancak holomorf ise ve turevi U uzerindeki her yerde sifirdan farkliysa acikorurdur Eger f tersholomorf ise yani holomorf bir fonksiyona acilari yine korur ancak bu sefer yonleri tersine cevirir Karmasik analizin cok derin sonuclarindan biri olan Riemann gonderim teoremi C displaystyle scriptstyle mathbb C nin bos olmayan acik basit baglantili bir ozalt kumesiyle C displaystyle scriptstyle mathbb C deki acik birim disk arasinda birebir ve orten bir acikorur gonderimin varoldugunu soyler Genisletilmis karmasik duzlemin ki bir kureye kendi uzerine bir gonderimi ancak ve ancak ise acikorurdur Yine icin acilar korunur ancak yonler terine cevrilir Sonuncunun bir ornegi ise birim cembere gore cember tersinmesi ne karsiliik gelen eslenigin tersini almaktir Bu ayrica aciyi ayni tutan yaricapsal koordinatin tersini almak olarak da aciklanabilir Riemann geometrisiRiemann geometrisinde M displaystyle M puruzsuz manifoldunun uzerindeki g displaystyle g ve h displaystyle h M displaystyle M uzerindeki pozitif bir u displaystyle u fonksiyonu icin g uh displaystyle g uh esitligi varsa acikorur olarak denk denilir u displaystyle u fonksiyonuna ise acikorur carpan adi verilir Iki Riemann manifoldu arasindaki ise geri cekilen metrik orijinal metrige acikorur olarak denk ise acikorur gonderim denilir Puruzsuz bir manifold uzerinde ayni zamanda acikorur olarak denk olan sinifi cinsinden bir acikorur yapi da tanimlanabilir Ornegin eklenmis bir duzleme kurenin acikorur bir gonderimdir Daha yuksek boyutlu Oklid uzayiBoyutu 2 den fazla olan herhangi bir Oklid uzayinin uzerindeki acikorur bir gonderim 3 cesit donusum tarafindan olusturulabilir ve ozel bir acikorur donusum Bir ozel acikorur donusum yansima ve bir bileskesidir Bu yuzden acikorur donusumlerin boyutu 2 den fazla olan uzaylardaki grubu genis bir acikorur donusum grubu sagladigi duzlemdeki durumdan daha sinirlidir KullanimlariBir fonksiyon belli bir uzayda harmonikse yani Laplace denklemi 2f 0 displaystyle nabla 2 f 0 i sagliyorsa ve acikorur gonderimle baska bir uzaya donusturuluyorsa donusum de harmoniktir Bu nedenle bir tarafindan tanimlanmis herhangi bir fonksiyon acikorur bir gonderim tarafindan da donusturulebilir ve hala bir potansiyel tarafindan hukmedilir durumda kalir Fizikteki bir potansiyel tarafindan tanimlanmis denklemler ornekleri elektromanyetik alani icerir ve akiskanlar dinamiginde sabit yogunluk sifir akiskanlik ve varsayan akiskan akimina bir yaklasim olan icerir Acikorur gonderimin akiskan dinamigi uygulamasindan birisi de Acikorur donusumlerin icin onemi ise tarafindan 1910 da aciga cikarilmistir Acikorur gonderimler muhendislik ve fizikteki karmasik degiskenli fonksiyonlar cinsinden ifade edilebilen ancak uygunsuz geometriler sergileyen problemlerin cozumu icin cok degerlidir Uygun bir gonderim secilerek bir analist uygunsuz bir geometriyi cok daha uygun bir geometriye donusturebilir Mesela belli bir aciyla ayrilmis iki iletken levhanin kosesinin yakininda konuslanmis bir nokta yukunden kaynaklanan bir elektrik alani E z displaystyle E z hesaplanmak istenebilir burada z displaystyle z noktanin 2 uzaydaki karmasik koordinatidir Bu problem kendi basina kapali bir formda cozulmek icin bile cok hantaldir Bununla birlikte basit bir acikorur gonderimle uygunsuz olan aci pi radyan olan bir aciya gonderilir ki bu da iki levhanin kosesinin diz bir dogruya donusturuldugu anlamina gelir Bu yeni bolgede problemin cozulmesi oldukca kolaydir Cozum E w displaystyle E w bu bolgede elde edilir ve orijinal bolgesine geri gonderilir Bu uygulamada acikorur gonderimlerin acilari korudugu gercegine celiski yoktur cunku acilari koruma bolgelerin ici icin gecerlidir sinirlar icin degil Kartografide harita izdusumleri adi verilenler ise yine acikorurdurlar Ayrica bakinizKaynakcaAhlfors Lars V 1973 Conformal invariants topics in geometric function theory New York McGraw Hill Book Co E P Dolzhenko 2001 Conformal mapping Hazewinkel Michiel Ed Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 1987 Real and complex analysis 3 bas New York McGraw Hill Book Co ISBN 978 0 07 054234 1 MR924157 Eric W Weisstein Acikorur Gonderim MathWorld Dis baglantilarJohn H Mathews 29 Eylul 2013 tarihinde kaynagindan arsivlendi 8 Subat 2016 tarihinde kaynagindan arsivlendi 12 Ekim 2007 tarihinde kaynagindan arsivlendi Michael Trott 21 Haziran 2012 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State