Öklid geometrisinde, Batlamyus teoremi, bir (köşeleri ortak bir daire üzerinde yer alan bir dörtgen) dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un (Claudius Ptolemaeus) adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.

Kirişler dörtgenin köşeleri sırayla , , ve ise, teorem şunu belirtir:
Burada dikey çizgiler (| |) ile gösterim, adlandırılmış köşeler arasındaki çizgi parçalarının uzunluklarını belirtmektedir. Geometri bağlamında, yukarıdaki eşitlik genellikle basitçe şöyle yazılır:
Bu ilişki sözlü olarak şu şekilde ifade edilebilir:
- Eğer bir dörtgen bir dairenin içine çizilebiliyorsa, köşegenlerinin uzunluklarının çarpımı, karşıt kenarların çiftlerinin uzunluklarının çarpımlarının toplamına eşittir.
Dahası, Batlamyus teoreminin tersi de doğrudur:
- Bir dörtgende, karşıt iki kenar çiftinin uzunluklarının çarpımlarının toplamı, köşegenlerinin uzunluklarının çarpımına eşitse, bu dörtgen bir daire içerisine çizilebilir, yani bir kirişler dörtgenidir.
Örnekler
Eşkenar üçgen

Batlamyus Teoremi, sonuç olarak daire içine çizilmiş bir eşkenar üçgene ilişkin güzel bir teoreme ulaşmamıza imkan verir.
Verilen: Bir daire üzerine çizilmiş bir eşkenar üçgen ve daire üzerinde bir nokta.
Noktadan üçgenin en uzak köşesine olan mesafe, noktadan daha yakın iki köşeye olan mesafelerin toplamıdır.
İspat: Hemen Batlamyus teoremini takip edersek:
Kare
Merkezi karenin merkezi olan bir daireye herhangi bir kare çizilebilir. Dört kenarının ortak uzunluğu 
Dikdörtgen

Daha genel olarak, eğer dörtgen, kenarları 


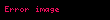
Trigonometrik çalışmasında Batlamyus'un teoremini yoğun bir şekilde kullanan Kopernik, bu sonuca bir 'Porizm' veya apaçık bir sonuç olarak atıfta bulunur:
- Dahası, bir yayı oluşturan kiriş verildiğinde, yarım dairenin geri kalanını altta tutan kirişin de bulunabileceği açıktır (manifestum est).
Beşgen

Daha ilginç bir örnek, düzgün bir beşgendeki kenar uzunluğu 

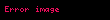
Ongenin kenarı

Şimdi çap 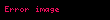
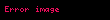
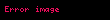
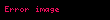



, burada
altın orandır.
böylece daire içine çizilen ongenin kenarı daire çapı cinsinden elde edilir. Dik üçgen 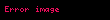


Kopernik'in (Batlamyus'u izleyerek) yazdığı gibi,
- "Verilen bir çemberin çapı, aynı çemberin çevrelediği üçgen, dörtgen, beşgen, altıgen ve ongenin kenarları da verilmiştir."
İspatlar
Üçgenlerin benzerliği ile ispat

bir kirişler dörtgeni olsun.
kirişi üzerinde, çevre açıları
=
ve
üzerinde,
'dir.
üzerinde
noktası
olacak şekilde oluşturulursa;
,
'dir.
- Şimdi, ortak açılardan
,
'ye benzer ve aynı şekilde
de
'ye benzer.
- Böylece
ve
'dir; eşdeğer olarak,
ve
'dır.
- İki eşitlik birbirine ekleyerek
elde ederiz ve bunu çarpanlara ayırmak suretiyle
'yı elde ederiz.
- Ancak
'dır, dolayısıyla
Yazıldığı şekliyle ispat yalnızca basit kirişler dörtgenleri için geçerlidir. Dörtgen kendi kendine kesişiyorsa 

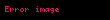
Trigonometrik özdeşliklerle ispat


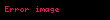




,
,
,
,
ve
olur ve kanıtlanacak orijinal eşitlik aşağıdaki hale dönüşür;
denklemin her iki tarafı da 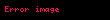
Şimdi toplam formüllerini kullanarak,
ve
Yukarıdaki denklemin her iki tarafının da eşit olduğunu göstermek basittir.
Evirtim ile ispat



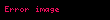
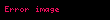
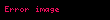

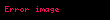
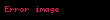
,
,
Önceki ilişkiyi 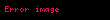
Dörtgen kirişler dörtgeni değilse, 
Karmaşık sayılar kullanarak ispat
ABCD 
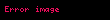

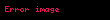
ve
elde edilir.
Kirişler dörtgeni içindeki zıt açılar toplamı 
Bu nedenle, 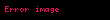
ve
olur.
Dolayısıyla,
'dir.
Burada üçüncü ila son eşitlik, niceliğin zaten gerçek ve pozitif olduğu gerçeğinden kaynaklanır. Q.E.D.
Sonuçlar

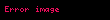

Birim çaplı bir dairede olması durumunda, herhangi bir 
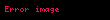
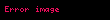

Oluşturulan 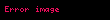

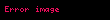
Sonuç 1. Pisagor teoremi
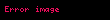
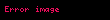
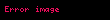
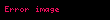
Sonuç 2. Kosinüs yasası

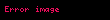
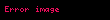
olup, bu durumda Batlamyus teoreminin standart ifadesine dönmek daha kolay olacaktır:
ABC üçgeninin kosinüs kuralı.
Sonuç 3. Sinüs toplam formülü
olsun.
Sonra
Bu nedenle,
Sinüs toplam formülü elde edilir.
Sonuç 4. Sinüs fark formülü

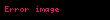
Dolayısıyla,
Sinüs fark formülü elde edilir.
Bu türetme, Batlamyus'un Almagest'te ardından Kopernik tarafından tarihte kayıt altına alınan Üçüncü Teoreme karşılık gelir. Özellikle, bir beşgenin (çevresindeki dairede 36° ile oluşturulan) ve bir altıgenin (çevresindeki dairede 30° ile oluşturulan) kenarları verilirse, 6° ile oluşturulan bir kiriş hesaplanabilir. Bu, kiriş tablolarını hesaplamanın eski yönteminde kritik bir adımdı.
Sonuç 5. Kosinüs toplam formülü
Bu sonuç, Batlamyus'un Almagest'te ardından Kopernik tarafından tarihte kayıt altına alınan Beşinci Teoremin özüdür.
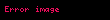
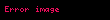
Kosinüs toplam formülü elde edilir.
Modern trigonometrik notasyonumuzun becerisinden yoksun olmasına rağmen, yukarıdaki sonuçlardan, Batlamyus teoreminde (veya daha basitçe İkinci Teoremde) antik dünyanın emrinde son derece esnek ve güçlü bir trigonometrik araca sahip olduğu anlaşılmalıdır. Doğru kiriş tabloları (sinüs tablolarına karşılık gelen) hazırlamak ve bunları kozmosu gördükleri gibi anlama ve haritalama girişimlerinde kullanmak için. Kiriş tabloları Hipparchus tarafından Batlamyus'tan üç yüzyıl önce hazırlandığı için, 'İkinci Teorem'i ve türevlerini bildiğini varsaymalıyız. Eski gök bilimcilerin izinden giden tarih, İskenderiyeli Timocharis'in yıldız kataloğunu kaydeder. Muhtemel göründüğü gibi, bu tür katalogların derlenmesi 'İkinci Teorem'in anlaşılmasını gerektiriyorsa, o zaman ikincisinin gerçek kökenleri daha sonra antik çağın sisleri arasında kaybolur, ancak eski Mısırın gök bilimcilerin, mimarların ve inşaat mühendislerinin bu konuda biraz bilgi sahibi olduğunu varsaymak mantıksız olamaz.
Batlamyus eşitsizliği

Batlamyus teoremindeki denklem, kirişler dörtgeni olmayan dörtgenlerde asla doğru değildir. Batlamyus eşitsizliği bu gerçeğin bir uzantısıdır ve Batlamyus teoreminin daha genel bir biçimidir. Bir 
burada eşitlik, ancak ve ancak dörtgen kirişler dörtgeni ise geçerlidir. Bu özel durum, Batlamyus teoremine eşdeğerdir.
İkinci Batlamyus teoremi
Batlamyus teoremi, kenarları bilinen bir kirişler dörtgeninin köşegenlerin çarpımını verir. Yukarıdaki özdeşlik ise oranlarını verir.
İspat : Bir çevrel çember içine çizilen 

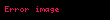
Dörtgenin alanını aynı çevrel çemberi paylaşan iki üçgenin toplamı olarak yazdığımızda, her ayrışma için iki ilişki elde ederiz.
Denkleştirerek, açıklanan formülü elde ederiz.
Sonuç : Köşegenlerin hem çarpımını hem de oranını bildiğimizde, bunların anlık ifadelerini çıkarıyoruz:
Ayrıca bakınız
Notlar
- ^ C. Ptolemy, Almagest, Book 1, Chapter 10.
- ^ Wilson, Jim. . 15 Aralık 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Nisan 2009.
- ^ "De Revolutionibus Orbium Coelestium: Page 37". 3 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.. Bu sayfanın son iki satırına bakın. Copernicus, Ptolemy'nin teoremini şu şekilde ifade eder: "Theorema Secundum". 3 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.
- ^ . 10 Mayıs 2008 tarihinde kaynağından arşivlendi. in . 26 Temmuz 2011 tarihinde kaynağından arşivlendi.
proves by similar triangles the same result: namely that length a (the side of the pentagon) divides length b (joining alternate vertices of the pentagon) in "mean and extreme ratio".
- ^ And in analogous fashion . 10 Mayıs 2008 tarihinde kaynağından arşivlendi. in . 26 Temmuz 2011 tarihinde kaynağından arşivlendi.
proves by similar triangles that length c (the side of the decagon) divides the radius in "mean and extreme ratio".
- ^ An interesting article on the construction of a regular pentagon and determination of side length can be found at the following reference
- ^ "De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Primum". 3 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.
- ^ Alsina (2010), Charming Proofs: A Journey Into Elegant Mathematics, Dolciani Mathematical Expositions, 42, Mathematical Association of America, s. 112, ISBN , 15 Eylül 2015 tarihinde kaynağından , erişim tarihi: 24 Eylül 2020
- ^ In De Revolutionibus Orbium Coelestium, Copernicus does not refer to Pythagoras's theorem by name but uses the term 'Porism' – a word which in this particular context would appear to denote an observation on – or obvious consequence of – another existing theorem. The 'Porism' can be viewed on pages 36 and 37 3 Nisan 2021 tarihinde Wayback Machine sitesinde . of DROC (Harvard electronic copy)
- ^ a b . 30 Aralık 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Eylül 2020.
- ^ "Üçüncü Teorem". 3 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.
- ^ To understand the Third Theorem, compare the Copernican diagram shown on page 39 of the . 13 Temmuz 2006 tarihinde kaynağından arşivlendi. of De Revolutionibus to that for the derivation of
found in the above . cut-the-knot. 30 Aralık 2010 tarihinde kaynağından (web page) arşivlendi.
- ^ "Beşinci Teorem". 3 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.
- ^ "İkinci Teorem". 3 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.
Kaynakça
- Coxeter, HSM ve SL Greitzer (1967) "Ptolemy Teoremi ve Uzantıları." Geometry Revisited içinde §2.6, Mathematical Association of America s. 42–43.
- Copernicus (1543) De Revolutionibus Orbium Coelestium, Stephen Hawking, Penguin Books tarafından düzenlenen On the Shoulders of Giants'da (2002) bulunan İngilizce çevirisi
- Amarasinghe, GWIS (2013), (PDF), Global Journal of Advanced Research on Classical and Modern Geometries (GJARCMG), 2 (1), ss. 20-25, 15 Temmuz 2020 tarihinde kaynağından (pdf) arşivlendi
Dış bağlantılar
- Halil İbrahim Yazıcı & Muhammed Enis Şen (2014), "Ptolemy Teoremi ve Uygulamaları" (PDF), Özel Darüşşafaka Lisesi Salih Zeki V. Matematik Araştırma Projeleri Yarışması
- . 30 Eylül 2019 tarihinde kaynağından arşivlendi.
- . 31 Ocak 2020 tarihinde kaynağından arşivlendi.
- "Ptolemy's Table of Chords". E-World. 1994. 17 Aralık 2019 tarihinde kaynağından . Erişim tarihi: 24 Eylül 2020.
- "Batlamyus Teoremi". Cut-the-Knot. 29 Mart 2019 tarihinde kaynağından arşivlendi.
- . Cut-the-Knot. 30 Aralık 2010 tarihinde kaynağından arşivlendi.
- . PlanetMath. 24 Temmuz 2011 tarihinde kaynağından arşivlendi.
- Eric W. Weisstein, Batlamyus Eşitsizliği (MathWorld)
- . Harvard. 13 Temmuz 2006 tarihinde kaynağından arşivlendi.
- . 5 Temmuz 2008 tarihinde kaynağından arşivlendi.
- Jay Warendorff. . Wolfram Demonstration Project. 8 Eylül 2019 tarihinde kaynağından arşivlendi.
- . 26 Temmuz 2011 tarihinde kaynağından arşivlendi.
- . 9 Nisan 2008 tarihinde kaynağından arşivlendi.
- . 18 Nisan 2016 tarihinde kaynağından arşivlendi.
Konuyla ilgili yayınlar
- Hung, Tran Quang (2019), "Generalization of Ptolemy's Theorem'", Journal of Science and Arts, Targoviste, 19 (2), ss. 275-280
- N. S. Astapov & I. S. Astapov (2019), "The variety of generalizations of the Ptolemy's theorem", Dal'nevost. Mat. Zh., 19 (2), ss. 129-137
- Ricahrd G. Swan, Ptolemy's Theorem And Its Converse (PDF), 18 Haziran 2021 tarihinde kaynağından (PDF), erişim tarihi: 8 Kasım 2020
- Shay Gueron (2002), Two Applications of the Generalized Ptolemy Theorem (PDF), 5 Haziran 2020 tarihinde kaynağından (PDF), erişim tarihi: 8 Kasım 2020
- Erwin Just Norman Schaumberger, A Vector Approach to Ptolemy's Theorem (PDF), 22 Şubat 2016 tarihinde kaynağından (PDF), erişim tarihi: 8 Kasım 2020
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Oklid geometrisinde Batlamyus teoremi bir koseleri ortak bir daire uzerinde yer alan bir dortgen dort kenari ile iki kosegeni arasindaki bir iliskiyi gosteridir Teorem Yunan astronom ve matematikci Batlamyus un Claudius Ptolemaeus adini almistir Batlamyus teoremi astronomiye uyguladigi trigonometrik bir tablo olan kirisler tablosunu olusturmaya yardimci olarak kullandi Batlamyus teoremi bir kirisler dortgeninin uzunluklari arasindaki iliskiyi gosterir Kirisler dortgenin koseleri sirayla A displaystyle A B displaystyle B C displaystyle C ve D displaystyle D ise teorem sunu belirtir AC BD AB CD BC AD displaystyle overline AC cdot overline BD overline AB cdot overline CD overline BC cdot overline AD Burada dikey cizgiler ile gosterim adlandirilmis koseler arasindaki cizgi parcalarinin uzunluklarini belirtmektedir Geometri baglaminda yukaridaki esitlik genellikle basitce soyle yazilir AC BD AB CD BC AD displaystyle AC cdot BD AB cdot CD BC cdot AD Bu iliski sozlu olarak su sekilde ifade edilebilir Eger bir dortgen bir dairenin icine cizilebiliyorsa kosegenlerinin uzunluklarinin carpimi karsit kenarlarin ciftlerinin uzunluklarinin carpimlarinin toplamina esittir Dahasi Batlamyus teoreminin tersi de dogrudur Bir dortgende karsit iki kenar ciftinin uzunluklarinin carpimlarinin toplami kosegenlerinin uzunluklarinin carpimina esitse bu dortgen bir daire icerisine cizilebilir yani bir kirisler dortgenidir OrneklerEskenar ucgen Eskenar ucgen Batlamyus Teoremi sonuc olarak daire icine cizilmis bir eskenar ucgene iliskin guzel bir teoreme ulasmamiza imkan verir Verilen Bir daire uzerine cizilmis bir eskenar ucgen ve daire uzerinde bir nokta Noktadan ucgenin en uzak kosesine olan mesafe noktadan daha yakin iki koseye olan mesafelerin toplamidir Ispat Hemen Batlamyus teoremini takip edersek qs ps rs q p r displaystyle qs ps rs Rightarrow q p r Kare Merkezi karenin merkezi olan bir daireye herhangi bir kare cizilebilir Dort kenarinin ortak uzunlugu a displaystyle a ya esitse daha sonra kosegenin uzunlugu a2 displaystyle a sqrt 2 ye esittir Pisagor teoremine gore ve bu iliski acikca gecerlidir Dikdortgen Pisagor teoremi manifestum est Kopernik Daha genel olarak eger dortgen kenarlari a displaystyle a ve b displaystyle b ve kosegenleri d displaystyle d olan bir dikdortgen verilirse Batlamyus teoremi Pisagor teoremine indirgenir Bu durumda dairenin merkezi kosegenlerin kesisme noktasiyla cakisir Bu durumda kosegenlerinin carpimi d2 displaystyle d 2 olarak bulunur Batlamyus esitligine gore sag taraftaki toplam a2 b2 displaystyle a 2 b 2 dir Trigonometrik calismasinda Batlamyus un teoremini yogun bir sekilde kullanan Kopernik bu sonuca bir Porizm veya apacik bir sonuc olarak atifta bulunur Dahasi bir yayi olusturan kiris verildiginde yarim dairenin geri kalanini altta tutan kirisin de bulunabilecegi aciktir manifestum est Besgen Altin oran Batlamyus teoreminin bu uygulamasindan gelir Daha ilginc bir ornek duzgun bir besgendeki kenar uzunlugu a displaystyle a ile 5 kirisin ortak uzunlugu b displaystyle b arasindaki iliskidir Bu durumda b2 a2 ab displaystyle b 2 a 2 ab altin orani veren iliskidir f ba 1 52 displaystyle varphi b over a 1 sqrt 5 over 2 Ongenin kenari Daire ile cevrelenen ongenin kenari Simdi cap AF displaystyle AF DC displaystyle DC yi ikiye bolerek cizilirse boylece DF displaystyle DF ve CF displaystyle CF daire icine cizilen bir ongenin c displaystyle c kenarlaridir Batlamyus teoremi tekrar uygulanirsa bu kez kosegenlerinden biri olarak d displaystyle d capina sahip kirisler dortgeni ADFC displaystyle ADFC ye ad 2bc displaystyle ad 2bc ad 2fac displaystyle Rightarrow ad 2 varphi ac burada f displaystyle varphi altin orandir c d2f displaystyle Rightarrow c frac d 2 varphi boylece daire icine cizilen ongenin kenari daire capi cinsinden elde edilir Dik ucgen AFD displaystyle triangle AFD ye uygulanan Pisagor teoremi cap olarak b displaystyle b uzunlugunu verir ve bundan sonra besgenin kenari a displaystyle a olarak hesaplanir a bf b f 1 displaystyle a frac b varphi b varphi 1 dd Kopernik in Batlamyus u izleyerek yazdigi gibi Verilen bir cemberin capi ayni cemberin cevreledigi ucgen dortgen besgen altigen ve ongenin kenarlari da verilmistir IspatlarUcgenlerin benzerligi ile ispat Batlamyus teoreminin bir kaniti icin cizimABCD displaystyle ABCD bir kirisler dortgeni olsun BC displaystyle BC kirisi uzerinde cevre acilari BAC displaystyle angle BAC BDC displaystyle angle BDC ve AB displaystyle AB uzerinde ADB ACB displaystyle angle ADB angle ACB dir AC displaystyle AC uzerinde K displaystyle K noktasi ABK CBD displaystyle angle ABK angle CBD olacak sekilde olusturulursa ABK CBK ABC CBD ABD displaystyle angle ABK angle CBK angle ABC angle CBD angle ABD CBK ABD displaystyle angle CBK angle ABD dir Simdi ortak acilardan DABK displaystyle Delta ABK DDBC displaystyle Delta DBC ye benzer ve ayni sekilde DABD displaystyle Delta ABD de DKBC displaystyle Delta KBC ye benzer Boylece AKAB CDBD displaystyle frac AK AB frac CD BD ve CKBC DABD displaystyle frac CK BC frac DA BD dir esdeger olarak AK BD AB CD displaystyle AK cdot BD AB cdot CD ve CK BD BC DA displaystyle CK cdot BD BC cdot DA dir Iki esitlik birbirine ekleyerek AK BD CK BD AB CD BC DA displaystyle AK cdot BD CK cdot BD AB cdot CD BC cdot DA elde ederiz ve bunu carpanlara ayirmak suretiyle AK CK BD AB CD BC DA displaystyle AK CK cdot BD AB cdot CD BC cdot DA yi elde ederiz Ancak AK CK AC displaystyle AK CK AC dir dolayisiyla AC BD AB CD BC DA displaystyle AC cdot BD AB cdot CD BC cdot DA QED Yazildigi sekliyle ispat yalnizca basit kirisler dortgenleri icin gecerlidir Dortgen kendi kendine kesisiyorsa K displaystyle K AC displaystyle AC cizgi parcasinin disinda yer alacaktir Ancak bu durumda AK CK AC displaystyle AK CK pm AC beklenen sonucu verir Trigonometrik ozdesliklerle ispat AB displaystyle AB BC displaystyle BC ve CD displaystyle CD tarafindan olusturulan cevre acilar sirasiyla a displaystyle alpha b displaystyle beta ve g displaystyle gamma ve cemberin yaricapi R displaystyle R olsun O zaman AB 2Rsin a displaystyle AB 2R sin alpha BC 2Rsin b displaystyle BC 2R sin beta CD 2Rsin g displaystyle CD 2R sin gamma AD 2Rsin 180 a b g displaystyle AD 2R sin 180 alpha beta gamma AC 2Rsin a b displaystyle AC 2R sin alpha beta ve BD 2Rsin b g displaystyle BD 2R sin beta gamma olur ve kanitlanacak orijinal esitlik asagidaki hale donusur sin a b sin b g sin asin g sin bsin a b g displaystyle sin alpha beta sin beta gamma sin alpha sin gamma sin beta sin alpha beta gamma denklemin her iki tarafi da 4R2 displaystyle 4R 2 carpanina bolunerek sadelesti Simdi toplam formullerini kullanarak sin x y sin xcos y cos xsin y displaystyle sin x y sin x cos y cos x sin y ve cos x y cos xcos y sin xsin y displaystyle cos x y cos x cos y sin x sin y Yukaridaki denklemin her iki tarafinin da esit oldugunu gostermek basittir sin asin bcos bcos g sin acos2 bsin g cos asin2 bcos g cos asin bcos bsin g displaystyle begin aligned amp sin alpha sin beta cos beta cos gamma sin alpha cos 2 beta sin gamma amp cos alpha sin 2 beta cos gamma cos alpha sin beta cos beta sin gamma end aligned Q E D Evirtim ile ispat Daire evirtimi yoluyla Batlamyus teoreminin kaniti ABCD displaystyle ABCD nin cevrel cemberi bir dogruya evirtildigine sekle bakin gore merkezi D displaystyle D olan yardimci bir G displaystyle Gamma dairesi secin Sonra A B B C A C displaystyle A B B C A C olur Genelligi kaybetmeden G displaystyle Gamma nin yaricapini 1 displaystyle 1 alalim Sonra A B B C displaystyle A B B C ve A C displaystyle A C sirasiyla asagidaki sekilde ifade edilebilir AB DB DA displaystyle frac AB cdot DB DA BC DB DC displaystyle frac BC cdot DB DC AC DC DA displaystyle frac AC cdot DC DA Onceki iliskiyi DA DCDB displaystyle frac DA cdot DC DB ile carpar ve DC DB DBDC displaystyle frac DC DB frac DB DC esitligini kullanirsak Batlamyus un esitligini elde ederiz Q E D Dortgen kirisler dortgeni degilse A displaystyle A B displaystyle B ve C displaystyle C nun bir ucgen olusturduguna ve dolayisiyla A B B C gt A C displaystyle A B B C gt A C olduguna dikkat edin bize asagida sunulan Batlamyus Esitsizliginin cok basit bir kaniti verir Karmasik sayilar kullanarak ispat ABCD C displaystyle scriptstyle mathbb C de bir daire etrafinda saat yonunde A zA D zD displaystyle A mapsto z A ldots D mapsto z D zA zD C displaystyle z A ldots z D in scriptstyle mathbb C olacak sekilde duzenlensin Karmasik bir sayinin kutupsal formundan z z eiarg z displaystyle z vert z vert e i arg z yazilabilir Buradan da ABC arg zC zB arg zA zB mod2p displaystyle angle ABC arg z C z B arg z A z B pmod 2 pi quad ve CDA arg zA zD arg zC zD mod2p displaystyle angle CDA arg z A z D arg z C z D pmod 2 pi elde edilir Kirisler dortgeni icindeki zit acilar toplami p displaystyle pi oldugundan 0 p ABC CDA mod2p arg 1 arg zC zB arg zA zB arg zA zD arg zC zD mod2p arg zA zD zB zC arg zA zB zC zD displaystyle begin aligned 0 amp pi angle ABC angle CDA pmod 2 pi amp arg 1 left arg z C z B arg z A z B right left arg z A z D arg z C z D right pmod 2 pi amp arg left z A z D z B z C right arg left z A z B z C z D right end aligned Bu nedenle f arg zA zB zC zD arg zA zD zB zC displaystyle varphi arg left z A z B z C z D right arg left z A z D z B z C right Boylece zA zB zC zD zA zB zC zD eif displaystyle left z A z B z C z D right z A z B z C z D e i varphi quad ve zA zD zB zC zA zD zB zC eif displaystyle left z A z D z B z C right z A z D z B z C e i varphi olur Dolayisiyla AB CD AD BC zA zB zC zD zA zD zB zC zA zB zC zD zA zD zB zC zA zB zC zD eif zA zD zB zC eif zA zC zB zD eif zA zC zB zD eif zA zC zB zD eif AC BD displaystyle begin aligned overline AB cdot overline CD overline AD cdot overline BC amp left z A z B right left z C z D right left z A z D right left z B z C right amp left z A z B z C z D right left z A z D z B z C right amp z A z B z C z D e i varphi z A z D z B z C e i varphi amp z A z C z B z D e i varphi amp left z A z C z B z D e i varphi right amp left z A z C left right z B z D right left e i varphi right amp overline AC cdot overline BD end aligned dir Burada ucuncu ila son esitlik niceligin zaten gercek ve pozitif oldugu gerceginden kaynaklanir Q E D Sonuclar S1 sin 81 displaystyle S 1 sin theta 1 Sonuc 1 Pisagor teoremi Birim capli bir dairede olmasi durumunda herhangi bir ABCD displaystyle ABCD kirisler dortgeninin kenarlari S1 S2 S3 S4 displaystyle S 1 S 2 S 3 S 4 bu kenarlar tarafindan olusturulan 81 82 83 displaystyle theta 1 theta 2 theta 3 ve 84 displaystyle theta 4 acilarin sinuslerine sayisal olarak esittir Benzer sekilde kosegenler hangi aci ciftini olusturursa olustursunlar sinuslerinin toplaminin esittir Daha sonra Batlamyus Teoremini asagidaki trigonometrik bicimde yazabiliriz sin 81sin 83 sin 82sin 84 sin 81 82 sin 81 84 displaystyle sin theta 1 sin theta 3 sin theta 2 sin theta 4 sin theta 1 theta 2 sin theta 1 theta 4 Olusturulan 81 82 83 displaystyle theta 1 theta 2 theta 3 ve 84 displaystyle theta 4 acilarina belirli kosullari uyguladigimizda yukaridakileri baslangic noktamiz olarak kullanarak bir dizi onemli sonuc cikarmak mumkundur Asagidakilerde acilarin toplaminin 81 82 83 84 180 displaystyle theta 1 theta 2 theta 3 theta 4 180 circ oldugunu akilda bulundurmak faydali olacaktir Sonuc 1 Pisagor teoremi 81 83 displaystyle theta 1 theta 3 ve 82 84 displaystyle theta 2 theta 4 olsun Sonra 81 82 83 84 90 displaystyle theta 1 theta 2 theta 3 theta 4 90 circ cunku kirisler dortgeninin zit acilari butunlerdir Ardindan sin 81sin 83 sin 82sin 84 sin 81 82 sin 81 84 displaystyle sin theta 1 sin theta 3 sin theta 2 sin theta 4 sin theta 1 theta 2 sin theta 1 theta 4 sin2 81 sin2 82 sin2 81 82 displaystyle sin 2 theta 1 sin 2 theta 2 sin 2 theta 1 theta 2 sin2 81 cos2 81 1 displaystyle sin 2 theta 1 cos 2 theta 1 1 Sonuc 2 Kosinus yasasi Sonuc 2 Kosinus yasasi 82 84 displaystyle theta 2 theta 4 olsun Sonuc 1 in dikdortgeni simdi esit kosegenlere ve bir cift esit kenara sahip simetrik bir yamuktur Paralel kenarlarin uzunluklari 2x displaystyle 2x birim farklilik gosterir Burada x S2cos 82 83 displaystyle x S 2 cos theta 2 theta 3 olup bu durumda Batlamyus teoreminin standart ifadesine donmek daha kolay olacaktir S1S3 S2S4 AC BD S1S3 S22 AC 2 S1 S1 2S2cos 82 83 S22 AC 2 S12 S22 2S1S2cos 82 83 AC 2 displaystyle begin array lcl S 1 S 3 S 2 S 4 overline AC cdot overline BD Rightarrow S 1 S 3 S 2 2 overline AC 2 Rightarrow S 1 S 1 2S 2 cos theta 2 theta 3 S 2 2 overline AC 2 Rightarrow S 1 2 S 2 2 2S 1 S 2 cos theta 2 theta 3 overline AC 2 end array ABC ucgeninin kosinus kurali Sonuc 3 Sinus toplam formulu 81 82 83 84 90 displaystyle theta 1 theta 2 theta 3 theta 4 90 circ olsun Sonra sin 81sin 83 sin 82sin 84 sin 83 82 sin 83 84 displaystyle sin theta 1 sin theta 3 sin theta 2 sin theta 4 sin theta 3 theta 2 sin theta 3 theta 4 Bu nedenle cos 82sin 83 sin 82cos 83 sin 83 82 1 displaystyle cos theta 2 sin theta 3 sin theta 2 cos theta 3 sin theta 3 theta 2 times 1 Sinus toplam formulu elde edilir Sonuc 4 Sinus fark formulu 81 90 displaystyle theta 1 90 circ olsun Sonra 82 83 84 90 displaystyle theta 2 theta 3 theta 4 90 circ Dolayisiyla sin 81sin 83 sin 82sin 84 sin 83 82 sin 83 84 displaystyle sin theta 1 sin theta 3 sin theta 2 sin theta 4 sin theta 3 theta 2 sin theta 3 theta 4 sin 83 sin 82cos 82 83 sin 83 82 cos 82 displaystyle sin theta 3 sin theta 2 cos theta 2 theta 3 sin theta 3 theta 2 cos theta 2 sin 83 sin 83 82 cos 82 cos 82 83 sin 82 displaystyle sin theta 3 sin theta 3 theta 2 cos theta 2 cos theta 2 theta 3 sin theta 2 Sinus fark formulu elde edilir Bu turetme Batlamyus un Almagest te ardindan Kopernik tarafindan tarihte kayit altina alinan Ucuncu Teoreme karsilik gelir Ozellikle bir besgenin cevresindeki dairede 36 ile olusturulan ve bir altigenin cevresindeki dairede 30 ile olusturulan kenarlari verilirse 6 ile olusturulan bir kiris hesaplanabilir Bu kiris tablolarini hesaplamanin eski yonteminde kritik bir adimdi Sonuc 5 Kosinus toplam formulu Bu sonuc Batlamyus un Almagest te ardindan Kopernik tarafindan tarihte kayit altina alinan Besinci Teoremin ozudur 83 90 displaystyle theta 3 90 circ olsun Sonra81 82 84 90 displaystyle theta 1 theta 2 theta 4 90 circ Bu nedenle sin 81sin 83 sin 82sin 84 sin 83 82 sin 83 84 displaystyle sin theta 1 sin theta 3 sin theta 2 sin theta 4 sin theta 3 theta 2 sin theta 3 theta 4 cos 82 84 sin 82sin 84 cos 82cos 84 displaystyle cos theta 2 theta 4 sin theta 2 sin theta 4 cos theta 2 cos theta 4 cos 82 84 cos 82cos 84 sin 82sin 84 displaystyle cos theta 2 theta 4 cos theta 2 cos theta 4 sin theta 2 sin theta 4 Kosinus toplam formulu elde edilir Modern trigonometrik notasyonumuzun becerisinden yoksun olmasina ragmen yukaridaki sonuclardan Batlamyus teoreminde veya daha basitce Ikinci Teoremde antik dunyanin emrinde son derece esnek ve guclu bir trigonometrik araca sahip oldugu anlasilmalidir Dogru kiris tablolari sinus tablolarina karsilik gelen hazirlamak ve bunlari kozmosu gordukleri gibi anlama ve haritalama girisimlerinde kullanmak icin Kiris tablolari Hipparchus tarafindan Batlamyus tan uc yuzyil once hazirlandigi icin Ikinci Teorem i ve turevlerini bildigini varsaymaliyiz Eski gok bilimcilerin izinden giden tarih Iskenderiyeli Timocharis in yildiz katalogunu kaydeder Muhtemel gorundugu gibi bu tur kataloglarin derlenmesi Ikinci Teorem in anlasilmasini gerektiriyorsa o zaman ikincisinin gercek kokenleri daha sonra antik cagin sisleri arasinda kaybolur ancak eski Misirin gok bilimcilerin mimarlarin ve insaat muhendislerinin bu konuda biraz bilgi sahibi oldugunu varsaymak mantiksiz olamaz Batlamyus esitsizligiBu bir kirisler dortgeni degildir Esitlik burada asla gecerli degildir ve Batlamyus esitsizliginin gosterdigi yonde esit degildir Batlamyus teoremindeki denklem kirisler dortgeni olmayan dortgenlerde asla dogru degildir Batlamyus esitsizligi bu gercegin bir uzantisidir ve Batlamyus teoreminin daha genel bir bicimidir Bir ABCD displaystyle ABCD dortgeni verildiginde AB CD BC DA AC BD displaystyle overline AB cdot overline CD overline BC cdot overline DA geq overline AC cdot overline BD burada esitlik ancak ve ancak dortgen kirisler dortgeni ise gecerlidir Bu ozel durum Batlamyus teoremine esdegerdir Ikinci Batlamyus teoremiACBD AB DA BC CDAB BC DA CD displaystyle frac AC BD frac AB cdot DA BC cdot CD AB cdot BC DA cdot CD Batlamyus teoremi kenarlari bilinen bir kirisler dortgeninin kosegenlerin carpimini verir Yukaridaki ozdeslik ise oranlarini verir Ispat Bir cevrel cember icine cizilen ABC displaystyle ABC ucgenin alani R displaystyle R cap olmak uzere A AB BC CA4R displaystyle mathcal A frac AB cdot BC cdot CA 4R dir Dortgenin alanini ayni cevrel cemberi paylasan iki ucgenin toplami olarak yazdigimizda her ayrisma icin iki iliski elde ederiz Atop AB BC CA4R CD DA AC4R AC AB BC CD DA 4R displaystyle mathcal A text top frac AB cdot BC cdot CA 4R frac CD cdot DA cdot AC 4R frac AC cdot AB cdot BC CD cdot DA 4R Atop AB BD DA4R BC CD DB4R BD AB DA BC CD 4R displaystyle mathcal A text top frac AB cdot BD cdot DA 4R frac BC cdot CD cdot DB 4R frac BD cdot AB cdot DA BC cdot CD 4R Denklestirerek aciklanan formulu elde ederiz Sonuc Kosegenlerin hem carpimini hem de oranini bildigimizde bunlarin anlik ifadelerini cikariyoruz AC2 AC BD ACBD AB CD BC DA AB DA BC CDAB BC DA CDBD2 AC BDACBD AB CD BC DA AB BC DA CDAB DA BC CD displaystyle begin aligned AC 2 amp AC cdot BD cdot frac AC BD AB cdot CD BC cdot DA frac AB cdot DA BC cdot CD AB cdot BC DA cdot CD 8pt BD 2 amp frac AC cdot BD frac AC BD AB cdot CD BC cdot DA frac AB cdot BC DA cdot CD AB cdot DA BC cdot CD end aligned Ayrica bakinizCasey teoremi Yunan matematigiNotlar C Ptolemy Almagest Book 1 Chapter 10 Wilson Jim 15 Aralik 2017 tarihinde kaynagindan arsivlendi Erisim tarihi 8 Nisan 2009 De Revolutionibus Orbium Coelestium Page 37 3 Nisan 2021 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 Bu sayfanin son iki satirina bakin Copernicus Ptolemy nin teoremini su sekilde ifade eder Theorema Secundum 3 Nisan 2021 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 10 Mayis 2008 tarihinde kaynagindan arsivlendi in 26 Temmuz 2011 tarihinde kaynagindan arsivlendi proves by similar triangles the same result namely that length a the side of the pentagon divides length b joining alternate vertices of the pentagon in mean and extreme ratio And in analogous fashion 10 Mayis 2008 tarihinde kaynagindan arsivlendi in 26 Temmuz 2011 tarihinde kaynagindan arsivlendi proves by similar triangles that length c the side of the decagon divides the radius in mean and extreme ratio An interesting article on the construction of a regular pentagon and determination of side length can be found at the following reference De Revolutionibus Orbium Coelestium Liber Primus Theorema Primum 3 Nisan 2021 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 Alsina 2010 Charming Proofs A Journey Into Elegant Mathematics Dolciani Mathematical Expositions 42 Mathematical Association of America s 112 ISBN 9780883853481 15 Eylul 2015 tarihinde kaynagindan erisim tarihi 24 Eylul 2020 In De Revolutionibus Orbium Coelestium Copernicus does not refer to Pythagoras s theorem by name but uses the term Porism a word which in this particular context would appear to denote an observation on or obvious consequence of another existing theorem The Porism can be viewed on pages 36 and 37 3 Nisan 2021 tarihinde Wayback Machine sitesinde of DROC Harvard electronic copy a b 30 Aralik 2010 tarihinde kaynagindan arsivlendi Erisim tarihi 24 Eylul 2020 Ucuncu Teorem 3 Nisan 2021 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 To understand the Third Theorem compare the Copernican diagram shown on page 39 of the 13 Temmuz 2006 tarihinde kaynagindan arsivlendi of De Revolutionibus to that for the derivation of sin A B displaystyle sin A B found in the above cut the knot 30 Aralik 2010 tarihinde kaynagindan web page arsivlendi Besinci Teorem 3 Nisan 2021 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 Ikinci Teorem 3 Nisan 2021 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 KaynakcaCoxeter HSM ve SL Greitzer 1967 Ptolemy Teoremi ve Uzantilari Geometry Revisited icinde 2 6 Mathematical Association of America s 42 43 Copernicus 1543 De Revolutionibus Orbium Coelestium Stephen Hawking Penguin Books tarafindan duzenlenen On the Shoulders of Giants da 2002 bulunan Ingilizce cevirisi0 14 101571 3 Amarasinghe GWIS 2013 PDF Global Journal of Advanced Research on Classical and Modern Geometries GJARCMG 2 1 ss 20 25 15 Temmuz 2020 tarihinde kaynagindan pdf arsivlendi Dis baglantilarHalil Ibrahim Yazici amp Muhammed Enis Sen 2014 Ptolemy Teoremi ve Uygulamalari PDF Ozel Darussafaka Lisesi Salih Zeki V Matematik Arastirma Projeleri Yarismasi 30 Eylul 2019 tarihinde kaynagindan arsivlendi 31 Ocak 2020 tarihinde kaynagindan arsivlendi Ptolemy s Table of Chords E World 1994 17 Aralik 2019 tarihinde kaynagindan Erisim tarihi 24 Eylul 2020 Batlamyus Teoremi Cut the Knot 29 Mart 2019 tarihinde kaynagindan arsivlendi Cut the Knot 30 Aralik 2010 tarihinde kaynagindan arsivlendi PlanetMath 24 Temmuz 2011 tarihinde kaynagindan arsivlendi Eric W Weisstein Batlamyus Esitsizligi MathWorld Harvard 13 Temmuz 2006 tarihinde kaynagindan arsivlendi 5 Temmuz 2008 tarihinde kaynagindan arsivlendi Jay Warendorff Wolfram Demonstration Project 8 Eylul 2019 tarihinde kaynagindan arsivlendi 26 Temmuz 2011 tarihinde kaynagindan arsivlendi 9 Nisan 2008 tarihinde kaynagindan arsivlendi 18 Nisan 2016 tarihinde kaynagindan arsivlendi Konuyla ilgili yayinlarHung Tran Quang 2019 Generalization of Ptolemy s Theorem Journal of Science and Arts Targoviste 19 2 ss 275 280 N S Astapov amp I S Astapov 2019 The variety of generalizations of the Ptolemy s theorem Dal nevost Mat Zh 19 2 ss 129 137 Ricahrd G Swan Ptolemy s Theorem And Its Converse PDF 18 Haziran 2021 tarihinde kaynagindan PDF erisim tarihi 8 Kasim 2020 Shay Gueron 2002 Two Applications of the Generalized Ptolemy Theorem PDF 5 Haziran 2020 tarihinde kaynagindan PDF erisim tarihi 8 Kasim 2020 Erwin Just Norman Schaumberger A Vector Approach to Ptolemy s Theorem PDF 22 Subat 2016 tarihinde kaynagindan PDF erisim tarihi 8 Kasim 2020
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans