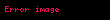Matematiğin bir alt dalı olan çok değişkenli karmaşık analizde Bergman-Weil formülü, çok değişkenli holomorf fonksiyonların integral temsillerinden biridir. Bergman-Weil formülü aynı zamanda Cauchy integral formülünü birde fazla karmaşık boyuta genelleştirir. Stefan Bergman ve André Weil tarafından literatüre sokulmuştur.
İfadesi
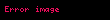






tüm 



olur. Burada, toplam 


 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
Notlar
Kaynaklar
- Bergmann, S. (1936), "Über eine Integraldarstellung von Funktionen zweier komplexer Veränderlichen", , New Series (Almanca), 1 (43) (6), ss. 851-862, JFM 62.1220.04, Zbl 0016.17001.
- Weil, André (1935), "L'intégrale de Cauchy et les fonctions de plusieurs variables", , 111 (1), ss. 178-182, doi:10.1007/BF01472212, ISSN 0025-5831, JFM 61.0371.03, MR 1512987, Zbl 0011.12301.
Dış bağlantılar
- Encyclopedia of Mathematics sitesinde Evgenii Mikhailovich Chirka tarafından yazılmış "Bergman-Weil temsili" sayfası
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan cok degiskenli karmasik analizde Bergman Weil formulu cok degiskenli holomorf fonksiyonlarin integral temsillerinden biridir Bergman Weil formulu ayni zamanda Cauchy integral formulunu birde fazla karmasik boyuta genellestirir Stefan Bergman ve Andre Weil tarafindan literature sokulmustur IfadesiW Cn displaystyle Omega subset mathbb C n de bir bolge P displaystyle P ise W displaystyle Omega uzerinde tanimli holomorf f1 f2 fn displaystyle f 1 f 2 cdots f n fonksiyonlari tarafindan W displaystyle Omega icinde goreceli tikiz kalacak sekilde tanimlanmis analtik cokyuzlu olsun O halde Hefer teoremi sayesinde W W displaystyle Omega times Omega uzerinde holomorf olacak sekilde gjk displaystyle g jk fonksiyonlari vardir oyle ki fj z fj w k 1n zk wk gjk w z displaystyle f j z f j w sum k 1 n z k w k g jk w z tum z w W displaystyle z w in Omega icin yazilabilir W displaystyle overline Omega ustunde surekli ve W displaystyle Omega icinde holomorf olan bir f displaystyle f fonksiyonu olsun O zaman f z 1 2pi n f w det gjkl l 1n fkl w fkl z dw displaystyle f z frac 1 2 pi i n sum int frac f w det g jk l prod l 1 n f k l w f k l z dw olur Burada toplam k1 lt lt kn displaystyle k 1 lt cdots lt k n uzerinden integral de n boyutlu yuzeylerde integral yonu uygun olacak sekilde alinmaktadir dw displaystyle dw ise dw1 dwn displaystyle dw 1 wedge cdots dw n olarak taniimlidir Bu integral temsilinde determinanti tanimli kilmak icin ek sartlar getirmek gerekebilir Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz Notlar Bergmann 1936 Weil 1935 KaynaklarBergmann S 1936 Uber eine Integraldarstellung von Funktionen zweier komplexer Veranderlichen New Series Almanca 1 43 6 ss 851 862 JFM 62 1220 04 Zbl 0016 17001 Weil Andre 1935 L integrale de Cauchy et les fonctions de plusieurs variables 111 1 ss 178 182 doi 10 1007 BF01472212 ISSN 0025 5831 JFM 61 0371 03 MR 1512987 Zbl 0011 12301 Dis baglantilarEncyclopedia of Mathematics sitesinde Evgenii Mikhailovich Chirka tarafindan yazilmis Bergman Weil temsili sayfasi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State