Matematiğin bir alanı olan çok değişkenli kompleks analizde, Bergman çekirdeği, karesi integrallenebilir holomorf fonksiyonlardan oluşan Hilbert uzayının (yani Bergman uzayının) doğuran çekirdeğidir. Stefan Bergman'ın ardından isimlendirilmiştir.
Tanım
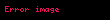





Hilbert uzayıdır:
- Öncelikle, Bergman uzayı, tanımı gereği yine bir Hilbert uzayı olan
nin doğrusal bir altuzayıdır.
- Aynı zamanda, Bergman uzayı,
içinde kapalıdır. Bu yüzden, kendi başına da tam bir metrik uzaydır. Bu uzayın kapalı olmasının sebebi
nin her tıkız alt kümesi için
eşitsizliğinin sağlanmasıdır. Bu halde, bir holomorf fonksiyon dizisinin
içindeki yakınsaklığı tıkız kümeler üzerindeki düzgün yakınsaklığa (yani ) dönüşür. Böylelikle, bu dizinin limiti de holomorf olur.
zaten tam olduğu için, limitin kare integrallenebilir olduğu bilinmektedir. O yüzden, limit fonksiyonu da
içindedir.
- Öncelikle, Bergman uzayı, tanımı gereği yine bir Hilbert uzayı olan
- Yukarıda bahsedilen
eşitsizliğinin
nin her tıkız altkümesinde sağlanması, aynı zamanda
içindeki her
noktası için,
gönderiminin bir sürekli doğrusal operatör olduğunu da gösterir. Bir başka deyişle,
içindeki her
noktası için,
uzayında bulunan fonksiyonların
noktasında değerlendirilmesi sürekli doğrusal operatör olur. O zaman, kullanılarak bu doğrusal operatör
'deki bir elemanla iç çarpım halinde yazılabilir:
Bergman çekirdeği 




Başka bir deyişle, 

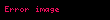


Özel bölgelerde Bergman çekirdeği
Bergman çekirdeği, karmaşık sayılar düzlemdeki bazı özel bölgelerde açık bir şekilde bilinmektedir.
- Birim disk:
ise, o zaman

- (Gerçel kısmı pozitif olan) :
ise, o zaman
Kaynakça
- ^ Elliott, Sam J.; Wynn, Andrew (2011), "Composition Operators on the Weighted Bergman Spaces of the Half-Plane", Proceedings of the Edinburgh Mathematical Society, 54 (2), ss. 374-379, arXiv:0910.0408 $2, doi:10.1017/S0013091509001412, 6 Mart 2016 tarihinde kaynağından arşivlendi, erişim tarihi: 30 Ağustos 2024
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alani olan cok degiskenli kompleks analizde Bergman cekirdegi karesi integrallenebilir holomorf fonksiyonlardan olusan Hilbert uzayinin yani Bergman uzayinin doguran cekirdegidir Stefan Bergman in ardindan isimlendirilmistir TanimCn displaystyle mathbb C n deki bir D displaystyle D bolgesinde karesi integrallenebilir fonksiyonlari L2 D displaystyle L 2 D ile gosterelim Ayrica D displaystyle D bolgesinde tanimli olan holomorf fonksiyonlarin uzayini da H D displaystyle H D ile gosterelim O zaman Bergman uzayi L2 h D L2 D H D displaystyle L 2 h D L 2 D cap H D karesi integrallenebilir holomorf fonksiyonlarin uzayi olacaktir ve su ozelliklere sahiptir L2 h D displaystyle L 2 h D Hilbert uzayidir Oncelikle Bergman uzayi tanimi geregi yine bir Hilbert uzayi olan L2 D displaystyle L 2 D nin dogrusal bir altuzayidir Ayni zamanda Bergman uzayi L2 D displaystyle L 2 D icinde kapalidir Bu yuzden kendi basina da tam bir metrik uzaydir Bu uzayin kapali olmasinin sebebi D displaystyle D nin her tikiz alt kumesi icin supz K f z CK f L2 D displaystyle sup z in K f z leq C K f L 2 D esitsizliginin saglanmasidir Bu halde bir holomorf fonksiyon dizisinin L2 D displaystyle L 2 D icindeki yakinsakligi tikiz kumeler uzerindeki duzgun yakinsakliga yani donusur Boylelikle bu dizinin limiti de holomorf olur L2 D displaystyle L 2 D zaten tam oldugu icin limitin kare integrallenebilir oldugu bilinmektedir O yuzden limit fonksiyonu da L2 h D displaystyle L 2 h D icindedir Yukarida bahsedilen supz K f z CK f L2 D displaystyle sup z in K f z leq C K f L 2 D esitsizliginin D displaystyle D nin her tikiz altkumesinde saglanmasi ayni zamanda D displaystyle D icindeki her z displaystyle z noktasi icin evz f f z displaystyle ev z f mapsto f z gonderiminin bir surekli dogrusal operator oldugunu da gosterir Bir baska deyisle D displaystyle D icindeki her z displaystyle z noktasi icin L2 h D displaystyle L 2 h D uzayinda bulunan fonksiyonlarin z displaystyle z noktasinda degerlendirilmesi surekli dogrusal operator olur O zaman kullanilarak bu dogrusal operator L2 h D displaystyle L 2 h D deki bir elemanla ic carpim halinde yazilabilir evz f Df z hz z dm z displaystyle operatorname ev z f int D f zeta overline eta z zeta d mu zeta dd Bergman cekirdegi K displaystyle K K z z hz z displaystyle K z zeta overline eta z zeta olarak tanimlanir Bergman cekirdegi K z z displaystyle K z zeta z displaystyle z degiskeninde holomorf ve z displaystyle zeta degiskeninde ise tersholomorftur Ayni zamanda asagidaki esitligi saglar f z DK z z f z dm z displaystyle f z int D K z zeta f zeta d mu zeta Baska bir deyisle D displaystyle D icindeki her z displaystyle z noktasi icin L2 h D displaystyle L 2 h D icindeki her holomorf fonksiyonun bu cekirdekle carpilip integralinin alinmasi fonksiyonun z displaystyle z noktasinda degerlendirmesini geri verir z displaystyle z noktasi herhangi bir nokta olabilecegi icin fonksiyon cekirdek tarafindan tekraradan uretilmis olur yani cekirdek uretec gorevi gormektedir Ozel bolgelerde Bergman cekirdegiBergman cekirdegi karmasik sayilar duzlemdeki bazi ozel bolgelerde acik bir sekilde bilinmektedir Birim disk D D 0 1 z C z lt 1 displaystyle D mathbb D 0 1 z in mathbb C vert z vert lt 1 ise o zaman K z z 1p1 1 zz 2 z D displaystyle K z zeta frac 1 pi frac 1 1 z bar zeta 2 zeta in mathbb D Gercel kismi pozitif olan D C z C Rez gt 0 displaystyle D mathbb C z in mathbb C vert Rez gt 0 ise o zamanK z z 1 z z 2 z C displaystyle K z zeta frac 1 overline z zeta 2 zeta in mathbb C Kaynakca Elliott Sam J Wynn Andrew 2011 Composition Operators on the Weighted Bergman Spaces of the Half Plane Proceedings of the Edinburgh Mathematical Society 54 2 ss 374 379 arXiv 0910 0408 2 doi 10 1017 S0013091509001412 6 Mart 2016 tarihinde kaynagindan arsivlendi erisim tarihi 30 Agustos 2024 Ayrica bakinizBergman uzayi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans






