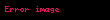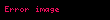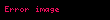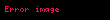Bessel polinomları

Bessel polinomları, matematikteki ortogonal polinomların bir dizisidir. Bessel polinomlarıyla ilgili birbirinden farklı ama birbiriyle yakından ilişkili çok sayıda tanım vardır. Matematikçiler tarafından tercih edilen tanım şu seriyle verilmektedir:^:101

${\displaystyle y_{n}(x)=\sum _{k=0}^{n}{\frac {(n+k)!}{(n-k)!k!}}\,\left({\frac {x}{2}}\right)^{k}.}$

Elektrik mühendisleri tarafından tercih edilen başka bir tanım bazen ters Bessel polinomları olarak bilinir.^:8:15

${\displaystyle \theta _{n}(x)=x^{n}\,y_{n}(1/x)=\sum _{k=0}^{n}{\frac {(n+k)!}{(n-k)!k!}}\,{\frac {x^{n-k}}{2^{k}}}.}$

İkinci tanımın katsayıları birinciyle aynıdır ancak ters sıradadır. Örneğin üçüncü derece Bessel polinomu;

${\displaystyle y_{3}(x)=15x^{3}+15x^{2}+6x+1}$

üçüncü derece ters Bessel polinomu ise;

${\displaystyle \theta _{3}(x)=x^{3}+6x^{2}+15x+15.}$

Bessel elektronik filtrelerinin tasarımında ters Bessel polinomu kullanılmaktadır.

Polinomların özellikleri

Bessel fonksiyonları açısından tanım

Bessel polinomu, polinomun adını aldığı Bessel fonksiyonları kullanılarak da tanımlanabilir.

${\displaystyle y_{n}(x)=\,x^{n}\theta _{n}(1/x)\,}$

${\displaystyle y_{n}(x)={\sqrt {\frac {2}{\pi x}}}\,e^{1/x}K_{n+{\frac {1}{2}}}(1/x)}$

${\displaystyle \theta _{n}(x)={\sqrt {\frac {2}{\pi }}}\,x^{n+1/2}e^{x}K_{n+{\frac {1}{2}}}(x)}$

burada K_n (x) ikinci türden değiştirilmiş bir Bessel fonksiyonudur, y_n(x) sıradan bir polinomdur ve θ_n (x) ters polinomdur.^:7,34Örneğin:

${\displaystyle y_{3}(x)=15x^{3}+15x^{2}+6x+1={\sqrt {\frac {2}{\pi x}}}\,e^{1/x}K_{3+{\frac {1}{2}}}(1/x)}$

Hipergeometrik fonksiyon olarak tanım

Bessel polinomu aynı zamanda birleşik hipergeometrik fonksiyon olarak da tanımlanabilir.^:8

${\displaystyle y_{n}(x)=\,_{2}F_{0}(-n,n+1;;-x/2)=\left({\frac {2}{x}}\right)^{-n}U\left(-n,-2n,{\frac {2}{x}}\right)=\left({\frac {2}{x}}\right)^{n+1}U\left(n+1,2n+2,{\frac {2}{x}}\right).}$

Benzer bir ifade genelleştirilmiş Bessel polinomları için de geçerlidir (aşağıya bakınız):^:35

${\displaystyle y_{n}(x;a,b)=\,_{2}F_{0}(-n,n+a-1;;-x/b)=\left({\frac {b}{x}}\right)^{n+a-1}U\left(n+a-1,2n+a,{\frac {b}{x}}\right).}$

Ters Bessel polinomu genelleştirilmiş bir Laguerre polinomu olarak tanımlanabilir:

${\displaystyle \theta _{n}(x)={\frac {n!}{(-2)^{n}}}\,L_{n}^{-2n-1}(2x)}$

buradan hipergeometrik bir fonksiyon olarak da tanımlanabileceği sonucu çıkar:

${\displaystyle \theta _{n}(x)={\frac {(-2n)_{n}}{(-2)^{n}}}\,\,_{1}F_{1}(-n;-2n;2x)}$

burada (− 2n)_n Pochhammer sembolüdür (yükselen faktöriyel).

Oluşturma işlevi

İndeks kaydırılmış Bessel polinomları üretme işlevine sahiptir;

${\displaystyle \sum _{n=0}^{\infty }{\sqrt {\frac {2}{\pi }}}x^{n+{\frac {1}{2}}}e^{x}K_{n-{\frac {1}{2}}}(x){\frac {t^{n}}{n!}}=1+x\sum _{n=1}^{\infty }\theta _{n-1}(x){\frac {t^{n}}{n!}}=e^{x(1-{\sqrt {1-2t}})}.}$

Göre farklılaşan ${\displaystyle t}$, iptal etme ${\displaystyle x}$, polinomlar için üretme fonksiyonunu verir ${\displaystyle \{\theta _{n}\}_{n\geq 0}}$.

${\displaystyle \sum _{n=0}^{\infty }\theta _{n}(x){\frac {t^{n}}{n!}}={\frac {1}{\sqrt {1-2t}}}e^{x(1-{\sqrt {1-2t}})}.}$

Benzer üretme fonksiyonu ve (𝑦𝑛 polinomlar da) aşağıdakiler için de mevcuttur:

${\displaystyle \sum _{n=0}^{\infty }y_{n-1}(x){\frac {t^{n}}{n!}}=\exp \left({\frac {1-{\sqrt {1-2xt}}}{x}}\right).}$

Ayarlamanın ardından ${\displaystyle t=z-xz^{2}/2}$ üstel fonksiyon için aşağıdaki gösterime sahiptir:^:107

${\displaystyle e^{z}=\sum _{n=0}^{\infty }y_{n-1}(x){\frac {(z-xz^{2}/2)^{n}}{n!}}.}$

Özyineleme

Bessel polinomu aynı zamanda bir yineleme formülüyle de tanımlanabilir:

${\displaystyle y_{0}(x)=1\,}$

${\displaystyle y_{1}(x)=x+1\,}$

${\displaystyle y_{n}(x)=(2n\!-\!1)x\,y_{n-1}(x)+y_{n-2}(x)\,}$

ve

${\displaystyle \theta _{0}(x)=1\,}$

${\displaystyle \theta _{1}(x)=x+1\,}$

${\displaystyle \theta _{n}(x)=(2n\!-\!1)\theta _{n-1}(x)+x^{2}\theta _{n-2}(x)\,}$

Diferansiyel denklem

Bessel polinomu aşağıdaki diferansiyel denkleme uyar:

${\displaystyle x^{2}{\frac {d^{2}y_{n}(x)}{dx^{2}}}+2(x\!+\!1){\frac {dy_{n}(x)}{dx}}-n(n+1)y_{n}(x)=0}$

ve

${\displaystyle x{\frac {d^{2}\theta _{n}(x)}{dx^{2}}}-2(x\!+\!n){\frac {d\theta _{n}(x)}{dx}}+2n\,\theta _{n}(x)=0}$

Diklik

Bessel polinomları ağırlığa göre diktir ${\displaystyle e^{-2/x}}$ karmaşık düzlemin birim çemberi üzerine entegre edilmiştir.^:104 Başka bir deyişle, eğer ${\displaystyle n\neq m}$ ise;

${\displaystyle \int _{0}^{2\pi }y_{n}\left(e^{i\theta }\right)y_{m}\left(e^{i\theta }\right)ie^{i\theta }\mathrm {d} \theta =0}$

Genelleme

Açık Form

Bessel polinomlarının literatürde aşağıdaki gibi bir genellemesi önerilmiştir:

${\displaystyle y_{n}(x;\alpha ,\beta ):=(-1)^{n}n!\left({\frac {x}{\beta }}\right)^{n}L_{n}^{(-1-2n-\alpha )}\left({\frac {\beta }{x}}\right),}$

karşılık gelen ters polinomlar

${\displaystyle \theta _{n}(x;\alpha ,\beta ):={\frac {n!}{(-\beta )^{n}}}L_{n}^{(-1-2n-\alpha )}(\beta x)=x^{n}y_{n}\left({\frac {1}{x}};\alpha ,\beta \right).}$

Açık katsayılar ${\displaystyle y_{n}(x;\alpha ,\beta )}$ polinomlar şunlardır:^:108

${\displaystyle y_{n}(x;\alpha ,\beta )=\sum _{k=0}^{n}{\binom {n}{k}}(n+k+\alpha -2)^{\underline {k}}\left({\frac {x}{\beta }}\right)^{k}.}$

Sonuç olarak, ${\displaystyle \theta _{n}(x;\alpha ,\beta )}$ polinomlar açıkça şu şekilde yazılabilir:

${\displaystyle \theta _{n}(x;\alpha ,\beta )=\sum _{k=0}^{n}{\binom {n}{k}}(2n-k+\alpha -2)^{\underline {n-k}}{\frac {x^{k}}{\beta ^{n-k}}}.}$

Ağırlıklandırma fonksiyonu için;

${\displaystyle \rho (x;\alpha ,\beta ):=\,_{1}F_{1}\left(1,\alpha -1,-{\frac {\beta }{x}}\right)}$

ilişki için diktirler;

${\displaystyle 0=\oint _{c}\rho (x;\alpha ,\beta )y_{n}(x;\alpha ,\beta )y_{m}(x;\alpha ,\beta )\mathrm {d} x}$

m ≠ n ve c için 0 noktasını çevreleyen bir eğri vardır.

α = β = 2, Bessel polinomları üzerinde özelleşir; bu durumda ρ(x) = exp(− 2 / x) olur.

Bessel polinomları için Rodrigues formülü

Yukarıdaki diferansiyel denklemin özel çözümleri olarak Bessel polinomları için Rodrigues formülü şu şekildedir :

${\displaystyle B_{n}^{(\alpha ,\beta )}(x)={\frac {a_{n}^{(\alpha ,\beta )}}{x^{\alpha }e^{-{\frac {\beta }{x}}}}}\left({\frac {d}{dx}}\right)^{n}(x^{\alpha +2n}e^{-{\frac {\beta }{x}}})}$

bu durumda a (α, β)n normalleştirme katsayılarıdır.

İlişkili Bessel polinomları

Bu genellemeye göre ilişkili Bessel polinomları için aşağıdaki genelleştirilmiş diferansiyel denkleme sahibiz:

${\displaystyle x^{2}{\frac {d^{2}B_{n,m}^{(\alpha ,\beta )}(x)}{dx^{2}}}+[(\alpha +2)x+\beta ]{\frac {dB_{n,m}^{(\alpha ,\beta )}(x)}{dx}}-\left[n(\alpha +n+1)+{\frac {m\beta }{x}}\right]B_{n,m}^{(\alpha ,\beta )}(x)=0}$

Böylece ${\displaystyle 0\leq m\leq n}$ . Çözümler şunlardır:

${\displaystyle B_{n,m}^{(\alpha ,\beta )}(x)={\frac {a_{n,m}^{(\alpha ,\beta )}}{x^{\alpha +m}e^{-{\frac {\beta }{x}}}}}\left({\frac {d}{dx}}\right)^{n-m}(x^{\alpha +2n}e^{-{\frac {\beta }{x}}})}$

Sıfırlar

Eğer biri sıfırları gösteriyorsa ${\displaystyle y_{n}(x;\alpha ,\beta )}$ gibi ${\displaystyle \alpha _{k}^{(n)}(\alpha ,\beta )}$ ve ${\displaystyle \theta _{n}(x;\alpha ,\beta )}$ ile ${\displaystyle \beta _{k}^{(n)}(\alpha ,\beta )}$, bu durumda aşağıdaki tahminler mevcuttur:^:82

${\displaystyle {\frac {2}{n(n+\alpha -1)}}\leq \alpha _{k}^{(n)}(\alpha ,2)\leq {\frac {2}{n+\alpha -1}},}$

ve

${\displaystyle {\frac {n+\alpha -1}{2}}\leq \beta _{k}^{(n)}(\alpha ,2)\leq {\frac {n(n+\alpha -1)}{2}},}$

hepsi için ${\displaystyle \alpha \geq 2}$ . Üstelik bu sıfırların hepsinin negatif reel kısmı vardır.

Polinomların sıfırlarının tahminleriyle ilgili daha güçlü teoremlere (daha somut olarak Saff ve Varga'nın Parabol Teoremi veya diferansiyel denklem teknikleri) başvurulursa daha keskin sonuçlar söylenebilir.^:88 Sonuçlardan biri şudur:

${\displaystyle {\frac {2}{2n+\alpha -{\frac {2}{3}}}}\leq \alpha _{k}^{(n)}(\alpha ,2)\leq {\frac {2}{n+\alpha -1}}.}$

Özel değerler

Bessel polinomları ${\displaystyle y_{n}(x)}$ kadar ${\displaystyle n=5}$ olduğuna göre;

${\displaystyle {\begin{aligned}y_{0}(x)&=1\\y_{1}(x)&=x+1\\y_{2}(x)&=3x^{2}+3x+1\\y_{3}(x)&=15x^{3}+15x^{2}+6x+1\\y_{4}(x)&=105x^{4}+105x^{3}+45x^{2}+10x+1\\y_{5}(x)&=945x^{5}+945x^{4}+420x^{3}+105x^{2}+15x+1\end{aligned}}}$

Hiçbir Bessel polinomu, rasyonel katsayılara sahip daha düşük dereceli polinomlara dahil edilemez. Ters Bessel polinomları, katsayıların ters çevrilmesiyle elde edilir. Eşdeğer olarak, ${\textstyle \theta _{k}(x)=x^{k}y_{k}(1/x)}$'dir. Bunun sonucunda aşağıdakiler ortaya çıkmaktadır:

${\displaystyle {\begin{aligned}\theta _{0}(x)&=1\\\theta _{1}(x)&=x+1\\\theta _{2}(x)&=x^{2}+3x+3\\\theta _{3}(x)&=x^{3}+6x^{2}+15x+15\\\theta _{4}(x)&=x^{4}+10x^{3}+45x^{2}+105x+105\\\theta _{5}(x)&=x^{5}+15x^{4}+105x^{3}+420x^{2}+945x+945\\\end{aligned}}}$

Kaynakça

1. ^ ^{a b c d} H. L. Krall ve O. Frink (1948). "A New Class of Orthogonal Polynomials: The Bessel Polynomials". Trans. Amer. Math. Soc. 65 (1): 100-115. doi:10.2307/1990516. 
2. ^ ^{a b c d e} Grosswald, E. (1978). Bessel Polynomials (Lecture Notes in Mathematics). New York: Springer. ISBN . 
3. ^ Christian Berg ve Christope Vignat (2008). "Linearization coefficients of Bessel polynomials and properties of Student-t distributions" (PDF). Constructive Approximation. 27: 15-32. doi:10.1007/s00365-006-0643-6. 23 Ekim 2013 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 16 Ağustos 2006. 
4. ^ "Wolfram Alpha example". 8 Şubat 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Ekim 2023. 
5. ^ A bot will complete this citation soon. Click here to jump the queue arXiv:[1].
6. ^ Saff, E. B.; Varga, R. S. (1976). "Zero-free parabolic regions for sequences of polynomials". SIAM J. Math. Anal. 7 (3): 344-357. doi:10.1137/0507028. 
7. ^ de Bruin, M. G.; Saff, E. B.; Varga, R. S. (1981). "On the zeros of generalized Bessel polynomials. I". Indag. Math. 84 (1): 1-13. 
8. ^ "Sloane's A001498 ", The . OEIS Foundation.
9. ^ Michael Filaseta ve Ognian Trifinov (Ağustos 2, 2002). "The Irreducibility of the Bessel Polynomials". Journal für die Reine und Angewandte Mathematik. 2002 (550): 125-140. doi:10.1515/crll.2002.069.