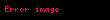Laguerre polinomları, matematikte adını 'den (1834 – 1886) almıştır. Kanonik (benzer) adlandırma Laguerre denklemi'dir:

İkinci mertebeden bir 'dir. Bu denklemin tekil olmayan çözümleri yalnızca n negatif olmayan tam sayı ise vardır. Laguerre polinomlarının sayısal integral hesaplaması için kullanılan formudur
L0, L1, ..., şeklindeki bu polinomları, tanımlayabilmek için Rodrigues formülü tarafından kullanılmalıdır
Diğer önemli her bir tarafından verilir.
Laguerre polinomlarının dizisi bir 'dir.
Laguerre polinomları kuantum mekaniği'nde tek-elektronlu atomun () Schrödinger denklemi'nin radyal kısmının çözümlemesinde ortaya çıkar.
Laguerre polinomları için Fizikte sıklıkla kullanılan bir tanım, n!, gibi bir faktör tarafından burada kullanılan tanımdır.
İlk birkaç polinom
İlk birkaç Laguerre polinomları:
| n | 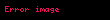 |
| 0 |  |
| 1 | 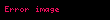 |
| 2 | 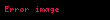 |
| 3 | 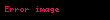 |
| 4 | 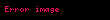 |
| 5 | 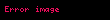 |
| 6 |  |

Tümevarımsal tanım
Tümevarımsal olarak Laguerre polinomları'nın tanımını yapabiliriz, tanımdaki ilk iki polinom:
ve izleyen polinomlar için ile k ≥ 1 'i kullanabiliriz:
Genelleştirilmiş Laguerre polinomları
ortogonal özellikli durumda rastgele değişken ile ise; X ile eşdeğer gösterim
buradan
üstel dağılım sadece gamma dağılımı değildir. önemli Bir polinomal dizi orthogonal olasılık ağırlık fonksiyonunun gama dağılımı için,α > −1,
('Genelleştirilmiş Laguerre polinomu için tanımı ile verilen gama fonksiyonu içeren denklemi görebiliriz):
Bazen uyarlanmış Laguerre polinomları olarak adlandırılır;genelleştirilmiş Laguerre polinomlarının α = 0 durumunda düzenlenmiş polinomları Basit Laguerre polinomları:
Genelleştirilmiş Laguerre polinomlarının özellikleri ve açık örnek
- tarafından tanımlanan Laguerre fonksiyonları ve Kummer dönüşümü
- Eğer
bir tam sayı ise the function reduces to bir polinomun derecesi
. alternaif bir ifade
içindeki terimleridir .
- Genelleştirilmiş Laguerre polinomunun derecesi
ise
( tarafından uygulanan Rodrigues' formülü ile eşdeğer eldesi.)
- İlk birkaç genelleştirilmiş Laguerre polinomları:
- ilk terimleri is (−1)n/n! katsayı'sıdır;
merkezindeki değer 'dir.
- hesaplamada kullanılan genelleştirilmiş Laguerre polinomları için açık formülü sağlar, bununla beraber, algoritma sonuçları ' değildir.
izlenen kararlı metod:
function LaguerreL(n, alpha, x) { L1:= 0; LaguerreL:= 1; for i:= 1 to n { L0:= L1; L1:= LaguerreL; LaguerreL:= ((2* i- 1+ alpha- x)* L1- (i- 1+ alpha)* L0)/ i;} return LaguerreL; } - Ln(α) ile n gerçel, kesinlikle pozitif (burada
bir 'dir), bütün
'ı içindedir .
'in büyük değerleri için polinomun asimptotik davranışı
sabit ve
, verilirse,
, and
..
Ayrıca bakınız
- Matematiksel fonksiyonların listesi
- Rodrigues formülü
- Bessel polinomları
- ; bir dalga kılavuzu veya lazer ışını profili içindeki alan yoğunluğunu tanımlamak için Laguerre polinomlarının önemli bir uygulaması.
Notlar
- ^ Abramowitz, p. 506, 13.3.8 29 Eylül 2009 tarihinde Wayback Machine sitesinde .
Kaynakça
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 22 19 Eylül 2009 tarihinde Wayback Machine sitesinde .", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, .
- B Spain, M G Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 10 deals with Laguerre polynomials.
- Eric W. Weisstein, "Laguerre Polynomial 25 Şubat 2010 tarihinde Wayback Machine sitesinde .", From MathWorld – A Wolfram Web Resource.
- George Arfken ve Hans Weber (2000). Mathematical Methods for Physicists. Academic Press. .
- S. S. Bayin (2006), Mathematical Methods in Science and Engineering, Wiley, Chapter 3.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Laguerre polinomlari matematikte adini den 1834 1886 almistir Kanonik benzer adlandirma Laguerre denklemi dir Laguerre polinomu L n x in karmasik renk grafigi n 1 in 9 a bolumu ve x 2 2i den 2 2i ye kadar 4 un kuvveti z olmak uzerexy 1 x y ny 0 displaystyle x y 1 x y n y 0 Ikinci mertebeden bir dir Bu denklemin tekil olmayan cozumleri yalnizca n negatif olmayan tam sayi ise vardir Laguerre polinomlarinin sayisal integral hesaplamasi icin kullanilan formudur 0 f x e xdx displaystyle int 0 infty f x e x dx L0 L1 seklindeki bu polinomlari tanimlayabilmek icin Rodrigues formulu tarafindan kullanilmalidir Ln x exn dndxn e xxn displaystyle L n x frac e x n frac d n dx n left e x x n right Diger onemli her bir tarafindan verilir f g 0 f x g x e xdx displaystyle langle f g rangle int 0 infty f x g x e x dx Laguerre polinomlarinin dizisi bir dir Laguerre polinomlari kuantum mekanigi nde tek elektronlu atomun Schrodinger denklemi nin radyal kisminin cozumlemesinde ortaya cikar Laguerre polinomlari icin Fizikte siklikla kullanilan bir tanim n gibi bir faktor tarafindan burada kullanilan tanimdir Ilk birkac polinomIlk birkac Laguerre polinomlari n Ln x displaystyle L n x 0 1 displaystyle 1 1 x 1 displaystyle x 1 2 12 x2 4x 2 displaystyle scriptstyle frac 1 2 x 2 4x 2 3 16 x3 9x2 18x 6 displaystyle scriptstyle frac 1 6 x 3 9x 2 18x 6 4 124 x4 16x3 72x2 96x 24 displaystyle scriptstyle frac 1 24 x 4 16x 3 72x 2 96x 24 5 1120 x5 25x4 200x3 600x2 600x 120 displaystyle scriptstyle frac 1 120 x 5 25x 4 200x 3 600x 2 600x 120 6 1720 x6 36x5 450x4 2400x3 5400x2 4320x 720 displaystyle scriptstyle frac 1 720 x 6 36x 5 450x 4 2400x 3 5400x 2 4320x 720 ilk alti Laguerre polinomu Tumevarimsal tanimTumevarimsal olarak Laguerre polinomlari nin tanimini yapabiliriz tanimdaki ilk iki polinom L0 x 1 displaystyle L 0 x 1 L1 x 1 x displaystyle L 1 x 1 x ve izleyen polinomlar icin ile k 1 i kullanabiliriz Lk 1 x 1k 1 2k 1 x Lk x kLk 1 x displaystyle L k 1 x frac 1 k 1 left 2k 1 x L k x kL k 1 x right Genellestirilmis Laguerre polinomlariortogonal ozellikli durumda rastgele degisken ile ise X ile esdeger gosterim f x e xif x gt 0 0if x lt 0 displaystyle f x left begin matrix e x amp mbox if x gt 0 0 amp mbox if x lt 0 end matrix right buradan E Ln X Lm X 0 whenever n m displaystyle E left L n X L m X right 0 mbox whenever n neq m ustel dagilim sadece gamma dagilimi degildir onemli Bir polinomal dizi orthogonal olasilik agirlik fonksiyonunun gama dagilimi icin a gt 1 f x xae x G 1 a if x gt 0 0if x lt 0 displaystyle f x left begin matrix x alpha e x Gamma 1 alpha amp mbox if x gt 0 0 amp mbox if x lt 0 end matrix right Genellestirilmis Laguerre polinomu icin tanimi ile verilen gama fonksiyonu iceren denklemi gorebiliriz Ln a x x aexn dndxn e xxn a displaystyle L n alpha x x alpha e x over n d n over dx n left e x x n alpha right Bazen uyarlanmis Laguerre polinomlari olarak adlandirilir genellestirilmis Laguerre polinomlarinin a 0 durumunda duzenlenmis polinomlari Basit Laguerre polinomlari Ln 0 x Ln x displaystyle L n 0 x L n x Genellestirilmis Laguerre polinomlarinin ozellikleri ve acik ornek tarafindan tanimlanan Laguerre fonksiyonlari ve Kummer donusumu Ln a x n an M n a 1 x n an i 0 1 i ni a ii xi displaystyle L n alpha x n alpha choose n M n alpha 1 x n alpha choose n sum i 0 1 i frac n choose i alpha i choose i x i ex n an M a n 1 a 1 x displaystyle e x cdot n alpha choose n M alpha n 1 alpha 1 x exsin np sin n a p L a n 1 a x displaystyle frac e x sin n pi sin n alpha pi L alpha n 1 alpha x ex i 0 1 i a n in xii displaystyle e x cdot sum i 0 1 i alpha n i choose n frac x i i Eger n displaystyle n bir tam sayi ise the function reduces to bir polinomun derecesi n displaystyle n alternaif bir ifade Ln a x 1 nn U n a 1 x displaystyle L n alpha x frac 1 n n U n alpha 1 x icindeki terimleridir Genellestirilmis Laguerre polinomunun derecesi n displaystyle n ise Ln a x i 0n 1 i n an i xii displaystyle L n alpha x sum i 0 n 1 i n alpha choose n i frac x i i tarafindan uygulanan Rodrigues formulu ile esdeger eldesi Ilk birkac genellestirilmis Laguerre polinomlari L0 a x 1 displaystyle L 0 alpha x 1 L1 a x x a 1 displaystyle L 1 alpha x x alpha 1 L2 a x x22 a 2 x a 2 a 1 2 displaystyle L 2 alpha x frac x 2 2 alpha 2 x frac alpha 2 alpha 1 2 L3 a x x36 a 3 x22 a 2 a 3 x2 a 1 a 2 a 3 6 displaystyle L 3 alpha x frac x 3 6 frac alpha 3 x 2 2 frac alpha 2 alpha 3 x 2 frac alpha 1 alpha 2 alpha 3 6 ilk terimleri is 1 n n katsayi sidir Ln a 0 n an naG a 1 displaystyle L n alpha 0 n alpha choose n approx frac n alpha Gamma alpha 1 merkezindeki deger dir hesaplamada kullanilan genellestirilmis Laguerre polinomlari icin acik formulu saglar bununla beraber algoritma sonuclari degildir izlenen kararli metod function LaguerreL n alpha x L1 0 LaguerreL 1 for i 1 to n L0 L1 L1 LaguerreL LaguerreL 2 i 1 alpha x L1 i 1 alpha L0 i return LaguerreL Ln a ile n gercel kesinlikle pozitif burada 1 n iLn i a i 0n displaystyle left 1 n i L n i alpha right i 0 n bir dir butun 0 n a n 1 n a displaystyle 0 n alpha n 1 sqrt n alpha i icindedir n displaystyle n in buyuk degerleri icin polinomun asimptotik davranisi a displaystyle alpha sabit ve x gt 0 displaystyle x gt 0 verilirse Ln a x na2 14pex2xa2 14cos 2x n a 12 p2 a 12 displaystyle L n alpha x approx frac n frac alpha 2 frac 1 4 sqrt pi frac e frac x 2 x frac alpha 2 frac 1 4 cos left 2 sqrt x left n frac alpha 1 2 right frac pi 2 left alpha frac 1 2 right right andLn a x na2 142pe x2xa2 14exp 2x n a 12 displaystyle L n alpha x approx frac n frac alpha 2 frac 1 4 2 sqrt pi frac e frac x 2 x frac alpha 2 frac 1 4 exp left 2 sqrt x left n frac alpha 1 2 right right Ayrica bakinizMatematiksel fonksiyonlarin listesi Rodrigues formulu Bessel polinomlari bir dalga kilavuzu veya lazer isini profili icindeki alan yogunlugunu tanimlamak icin Laguerre polinomlarinin onemli bir uygulamasi Notlar Abramowitz p 506 13 3 8 29 Eylul 2009 tarihinde Wayback Machine sitesinde KaynakcaAbramowitz Milton Stegun Irene A eds 1965 Chapter 22 19 Eylul 2009 tarihinde Wayback Machine sitesinde Handbook of Mathematical Functions with Formulas Graphs and Mathematical Tables New York Dover ISBN 0 486 61272 4 B Spain M G Smith Functions of mathematical physics Van Nostrand Reinhold Company London 1970 Chapter 10 deals with Laguerre polynomials Eric W Weisstein Laguerre Polynomial 25 Subat 2010 tarihinde Wayback Machine sitesinde From MathWorld A Wolfram Web Resource George Arfken ve Hans Weber 2000 Mathematical Methods for Physicists Academic Press ISBN 0 12 059825 6 S S Bayin 2006 Mathematical Methods in Science and Engineering Wiley Chapter 3
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State