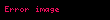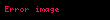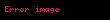Birim küre, belirli merkez noktasından 1 birim uzaklıkta olan noktalar kümesidir.Mesafelerin genellenmiş kavramları olarak da kullanılabilir.Kapalı bir birim küre,merkezden 1 birim az veya 1 birime eşit uzaklıktaki noktalar kümesidir.Genellikle,boşluktaki orijinden bir nokta ayırt edilmişitir ve bu noktanın birim kürenin veya birim topun merkezi olduğu anlaşılır.Bu yüzden birim küre ya da birim topun aynı olduğu söylenir. Örneğin;bir boyutlu küre,genellikle bir halka olarak adlandırılan bir yüzeydir ve çember bir içi yüzeye ve dış yüzeye sahipse iki boyutlu bir küredir.Benzer bir şekilde ,halk dilinde küre olarak bilinen Öklid katısının yüzeyi iki boyutlu küredir ve ayrıca içi ve dış yüzeye sahip olduğunda üç boyutlu küre olur. Bir birim küre basitçe bir küre yarıçapına sahiptir.Birim kürenin önemi ,herhangi bir kürenin ölçeklendirme ve çevirme kombinasyonlarına dönüşebilmesinden anlayabiliriz.Bu yolla,çalışırken kürenin temel özelliklerini daha aza indirgeyebiliriz.

Öklid uzayında birim küre ve toplar
Öklid uzayında n boyutunda,birim küre aşağıdaki denklemi sağlayan noktalar 
Ve kapalı birim top ,aşağıdaki eşitsizliği sağlayan noktalar kümesidir.
Genel alan ve hacim formülleri
Yarıçapı 1 birim olan ve x-, y- ve z- eksenlerinde değişikliğe sahip olmayan elipsoid birim kürenin klasik denklemini verir.
Öklid uzayında n boyutunda bir birim kürenin hacmi ve birim kürenin yüzey alanı birçok önemli formülde karşımıza çıkabilir.n boyutlu bir kürenin hacmini Vn olarak gösteririz,bu gama fonksiyonu kullanarak açıklanabilir.
n!! double faktöriyel demektir. (n-1) boyutlu birim kürenin hiperhacmi (n boyutta bir topun yüzey alanı gibi) An ile gösterilir ve alttaki formülle açıklanabilr;
Son eşitlikte n > 0 olan değerler için kullanılabilr. Bazı 
 |  (yüzey alan) (yüzey alan) |  (hacim) (hacim) | ||
|---|---|---|---|---|
| 0 |  | 0 |  | 1 |
| 1 |  | 2 |  | 2 |
| 2 |  | 6.283 |  | 3.141 |
| 3 |  | 12.57 |  | 4.189 |
| 4 | 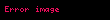 | 19.74 |  | 4.935 |
| 5 |  | 26.32 |  | 5.264 |
| 6 |  | 31.01 |  | 5.168 |
| 7 |  | 33.07 |  | 4.725 |
| 8 |  | 32.47 |  | 4.059 |
| 9 |  | 29.69 |  | 3.299 |
| 10 |  | 25.50 | 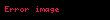 | 2.550 |
n ≥ 2 için genişletilmiş ondalık değerleri hassas olarak yuvarlanır.
Önyineleme
An değerleri tekrarlamayı karşılar,
for
.
Vn değerleri tekrarlamayı karşılar,
for
.
Fonksiyonel boyutlar
An ve Vn herhangi bir gerçek sayın ≥ 0, için hesaplanabilir. n 0 olmayan bir tam sayı olduğunda kürenin alanını veya topun hacmini saklamak için uygun koşullar vardır.


Diğer yarıçapı
Yarıçapı r olan (n–1) boyutlu bir kürenin yüzey alanı An rn−1 ve yarıçapı r olan n boyutlu bir topun hacmi Vn rn. For instance, the area is {{Kayma|A =.Örneğin,yarıçapı r olan üç boyutlu topun yüzey alanı A = 4π r 2’dir.Yarıçapı r olan üç boyutlu bir topun hacmi ise V = 4π r 3 / 3 ‘dir.
Normlu uzaylarda birim topları
Normlu bir uzayda 
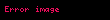
Kapalı birim topun içi; (V,||•||),
Birim küre ayrık ve ortak sınırlara sahip;birim küre (V,||•||),
Birim topun şekli tamamen seçilen norma bağlıdır.İyi köşelere sahip olabilir ve [−1,1] gibi görülebilir ve norm n,durumunda l∞ in Rn.Normal yuvarlak bir top genellikle Hilbert spacenormu üzerinde sonlu-boyutlu Öklid mesafesi üzerinde anlaşılır.Sınırladığı alan birim kürenin genellikle hangi anlama geldiğini tanımlar.p çeşitli değerlerinde,birim topun iki boyutlu uzayı için burada bazı fotoğraflar vardır.(birim top konkav olduğunda p < 1,konveks olduğunda p ≥ 1):

Bu nedenle bu durump ≥ 1 göstermektedir. İki boyutlu birim topların çevreleri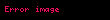
maximum değerdir.
minimum değerdir.
Genellemeler
Metrik uzaylar
Yukarıda tanımlanan her üç doğrudan, seçilen orijine göre bir metrik uzay açıkça genelleştirilebilir.Ancak,topolojik düşünceler(iç,kapatma,sınır) aynı yola (ultrametric alanlarda,açık kapalı kümelerin tümü)başvurmaya ihtiyaç duymaz ve birim küre bazı metrik uzaylarda boş bile olabilir.
Kuadratik formlar
Eğer V gerçek olan bir doğrusal uzayın ’u F:V → R,daha sonra { p ∈ V : F(p) = 1 } birim küre ya da Vnin birim yarı küresidir denebilir.Örneğin;kuadrik formu 
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Birim kure belirli merkez noktasindan 1 birim uzaklikta olan noktalar kumesidir Mesafelerin genellenmis kavramlari olarak da kullanilabilir Kapali bir birim kure merkezden 1 birim az veya 1 birime esit uzakliktaki noktalar kumesidir Genellikle bosluktaki orijinden bir nokta ayirt edilmisitir ve bu noktanin birim kurenin veya birim topun merkezi oldugu anlasilir Bu yuzden birim kure ya da birim topun ayni oldugu soylenir Ornegin bir boyutlu kure genellikle bir halka olarak adlandirilan bir yuzeydir ve cember bir ici yuzeye ve dis yuzeye sahipse iki boyutlu bir kuredir Benzer bir sekilde halk dilinde kure olarak bilinen Oklid katisinin yuzeyi iki boyutlu kuredir ve ayrica ici ve dis yuzeye sahip oldugunda uc boyutlu kure olur Bir birim kure basitce bir kure yaricapina sahiptir Birim kurenin onemi herhangi bir kurenin olceklendirme ve cevirme kombinasyonlarina donusebilmesinden anlayabiliriz Bu yolla calisirken kurenin temel ozelliklerini daha aza indirgeyebiliriz Some 1 spheres x 2 displaystyle boldsymbol x 2 altta birinci bolumde bahsedilen Oklid uzayi icin normlar norm Oklid uzayinda birim kure ve toplarOklid uzayinda n boyutunda birim kure asagidaki denklemi saglayan noktalar x1 xn displaystyle x 1 ldots x n kumesidir x12 x22 xn2 1 displaystyle x 1 2 x 2 2 cdots x n 2 1 Ve kapali birim top asagidaki esitsizligi saglayan noktalar kumesidir x12 x22 xn2 1 displaystyle x 1 2 x 2 2 cdots x n 2 leq 1 Genel alan ve hacim formulleri Yaricapi 1 birim olan ve x y ve z eksenlerinde degisiklige sahip olmayan elipsoid birim kurenin klasik denklemini verir f x y z x2 y2 z2 1 displaystyle f x y z x 2 y 2 z 2 1 Oklid uzayinda n boyutunda bir birim kurenin hacmi ve birim kurenin yuzey alani bircok onemli formulde karsimiza cikabilir n boyutlu bir kurenin hacmini Vn olarak gosteririz bu gama fonksiyonu kullanarak aciklanabilir Vn pn 2G 1 n 2 pn 2 n 2 if n 0 is even p n 2 2 n 2 n if n 0 is odd displaystyle V n frac pi n 2 Gamma 1 n 2 begin cases pi n 2 n 2 amp mathrm if n geq 0 mathrm is even pi lfloor n 2 rfloor 2 lceil n 2 rceil n amp mathrm if n geq 0 mathrm is odd end cases n double faktoriyel demektir n 1 boyutlu birim kurenin hiperhacmi n boyutta bir topun yuzey alani gibi An ile gosterilir ve alttaki formulle aciklanabilr An nVn npn 2G 1 n 2 2pn 2G n 2 displaystyle A n nV n frac n pi n 2 Gamma 1 n 2 frac 2 pi n 2 Gamma n 2 Son esitlikte n gt 0 olan degerler icin kullanilabilr Bazi n displaystyle n degerleri icin bazi yuzey alanlar ve hacimleri n displaystyle n An displaystyle A n yuzey alan Vn displaystyle V n hacim 0 0 1 0 p0 displaystyle 0 1 0 pi 0 0 1 0 p0 displaystyle 1 0 pi 0 11 1 21 1 p0 displaystyle 1 2 1 1 pi 0 2 21 1 p0 displaystyle 2 1 1 pi 0 22 2 1 1 p1 2p displaystyle 2 1 1 pi 1 2 pi 6 283 1 1 p1 p displaystyle 1 1 pi 1 pi 3 1413 3 22 3 p1 4p displaystyle 3 2 2 3 pi 1 4 pi 12 57 22 3 p1 4 3 p displaystyle 2 2 3 pi 1 4 3 pi 4 1894 4 1 2 p2 2p2 displaystyle 4 1 2 pi 2 2 pi 2 19 74 1 2 p2 1 2 p2 displaystyle 1 2 pi 2 1 2 pi 2 4 9355 5 23 5 p2 8 3 p2 displaystyle 5 2 3 5 pi 2 8 3 pi 2 26 32 23 5 p2 8 15 p2 displaystyle 2 3 5 pi 2 8 15 pi 2 5 2646 6 1 3 p3 p3 displaystyle 6 1 3 pi 3 pi 3 31 01 1 3 p3 1 6 p3 displaystyle 1 3 pi 3 1 6 pi 3 5 1687 7 24 7 p3 16 15 p3 displaystyle 7 2 4 7 pi 3 16 15 pi 3 33 07 24 7 p3 16 105 p3 displaystyle 2 4 7 pi 3 16 105 pi 3 4 7258 8 1 4 p4 1 3 p4 displaystyle 8 1 4 pi 4 1 3 pi 4 32 47 1 4 p4 1 24 p4 displaystyle 1 4 pi 4 1 24 pi 4 4 0599 9 25 9 p4 32 105 p4 displaystyle 9 2 5 9 pi 4 32 105 pi 4 29 69 25 9 p4 32 945 p4 displaystyle 2 5 9 pi 4 32 945 pi 4 3 29910 10 1 5 p5 1 12 p5 displaystyle 10 1 5 pi 5 1 12 pi 5 25 50 1 5 p5 1 120 p5 displaystyle 1 5 pi 5 1 120 pi 5 2 550 n 2 icin genisletilmis ondalik degerleri hassas olarak yuvarlanir Onyineleme An degerleri tekrarlamayi karsilar A0 0 displaystyle A 0 0 A1 2 displaystyle A 1 2 A2 2p displaystyle A 2 2 pi An 2pn 2An 2 displaystyle A n frac 2 pi n 2 A n 2 for n gt 2 displaystyle n gt 2 Vn degerleri tekrarlamayi karsilar V0 1 displaystyle V 0 1 V1 2 displaystyle V 1 2 Vn 2pnVn 2 displaystyle V n frac 2 pi n V n 2 for n gt 1 displaystyle n gt 1 Fonksiyonel boyutlar An ve Vn herhangi bir gercek sayin 0 icin hesaplanabilir n 0 olmayan bir tam sayi oldugunda kurenin alanini veya topun hacmini saklamak icin uygun kosullar vardir x 1 boyutlu kurenin hiperhacmini surekli x fonksiyonu olarak gosterir x boyutlu topun yuzey alan gibi grafik x boyutta bir topun hacmini surekli x fonksiyonu olarak gosterir Diger yaricapi Yaricapi r olan n 1 boyutlu bir kurenin yuzey alani An rn 1 ve yaricapi r olan n boyutlu bir topun hacmi Vn rn For instance the area is Kayma A Ornegin yaricapi r olan uc boyutlu topun yuzey alani A 4p r 2 dir Yaricapi r olan uc boyutlu bir topun hacmi ise V 4p r 3 3 dir Normlu uzaylarda birim toplariNormlu bir uzayda V displaystyle V norm la displaystyle cdot birlikte acik birim top asagidaki bagintiyi verir x V x lt 1 displaystyle x in V x lt 1 Kapali birim topun ici V x V x 1 displaystyle x in V x leq 1 Birim kure ayrik ve ortak sinirlara sahip birim kure V x V x 1 displaystyle x in V x 1 Birim topun sekli tamamen secilen norma baglidir Iyi koselere sahip olabilir ve 1 1 gibi gorulebilir ve norm n durumunda l in Rn Normal yuvarlak bir top genellikle Hilbert spacenormu uzerinde sonlu boyutlu Oklid mesafesi uzerinde anlasilir Sinirladigi alan birim kurenin genellikle hangi anlama geldigini tanimlar p cesitli degerlerinde birim topun iki boyutlu uzayi icin burada bazi fotograflar vardir birim top konkav oldugunda p lt 1 konveks oldugunda p 1 Bu nedenle bu durump 1 gostermektedir Iki boyutlu birim toplarin cevreleriCp displaystyle C p C0 C 8 displaystyle C 0 C infty 8 maximum degerdir C1 42 displaystyle C 1 4 sqrt 2 minimum degerdir C2 2p displaystyle C 2 2 pi GenellemelerMetrik uzaylar Yukarida tanimlanan her uc dogrudan secilen orijine gore bir metrik uzay acikca genellestirilebilir Ancak topolojik dusunceler ic kapatma sinir ayni yola ultrametric alanlarda acik kapali kumelerin tumu basvurmaya ihtiyac duymaz ve birim kure bazi metrik uzaylarda bos bile olabilir Kuadratik formlar Eger V gercek olan bir dogrusal uzayin u F V R daha sonra p V F p 1 birim kure ya da Vnin birim yari kuresidir denebilir Ornegin kuadrik formu x2 y2 displaystyle x 2 y 2 birine esit ayarlandiginda bolunmus karmasik sayilar duzleminde birim cember rolunu oynayan birim hiperbol olusturulur Kuadratik formu x2 uzayin icinde birim kure icin bir cizgi cifti olusturur Kaynakca
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State