Bu madde, uygun değildir. (Şubat 2014) |
Bose-Einstein yoğunlaşması (BEY), parçacıkları bozonlardan oluşan maddelerin en alt enerji seviyesinde yoğunlaştığı, kuantum etkilerinin gözlenebildiği maddenin bir halidir. Bozonik atomlar için, seyreltilmiş gaz halinde aracılığıyla mutlak sıfır sıcaklığına doğru inilerek (0 K veya -273,15 °C ye çok yakın) bu hale geçiş yani yoğunlaşma sağlanabilir. Atomların klasik gazlardan farklı olarak Maxwell-Boltzmann istatistiği yerine makroskobik olarak/büyük ölçekte uyması BEY'nin belirleyici özelliğidir.

Daha sonra yapılan deneylerin karmaşık etkileşimler ortaya çıkarmasına rağmen, maddenin bu hali ilk olarak Satyendra Nath Bose ve Albert Einstein tarafından 1924-1925 yıllarında genel olarak tahmin edildi. Bose ilk olarak Einstein'a "ışık kuanta"sının (artık foton olarak adlandırılıyor) kuantum istatistiğiyle ilgili bir makale yollamıştır. Einstein bundan etkilenir ve makaleyi İngilizce'den Almanca'ya çevirerek Zeitschrift für Physik Bose için sunar ve makale yayımlanır. (Einstein'in baskı metni bir ara kaybolduğunun düşünülmesine rağmen Leiden Üniversitesinde 2005 yılında bulunur). Einstein daha sonra iki farklı makalede Bose 'un fikirlerini madde parçacıkları konusuna genişletir. Bose ve Einstein in çalışmaları sonucunda birbiriyle eş parçacıkların tam fırıllarının istatistiksel dağılımını tanımlayan (şimdilerde bozon olarak adlandırılan) Bose-Einstein istatistiği ile yönetilen Bose gazı kavramı ortaya çıkmıştır. . Einstein bozonik atomlarının çok düşük derecelere kadar soğumasının yeni bir madde formu oluşturarak ulaşılabilir en düşük kuantum durgusuna dönüştüğünü göstermiştir. 1938 yılında Fritz London BEC yi 4He un üstün akışkanlık ve üstün iletkenlik mekanizmasıyla tasarladı. 1995 yılında, ilk gaz yoğunlaşması Eric Cornell ve Carl Wieman tarafından University of Colorado ar Boulder NIST-JILA laboratuvarında rubidyum atomu gazlarının 170 nanokelvin (nK)'e (1.7×10−7 K) soğutulmasıyla üretilmiştir. Bu başarılarıyla Cornell, Wieman ve Wolfgang Ketterle MIT'de 2001 Nobel Fizik Ödülünü almıştır. Kasım 2010 da ilk BEC fotonu gözlemlenmiştir. 2012 de ise BEC foton teorisi geliştirilmiştir [9][10]. [9][10] Bu BEC ye geçiş belirgin içsel serbestlik derecesi ile etkileşmeyen parçacıklar içeren üç boyutlu üniform gazların kritik sıcaklığın altında oluşur:
-
kritik sıcaklık, , bozon başına düşen kütle, indirgenmiş Planck sabiti, Boltzmann sabiti Riemann zeta fonksiyonu;
Einstein’ ın argümanı
N tane her biri iki kuantum durgusundan birinde olanveetkileşmeyen parçacıklardan oluşan bir koleksiyon düşünün. Eğer bu iki hal enerjice eşitse, her farklı yapılandırma eşit şanslıdır. Eğer her parçacıkların hangi parçacık olduğunu bilirsek ve eğer her parçacık bağımsız olarak ya da içinde olursa tane farklı yapılandırma olur. Neredeyse her yapılandırmalarında, parçacıkların yaklaşık yarısı , diğer yarısı kapsamındadır. Dengesi ise istatistiksel bir etkidir: parçacıklar eşit dağıldığında yapılandırma en büyüktür. Eğer parçacıklar birbirinden ayırt edilemezse sadece N+1 yapılandırma olur. K tane parçacığın halinde tane parçacık halinde olur. Partiküllerin ya da halinde olması ayırt edilemese de her Kdeğeri tüm sistemin kuantum durgusunu belirler. Tüm durumların eşit şanslı olduğu durumlarda istatistiksel bir dağılma olmaz. Bu durum sadece tüm parçacıkların yarı yarıya dağılırken tüm parçacıkların halinde olması kadar muhtemeldir. Ayırt edilebilir durumda, daha büyük N sayıları için, halindeki kısım hesaplanabilir. Bu durum tamamen bir bozuk paranın tura gelme olasılığı olan p = exp(−E/T) kadardır. Yazı gelme olasılığı ise p nin ve enerjinin olan denklemine eşittir. Ayırt edilemez durumlarda, her K kendi ayrı Boltzman olasılığına sahip tek haldedir. Bu yüzden dağılım olasılığı üslüdür:
Daha büyük N değerleri için C normalleştirme sabiti . Beklenilen toplam parçacık sayıları en düşük enerji durumunda değildir eğer limit iken e eşittir. Bu durum N sayısı büyükken değil sadece sabit değere ulaştığı durumda gelişir. Bu parçacıkların toplam sayısının ihmal edilebilir kısmındadır. Bu yüzden, termal dengede olan yeterli sayıdaki Boz parçacıklar çoğunlukla temel durumdadır. Enerji değişimi çok küçük olsa bile sadece çok az parçacık uyarılmış durumdadır. Olarak isimlendirilen değişik bir momentum durumunda olan bir gaz parçacığı düşünelim. Eğer yüksek ve düşük yoğunluklar için parçacıkların toplam sayısı termal olarak ulaşılabilir parçacıkların sayısından az ise her bir parçacık ayrı bir halde olacaktır. Bu limitler içerisinde gaz klasiktir. Yoğunluk arttığında ya da sıcaklık düştüğünde, parçacık başına düşen ulaşılabilir durum küçülür. Bu noktada, izin verilen istatistiksel ağırlıktan daha çok parçacık tek duruma geçmek için zorlanacaktır. Bu noktadan sonra herhangi ekstra parçacık temel seviyeye eklenecektir. Herhangi bir yoğunlukta, bütünlemede, tüm momentum durumlarının üzerinde değişim sıcaklığını hesaplamak için, maksimum sayıdaki uyarılmış parçacıklar, :
Tümlev kB ve ℏ faktörleri ile değerlendirilir ve boyutlu analizlerle yenileştirilirse, ilerleyen kısımlarda kritik sıcaklık formülünü verecektir. Bu yüzden bu tümlev kritik sıcaklık ve ihmal edilen kimyasal potansiyele karşılık gelen parçacık sayılarını tanımlar. Bose-Einstein istatistiksel dağılımında μ hala BEC nin sıfır olmayan fakat temel durum enerjisinden düşüktür. Özellikle temel durumdan bahsetmek dışında, μ çoğunluk enerji ve momentum durumuna yaklaştırılır, as μ ≈ 0. daki gibi. Gross-Pitaevskii Denklemi Ana makale: Gross-Pitaevskii denklemi BEC nin bu durumu yoğuşuk un dalga denklemi ile tanımlanır. Bu yapıdaki bir sistemde parçacık yoğunluğu olarak yorumlanır. Bu yüzden toplam atomların sayısı dır. Sağlanan tüm gerekli atomlar yoğuşuk iken (temel seviyeye yoğuşan), bozonlar ana alan teorisini tehdit ederler. Durumu ile alakalı enerji (E) ise:
- dir.
iken sonsuz derecede küçük değişimleri baz alan enerjiyi küçültmek ve atom sayılarını sabit tutmak Gross-Pitaevskii denklemini (GPE) ortaya çıkarır (lineer olmayan Schrödinger denklemi olarak da bilinir):
-
bozonların kütlesi, dış potensiyeli, parçacık arası etkileşimleri
GPE, BEC lerin davranışları ile ilgili iyi tanımlar ortaya koyar ve bu yüzden teorik analizlerde kullanılır.
Gross-Pitaevskii haricindeki modeller
BEC’nin Gross-Pitaeyskii modeli BEC’nin belirli sınıfları için geçerli olan fiziksel bir yaklaşımdır. Yapı itibarıyla, GPE şu basitleştirmeyi kullanmaktadır: GPE, yoğun parçacıklar arasındaki etkileşimlerin iki “body” tipinden kaynaklandığını farz eder ve serbest enerjinin büyük katkısını yok sayar. Bu varsayımlar genellikle seyreltilmiş 3 boyutlu yoğuşuklar için uygundur. Eğer bu varsayımlardan biri olmazsa, yoğuşuk dalga fonksiyonu (wavefunction) yüksek dereceli terimler içerir. Hatta bazı fiziksel sistemler için terim miktarı sonsuza kadar gider ve denklem polinom olmaz. Bu durumun meydana geldiği örnekler: Bose-Fermi birleşik yoğuşuklar, etkili düşük boyutlu yoğuşuklar, yoğun yoğuşuklar ve süper akışkan/süper sıvı (mutlak sıfırın bir derece üstündeki sıvı hali) kabuklar ve damlacıklar. Keşif 1938 yılında, Pyotr Kapitsa, John Allen ve Don Misener, süper akışkan olarak bilinen ve 2.17 Kelvin’den düşük sıcaklıktaki helium-4’ü keşfettiler. Süper akışkan helium, sıfır adalılık ve sayısal girdap (quantized vortices) gibi olağan dışı birçok özellik içerir. Öncelikle, süper akışkanlığın sıvının kısmi Bose-Einstein yoğunluğundan dolayı olduğuna inanıldı. Aslında süper akışkan helyumun çoğu özelliği Cornell, Wieman ve Ketterle tarafından oluşturulan gazlı Bose-Einstein yoğuşuklarında görülmektedir. Süper akışkan helium-4 gazdan ziyade sıvıdır. Yani atomlar arasındaki etkileşimler göreceli olarak güçlüdür: Bose-Einstein’ının yoğunlaşma teorisi Süper akışkan helium-4’ü tanımlamak için ciddi şekilde değiştirilmelidir. Ayrıca bozon yerine fermiyum içeren helium-3, düşük sıcaklıkta süper akışkan hale geçer. Bu durum 2 atomlu bozonik “Cooper çifti” biçimlenme ile açıklanabilir. İlk saf Bose-Einstein yoğuşuğu 5 Haziran 1995 yılında Eric Cornell, Carl Wieman ve JILA daki meslektaşları tarafından oluşturuldu. Bu çalışmayı lazer soğutucu ve manyetik buharlaşmalı soğutucu kullanarak, 170 NK dan düşük yaklaşık 2 bin rubidiım-87 atomu içeren seyreltilmiş buharı soğutarak yapmışlardır. 4 ay sonra MİT’ten Wolfgang Ketterle sodium-23'ten yapılmış bir yoğuşkanı oluşturdu. Ketterle’nin yoğuşkanı yaklaşık 100 kat daha fazla atom içerir. Bu durum ona 2 farklı yoğunlaşma arasında kuantum mekanik etkileşiminin gözlemlenmesi gibi önemli sonuçlar sağlar. Cornell, Wieman ve Ketterle başarıları için 2001 yılında Nobel Fizik Ödülü’nü kazanmışlardır. JILA çalışmasından bir ay sonra Rice Üniversitesinde, Randall Hulet önderliğindeki bir grup Lithium atomlarının yoğuşuğu oluşturduklarını duyurmuşlardır. Lithium, yoğuşuğu duraksız olmasına ve atomların çarpışmasına neden olan ilginç etkileşimler göstermektedir. Hulet ve meslektaşları, bir sonraki denemede yoğuşuğu yaklaşık 1000 atoma kadar kuantum basıncı ile dengelenebileceğini göstermiştir. Bose-Einstein yoğunlaşması ayrıca katılarda sanki parçacıklara uygulanabilir. Antiferromagnetteki bir magnon “dönme 1” taşır ve Bose-Einstein statiğine uyar. Magnonların yoğunlukları, dış manyetik alanı tarafından kontrol edilir. Bu teknik, Bose sıvısıyla güçlü bir etkileşime giren seyreltilmiş Bose gazından geniş aralıkta bozon yoğunluklarına ulaşabilmeyi sağlar. Yoğunlaşma noktasında gözlemlenen manyetik sıralanma süper akışkanlık analoğudur. 1999 da magnonların Bose yoğunlaşması antiferromagnet Tl Cu Cl3 içerisinde gösterilmiştir. Yoğunlaşma 14 K kadar yüksek sıcaklıklarda gözlenmiştir. Yüksek sıcaklığa geçişin nedeni magnonların daha yüksek yoğunlukta ve daha küçük kütlede olmasıdır. 2006 yılında, ferromagnetlerdeki magnonların yoğunlaşması oda sıcaklığında gösterilmiştir.
Hız Dağılımı Grafiği
Bu makaleye eşlik eden figürde, hız dağılım bilgisi gaz halindeki rubidyum atomlarının Bose-Einstein yoğuşuğu oluşturmasını işaret eder. Sahte renkler her hızdaki atomların sayılarını belirtir (kırmızı en az sayıda, beyaz en çok sayıda). Beyaz ve açık mavi renkleriyle görülen alanlar en düşük hızları temsil eder. Zirve Heisenberg belirsizlik prensibinden dolayı sonsuz değildir; Atomlar boşlukta belirli bir alanda sıkışmadığı sürece hız dağılımları belirli bir minimum genişliktedir. Bu genişlik manyetik sıkışma potansiyelin eğriliği tarafından belirlenir. Daha sıkıca kapatılmış yönler daha büyük genişlikte hız dağılımlarına sahiptir. Bu anizotropinin sağdaki zirvesi saf kuantum-mekaniği etkisidir ve soldaki normal dağılımda bulunmaz. Bu grafik 1999 da Ralph Baierlein tarafından yazılan Thermal Physics [24] kitabının kapağında kullanılmıştır.
Girdaplar
Birçok sistemde olduğu gibi, BEC’lerde de bazı girdaplar bulunmaktadır. Bu girdaplar, örneğin, yoğuşuğu lazer ile karıştırma veya sıkıştırılmış kapanı çevirmekle olur. Oluşturulan bu girdap kuantum girdabıdır. GPE nin lineer olmayan 







![image]()
is (girdaptan uzak yoğunluk)
![image]()
![image]()
is (İyileştirilmiş yoğuşuk uzunluğu)
Olması durumda bilgisayar yardımıyla hesaplanır. Bu doğru bir davranışı gösterir ve iyi bir yaklaşımdır. Tek taraflı yüklenen girdap (


(İyi tanımlamış bu enerjiyi elde etmek için 

Bu denklemde 
Çekici Etkileşimler
1995-2000 yılları arasında Rice Üniversitesi'nde Randall Hulet liderliğindeki deneyler, çekici etkileşimler ile lityum yoğuşukların sadece belirli bir kritik atom numarasına kadar sabit var olabileceğini gösterdi. Bu kritik katsayının ötesinde, çekimin maksimum olduğu sıfır noktasındaki harmonik hapsolmuş potansiyel enerji, süpernova patlamasını anımsatan yoğuşmuş enerjinin patlamasıyla çökmelere neden olur. Lityum atomlarının su ile soğutulmuş gazlarından, birinci yoğunlaşma büyümesi gözlemlenmiştir ve kritik atom numarasının aşılmasıyla da ani bir çöküş görülmüştür. Cornell, Wieman ve çalışma arkadaşlarının oluşturduğu JILA takımı 2000 yılında çekim yoğunlaşmaları ile ilgili daha ileri bilgiye ulaşmışlardır. Orijinal olarak anisotop (atomları birbirini iten) rubidyum 87 atomunu daha sabit yoğunlaşma oluşturmak için kullanmışlardır. Cornell ve arkadaşları yaptıkları çalışmaları daha da ilerleterek doğal çekim atomlarından diğer bir rubidyum izotopu olan ribidium-85 ile çalışmalar yapmıştır (negatif atom ve atom dağılım uzunlukları). Karakteristikleri azaltan, Rb-85 atomlarını itici ve sabit yoğunlaşmalı bir hale getiren moleküllerin rubidyum atomları ile bağladığı zamanlardaki kesintili enerjilerinin, döngüsel çevrimli çarpışmalara neden olan manyetik alan yayılımı içeren Prosese Feshbach Rezonansı denir. Çekimden itime doğru olan tersine çevrimden dalga gibi hareket eden yoğunlaşma atomları arasındaki kuantum girişimini engellemektedir.
JILA takımı manyetik alan kuvvetini arttırdığında yoğunlaşma tekrar ilgi çekmeye, genişlemeye ve büzülmeye başlar ve daha sonra 10,000 kadar atomlarının yaklaşık üçte ikisini kovarak patlar. Yoğunlaşmasının içindeki atomların yaklaşık yarısı yapılan deneylerden dolayı kaybolmuş olarak görülürken soğuk kalıntısı veya genişleyen gaz bulutu görülmez. Carl Wieman mevcut atom teorisi altında Bose-Einstein yoğunlaşması açıklayamadı çünkü mutlak sıfıra yakın bir atomun enerjisi durumu iç patlama için yeterli değildir. Bu yüzden sonraki alan teorilerinde bunu açıklamayı hedeflemiştir. Kaybolan atomlar neredeyse hala başka şekillerde varlığını sürdürüyor ama ancak deneylerle gözlemlenebiliyor. Büyük olasılıkla onlar iki bağlanmış rubidyum atomlardan oluşan molekülleri oluşturdu ve bu geçişi yaparak kazanılan enerji onların tespit edilmeden kaçmaları için yeterli bir hız kazandırdı.
Güncel araştırmalar
Maddenin daha sık karşılaşılan durumlara kıyasla, Bose-Einstein yoğunlaşmaları son derece kırılgandır. Dış dünya ile en ufak bir etkileşim onların ilginç özelliklerini ortadan kaldırılmasına ve normal oluşturan gazların yoğunlaşma eşiği geçmesine neden olur ve bu onları ısıtmak için yeterli olur.
Yine de, temel fizik soruları geniş bir yelpazede keşfetmenin yararları kanıtlanmış ve JILA ve MİT gruplar tarafından yapılan ilk keşifler sayesinde deneysel ve teorik faaliyet patlamalarını gördük. Örnekler ikiliği-parçacığa dalga nedeniyle yoğuşukların arasındaki girişimi gösteren deneylerini içerir, süper akışkanlık ve belirli dereceye kadar enerji içeren girdapların, tek boyutla sınırlı Bose yoğuşuklarında gelen aydınlık dalga solitonların oluşturulmasına ve ışık bakliyat yavaşlamasının elektromanyetik kaynaklı şeffaflık kullanılarak düşük hızları ölçmesine olanak sağlar. Uzmanlar "optik menfezler" ile örtüşen lazerlerden gelen girişim deseniyle yoğuşuk için bir periyodik potansiyel sağlamaktadır. Bunlar süper iletkende ve bir Mott yalıtıcı arasındaki geçişi araştırmak ve Örnek Tonks-Girardeau gaz için, daha az üç boyutta Bose-Einstein yoğunlaşma incelenmesinde yararlı olarak kullanılmıştır. Bose Einstein yoğunlaşması üretilen geniş aralıklı izotoplardan oluşur. İlk moleküler Bose-Einstein yoğunlaşması MIT'de Innsbruck Üniversitesinde ve Boulder Colorado Üniversitesi'nde Deborah S. Jin ve Wolfgang Ketterle Rudolf Grimm grupları tarafından 2003 yılının Kasım ayında kuruldu. Jin-Cooper çiftinden oluşan ilk fermiyonik BEC oluşturmak için hızla gitti. 1999 yılında, Danimarkalı fizikçi Lene Hau yaklaşık 17 saniyede metre başına bir ışık demetini yavaşlatmayı başardı ve Harvard Üniversitesi'nden bir ekip açtı. Bunu süper akışkan kullanarak elde etmeyi başardı. Hau ve o Harvard Üniversitesi’nde bulunan ortaklarıyla başarılı bir "ışık darbe" yoğuşukları atom grubunu geri tepme yaptırabilmişlerdir.
İzotoplar
Etkisi ağırlıklı olarak nükleer özellikli tuzaklar için alkali atomları üzerinde gözlenme yapılmıştır. 2012 yılı itibarıyla, ultra-düşük sıcaklık olan 10−7 K ya da daha altı kullanılarak, Bose-Einstein yoğuşukları, yoğun ağırlıklı alkali, toprak alkali ve lantan atomları için elde edilir (7Li, 23Na, 39K, 41K, 85Rb, 87Rb, 133Cs, 52Cr, 40Ca, 84Sr, 86Sr, 88Sr, 174Yb, 164Dy ve 168Er). Yoğunlaşma araştırmaları daha da özel yöntemler yardımı ve hidrojen ile en sonunda başarı elde etmiştir. ===Bose-Einstein yoğunlaşması===bozonlardan oluşan maddelerin mutlak sıfır sıcaklığına çok yakın değerlere kadar soğutulmasıyla ortaya çıkan maddenin bir halidir. Bu süpersoğutulmuş maddede atomların büyük çoğunluğu en düşük kuantum durumlarına çöker ve böylece makroskopik skalada kuantum etkileri göstermeye başlar. Maddenin bu hali, Satyendra Nath Bose'un yaptığı çalışmalar üzerine 1925'te Albert Einstein tarafından kuantum mekaniğinin bir sonucu olarak tahmin edilmişti. Yetmiş yıl sonra 1995'te ilk yoğunlaşma Eric Cornell ve Carl Wieman tarafından NIST-JILA laboratuvarında rubidyum gazını 170 nanoKelvin'e (nK) soğutarak elde edildi. Cornell, Wieman ve MIT'den Wolfgang Ketterle bu deneyle 2001 Nobel Fizik Ödülü paylaştılar.
Kaynakça
- ^ Pethick, C.J. (2001). Bose-Einstein Condensate in Dilute Gases (1 bas.). Cambridge University Press. s. 416. ISBN .
- ^ Arora, C. P. (2001). Thermodynamics. Tata McGraw-Hill. s. 43. ISBN . 27 Mayıs 2013 tarihinde kaynağından . Erişim tarihi: 5 Eylül 2014., Table 2.4 page 43 27 Mayıs 2013 tarihinde Wayback Machine sitesinde .
- ^ . Lorentz.leidenuniv.nl. 27 Ekim 1920. 19 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Mart 2011.
- ^ Clark, Ronald W. (1971). Einstein: The Life and Times. Avon Books. ss. 408-409. ISBN .
- ^ London, F. (1938). "The λ-Phenomenon of Liquid Helium and the Bose–Einstein Degeneracy". Nature. 141 (3571). ss. 643-644. Bibcode:1938Natur.141..643L. doi:10.1038/141643a0.
- ^ London, F. Superfluids Vol.I and II, (reprinted New York: Dover 1964)
- ^ . NIST. 28 Nisan 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Eylül 2014.
- ^ Levi, Barbara Goss (2001). . Search & Discovery. Physics Today online. 24 Ekim 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Ocak 2008.
- ^ Klaers, Jan; Schmitt, Julian; Vewinger, Frank; Weitz, Martin (2010). "Bose–Einstein condensation of photons in an optical microcavity". Nature. 468 (7323). ss. 545-548. arXiv:1007.4088 $2. Bibcode:2010Natur.468..545K. doi:10.1038/nature09567. (PMID) 21107426.
- ^ (OEIS'de A078434 dizisi)
- ^ "Belgelerle Türk tarihi dergisi, 80-83. sayılar". 2 Şubat 2014 tarihinde kaynağından . Erişim tarihi: 29 Ekim 2012.
^ Arora, C. P. (2001). Thermodynamics. Tata McGraw-Hill. p. 43. ., Table 2.4 page 43 Jump up ^ "Leiden University Einstein archive". Lorentz.leidenuniv.nl. 27 Ekim 1920. Retrieved 23 Mart 2011. Jump up ^ Clark, Ronald W. (1971). Einstein: The Life and Times. Avon Books. pp. 408–409. . Jump up ^ London, F. (1938). "The λ-Phenomenon of Liquid Helium and the Bose–Einstein Degeneracy". Nature 141 (3571): 643–644. Bibcode:1938Natur.141..643L. doi:10.1038/141643a0. Jump up ^ London, F. Superfluids Vol.I and II, (reprinted New York: Dover 1964) Jump up ^ "New State of Matter Seen Near Absolute Zero". NIST. Jump up ^ Levi, Barbara Goss (2001). "Cornell, Ketterle, and Wieman Share Nobel Prize for Bose–Einstein Condensates". Search & Discovery. Physics Today online. Archived from the original on 24 Ekim 2007. Retrieved 26 Ocak 2008. Jump up ^ Klaers, Jan; Schmitt, Julian; Vewinger, Frank; Weitz, Martin (2010). "Bose–Einstein condensation of photons in an optical microcavity". Nature 468 (7323): 545–548. arXiv:1007.4088. Bibcode:2010Natur.468..545K. doi:10.1038/nature09567. PMID 21107426. Jump up ^ Sob'yanin, D. N. (2013). "Theory of Bose-Einstein condensation of light in a microcavity". Bull. Lebedev Phys. Inst. 40 (4): 91–96. arXiv:1308.4089. Bibcode:2013BLPI...40...91S. doi:10.3103/S1068335613040039. Jump up ^ Sob'yanin, Denis Nikolaevich (2013). "Bose-Einstein condensation of light: General theory". Phys. Rev. E 88 (2): 022132. arXiv:1308.4090. Bibcode:2013PhRvE..88b2132S. doi:10.1103/PhysRevE.88.022132. PMID 24032800. Jump up ^ (sequence A078434 in OEIS) Jump up ^ Beliaev, S. T. Zh. Eksp. Teor. Fiz. 34, 418–432 (1958); ibid. 433–446 [Soviet Phys. JETP 3, 299 (1957)]. Jump up ^ Schick, M. (1971). "Two-Dimensional System of Hard-Core Bosons". Physical Review A 3 (3): 1067. Bibcode:1971PhRvA...3.1067S. doi:10.1103/PhysRevA.3.1067. edit Jump up ^ Kolomeisky, E.; Straley, J. (1992). "Renormalization-group analysis of the ground-state properties of dilute Bose systems in d spatial dimensions". Physical Review B 46 (18): 11749. Bibcode:1992PhRvB..4611749K. doi:10.1103/PhysRevB.46.11749. edit Jump up ^ Kolomeisky, E. B.; Newman, T. J.; Straley, J. P.; Qi, X. (2000). "Low-Dimensional Bose Liquids: Beyond the Gross-Pitaevskii Approximation". Physical Review Letters 85 (6): 1146–1149. arXiv:cond-mat/0002282. Bibcode:2000PhRvL..85.1146K. doi:10.1103/PhysRevLett.85.1146. PMID 10991498. edit Jump up ^ Chui, S.; Ryzhov, V. (2004). "Collapse transition in mixtures of bosons and fermions". Physical Review A 69 (4). Bibcode:2004PhRvA..69d3607C. doi:10.1103/PhysRevA.69.043607. edit Jump up ^ Salasnich, L.; Parola, A.; Reatto, L. (2002). "Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates". Phys. Rev. A 65 (4): 043614. arXiv:cond-mat/0201395. Bibcode:2002PhRvA..65d3614S. doi:10.1103/PhysRevA.65.043614. Jump up ^ Avdeenkov, A. V.; Zloshchastiev, K. G. (2011). "Quantum Bose liquids with logarithmic nonlinearity: Self-sustainability and emergence of spatial extent". J. Phys. B: At. Mol. Opt. Phys. 44 (19): 195303. arXiv:1108.0847. Bibcode:2011JPhB...44s5303A. doi:10.1088/0953-4075/44/19/195303. ^ Jump up to: a b "Eric A. Cornell and Carl E. Wieman — Nobel Lecture" (PDF). nobelprize.org. Jump up ^ Bradley, C. C.; Sackett, C. A.; Tollett, J. J.; Hulet, R. G. (1995). "Evidence of Bose-Einstein Condensation in an Atomic Gas with Attractive Interactions". Physical review letters 75 (9): 1687–1690. doi:10.1103/PhysRevLett.75.1687. PMID 10060366. edit Jump up ^ Nikuni, T.; Oshikawa, M.; Oosawa, A.; Tanaka, H. (1999). "Bose–Einstein Condensation of Dilute Magnons in TlCuCl3". Physical Review Letters 84 (25): 5868–71. arXiv:cond-mat/9908118. Bibcode:2000PhRvL..84.5868N. doi:10.1103/PhysRevLett.84.5868. PMID 10991075. Jump up ^ Demokritov, S.O.; Demidov, VE; Dzyapko, O; Melkov, GA; Serga, AA; Hillebrands, B; Slavin, AN (2006). "Bose–Einstein condensation of quasi-equilibrium magnons at room temperature under pumping". Nature 443 (7110): 430–433. Bibcode:2006Natur.443..430D. doi:10.1038/nature05117. PMID 17006509. Jump up ^ Magnon Bose Einstein Condensation made simple. Website of the "Westfählische Wilhelms Universität Münster" Prof.Demokritov. Retrieved 25 Haziran 2012. Jump up ^ Baierlein, Ralph (1999). Thermal Physics. Cambridge University Press. . Jump up ^ Becker, Christoph; Stellmer, Simon; Soltan-Panahi, Parvis; Dörscher, Sören; Baumert, Mathis; Richter, Eva-Maria; Kronjäger, Jochen; Bongs, Kai; Sengstock, Klaus (2008). "Oscillations and interactions of dark and dark–bright solitons in Bose–Einstein condensates". Nature Physics 4 (6): 496–501. arXiv:0804.0544. Bibcode:2008NatPh...4..496B. doi:10.1038/nphys962. Jump up ^ van Putten, M.H.P.M. (2010). "Pair condensates produced in bosenovae". Physics Letters A 374 (33): 3346. Bibcode:2010PhLA..374.3346V. doi:10.1016/j.physleta.2010.06.020. Jump up ^ Gorlitz, Axel. "Interference of Condensates (BEC@MIT)". Cua.mit.edu. Retrieved 13 Ekim 2009. Jump up ^ Dutton, Zachary; Ginsberg, Naomi S.; Slowe, Christopher and Hau, Lene Vestergaard (2004). "The art of taming light: ultra-slow and stopped light". Europhysics News 35 (2): 33. Bibcode:2004ENews..35...33D. doi:10.1051/epn:2004201. Jump up ^ "From Superfluid to Insulator: Bose–Einstein Condensate Undergoes a Quantum Phase Transition". Qpt.physics.harvard.edu. Retrieved 13 Ekim 2009. Jump up ^ "Ten of the best for BEC". Physicsweb.org. 1 Haziran 2005. Jump up ^ "Fermionic condensate makes its debut". Physicsweb.org. 28 Ocak 2004. Jump up ^ Cromie, William J. (18 Şubat 1999). "Physicists Slow Speed of Light". The Harvard University Gazette. Retrieved 26 Ocak 2008. Jump up ^ Ginsberg, N. S.; Garner, S. R.; Hau, L. V. (2007). "Coherent control of optical information with matter wave dynamics". Nature 445 (7128): 623–626. doi:10.1038/nature05493. PMID 17287804. edit Jump up ^ Weiss, P. (12 Şubat 2000). "Atomtronics may be the new electronics". Science News Online 157 (7): 104. doi:10.2307/4012185. Retrieved 12 Şubat 2011. Jump up ^ Tannenbaum, Emmanuel David (1970). "Gravimetric Radar: Gravity-based detection of a point-mass moving in a static background". arXiv:1208.2377 [physics.ins-det
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Subat 2014 Bose Einstein yogunlasmasi BEY parcaciklari bozonlardan olusan maddelerin en alt enerji seviyesinde yogunlastigi kuantum etkilerinin gozlenebildigi maddenin bir halidir Bozonik atomlar icin seyreltilmis gaz halinde araciligiyla mutlak sifir sicakligina dogru inilerek 0 K veya 273 15 C ye cok yakin bu hale gecis yani yogunlasma saglanabilir Atomlarin klasik gazlardan farkli olarak Maxwell Boltzmann istatistigi yerine makroskobik olarak buyuk olcekte uymasi BEY nin belirleyici ozelligidir Bir gaz icin hiz dagilimi verileri 3 kez rubidyum maddenin yeni bir asamaya Bose Einstein yogunlasmasi ve kesif teyit atomlari Sol sadece bir Bose Einstein yogunlasmasi gorunumunu once Merkezi Sadece yogusugu gorunumunu sonra Sag sonra daha fazla buharlasmasi neredeyse saf yogusuk bir ornek Daha sonra yapilan deneylerin karmasik etkilesimler ortaya cikarmasina ragmen maddenin bu hali ilk olarak Satyendra Nath Bose ve Albert Einstein tarafindan 1924 1925 yillarinda genel olarak tahmin edildi Bose ilk olarak Einstein a isik kuanta sinin artik foton olarak adlandiriliyor kuantum istatistigiyle ilgili bir makale yollamistir Einstein bundan etkilenir ve makaleyi Ingilizce den Almanca ya cevirerek Zeitschrift fur Physik Bose icin sunar ve makale yayimlanir Einstein in baski metni bir ara kayboldugunun dusunulmesine ragmen Leiden Universitesinde 2005 yilinda bulunur Einstein daha sonra iki farkli makalede Bose un fikirlerini madde parcaciklari konusuna genisletir Bose ve Einstein in calismalari sonucunda birbiriyle es parcaciklarin tam firillarinin istatistiksel dagilimini tanimlayan simdilerde bozon olarak adlandirilan Bose Einstein istatistigi ile yonetilen Bose gazi kavrami ortaya cikmistir Einstein bozonik atomlarinin cok dusuk derecelere kadar sogumasinin yeni bir madde formu olusturarak ulasilabilir en dusuk kuantum durgusuna donustugunu gostermistir 1938 yilinda Fritz London BEC yi 4He un ustun akiskanlik ve ustun iletkenlik mekanizmasiyla tasarladi 1995 yilinda ilk gaz yogunlasmasi Eric Cornell ve Carl Wieman tarafindan University of Colorado ar Boulder NIST JILA laboratuvarinda rubidyum atomu gazlarinin 170 nanokelvin nK e 1 7 10 7 K sogutulmasiyla uretilmistir Bu basarilariyla Cornell Wieman ve Wolfgang Ketterle MIT de 2001 Nobel Fizik Odulunu almistir Kasim 2010 da ilk BEC fotonu gozlemlenmistir 2012 de ise BEC foton teorisi gelistirilmistir 9 10 9 10 Bu BEC ye gecis belirgin icsel serbestlik derecesi ile etkilesmeyen parcaciklar iceren uc boyutlu uniform gazlarin kritik sicakligin altinda olusur Tc nz 3 2 2 32pℏ2mkB 3 3125 ℏ2n2 3mkB displaystyle T c left frac n zeta 3 2 right 2 3 frac 2 pi hbar 2 mk B approx 3 3125 frac hbar 2 n 2 3 mk B Tc displaystyle T c kritik sicaklik n displaystyle n m displaystyle m bozon basina dusen kutle ℏ displaystyle hbar indirgenmis Planck sabiti kB displaystyle k B Boltzmann sabitiz displaystyle zeta Riemann zeta fonksiyonu z 3 2 2 6124 displaystyle zeta 3 2 approx 2 6124 Einstein in argumani N tane her biri iki kuantum durgusundan birinde olan 0 displaystyle scriptstyle 0 rangle ve 1 displaystyle scriptstyle 1 rangle etkilesmeyen parcaciklardan olusan bir koleksiyon dusunun Eger bu iki hal enerjice esitse her farkli yapilandirma esit sanslidir Eger her parcaciklarin hangi parcacik oldugunu bilirsek ve eger her parcacik bagimsiz olarak 0 displaystyle scriptstyle 0 rangle ya da 1 displaystyle scriptstyle 1 rangle icinde olursa 2N displaystyle 2 N tane farkli yapilandirma olur Neredeyse her yapilandirmalarinda parcaciklarin yaklasik yarisi 0 displaystyle scriptstyle 0 rangle diger yarisi 1 displaystyle scriptstyle 1 rangle kapsamindadir Dengesi ise istatistiksel bir etkidir parcaciklar esit dagildiginda yapilandirma en buyuktur Eger parcaciklar birbirinden ayirt edilemezse sadece N 1 yapilandirma olur K tane parcacigin 1 displaystyle scriptstyle 1 rangle halinde tane parcacik 0 displaystyle scriptstyle 0 rangle halinde olur Partikullerin 1 displaystyle scriptstyle 1 rangle ya da 0 displaystyle scriptstyle 0 rangle halinde olmasi ayirt edilemese de her Kdegeri tum sistemin kuantum durgusunu belirler Tum durumlarin esit sansli oldugu durumlarda istatistiksel bir dagilma olmaz Bu durum sadece tum parcaciklarin yari yariya dagilirken tum parcaciklarin 0 displaystyle scriptstyle 0 rangle halinde olmasi kadar muhtemeldir Ayirt edilebilir durumda daha buyuk N sayilari icin 0 displaystyle scriptstyle 0 rangle halindeki kisim hesaplanabilir Bu durum tamamen bir bozuk paranin tura gelme olasiligi olan p exp E T kadardir Yazi gelme olasiligi ise p nin ve enerjinin olan denklemine esittir Ayirt edilemez durumlarda her K kendi ayri Boltzman olasiligina sahip tek haldedir Bu yuzden dagilim olasiligi usludur P K Ce KE T CpK displaystyle P K Ce KE T Cp K Daha buyuk N degerleri icin C normallestirme sabiti Beklenilen toplam parcacik sayilari en dusuk enerji durumunda degildir eger limit N displaystyle scriptstyle N rightarrow infty iken n gt 0Cnpn p 1 p displaystyle scriptstyle sum n gt 0 Cnp n p 1 p e esittir Bu durum Nsayisi buyukken degil sadece sabit degere ulastigi durumda gelisir Bu parcaciklarin toplam sayisinin ihmal edilebilir kismindadir Bu yuzden termal dengede olan yeterli sayidaki Boz parcaciklar cogunlukla temel durumdadir Enerji degisimi cok kucuk olsa bile sadece cok az parcacik uyarilmis durumdadir k displaystyle scriptstyle k rangle Olarak isimlendirilen degisik bir momentum durumunda olan bir gaz parcacigi dusunelim Eger yuksek ve dusuk yogunluklar icin parcaciklarin toplam sayisi termal olarak ulasilabilir parcaciklarin sayisindan az ise her bir parcacik ayri bir halde olacaktir Bu limitler icerisinde gaz klasiktir Yogunluk arttiginda ya da sicaklik dustugunde parcacik basina dusen ulasilabilir durum kuculur Bu noktada izin verilen istatistiksel agirliktan daha cok parcacik tek duruma gecmek icin zorlanacaktir Bu noktadan sonra herhangi ekstra parcacik temel seviyeye eklenecektir Herhangi bir yogunlukta butunlemede tum momentum durumlarinin uzerinde degisim sicakligini hesaplamak icin maksimum sayidaki uyarilmis parcaciklar N V d3k 2p 3p k 1 p k V d3k 2p 31ek22mT 1 displaystyle N V int d 3 k over 2 pi 3 p k over 1 p k V int d 3 k over 2 pi 3 1 over e k 2 over 2mT 1 p k e k22mT displaystyle p k e k 2 over 2mT Tumlev kB ve ℏ faktorleri ile degerlendirilir ve boyutlu analizlerle yenilestirilirse ilerleyen kisimlarda kritik sicaklik formulunu verecektir Bu yuzden bu tumlev kritik sicaklik ve ihmal edilen kimyasal potansiyele karsilik gelen parcacik sayilarini tanimlar Bose Einstein istatistiksel dagiliminda m hala BEC nin sifir olmayan fakat temel durum enerjisinden dusuktur Ozellikle temel durumdan bahsetmek disinda m cogunluk enerji ve momentum durumuna yaklastirilir as m 0 daki gibi Gross Pitaevskii Denklemi Ana makale Gross Pitaevskii denklemi BEC nin bu durumu yogusuk ps r displaystyle psi vec r un dalga denklemi ile tanimlanir Bu yapidaki bir sistemde ps r 2 displaystyle psi vec r 2 parcacik yogunlugu olarak yorumlanir Bu yuzden toplam atomlarin sayisi N dr ps r 2 displaystyle N int d vec r psi vec r 2 dir Saglanan tum gerekli atomlar yogusuk iken temel seviyeye yogusan bozonlar ana alan teorisini tehdit ederler ps r displaystyle psi vec r Durumu ile alakali enerji E ise E dr ℏ22m ps r 2 V r ps r 2 12U0 ps r 4 displaystyle E int d vec r left frac hbar 2 2m nabla psi vec r 2 V vec r psi vec r 2 frac 1 2 U 0 psi vec r 4 right dir ps r displaystyle psi vec r iken sonsuz derecede kucuk degisimleri baz alan enerjiyi kucultmek ve atom sayilarini sabit tutmak Gross Pitaevskii denklemini GPE ortaya cikarir lineer olmayan Schrodinger denklemi olarak da bilinir iℏ ps r t ℏ2 22m V r U0 ps r 2 ps r displaystyle i hbar frac partial psi vec r partial t left frac hbar 2 nabla 2 2m V vec r U 0 psi vec r 2 right psi vec r m displaystyle m bozonlarin kutlesi V r displaystyle V vec r dis potensiyeli U0 displaystyle U 0 parcacik arasi etkilesimleri GPE BEC lerin davranislari ile ilgili iyi tanimlar ortaya koyar ve bu yuzden teorik analizlerde kullanilir Gross Pitaevskii haricindeki modeller BEC nin Gross Pitaeyskii modeli BEC nin belirli siniflari icin gecerli olan fiziksel bir yaklasimdir Yapi itibariyla GPE su basitlestirmeyi kullanmaktadir GPE yogun parcaciklar arasindaki etkilesimlerin iki body tipinden kaynaklandigini farz eder ve serbest enerjinin buyuk katkisini yok sayar Bu varsayimlar genellikle seyreltilmis 3 boyutlu yogusuklar icin uygundur Eger bu varsayimlardan biri olmazsa yogusuk dalga fonksiyonu wavefunction yuksek dereceli terimler icerir Hatta bazi fiziksel sistemler icin terim miktari sonsuza kadar gider ve denklem polinom olmaz Bu durumun meydana geldigi ornekler Bose Fermi birlesik yogusuklar etkili dusuk boyutlu yogusuklar yogun yogusuklar ve super akiskan super sivi mutlak sifirin bir derece ustundeki sivi hali kabuklar ve damlaciklar Kesif 1938 yilinda Pyotr Kapitsa John Allen ve Don Misener super akiskan olarak bilinen ve 2 17 Kelvin den dusuk sicakliktaki helium 4 u kesfettiler Super akiskan helium sifir adalilik ve sayisal girdap quantized vortices gibi olagan disi bircok ozellik icerir Oncelikle super akiskanligin sivinin kismi Bose Einstein yogunlugundan dolayi olduguna inanildi Aslinda super akiskan helyumun cogu ozelligi Cornell Wieman ve Ketterle tarafindan olusturulan gazli Bose Einstein yogusuklarinda gorulmektedir Super akiskan helium 4 gazdan ziyade sividir Yani atomlar arasindaki etkilesimler goreceli olarak gucludur Bose Einstein inin yogunlasma teorisi Super akiskan helium 4 u tanimlamak icin ciddi sekilde degistirilmelidir Ayrica bozon yerine fermiyum iceren helium 3 dusuk sicaklikta super akiskan hale gecer Bu durum 2 atomlu bozonik Cooper cifti bicimlenme ile aciklanabilir Ilk saf Bose Einstein yogusugu 5 Haziran 1995 yilinda Eric Cornell Carl Wieman ve JILA daki meslektaslari tarafindan olusturuldu Bu calismayi lazer sogutucu ve manyetik buharlasmali sogutucu kullanarak 170 NK dan dusuk yaklasik 2 bin rubidiim 87 atomu iceren seyreltilmis buhari sogutarak yapmislardir 4 ay sonra MIT ten Wolfgang Ketterle sodium 23 ten yapilmis bir yoguskani olusturdu Ketterle nin yoguskani yaklasik 100 kat daha fazla atom icerir Bu durum ona 2 farkli yogunlasma arasinda kuantum mekanik etkilesiminin gozlemlenmesi gibi onemli sonuclar saglar Cornell Wieman ve Ketterle basarilari icin 2001 yilinda Nobel Fizik Odulu nu kazanmislardir JILA calismasindan bir ay sonra Rice Universitesinde Randall Hulet onderligindeki bir grup Lithium atomlarinin yogusugu olusturduklarini duyurmuslardir Lithium yogusugu duraksiz olmasina ve atomlarin carpismasina neden olan ilginc etkilesimler gostermektedir Hulet ve meslektaslari bir sonraki denemede yogusugu yaklasik 1000 atoma kadar kuantum basinci ile dengelenebilecegini gostermistir Bose Einstein yogunlasmasi ayrica katilarda sanki parcaciklara uygulanabilir Antiferromagnetteki bir magnon donme 1 tasir ve Bose Einstein statigine uyar Magnonlarin yogunluklari dis manyetik alani tarafindan kontrol edilir Bu teknik Bose sivisiyla guclu bir etkilesime giren seyreltilmis Bose gazindan genis aralikta bozon yogunluklarina ulasabilmeyi saglar Yogunlasma noktasinda gozlemlenen manyetik siralanma super akiskanlik analogudur 1999 da magnonlarin Bose yogunlasmasi antiferromagnet Tl Cu Cl3 icerisinde gosterilmistir Yogunlasma 14 K kadar yuksek sicakliklarda gozlenmistir Yuksek sicakliga gecisin nedeni magnonlarin daha yuksek yogunlukta ve daha kucuk kutlede olmasidir 2006 yilinda ferromagnetlerdeki magnonlarin yogunlasmasi oda sicakliginda gosterilmistir Hiz Dagilimi GrafigiBu makaleye eslik eden figurde hiz dagilim bilgisi gaz halindeki rubidyum atomlarinin Bose Einstein yogusugu olusturmasini isaret eder Sahte renkler her hizdaki atomlarin sayilarini belirtir kirmizi en az sayida beyaz en cok sayida Beyaz ve acik mavi renkleriyle gorulen alanlar en dusuk hizlari temsil eder Zirve Heisenberg belirsizlik prensibinden dolayi sonsuz degildir Atomlar boslukta belirli bir alanda sikismadigi surece hiz dagilimlari belirli bir minimum genisliktedir Bu genislik manyetik sikisma potansiyelin egriligi tarafindan belirlenir Daha sikica kapatilmis yonler daha buyuk genislikte hiz dagilimlarina sahiptir Bu anizotropinin sagdaki zirvesi saf kuantum mekanigi etkisidir ve soldaki normal dagilimda bulunmaz Bu grafik 1999 da Ralph Baierlein tarafindan yazilan Thermal Physics 24 kitabinin kapaginda kullanilmistir Girdaplar Bircok sistemde oldugu gibi BEC lerde de bazi girdaplar bulunmaktadir Bu girdaplar ornegin yogusugu lazer ile karistirma veya sikistirilmis kapani cevirmekle olur Olusturulan bu girdap kuantum girdabidir GPE nin lineer olmayan ps r 2 displaystyle psi vec r 2 terimleriyle bu gorungulerine musaade edilir Bu girdaplar mutlaka dalga denklemlerinin nicellenmis quantized acisal momentumlari icermelidir Bu dalga denklemleri r z displaystyle rho z ve 8 displaystyle theta silindirik koordinat sistemleri ve ℓ displaystyle ell acisal numara iken ps r ϕ r z eiℓ8 displaystyle psi vec r phi rho z e i ell theta formunda olmalidir Bu belirli olarak genellikle kullanilan eklensel olarak simetrik mesela harmonik sikistirilma potansiyeline sahiptir Bu kavram kolaylikla genellestirilebilir ps r ϕ r z eiℓ8 displaystyle psi vec r phi rho z e i ell theta Denklemine gore ϕ r z displaystyle phi rho z yi hesaplayabilmek icin ps r displaystyle psi vec r in enerjisi minimize edilmelidir Bu islem tekduze ortamlarda analitik formun ϕ nx2 x2 displaystyle phi frac nx sqrt 2 x 2 n2 displaystyle n 2 is girdaptan uzak yogunluk x rℓ3 displaystyle x frac rho ell xi 3 displaystyle xi is Iyilestirilmis yogusuk uzunlugu Olmasi durumda bilgisayar yardimiyla hesaplanir Bu dogru bir davranisi gosterir ve iyi bir yaklasimdir Tek tarafli yuklenen girdap ℓ 1 displaystyle ell 1 temel durumdadir ve enerjisi ϵv displaystyle epsilon v tarafindan belirlenir ϵv pnℏ2mln 1 464b3 displaystyle epsilon v pi n frac hbar 2 m ln left 1 464 frac b xi right b displaystyle b Girdaptan en uzak mesafede Iyi tanimlamis bu enerjiyi elde etmek icin b displaystyle b sinirini kapsamasi gerekir Coklu yuklenen girdaplarda ℓ gt 1 displaystyle ell gt 1 enerji asagidaki denkleme yaklastirilir ϵv ℓ2pnℏ2mln b3 displaystyle epsilon v approx ell 2 pi n frac hbar 2 m ln left frac b xi right Bu denklemde ℓ displaystyle ell tekli yuklenen girdaptan buyuktur ve bu coklu yuklenen girdaplarin bozunmaya dayaniksiz oldugunu gosterir Bu calisma ayrica metastabl durumlarda daha uzun yasam suresi oldugunu da gosterdi BEC lerde girdap olusumunu tek yonlu koyu solitonlarin olusumu ile yakindan iliskilidir Bu topolojik objeler dugum yuzeylerde faz yontu turevi belirtir ve bu da seklini yayilma ve etkilesimde korumasini saglar Solusyonlar hic yuk tasimasa veya curumeye meyilli olsa bile nispeten uzun omurlu koyu solutanlar uretilmis ve yogun olarak calisilmistir Cekici Etkilesimler 1995 2000 yillari arasinda Rice Universitesi nde Randall Hulet liderligindeki deneyler cekici etkilesimler ile lityum yogusuklarin sadece belirli bir kritik atom numarasina kadar sabit var olabilecegini gosterdi Bu kritik katsayinin otesinde cekimin maksimum oldugu sifir noktasindaki harmonik hapsolmus potansiyel enerji supernova patlamasini animsatan yogusmus enerjinin patlamasiyla cokmelere neden olur Lityum atomlarinin su ile sogutulmus gazlarindan birinci yogunlasma buyumesi gozlemlenmistir ve kritik atom numarasinin asilmasiyla da ani bir cokus gorulmustur Cornell Wieman ve calisma arkadaslarinin olusturdugu JILA takimi 2000 yilinda cekim yogunlasmalari ile ilgili daha ileri bilgiye ulasmislardir Orijinal olarak anisotop atomlari birbirini iten rubidyum 87 atomunu daha sabit yogunlasma olusturmak icin kullanmislardir Cornell ve arkadaslari yaptiklari calismalari daha da ilerleterek dogal cekim atomlarindan diger bir rubidyum izotopu olan ribidium 85 ile calismalar yapmistir negatif atom ve atom dagilim uzunluklari Karakteristikleri azaltan Rb 85 atomlarini itici ve sabit yogunlasmali bir hale getiren molekullerin rubidyum atomlari ile bagladigi zamanlardaki kesintili enerjilerinin dongusel cevrimli carpismalara neden olan manyetik alan yayilimi iceren Prosese Feshbach Rezonansi denir Cekimden itime dogru olan tersine cevrimden dalga gibi hareket eden yogunlasma atomlari arasindaki kuantum girisimini engellemektedir JILA takimi manyetik alan kuvvetini arttirdiginda yogunlasma tekrar ilgi cekmeye genislemeye ve buzulmeye baslar ve daha sonra 10 000 kadar atomlarinin yaklasik ucte ikisini kovarak patlar Yogunlasmasinin icindeki atomlarin yaklasik yarisi yapilan deneylerden dolayi kaybolmus olarak gorulurken soguk kalintisi veya genisleyen gaz bulutu gorulmez Carl Wieman mevcut atom teorisi altinda Bose Einstein yogunlasmasi aciklayamadi cunku mutlak sifira yakin bir atomun enerjisi durumu ic patlama icin yeterli degildir Bu yuzden sonraki alan teorilerinde bunu aciklamayi hedeflemistir Kaybolan atomlar neredeyse hala baska sekillerde varligini surduruyor ama ancak deneylerle gozlemlenebiliyor Buyuk olasilikla onlar iki baglanmis rubidyum atomlardan olusan molekulleri olusturdu ve bu gecisi yaparak kazanilan enerji onlarin tespit edilmeden kacmalari icin yeterli bir hiz kazandirdi Guncel arastirmalar Maddenin daha sik karsilasilan durumlara kiyasla Bose Einstein yogunlasmalari son derece kirilgandir Dis dunya ile en ufak bir etkilesim onlarin ilginc ozelliklerini ortadan kaldirilmasina ve normal olusturan gazlarin yogunlasma esigi gecmesine neden olur ve bu onlari isitmak icin yeterli olur Yine de temel fizik sorulari genis bir yelpazede kesfetmenin yararlari kanitlanmis ve JILA ve MIT gruplar tarafindan yapilan ilk kesifler sayesinde deneysel ve teorik faaliyet patlamalarini gorduk Ornekler ikiligi parcaciga dalga nedeniyle yogusuklarin arasindaki girisimi gosteren deneylerini icerir super akiskanlik ve belirli dereceye kadar enerji iceren girdaplarin tek boyutla sinirli Bose yogusuklarinda gelen aydinlik dalga solitonlarin olusturulmasina ve isik bakliyat yavaslamasinin elektromanyetik kaynakli seffaflik kullanilarak dusuk hizlari olcmesine olanak saglar Uzmanlar optik menfezler ile ortusen lazerlerden gelen girisim deseniyle yogusuk icin bir periyodik potansiyel saglamaktadir Bunlar super iletkende ve bir Mott yalitici arasindaki gecisi arastirmak ve Ornek Tonks Girardeau gaz icin daha az uc boyutta Bose Einstein yogunlasma incelenmesinde yararli olarak kullanilmistir Bose Einstein yogunlasmasi uretilen genis aralikli izotoplardan olusur Ilk molekuler Bose Einstein yogunlasmasi MIT de Innsbruck Universitesinde ve Boulder Colorado Universitesi nde Deborah S Jin ve Wolfgang Ketterle Rudolf Grimm gruplari tarafindan 2003 yilinin Kasim ayinda kuruldu Jin Cooper ciftinden olusan ilk fermiyonik BEC olusturmak icin hizla gitti 1999 yilinda Danimarkali fizikci Lene Hau yaklasik 17 saniyede metre basina bir isik demetini yavaslatmayi basardi ve Harvard Universitesi nden bir ekip acti Bunu super akiskan kullanarak elde etmeyi basardi Hau ve o Harvard Universitesi nde bulunan ortaklariyla basarili bir isik darbe yogusuklari atom grubunu geri tepme yaptirabilmislerdir Izotoplar Etkisi agirlikli olarak nukleer ozellikli tuzaklar icin alkali atomlari uzerinde gozlenme yapilmistir 2012 yili itibariyla ultra dusuk sicaklik olan 10 7 K ya da daha alti kullanilarak Bose Einstein yogusuklari yogun agirlikli alkali toprak alkali ve lantan atomlari icin elde edilir 7Li 23Na 39K 41K 85Rb 87Rb 133Cs 52Cr 40Ca 84Sr 86Sr 88Sr 174Yb 164Dy ve 168Er Yogunlasma arastirmalari daha da ozel yontemler yardimi ve hidrojen ile en sonunda basari elde etmistir Bose Einstein yogunlasmasi bozonlardan olusan maddelerin mutlak sifir sicakligina cok yakin degerlere kadar sogutulmasiyla ortaya cikan maddenin bir halidir Bu supersogutulmus maddede atomlarin buyuk cogunlugu en dusuk kuantum durumlarina coker ve boylece makroskopik skalada kuantum etkileri gostermeye baslar Maddenin bu hali Satyendra Nath Bose un yaptigi calismalar uzerine 1925 te Albert Einstein tarafindan kuantum mekaniginin bir sonucu olarak tahmin edilmisti Yetmis yil sonra 1995 te ilk yogunlasma Eric Cornell ve Carl Wieman tarafindan NIST JILA laboratuvarinda rubidyum gazini 170 nanoKelvin e nK sogutarak elde edildi Cornell Wieman ve MIT den Wolfgang Ketterle bu deneyle 2001 Nobel Fizik Odulu paylastilar Kaynakca Pethick C J 2001 Bose Einstein Condensate in Dilute Gases 1 bas Cambridge University Press s 416 ISBN 9780511048845 Arora C P 2001 Thermodynamics Tata McGraw Hill s 43 ISBN 0 07 462014 2 27 Mayis 2013 tarihinde kaynagindan Erisim tarihi 5 Eylul 2014 Table 2 4 page 43 27 Mayis 2013 tarihinde Wayback Machine sitesinde Lorentz leidenuniv nl 27 Ekim 1920 19 Mayis 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Mart 2011 Clark Ronald W 1971 Einstein The Life and Times Avon Books ss 408 409 ISBN 0 380 01159 X London F 1938 The l Phenomenon of Liquid Helium and the Bose Einstein Degeneracy Nature 141 3571 ss 643 644 Bibcode 1938Natur 141 643L doi 10 1038 141643a0 London F Superfluids Vol I and II reprinted New York Dover 1964 NIST 28 Nisan 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Eylul 2014 Levi Barbara Goss 2001 Search amp Discovery Physics Today online 24 Ekim 2007 tarihinde kaynagindan arsivlendi Erisim tarihi 26 Ocak 2008 Klaers Jan Schmitt Julian Vewinger Frank Weitz Martin 2010 Bose Einstein condensation of photons in an optical microcavity Nature 468 7323 ss 545 548 arXiv 1007 4088 2 Bibcode 2010Natur 468 545K doi 10 1038 nature09567 PMID 21107426 OEIS de A078434 dizisi Belgelerle Turk tarihi dergisi 80 83 sayilar 2 Subat 2014 tarihinde kaynagindan Erisim tarihi 29 Ekim 2012 Arora C P 2001 Thermodynamics Tata McGraw Hill p 43 ISBN 0 07 462014 2 Table 2 4 page 43 Jump up Leiden University Einstein archive Lorentz leidenuniv nl 27 Ekim 1920 Retrieved 23 Mart 2011 Jump up Clark Ronald W 1971 Einstein The Life and Times Avon Books pp 408 409 ISBN 0 380 01159 X Jump up London F 1938 The l Phenomenon of Liquid Helium and the Bose Einstein Degeneracy Nature 141 3571 643 644 Bibcode 1938Natur 141 643L doi 10 1038 141643a0 Jump up London F Superfluids Vol I and II reprinted New York Dover 1964 Jump up New State of Matter Seen Near Absolute Zero NIST Jump up Levi Barbara Goss 2001 Cornell Ketterle and Wieman Share Nobel Prize for Bose Einstein Condensates Search amp Discovery Physics Today online Archived from the original on 24 Ekim 2007 Retrieved 26 Ocak 2008 Jump up Klaers Jan Schmitt Julian Vewinger Frank Weitz Martin 2010 Bose Einstein condensation of photons in an optical microcavity Nature 468 7323 545 548 arXiv 1007 4088 Bibcode 2010Natur 468 545K doi 10 1038 nature09567 PMID 21107426 Jump up Sob yanin D N 2013 Theory of Bose Einstein condensation of light in a microcavity Bull Lebedev Phys Inst 40 4 91 96 arXiv 1308 4089 Bibcode 2013BLPI 40 91S doi 10 3103 S1068335613040039 Jump up Sob yanin Denis Nikolaevich 2013 Bose Einstein condensation of light General theory Phys Rev E 88 2 022132 arXiv 1308 4090 Bibcode 2013PhRvE 88b2132S doi 10 1103 PhysRevE 88 022132 PMID 24032800 Jump up sequence A078434 in OEIS Jump up Beliaev S T Zh Eksp Teor Fiz 34 418 432 1958 ibid 433 446 Soviet Phys JETP 3 299 1957 Jump up Schick M 1971 Two Dimensional System of Hard Core Bosons Physical Review A 3 3 1067 Bibcode 1971PhRvA 3 1067S doi 10 1103 PhysRevA 3 1067 edit Jump up Kolomeisky E Straley J 1992 Renormalization group analysis of the ground state properties of dilute Bose systems in d spatial dimensions Physical Review B 46 18 11749 Bibcode 1992PhRvB 4611749K doi 10 1103 PhysRevB 46 11749 edit Jump up Kolomeisky E B Newman T J Straley J P Qi X 2000 Low Dimensional Bose Liquids Beyond the Gross Pitaevskii Approximation Physical Review Letters 85 6 1146 1149 arXiv cond mat 0002282 Bibcode 2000PhRvL 85 1146K doi 10 1103 PhysRevLett 85 1146 PMID 10991498 edit Jump up Chui S Ryzhov V 2004 Collapse transition in mixtures of bosons and fermions Physical Review A 69 4 Bibcode 2004PhRvA 69d3607C doi 10 1103 PhysRevA 69 043607 edit Jump up Salasnich L Parola A Reatto L 2002 Effective wave equations for the dynamics of cigar shaped and disk shaped Bose condensates Phys Rev A 65 4 043614 arXiv cond mat 0201395 Bibcode 2002PhRvA 65d3614S doi 10 1103 PhysRevA 65 043614 Jump up Avdeenkov A V Zloshchastiev K G 2011 Quantum Bose liquids with logarithmic nonlinearity Self sustainability and emergence of spatial extent J Phys B At Mol Opt Phys 44 19 195303 arXiv 1108 0847 Bibcode 2011JPhB 44s5303A doi 10 1088 0953 4075 44 19 195303 Jump up to a b Eric A Cornell and Carl E Wieman Nobel Lecture PDF nobelprize org Jump up Bradley C C Sackett C A Tollett J J Hulet R G 1995 Evidence of Bose Einstein Condensation in an Atomic Gas with Attractive Interactions Physical review letters 75 9 1687 1690 doi 10 1103 PhysRevLett 75 1687 PMID 10060366 edit Jump up Nikuni T Oshikawa M Oosawa A Tanaka H 1999 Bose Einstein Condensation of Dilute Magnons in TlCuCl3 Physical Review Letters 84 25 5868 71 arXiv cond mat 9908118 Bibcode 2000PhRvL 84 5868N doi 10 1103 PhysRevLett 84 5868 PMID 10991075 Jump up Demokritov S O Demidov VE Dzyapko O Melkov GA Serga AA Hillebrands B Slavin AN 2006 Bose Einstein condensation of quasi equilibrium magnons at room temperature under pumping Nature 443 7110 430 433 Bibcode 2006Natur 443 430D doi 10 1038 nature05117 PMID 17006509 Jump up Magnon Bose Einstein Condensation made simple Website of the Westfahlische Wilhelms Universitat Munster Prof Demokritov Retrieved 25 Haziran 2012 Jump up Baierlein Ralph 1999 Thermal Physics Cambridge University Press ISBN 0 521 65838 1 Jump up Becker Christoph Stellmer Simon Soltan Panahi Parvis Dorscher Soren Baumert Mathis Richter Eva Maria Kronjager Jochen Bongs Kai Sengstock Klaus 2008 Oscillations and interactions of dark and dark bright solitons in Bose Einstein condensates Nature Physics 4 6 496 501 arXiv 0804 0544 Bibcode 2008NatPh 4 496B doi 10 1038 nphys962 Jump up van Putten M H P M 2010 Pair condensates produced in bosenovae Physics Letters A 374 33 3346 Bibcode 2010PhLA 374 3346V doi 10 1016 j physleta 2010 06 020 Jump up Gorlitz Axel Interference of Condensates BEC MIT Cua mit edu Retrieved 13 Ekim 2009 Jump up Dutton Zachary Ginsberg Naomi S Slowe Christopher and Hau Lene Vestergaard 2004 The art of taming light ultra slow and stopped light Europhysics News 35 2 33 Bibcode 2004ENews 35 33D doi 10 1051 epn 2004201 Jump up From Superfluid to Insulator Bose Einstein Condensate Undergoes a Quantum Phase Transition Qpt physics harvard edu Retrieved 13 Ekim 2009 Jump up Ten of the best for BEC Physicsweb org 1 Haziran 2005 Jump up Fermionic condensate makes its debut Physicsweb org 28 Ocak 2004 Jump up Cromie William J 18 Subat 1999 Physicists Slow Speed of Light The Harvard University Gazette Retrieved 26 Ocak 2008 Jump up Ginsberg N S Garner S R Hau L V 2007 Coherent control of optical information with matter wave dynamics Nature 445 7128 623 626 doi 10 1038 nature05493 PMID 17287804 edit Jump up Weiss P 12 Subat 2000 Atomtronics may be the new electronics Science News Online 157 7 104 doi 10 2307 4012185 Retrieved 12 Subat 2011 Jump up Tannenbaum Emmanuel David 1970 Gravimetric Radar Gravity based detection of a point mass moving in a static background arXiv 1208 2377 physics ins det
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State




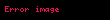













![{\displaystyle E=\int d{\vec {r}}\left[{\frac {\hbar ^{2}}{2m}}|\nabla \psi ({\vec {r}})|^{2}+V({\vec {r}})|\psi ({\vec {r}})|^{2}+{\frac {1}{2}}U_{0}|\psi ({\vec {r}})|^{4}\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aU1XUmhOVEJoWVdaaFpqRXdaRGRpWXpRd1pEWm1Oak15TXpnek4ySmlOemczWlRRME1XUmguc3Zn.svg)








