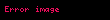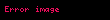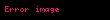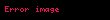Olasılık kuramı ve istatistik bilim dallarında Çebişev'in eşitsizliği veya Bienaymé-Çebişev'in eşitsizliği özellikle olasılık ve daha nadiren gerçek veri setleri için bir teori sonucu olarak kullanılır.

Bu eşitsizliğin önemi herhangi bir örneklem verisi veya olasılık dağılımı için veri değerlerinin "hemen tümü"nün ortalama değerine "yakın" olduğunu sağlamasındandır. Daha matematiksel bir ifade ile bir veri veya olasılık dağılımı değerlerinin (1/k2) oranından daha büyük olmayan oranının ortalamadan artı ve eksi k standart sapma açıklığı dışında bulunamayacağını bildirir. Bu eşitsizliğin geniş bir kapsamı vardır; zira sadece ortalama ve standart sapma verilirse, diğer her türlü niteliği hiç bilinmeyen veri veya olasılık dağılımlarına uygulanabilir.
Eşitsizliğin ifade edilme şekilleri
Olasılık kavramları ile ifade
Beklenen değeri μ ve sonsuz olmayan varyansı σ2 olan bir rassal değişken olan X değişkenini ele alalım. O zaman, herhangi bir gerçel sayı olan k > 0, için
olur. Burada sadece k > 1 koşuluna uyan değerler kullanışlı bilgi sağlamaktadır. Bunun diğer eşit bir şekilde ifade edilmesi şöyle olur:
Örnek olarak k = √2 değerini alırsak; değerlerin asgari yarısının şu açıklık içinde bulunduğunu bu eşitsizliğe göre kabul ederiz:
(μ − √2 σ, μ + √2 σ).
Sadece ortalaması ve standart sapması bilinen ve her türlü diğer nitelikleri hiç bilinmeyen dağılım veya verilere uygulandığı için ortaya çıkan sonuç, dağılımı daha tam olarak bilinen veri dağılımlardan ortaya çıkarabileceğimiz sonuçlardan daha fena sınırlar şeklinde olmaktadır.
Örneğin, elle yapılan dolum ortalama olarak 1.000 gram ağırlık vermektedir ve dolum ağırlığının standart dağılımı da 200 gramdır. O zaman bu tip bir dolum ağırlığını 600 ile 1400 gm arasında (yani ortalamadan artı eksi k = 2 SDs açıklıkta) olması oranının (3/4)den daha küçük veya (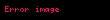
Örneğinde de görüldüğü gibi bu eşitsizlik tipik olarak gevşek sınırlar ortaya çıkartmaktadır Fakat bilinmektedir ki Çebişev'in eşitsizliği ortaya çıkan sınırlar fazla değişemez. Örneğin herhangi bir k ≥ 1, için σ = 1/k olan bir örnek için sınırlar tamamıyla tarif edilmiştir:
Bu dağılım için,
olur. Bu dağılımın bir doğrusal dönüşümü olan herhangi bir dağılım için de aynen uygulanır. Eşitsizlik verilen dağılımın doğrusal dönüşümü olmayan herhangi bir dağılım için aynen uygulanır.
Ölçme teorisi ile ifadesi
(X, Σ, μ) bir ölçme uzayı olsun ve f ise X üzerinde tanımlanan bir genişletilmiş gerçek değerli ölçülebilir fonksiyon olsun. O zaman, herhangi bir t>0 gerçek sayısı için
olur. Daha genel olarak, eğer g, f açıklığı içinde, negatif-olmayan genişletilmiş gerçek değerli ölçülebilir fonksiyon olsun; o zaman
Eğer g(t) ifadesini şöyle tanımlarsak
ve ƒ yerine |ƒ| ele alırsak, daha önce verdiğimiz ifade ortaya çıkar.
Kaynakça
- ^ Bu eşitsizlik ilk defa Fransız "Jules-Irenaeus Bienayme" tarafından 1853 yılında yayınlanmıştır ve birkaç yıl sonra bağımsız olarak Rus "Pafnutiy Çebışov" tarafından yeniden keşfedilmiştir.
- A. Papoulis (1991), Probability, Random Variables, and Stochastic Processes, 3. ed. McGraw-Hill. . pp. 113–114. (İngilizce)
- Geoffrey Grimmett ve D. Stirzaker (2001), Probability and Random Processes, 3. ed. Oxford. . Bölüm 7.3. (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami ve istatistik bilim dallarinda Cebisev in esitsizligi veya Bienayme Cebisev in esitsizligi ozellikle olasilik ve daha nadiren gercek veri setleri icin bir teori sonucu olarak kullanilir Cebisev esitligi veya Cebisev in esitsizligi olasilik teorisi ve istatistik alanlarinda kullanilan bir esitsizliktir Cebisev esitligi bir rassal degiskenin ne kadar yayildigi hakkinda bilgi saglar Bu esitsizligin onemi herhangi bir orneklem verisi veya olasilik dagilimi icin veri degerlerinin hemen tumu nun ortalama degerine yakin oldugunu saglamasindandir Daha matematiksel bir ifade ile bir veri veya olasilik dagilimi degerlerinin 1 k2 oranindan daha buyuk olmayan oraninin ortalamadan arti ve eksi k standart sapma acikligi disinda bulunamayacagini bildirir Bu esitsizligin genis bir kapsami vardir zira sadece ortalama ve standart sapma verilirse diger her turlu niteligi hic bilinmeyen veri veya olasilik dagilimlarina uygulanabilir Esitsizligin ifade edilme sekilleriOlasilik kavramlari ile ifade Beklenen degeri m ve sonsuz olmayan varyansi s2 olan bir rassal degisken olan X degiskenini ele alalim O zaman herhangi bir gercel sayi olan k gt 0 icin Pr X m ks 1k2 displaystyle Pr left X mu right geq k sigma leq frac 1 k 2 olur Burada sadece k gt 1 kosuluna uyan degerler kullanisli bilgi saglamaktadir Bunun diger esit bir sekilde ifade edilmesi soyle olur Pr X m a s2a2 displaystyle Pr left X mu right geq alpha leq frac sigma 2 alpha 2 Ornek olarak k 2 degerini alirsak degerlerin asgari yarisinin su aciklik icinde bulundugunu bu esitsizlige gore kabul ederiz m 2 s m 2 s Sadece ortalamasi ve standart sapmasi bilinen ve her turlu diger nitelikleri hic bilinmeyen dagilim veya verilere uygulandigi icin ortaya cikan sonuc dagilimi daha tam olarak bilinen veri dagilimlardan ortaya cikarabilecegimiz sonuclardan daha fena sinirlar seklinde olmaktadir Ornegin elle yapilan dolum ortalama olarak 1 000 gram agirlik vermektedir ve dolum agirliginin standart dagilimi da 200 gramdir O zaman bu tip bir dolum agirligini 600 ile 1400 gm arasinda yani ortalamadan arti eksi k 2 SDs aciklikta olmasi oraninin 3 4 den daha kucuk veya 1 k2 1 4 displaystyle 1 k 2 1 4 den daha buyuk olamayacagi Cebisev in esitsizligi dolayisiyla bilinir Fakat bu bir dolum agirliginin dagiliminin normal dagilim oldugunu bilirsek o zaman dolumlardan 75 inin 770 ile 1230 gm arasinda oldugu bilinir Gorulmektedir ki ekstra bilgi verilen sinirlari daha da sikilastirmaktadir Orneginde de goruldugu gibi bu esitsizlik tipik olarak gevsek sinirlar ortaya cikartmaktadir Fakat bilinmektedir ki Cebisev in esitsizligi ortaya cikan sinirlar fazla degisemez Ornegin herhangi bir k 1 icin s 1 k olan bir ornek icin sinirlar tamamiyla tarif edilmistir Pr X 1 12k2 Pr X 0 1 1k2 Pr X 1 12k2 displaystyle begin aligned amp Pr X 1 frac 1 2k 2 amp Pr X 0 1 frac 1 k 2 amp Pr X 1 frac 1 2k 2 end aligned Bu dagilim icin Pr X m ks 1k2 displaystyle mathrm Pr left left X mu right geq k sigma right frac 1 k 2 olur Bu dagilimin bir dogrusal donusumu olan herhangi bir dagilim icin de aynen uygulanir Esitsizlik verilen dagilimin dogrusal donusumu olmayan herhangi bir dagilim icin aynen uygulanir Olcme teorisi ile ifadesi X S m bir olcme uzayi olsun ve f ise X uzerinde tanimlanan bir genisletilmis gercek degerli olculebilir fonksiyon olsun O zaman herhangi bir t gt 0 gercek sayisi icin m x X f x t 1t2 Xf2dm displaystyle mu x in X f x geq t leq 1 over t 2 int X f 2 d mu olur Daha genel olarak eger g f acikligi icinde negatif olmayan genisletilmis gercek degerli olculebilir fonksiyon olsun o zaman m x X f x t 1g t Xg fdm displaystyle mu x in X f x geq t leq 1 over g t int X g circ f d mu Eger g t ifadesini soyle tanimlarsak g t t2eger t 00diger halde displaystyle g t begin cases t 2 amp mbox eger t geq 0 0 amp mbox diger halde end cases ve ƒ yerine ƒ ele alirsak daha once verdigimiz ifade ortaya cikar Kaynakca Bu esitsizlik ilk defa Fransiz Jules Irenaeus Bienayme tarafindan 1853 yilinda yayinlanmistir ve birkac yil sonra bagimsiz olarak Rus Pafnutiy Cebisov tarafindan yeniden kesfedilmistir A Papoulis 1991 Probability Random Variables and Stochastic Processes 3 ed McGraw Hill ISBN 0 07 100870 5 pp 113 114 Ingilizce Geoffrey Grimmett ve D Stirzaker 2001 Probability and Random Processes 3 ed Oxford ISBN 0 19 857222 0 Bolum 7 3 Ingilizce
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans