Varyans

Olasılık kuramı ve istatistik bilim dallarında varyans bir rassal değişken, bir olasılık dağılımı veya örneklem için , mümkün bütün değerlerin beklenen değer veya ortalamadan uzaklıklarının karelerinin ortalaması şeklinde bulunan bir ölçüdür. Ortalama bir dağılımın merkezsel konum noktasını bulmaya çalışırken, varyans değerlerin ne ölçekte veya ne derecede yaygın olduklarını tanımlamayı hedef alır. Varyans için orijinal değişkenin biriminin karesidir. Varyansın karekökü standart sapma olarak adlandırılır; bunun ölçme birimi orijinal değişkenle aynı birimde olur ve bu nedenle daha kolayca yorumlanabilir.

Bir reel sayı hâlinde olan rassal değişkenin varyansı o rassal değişkenin ikinci merkezsel momenti ve aynı zamanda ikinci kümülantı olur. Eğer varyans değeri var ise, ortalama değeri de vardır. Ama bunun aksi doğru değildir.

Tanımlama

Formüller

Eğer beklenen değer varsa, bir olasılık dağılımı için varyans dağılımın kendi ortalamasından sapmasının karesinin beklenen değeridir. Varyans kavramı dağılıma ait her bir değerin dağılımın ortalamasından ne kadar uzak olduğuyla ilgilidir. Varyans söz konusu sapmaların ortalama değerini ölçmektedir.

X değişkeninin beklenen değeri μ = E(X) olmak üzere, varyans şöyle tanımlanır:

${\displaystyle \operatorname {var} (X)=\operatorname {E} ((X-\mu )^{2}).}$

Matematik notasyon kullanılarak bir rassal değişken X için varyans ya Var(X) ya ${\displaystyle \scriptstyle \sigma _{X}^{2}}$ ya da daha basitçe σ² olarak gösterilir..

Bu tanımlama, eğer beklenen değer varsa, hem hem hem de karışık değişkenler için genel olarak doğrudur. Bu tanımdan ve beklenen değerlerin doğrusal olma niteliğinden varyans için şu formül çıkartılabilir:

${\displaystyle {}\operatorname {Var} (X)=\operatorname {E} (X^{2}-2\,X\,\operatorname {E} (X)+(\operatorname {E} (X))^{2}),}$

${\displaystyle {}=\operatorname {E} (X^{2})-2(\operatorname {E} (X))^{2}+(\operatorname {E} (X))^{2},}$

${\displaystyle {}=\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}.}$

Buna hesaplama formülü adı da verilir. Bu formüle göre

Varyans, karelerin ortalaması eksi ortalamanın karesine eşittir.

Bir X için, x değerleri olasılığa eşit olan olasılık kütle fonksiyonu bulunur; yani x₁↦p₁, ..., x_n↦p_n, olur. Bu halde aralıklı olasılık dağılımları için varyans şöyle de ifade edilebilir:

${\displaystyle \operatorname {Var} (X)=\sigma ^{2}=\sum _{i=1}^{n}p_{i}{\left[x_{i}-\operatorname {E} (X)\right]}^{2}=\sum _{i=1}^{n}p_{i}(x_{i}-\mu )^{2}=\sum _{i=1}^{n}x_{i}^{2}p_{i}-{[\operatorname {E} (X)]}^{2}}$

Buna göre varyans Xin kendi ortalamasından beklenen değeri olur. Daha basit bir ifade ile

Aralıklı rassal değişken için, varyans her bir veri noktasının veri ortalamasından uzaklıklarının karelerinin ortalamasıdır; yani ortalama sapma kareleridir.

Bir X için beklenen değer E(X) operatörü yerine olasılık yoğunluk fonksiyonu yani ${\displaystyle f(x)}$i kapsayan ve entegrasyon gereken formül konulursa, varyans şu şekilde ifade edilebilir:

${\displaystyle \operatorname {Var} (X)=\sigma ^{2}=\int _{-\infty }^{\infty }{\left[x-\operatorname {E} (X)\right]}^{2}f(x)\mathrm {d} x=\int _{-\infty }^{\infty }x^{2}f(x)\mathrm {d} x-{[\operatorname {E} (X)]}^{2}}$,

Ancak bazı olasılık dağılımları (örnegin Cauchy dağılımı) için beklenen değer anlamsızdır ve bu halde varyans da anlamlı değildir. Diğer bazı olasılık dağılımlarında ise beklenen değer bulunmakla beraber sonlu sayılı bir varyans bulunamaz, çünkü sürekli değişkenler için varyans değeri bulmak için gereken entegral yakınsama göstermez (örneğin Pareto dağılımı).

Örnekler

Varyans; verilerin aritmetik ortalamadan sapmalarının karelerinin aritmetik ortalaması olduğuna göre,

2,2,3,5,3 serisinin varyansı şu şekilde bulunur;

1) Verilerin aritmetik ortalaması (A.O) hesaplanır.

${\displaystyle \operatorname {A} .O={\frac {(2+2+3+5+3)}{5}}=3}$

2) 1. maddedeki ortalamadan, verilerin sapmalarının karelerinin aritmetik ortalaması alınarak varyans bulunur.

${\displaystyle \operatorname {\frac {[(2-3)^{2}+(2-3)^{2}+(3-3)^{2}+(5-3)^{2}+(3-3)^{2}]}{5}} ={\frac {6}{5}}}$

Örneğin 1: Tablo ile verilmiş bir aralıklı deneysel dağılım

Bu örnekte bir X rastlantı değişkeninin i=1,2,3 için aldığı değerler ve X in bu değerleri alması olasılığı bir tablo olarak verilmiştir.

i	1	2	3
xi	-1	1	2
P(xi)	0,5	0,3	0,2

Beklenen değer şöyle hesaplanır:

${\displaystyle \operatorname {E} (X)=-1\cdot 0{,}5+1\cdot 0{,}3+2\cdot 0{,}2=0{,}2}$

Genel formülle, varyans şöyle bulunur:

${\displaystyle \operatorname {Var} (X)=(-1-0{,}2)^{2}\cdot 0{,}5+(1-0{,}2)^{2}\cdot 0{,}3+(2-0{,}2)^{2}\cdot 0{,}2=1{,}56}$

Hesaplama formülu ile ise varyans şöyle hesaplanır ve aynı sonuç verir:

${\displaystyle \operatorname {Var} (X)=(-1)^{2}\cdot 0{,}5+1^{2}\cdot 0{,}3+2^{2}\cdot 0{,}2-0{,}2^{2}=1{,}56.}$

Örneğin 2: Olasılık yoğunluk fonksiyonu verilmiş bir sürekli dağılım

Sürekli rassal değişken X için olasılık yoğunluk fonksiyonu şöyle verilmiştir:

${\displaystyle f(x)={\begin{cases}{\frac {1}{x}}&{\mbox{ eger }}1\leq x\leq e\\0&{\mbox{ digerleri }}\end{cases}}}$

Beklenen değer E(X) şöyle hesaplanır:

${\displaystyle \operatorname {E} (X)=\int _{1}^{e}x\cdot {\frac {1}{x}}dx=e-1}$

Varyans değeri Var(X) şöyle bulunur:

${\displaystyle \operatorname {Var} (X)}$	${\displaystyle =\int _{-\infty }^{\infty }x^{2}\cdot f(x)dx-(\operatorname {E} (X))^{2}=\int _{1}^{e}x^{2}\cdot {\frac {1}{x}}dx-(e-1)^{2}}$
	${\displaystyle \qquad =\left[{\frac {x^{2}}{2}}\right]_{1}^{e}-(e-1)^{2}={\frac {e^{2}}{2}}-{\frac {1}{2}}-(e-1)^{2}\approx 0{,}242}$

Anakütle varyansı ve örneklem varyansı

Teorik olasılık kuramı incelemeleri için varyans: ${\displaystyle \operatorname {var} (X)=\operatorname {E} (X^{2})-\operatorname {E} (X)^{2}}$ formülü kullanılarak tanımlanır.

Sonlu bir anakütlenin varyansı aşağıdaki şekilde gösterilir:

${\displaystyle \sigma ^{2}=\sum _{i=1}^{N}\left(x_{i}-{\overline {x}}\right)^{2}\,\Pr(x_{i}),}$. Bu özel bir varyans tanımı olarak sonlu anakütlelere özgü bir tanımdır.

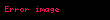
Örneklem varyansı ise şu şekilde tanımlanmaktadır:

${\displaystyle \sigma ^{2}={\frac {1}{N}}\sum _{i=1}^{N}\left(y_{i}-{\overline {y}}\right)^{2},}$

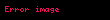
Örneklem varyansı, anakütle varyansının yansız bir kestirmicisidir. İspatı ise aşağıdaki şekilde gösterilir:

${\displaystyle \operatorname {E} \{s^{2}\}=\operatorname {E} \left\{{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}\right\}}$

${\displaystyle ={\frac {1}{n-1}}\sum _{i=1}^{n}\operatorname {E} \left\{\left(x_{i}-{\overline {x}}\right)^{2}\right\}}$

${\displaystyle ={\frac {1}{n-1}}\sum _{i=1}^{n}\operatorname {E} \left\{\left((x_{i}-\mu )-({\overline {x}}-\mu )\right)^{2}\right\}}$

${\displaystyle ={\frac {1}{n-1}}\sum _{i=1}^{n}\operatorname {E} \left\{(x_{i}-\mu )^{2}\right\}-2\operatorname {E} \left\{(x_{i}-\mu )({\overline {x}}-\mu )\right\}+\operatorname {E} \left\{({\overline {x}}-\mu )^{2}\right\}}$

${\displaystyle ={\frac {1}{n-1}}\sum _{i=1}^{n}\sigma ^{2}-2\left({\frac {1}{n}}\sum _{j=1}^{n}\operatorname {E} \left\{(x_{i}-\mu )(x_{j}-\mu )\right\}\right)+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\sum _{k=1}^{n}\operatorname {E} \left\{(x_{j}-\mu )(x_{k}-\mu )\right\}}$

${\displaystyle ={\frac {1}{n-1}}\sum _{i=1}^{n}\sigma ^{2}-{\frac {2\sigma ^{2}}{n}}+{\frac {\sigma ^{2}}{n}}}$

${\displaystyle ={\frac {1}{n-1}}\sum _{i=1}^{n}{\frac {(n-1)\sigma ^{2}}{n}}}$

${\displaystyle ={\frac {(n-1)\sigma ^{2}}{n-1}}=\sigma ^{2}}$

Bu özellikten faydalanılarak örneklem varyansının hesaplanması ile anakütle varyansına ilişkin kestirimlerde bulunulabilir. Bu durumda örneklemin rastsal bir örneklem olması önemlidir. Aksi takdirde örnekleme dayalı kestirimler sağlıklı sonuçlar vermeyecektir.

Varyansın biçimsel özellikleri

Varyansın şu özellikleri bulunmaktadır:

Aralarında korelasyon bulunmayan değişkenlerin toplamı için varyans

Varyansin diğer istatistiksel yayılım ölçülerine kıyasla tercihli olarak kullanılmasına nedenlerden birisi, birbirleri arasında korelasyon olmayan rassal değişkenlerin toplamının (veya farkının) varyansının, her bir rassal değişkenin tek başına olan varyanslarının toplamına (veya farkına) eşit olmasıdır; yani

${\displaystyle \operatorname {Var} {\Big (}\sum _{i=1}^{n}X_{i}{\Big )}=\sum _{i=1}^{n}\operatorname {Var} (X_{i}).}$

Bu öneri çok kere korelasyon yerine daha güçlü bir ilişki olan değişkenlerin bağımsızlığı şartı kullanılarak verilir, ama korelasyon ilişkisi de yeterlidir.

Bu nedenle eğer değişkenlerin varyansları tüm ayni ise (yani hepsi σ² ise), hemen bu formüle göre bunların ortalamasının varyansının şu ifade

${\displaystyle \operatorname {Var} {\Big (}\sum _{i=1}^{n}X_{i}{\Big )}=\sum _{i=1}^{n}\operatorname {Var} (X_{i}).}$

olduğu görülür; çünkü n ile bölme bir doğrusal dönüşümdür.

Bu gerçek, merkezsel limit teoremi içinde özellikle kullanılan, örneklem ortalamasının belirler.

Aralarında korelasyon bulunan değişkenlerin toplamının varyansı

Genel olarak, değişkenler birbirleriyle aralarında korelasyon gösteriyorlarsa, toplamlarının varyansı kovaryanslarının toplamı olur:

${\displaystyle \operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)=\sum _{i=1}^{n}\sum _{j=1}^{n}\operatorname {Kov} (X_{i},X_{j}).}$

Burada Kov kovaryanstır ve eğer herhangi bir rassal değişken bağımsız ise, bu değişkenle diğer değişkenler arasında bulunan her kovaryans değeri 0 olur. Verilen formül toplamın varyansının toplamı yapan parçaların kovaryans matrisinin bütün elemanlarına eşit olduğunu göstermektedir. Bu formül ölçüsü kavramını geliştirmek için de kullanılır.

Eğer değişkenlerin hep birbirine eğit varyansları, yani σ², varsa ve ayrı ayrı değişkenler arasındaki korelasyonların ortalama değeri ρ ise, bu halde varyansların ortalaması şöyle ifade edilir:

${\displaystyle \operatorname {Var} ({\overline {X}})={\frac {\sigma ^{2}}{n}}+{\frac {n-1}{n}}\rho \sigma ^{2}.}$

Bu formüle göre ortalamanın varyansı korelasyonlar ortalaması ile birlikte artış gösterir.

Bunun yanında, eğer değişkenler için varyans 1 değerde ise (örneğin değişken değerleri standardize edilmişlerse) o halde bu formül daha da basitleştirilip şu sekli alır:

${\displaystyle \operatorname {Var} ({\overline {X}})={\frac {1}{n}}+{\frac {n-1}{n}}\rho .}$

Bu formul klasik sinama teorisinde için kullanılır. Eğer korelasyonlar sabit kalırlarsa veya aynı şekilde yakınsama gösterirlerse, bu ifade, n limitte sonsuz değere yakınsama gösterdikçe, ρ değerine yakınsama gösterir. Bunun bir sonucuna göre, eşit korelasyonları olan veya yakınsama gösteren ortalama korelasyonu olan standardize edilmiş değişkenler için ortalamanın varyansı şöyle ifade edilebilir:

${\displaystyle \lim _{n\to \infty }\operatorname {Var} ({\overline {X}})=\rho .}$

Buna göre büyük sayıda standardize edilmiş değişkenlerin ortalamasının varyansı, yaklaşık olarak bunların ortalama korelasyonuna eşittir.

Bu formul diğer bir sonuç da ortaya çıkartır. Büyük sayılar yasası örneklem ortalamasının anakütle ortalamasına yakınsama göstereceğini önermesine rağmen, bu formülden açıktır ki, birbirine korelasyonu olan değişkenler bulunuyorsa örneklem ortalaması anakütle ortalamasına yakınsama göstermez.

Değişkenlerin ağırlıklı toplamının varyansı

Varyansın parçalara ayrılması

Varyans için hesaplama formülü

hemen doğrudan doğruya beklenen değerlerin doğrusallarından ve yukarıda verilen tanımlamadan ortaya çıkar\;

${\displaystyle {}\operatorname {Var} (X)=\operatorname {E} (X^{2}-2\,X\,\operatorname {E} (X)+(\operatorname {E} (X))^{2}),}$

${\displaystyle {}=\operatorname {E} (X^{2})-2(\operatorname {E} (X))^{2}+(\operatorname {E} (X))^{2},}$

${\displaystyle {}=\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}.}$

Bu çok zaman pratikte varyans hesaplaması için kullanılır. Fakat eğer denklemin iki kısmının değerleri birbirine eşit veya çok yakınsa numerik yaklaşımlama hatasından etkilenip yanlış değerler verebilir.

Karakteristik özellik

Bir rassal değişkenin ikinci momentinin minimum değeri bu moment, rassal değişkenin ortalaması etrafında alınınca ortaya çıkar; yani

${\displaystyle \mathrm {argmin} _{m}\,\mathrm {E} ((X-m)^{2})=\mathrm {E} (X)\,}$,

Bunun aksi olarak, eğer sürekli bir fonksiyon olan ${\displaystyle \varphi }$ tüm X rassal değişkenleri için

${\displaystyle \mathrm {argmin} _{m}\,\mathrm {E} (\varphi (X-m))=\mathrm {E} (X)\,}$

koşulunu sağlıyorsa, o halde mutlaka ${\displaystyle \varphi (x)=ax^{2}+b}$ (a > 0) şeklinde bir fonksiyon olması gerekmektedir. Bu koşul çoklu boyutlu hallerde de geçerlidir.

Ayrıca bakınız

• Standart sapma

Kaynakça

1. ^ Kaynak: A. Kagan and L. A. Shepp, "Why the variance?", Statistics and Probability Letters, C. 38, No 4, 1998, say. 329–333. (İngilizce)

Dış kaynaklar

• Spiegel, Murray R ve Stephens, Larry J. (Tr.Çev.: Çelebioğlu, Salih) (2013) İstatistik, İstanbul: Nobel Akademik Yayıncılık