Coulomb yasası ya da Coulomb’un ters kare yasası, bir fizik yasasıdır. Elektrik yüklü tanecikler arasındaki elektrostatiği tanımlar. Bu yasa 1785'te Fransız fizikçi Charles Augustin de Coulomb tarafından yayınlanmıştır ve klasik elektromanyetizmadaki önemli bir gelişmedir. Coulomb yasası Gauss yasasından ve vice versa(bahsi geçen hadisenin tam tersinin de geçerli olduğunu anlatmak için kullanılır)dan türetilmiştir. Yasa elektromanyetizmin prensibi durumuna gelmiştir.
Tarihçe

Antik Akdeniz toplumlarında, kehribar çubuğunun kedi kürküne sürtüldüğünde tüy gibi hafif nesneleri çektiği bilinirdi. MÖ 600'de Miletli Thales statik elektrik üzerine bir takım gözlemler yaptı. Gördüğü şeyi, sürtünmenin mıknatıs görevi gördüğüne yordu. Buna karşın manyetit gibi minerallerin sürtünmeye ihtiyacı yoktu. Thales, bu çekim olayının manyetik alandan dolayı olduğu konusunda yanılıyordu fakat bilim daha sonra manyetizma ve elektriklenme arasında bir bağlantı olduğunu kanıtladı. Elektrik 17. Yüzyıla kadar bir merak olarak kalmıştır. Ardından William Gilbert adında bir İngiliz bilim insanı, mıknatıs taşını kehribarla sürterek oluşan statik elektrikle ilgili elektrik ve manyetizma hakkında araştırmalar yaptı ve bilime Latince bir kelime kazandırdı: electricus. Electricus küçük objelerin sürtündükten sonra birbirini çekme özelliği anlamına geliyordu. Bu kelime İngilizcede electric ve electricity kelimelerini çağrıştırıyordu ve Thomas Browne’ nin 1646’da kurulmuş olan Pseudodoxia Epidemica’sının ilk baskısında görülmüştü. 18. Yüzyılın ilk araştırmacıları, elektriksel kuvvetin yerçekim kuvveti olayında olduğu gibi(ters kare yasası) uzaklıkla azaldığını saptamışlardır. Elektrikle yüklenmiş olan küreler üzerinde yapılan deneylere dayanarak, İngiliz bilim insanı Joseph Priestley ise elektriksel kuvvetin ters kare yasasına uyduğunu ileri süren ilk kişiydi. Fakat bu konunun detaylarına inemedi.

1769’da İskoç fizikçi , yüklü iki cismin birbirini itmesi olayının aynı işaretli yüklerle olduğunu deneylerinde gözlemlediğini duyurdu. 1770'lerin başında İngiliz bilim insanı Henry Cavendish, yüklü iki cismin arasındaki kuvvetin bağlı olduğu yük ve uzaklık olgusunu keşfetmişti fakat bu keşfi hiçbir yazılı kaynakta yer almamıştı. Sonunda 1785'te Fransız fizikçi Charles-Augustin de Coulomb, elektrik ve manyetizma hakkında yazdığı ilk üç raporunda bu yasanın kendi yasası olduğunu belirtti. Yayınlanan bu raporlar elektromanyetizmanın temeli sayılmıştır. Charles-Augustin de Coulomb yüklü cisim arasında itme ya da çekmeyi saptamak için burulma terazisini kullanmıştır. Daha sonra noktasal iki yükün arasındaki elektriksel kuvvetin yükle doğru, uzaklığın karesiyle ters orantılı olduğunu saptamıştır.
Yasa
Coulomb yasası der ki:
- İki noktasal yükün arasındaki elektrostatik kuvvet yüklerin skaler çarpımıyla doğru, aralarındaki uzaklığın karesiyle ters orantılıdır .
- Bu iki cismin yüklerinin işaretleri eğer aynı ise(pozitif-pozitif gibi) birbirlerini iterler, eğer farklıysa birbirlerini çekerler .

Coulomb yasası aynı zamanda basit bir matematik eşitliği gösterir.
ve




Birimler
Elektromanyetik teori açıklanırken genellikle Uluslararası Birimler Sistemi kullanılır. Kuvvet Newton (birim) ile ölçülür, yük coulomb ile ve uzaklık metre birimiyle ölçülür. Coulomb sabiti 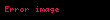

Elektrik alanı

Elektrik alanı bir vektör alanıdır. Coulomb kuvveti, uzaydaki her test yükü ile bağdaştırılır. Daha basitçe, elektrik alanı basit bir noktasal yük kaynağı üretilir. Coulomb kuvvetinin büyüklüğü ve yönü 
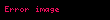



.
Coulomb sabiti
Coulomb sabiti Coulomb yasasında bir orantı faktörü olarak yer almaktadır ayrıca elektrikle ilgili birçok formülde yer almaktadır. 
Yasanın geçerli olması için koşullar
Coulomb yasasının geçerli olabilmesi için iki koşul gerekmektedir.
- Yükler, noktasal yük olmalıdır.
- Yükler birbirlerine göre hareketsiz olmak zorundadır.

 iki notasal yük
iki notasal yük  ve
ve  arasındaki uzaklık ve yüke bağlıdır. Aynı işaretliler birbirini iter, farklı işaretliler birbirini çeker.
arasındaki uzaklık ve yüke bağlıdır. Aynı işaretliler birbirini iter, farklı işaretliler birbirini çeker.Skaler formu
Skaler formu demek, kuvvetin sadece büyüklüğünü bulmaya yöneliktir yani yönü hesaba katılmamaktadır. Sadece büyüklüğü ve işaretiyle ilgilenildiğinde 

Vektör formu

Vektör olan 





Ayrık yükler sistemi
Üst üste gelim ilkesi(örtüşüm ilkesi) Coulomb yasasın içerdiği yük sayısını istenilen sayıda olmasına izin vermektedir. Yüklü cisimler nedeniyle oluşan herhangi bir yük üzerindeki kuvvet, basitçe diğer yükler üzerine etki eden kuvvetlerin vektörel toplamı ile bulunur. Bulunan kuvvet toplamı elektrik alanına paraleldir. Boşluktaki ayrık sistem 







Sürekli yük dağılımı
Bu konuda doğrusal üst üste gelim ilkesi kullanılır. Sürekli yük dağılımında, integral kullanılır. Çünkü sonsuz küçük sayıdaki parça noktasal yük 



.
Alansal yük dağılımında (paralel kondansatörler için ideal yaklaşımdır), 

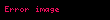
Hacimsel yük dağılımında (mesela hacimsel bir metal kütlede), 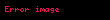

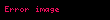
Boşlukta 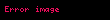

Coulomb yasasını doğrulamaya yönelik basit deney

Coulomb yasasını basit bir deneyle doğrulamak mümkündür. İki küçük küre düşünelim. Kütlesi 




|
| (1 ) |
Ve
|
| (2) |
Eşitlik (1), eşitlik (2)’ye bölündüğünde:
|
| (3) |

|
| (Coulomb Yasası) |
Yani:
|
| (4) |
Eğer yüklerden birisinin yükünü boşaltırsak ve yüklü olan diğer cisimle biribirine değdirirsek 
|
| (5) |

Eşitlik (4), eşitlik (5)’e bölündüğünde:
|
| (6) |
Uygulamada, açıların ölçülmesi zordur. Eğer halatları boyları yeteri kadar uzun olursa, açı aşağıdaki yaklaşımlardaki sonuç gibi küçük olacaktır:
|
| (7) |
Eşitlik (6) kullanılarak daha basit bir sonuç elde edilecektir:
|
| (8) |
Sonsuz küçük sürattaki yayılmanın geçici delili
2012’nin sonunda, 'nin deneycileri, elektron demeti ile algıçlar arasındaki kuvvetin yayılmasında gecikme olmadığını gösterdi. Deney sonucun doğruluğunun kanıtlanması halen beklenmesine rağmen, Aberasyon Coulomb yasasında geçerli olmadığını gösterdi.
Elektrostatik yaklaşım
Coulomb yasasının geçerli olma koşulları, yüklerin hareketsiz kalması ve çok yavaş hareket etmeleridir. Bu koşullar elektrostatik yaklaşım olarak bilinir. Hareket yer aldığı zaman, iki yükün oluşturduğu kuvveti manyetik alan değiştirir.
Atomik kuvvet
Coulomb yasası, atomun çekirdeğindeki pozitif yük ile elektronlardaki negatif yük arasındaki kuvveti de tanımlamaktadır. Bu yasa genel olarak, molekülleri oluşturan atomlar arasındaki kuvvet, sıvı ile katı formundaki maddeleri oluşturan atomlar ve moleküller arasındaki kuvveti açıklar. İyonlar arasındaki uzaklık arttıkça, çekim enerjisi sıfıra yaklaşır. Farklı işaretli yüklerin büyüklükleri arttıkça enerji artar.
Ayrıca bakınız
Kaynakça
- ^ a b Stewart, Joseph (2001). Intermediate Electromagnetic Theory. World Scientific. s. 50. ISBN
- ^ Simpson, Brian (2003). Electrical Stimulation and the Relief of Pain. Elsevier Health Sciences. ss. 6-7. ISBN
- ^ Baigrie, Brian (2006). Electricity and Magnetism: A Historical Perspective. Greenwood Press. ss. 7-8. ISBN
- ^ Chalmers, Gordon (1937). "The Lodestone and the Understanding of Matter in Seventeenth Century England". Philosophy of Science. 4 (1). ss. 75-95. doi:10.1086/286445
- ^ Schofield, Robert E. (1997). The Enlightenment of Joseph Priestley: A Study of his Life and Work from 1733 to 1773. University Park: Pennsylvania State University Press. ss. 144-56. ISBN .
- ^ Priestley, Joseph (1767). The History and Present State of Electricity, with Original Experiments. Londra. s. 732.
May we not infer from this experiment, that the attraction of electricity is subject to the same laws with that of gravitation, and is therefore according to the squares of the distances; since it is easily demonstrated, that were the earth in the form of a shell, a body in the inside of it would not be attracted to one side more than another?
- ^ Elliott, Robert S. (1999). Electromagnetics: History, Theory, and Applications. ISBN . 10 Mart 2014 tarihinde kaynağından . Erişim tarihi: 12 Haziran 2014.
- ^ Robison, John (1822). Murray, John (Ed.). A System of Mechanical Philosophy. 4. Londra.
On page 68 8 Şubat 2015 tarihinde Wayback Machine sitesinde ., the author states that in 1769 he announced his findings regarding the force between spheres of like charge. On page 73 1 Aralık 2016 tarihinde Wayback Machine sitesinde ., the author states the force between spheres of like charge varies as x-2.06:
When making experiments with charged spheres of opposite charge the results were similar, as stated on page 73 1 Aralık 2016 tarihinde Wayback Machine sitesinde .:The result of the whole was, that the mutual repulsion of two spheres, electrified positively or negatively, was very nearly in the inverse proportion of the squares of the distances of their centres, or rather in a proportion somewhat greater, approaching to x-2.06.
Nonetheless, on page 74 1 Aralık 2016 tarihinde Wayback Machine sitesinde . the author infers that the actual action is related exactly to the inverse duplicate of the distance:When the experiments were repeated with balls having opposite electricities, and which therefore attracted each other, the results were not altogether so regular and a few irregularities amounted to 1/6 of the whole; but these anomalies were as often on one side of the medium as on the other. This series of experiments gave a result which deviated as little as the former (or rather less) from the inverse duplicate ratio of the distances; but the deviation was in defect as the other was in excess.
On page 75 1 Aralık 2016 tarihinde Wayback Machine sitesinde ., the authour compares the electric and gravitational forces:We therefore think that it may be concluded, that the action between two spheres is exactly in the inverse duplicate ratio of the distance of their centres, and that this difference between the observed attractions and repulsions is owing to some unperceived cause in the form of the experiment.
Therefore we may conclude, that the law of electric attraction and repulsion is similar to that of gravitation, and that each of those forces diminishes in the same proportion that the square of the distance between the particles increases.
- ^ Maxwell, James Clerk, (Ed.) (1967). "Experiments on Electricity: Experimental determination of the law of electric force.". The Electrical Researches of the Honourable Henry Cavendish... (1.1özgünyıl=1879 bas.). Cambridge, England: Cambridge University Press. ss. 104-113.
On pages 111 and 112 the author states:We may therefore conclude that the electric attraction and repulsion must be inversely as some power of the distance between that of the 2 + 1/50 th and that of the 2 - 1/50 th, and there is no reason to think that it differs at all from the inverse duplicate ratio.
- ^ a b In -- Coulomb (1785a) "Premier mémoire sur l’électricité et le magnétisme," 22 Nisan 2014 tarihinde Wayback Machine sitesinde . Histoire de l’Académie Royale des Sciences, pages 569-577 -- Coulomb studied the repulsive force between bodies having electrical charges of the same sign:
Page 574 : Il résulte donc de ces trois essais, que l'action répulsive que les deux balles électrifées de la même nature d'électricité exercent l'une sur l'autre, suit la raison inverse du carré des distances.
In -- Coulomb (1785b) "Second mémoire sur l’électricité et le magnétisme," 1 Ocak 2014 tarihinde Wayback Machine sitesinde . Histoire de l’Académie Royale des Sciences, pages 578-611. -- Coulomb showed that oppositely charged bodies obey an inverse-square law of attraction.Translation : It follows therefore from these three tests, that the repulsive force that the two balls --[that were] electrified with the same kind of electricity -- exert on each other, follows the inverse proportion of the square of the distance.
- ^ Coulomb's law 13 Nisan 2019 tarihinde Wayback Machine sitesinde ., Hyperphysics
- ^ a b c Coulomb's law 9 Temmuz 2015 tarihinde Wayback Machine sitesinde ., University of Texas
- ^ Charged rods 10 Ekim 2014 tarihinde Wayback Machine sitesinde ., PhysicsLab.org
- ^ Calcaterra, A.; de Sangro, R.; Finocchiaro, G.; Patteri, P.; Piccolo, M.; Pizzella, G. (2012). "Measuring Propagation Speed of Coulomb Fields". arXiv:1211.2913 $2.
Ek kaynaklar
- Coulomb, Charles Augustin (1788) [1785]. "Premier mémoire sur l'électricité et le magnétisme". Histoire de l’Académie Royale des Sciences. Imprimerie Royale. ss. 569-577.
- Coulomb, Charles Augustin (1788) [1785]. "Second mémoire sur l'électricité et le magnétisme". Histoire de l’Académie Royale des Sciences. Imprimerie Royale. ss. 578-611.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3.3 yayıncı=Prentice Hall bas.). ISBN .
- Tipler, Paul A.; Mosca, Gene (2008). Physics for Scientists and Engineers (6.6 yayıncı=W. H. Freeman and Company bas.). New York. ISBN . LCCN 2007010418.
- Young, Hugh D.; Freedman, Roger A. Sears and Zemansky's University Physics : With Modern Physics (13.13 yıl = 2010 bas.). Addison-Wesley (Pearson). ISBN .
Dış bağlantılar
- Coulomb's Law14 Mayıs 2017 tarihinde Wayback Machine sitesinde . on Project PHYSNET14 Mayıs 2017 tarihinde Wayback Machine sitesinde .
- Electricity and the Atom21 Şubat 2009 tarihinde Wayback Machine sitesinde .-a chapter from an online textbook
- A maze game for teaching Coulomb's Law 13 Ekim 2014 tarihinde Wayback Machine sitesinde .-a game created by the Molecular Workbench software
- Electric Charges, Polarization, Electric Force, Coulomb's Law14 Mart 2009 tarihinde Wayback Machine sitesinde . Walter Lewin, 8.02 Electricity and Magnetism, Spring 2002: Lecture 1 (video). MIT OpenCourseWare. License: Creative Commons Attribution-Noncommercial-Share Alike.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Coulomb yasasi ya da Coulomb un ters kare yasasi bir fizik yasasidir Elektrik yuklu tanecikler arasindaki elektrostatigi tanimlar Bu yasa 1785 te Fransiz fizikci Charles Augustin de Coulomb tarafindan yayinlanmistir ve klasik elektromanyetizmadaki onemli bir gelismedir Coulomb yasasi Gauss yasasindan ve vice versa bahsi gecen hadisenin tam tersinin de gecerli oldugunu anlatmak icin kullanilir dan turetilmistir Yasa elektromanyetizmin prensibi durumuna gelmistir TarihceCharles Augustin de Coulomb Antik Akdeniz toplumlarinda kehribar cubugunun kedi kurkune surtuldugunde tuy gibi hafif nesneleri cektigi bilinirdi MO 600 de Miletli Thales statik elektrik uzerine bir takim gozlemler yapti Gordugu seyi surtunmenin miknatis gorevi gordugune yordu Buna karsin manyetit gibi minerallerin surtunmeye ihtiyaci yoktu Thales bu cekim olayinin manyetik alandan dolayi oldugu konusunda yaniliyordu fakat bilim daha sonra manyetizma ve elektriklenme arasinda bir baglanti oldugunu kanitladi Elektrik 17 Yuzyila kadar bir merak olarak kalmistir Ardindan William Gilbert adinda bir Ingiliz bilim insani miknatis tasini kehribarla surterek olusan statik elektrikle ilgili elektrik ve manyetizma hakkinda arastirmalar yapti ve bilime Latince bir kelime kazandirdi electricus Electricus kucuk objelerin surtundukten sonra birbirini cekme ozelligi anlamina geliyordu Bu kelime Ingilizcede electric ve electricity kelimelerini cagristiriyordu ve Thomas Browne nin 1646 da kurulmus olan Pseudodoxia Epidemica sinin ilk baskisinda gorulmustu 18 Yuzyilin ilk arastirmacilari elektriksel kuvvetin yercekim kuvveti olayinda oldugu gibi ters kare yasasi uzaklikla azaldigini saptamislardir Elektrikle yuklenmis olan kureler uzerinde yapilan deneylere dayanarak Ingiliz bilim insani Joseph Priestley ise elektriksel kuvvetin ters kare yasasina uydugunu ileri suren ilk kisiydi Fakat bu konunun detaylarina inemedi Coulomb un burulma terazisi 1769 da Iskoc fizikci yuklu iki cismin birbirini itmesi olayinin ayni isaretli yuklerle oldugunu deneylerinde gozlemledigini duyurdu 1770 lerin basinda Ingiliz bilim insani Henry Cavendish yuklu iki cismin arasindaki kuvvetin bagli oldugu yuk ve uzaklik olgusunu kesfetmisti fakat bu kesfi hicbir yazili kaynakta yer almamisti Sonunda 1785 te Fransiz fizikci Charles Augustin de Coulomb elektrik ve manyetizma hakkinda yazdigi ilk uc raporunda bu yasanin kendi yasasi oldugunu belirtti Yayinlanan bu raporlar elektromanyetizmanin temeli sayilmistir Charles Augustin de Coulomb yuklu cisim arasinda itme ya da cekmeyi saptamak icin burulma terazisini kullanmistir Daha sonra noktasal iki yukun arasindaki elektriksel kuvvetin yukle dogru uzakligin karesiyle ters orantili oldugunu saptamistir YasaCoulomb yasasi der ki Iki noktasal yukun arasindaki elektrostatik kuvvet yuklerin skaler carpimiyla dogru aralarindaki uzakligin karesiyle ters orantilidir Bu iki cismin yuklerinin isaretleri eger ayni ise pozitif pozitif gibi birbirlerini iterler eger farkliysa birbirlerini cekerler A graphical representation of Coulomb s law Coulomb yasasi ayni zamanda basit bir matematik esitligi gosterir F ke q1q2 r2 displaystyle mathbf F k e q 1 q 2 over r 2 qquad ve F1 keq1q2 r21 2r 21 displaystyle qquad mathbf F 1 k e frac q 1 q 2 mathbf r 21 2 mathbf hat r 21 qquad ke displaystyle k e Coulomb sabitidir ke 8 9875517873681764 109 N m2 C 2 displaystyle k e 8 987 551 787 368 176 4 times 10 9 mathrm N cdot m 2 cdot C 2 q1 displaystyle q 1 ve q2 displaystyle q 2 yuk buyuklukleridir r displaystyle r skalerdir ve yuklerin arasindaki uzakliktir r21 r1 r2 displaystyle boldsymbol r 21 boldsymbol r 1 r 2 vektorel olarak yuklerin arasindaki uzakliktir ve r 21 r21 r21 displaystyle boldsymbol hat r 21 boldsymbol r 21 boldsymbol r 21 F1 displaystyle mathbf F 1 kuvvetini bularak q2 displaystyle q 2 tarafindan uygulanan q1 displaystyle q 1 uzerindeki kuvveti bulmus oluruz Eger r12 displaystyle mathbf r 12 kullanilmis olsa o zaman da q2 displaystyle q 2 uzerindeki kuvvet bulunmus olunurdu Bu kural Newton un ucuncu yasasi icin de kullanilmaktadir F2 F1 displaystyle mathbf F 2 mathbf F 1 Birimler Elektromanyetik teori aciklanirken genellikle Uluslararasi Birimler Sistemi kullanilir Kuvvet Newton birim ile olculur yuk coulomb ile ve uzaklik metre birimiyle olculur Coulomb sabiti ke 1 4pe0e displaystyle k e 1 4 pi varepsilon 0 varepsilon ile gosterilir e0 displaystyle varepsilon 0 yalitkanlik sabitidir ve birimi C2 m 2 N 1 Ve e displaystyle varepsilon bagil yalitkanlik sabitidir Elektrik alanin birimi ise birim metredeki voltdur Elektrik alani Iki cisimin yuklerinin isaretleri eger ayni ise birbirlerini iterler eger farkliysa birbirlerini cekerler Elektrik alani bir vektor alanidir Coulomb kuvveti uzaydaki her test yuku ile bagdastirilir Daha basitce elektrik alani basit bir noktasal yuk kaynagi uretilir Coulomb kuvvetinin buyuklugu ve yonu F displaystyle boldsymbol F qt displaystyle q t test yuku uzerindeki E displaystyle boldsymbol E elektrik alanina bagli olarak F qtE displaystyle boldsymbol F q t boldsymbol E esitligi ile bulunur Elektrik alani cizgileri duz cizgilerdir ve pozitif yuklu cisimde cismin merkezinden disari dogru iken negatif yuklu cismde cizgiler disaridan cismin merkezine dogrudur Elektrik alani E displaystyle boldsymbol E Coulomb yasasindan turetilir Boslukta bir test yuku ve noktasal yuk kaynagi secildiginde olusan elektrik alani noktasal yuk kaynagi tarafindan olusur ve formuluze edilmis sekli ise E 14pe0 q r2 displaystyle boldsymbol E 1 over 4 pi varepsilon 0 q over r 2 Coulomb sabiti Coulomb sabiti Coulomb yasasinda bir oranti faktoru olarak yer almaktadir ayrica elektrikle ilgili bircok formulde yer almaktadir ke displaystyle k e ile gosterilir Ayni zamanda elektrik kuvveti sabiti ya da elektrostatik sabiti diye de anilmaktadir Coulomb sabitinin tam degeri ke 14pe0 c02m04p c02 10 7 H m 1 8 9875517873681764 109 N m2 C 2 displaystyle begin aligned k e amp frac 1 4 pi varepsilon 0 frac c 0 2 mu 0 4 pi c 0 2 times 10 7 mathrm H cdot m 1 amp 8 987 551 787 368 176 4 times 10 9 mathrm N cdot m 2 cdot C 2 end aligned Yasanin gecerli olmasi icin kosullar Coulomb yasasinin gecerli olabilmesi icin iki kosul gerekmektedir Yukler noktasal yuk olmalidir Yukler birbirlerine gore hareketsiz olmak zorundadir Kuvvetin mutlak degeri F displaystyle boldsymbol F iki notasal yuk q displaystyle q ve Q displaystyle Q arasindaki uzaklik ve yuke baglidir Ayni isaretliler birbirini iter farkli isaretliler birbirini ceker Skaler formuSkaler formu demek kuvvetin sadece buyuklugunu bulmaya yoneliktir yani yonu hesaba katilmamaktadir Sadece buyuklugu ve isaretiyle ilgilenildiginde F displaystyle boldsymbol F kuvvetinin q1 displaystyle q 1 ve q2 displaystyle q 2 uzerindeki anlik etkisi F ke q1q2 r2 displaystyle boldsymbol F k e q 1 q 2 over r 2 r displaystyle r aradaki uzaklik ke displaystyle k e Coulomb sabitidir q1q2 displaystyle q 1 q 2 carpim sonucu eger pozitif cikarsa birbirlerini itiyor demektir Eger sonuc negatif cikarsa yukler birbirlerini cekiyor demektir Vektor formuCoulomb yasasinin grafiksel gosterimi Vektor olan F1 displaystyle boldsymbol F 1 q1 displaystyle q 1 tarafindan olusur diger vektor F2 displaystyle boldsymbol F 2 de q2 displaystyle q 2 tarafindan olusur q1q2 gt 0 displaystyle q 1 q 2 gt 0 oldugu zaman cisimler birbirini iter resimde oldugu gibi q1q2 lt 0 displaystyle q 1 q 2 lt 0 oldugu zaman ise cisimler birbirini ceker Kuvvetler her zaman birbirine esit olur Coulomb yasasina gore F1 displaystyle boldsymbol F 1 kuvvetinin q1 displaystyle q 1 r1 displaystyle boldsymbol r 1 pozisyonunda ve herhangi bir diger yuk olan q2 displaystyle q 2 r2 displaystyle boldsymbol r 2 pozisyonunda esitligi F1 q1q24pe0 r1 r2 r1 r2 3 q1q24pe0r 21 r21 2 displaystyle boldsymbol F 1 q 1 q 2 over 4 pi varepsilon 0 boldsymbol r 1 r 2 over boldsymbol r 1 r 2 3 q 1 q 2 over 4 pi varepsilon 0 boldsymbol hat r 21 over boldsymbol r 21 2 r21 r1 r2 displaystyle boldsymbol r 21 boldsymbol r 1 r 2 birim vektorleri r 21 r21 r21 displaystyle boldsymbol hat r 21 boldsymbol r 21 boldsymbol r 21 ve e0 displaystyle varepsilon 0 elektrik sabiti Coulomb yasasinin vektor formu birim vektorun yonu ile yasanin basitce skaler tanimi r 21 displaystyle boldsymbol hat r 21 q2 displaystyle q 2 den q1 displaystyle q 1 e paralel cizgidir Eger iki yuk degeri ayni isaret ise yuk carpimlari pozitif olacaktir ve q1 displaystyle q 1 uzerindeki kuvvetin yonu r 21 displaystyle boldsymbol hat r 21 seklinde olacaktir Yukler birbirlerini itecektir Eger yukler zit isaretlelerse q1q2 displaystyle q 1 q 2 skaler carpimi negatif olur ve q1 displaystyle q 1 uzerindeki kuvvetin yonu r 21 displaystyle boldsymbol hat r 21 seklinde olur Yukler birbirini cekecektir Newton un ucuncu yasasina gore elektrostatik kuvvet F2 displaystyle boldsymbol F 2 q2 displaystyle q 2 den olusmaktadir F2 F1 displaystyle boldsymbol F 2 boldsymbol F 1 seklinde gosterilmektedir Ayrik yukler sistemi Ust uste gelim ilkesi ortusum ilkesi Coulomb yasasin icerdigi yuk sayisini istenilen sayida olmasina izin vermektedir Yuklu cisimler nedeniyle olusan herhangi bir yuk uzerindeki kuvvet basitce diger yukler uzerine etki eden kuvvetlerin vektorel toplami ile bulunur Bulunan kuvvet toplami elektrik alanina paraleldir Bosluktaki ayrik sistem N displaystyle N nedeniyle r displaystyle boldsymbol r pozisyonundaki q displaystyle q uzerindeki F displaystyle boldsymbol F kuvveti F r q4pe0 i 1Nqir ri r ri 3 q4pe0 i 1NqiRi Ri 2 displaystyle boldsymbol F r q over 4 pi varepsilon 0 sum i 1 N q i boldsymbol r r i over boldsymbol r r i 3 q over 4 pi varepsilon 0 sum i 1 N q i boldsymbol widehat R i over boldsymbol R i 2 i displaystyle i ninci yukun sirasiyla qi displaystyle q i ve ri displaystyle boldsymbol r i buyukluk ve pozisyonudur Ri displaystyle boldsymbol widehat R i birim vektor ve yonu ise Ri r ri displaystyle boldsymbol R i boldsymbol r boldsymbol r i yonu ise qi displaystyle q i den q displaystyle q a dogrudur Surekli yuk dagilimi Bu konuda dogrusal ust uste gelim ilkesi kullanilir Surekli yuk dagiliminda integral kullanilir Cunku sonsuz kucuk sayidaki parca noktasal yuk dq displaystyle dq gibi davranir ve sonsuz sayidaki noktasal yukun kuvveti de integral yoluyla bulunur Bu yuk dagilimi dogrusal alansal ya da hacimseldir Dogrusal yuk dagiliminda telin icindeki yuk icin ideal yaklasimdir l r displaystyle lambda boldsymbol r bize r displaystyle boldsymbol r konumunda dl displaystyle dl uzunlugunun sonsuz kucuk parcasinda birim uzunluktaki yuk miktarini verir dq l r dl displaystyle dq lambda boldsymbol r dl Alansal yuk dagiliminda paralel kondansatorler icin ideal yaklasimdir s r displaystyle sigma boldsymbol r bize r displaystyle boldsymbol r pozisyonunda dA displaystyle dA sonsuz kucuk alan icinde birim alandaki yuk miktarini verir dq s r dA displaystyle dq sigma boldsymbol r dA Hacimsel yuk dagiliminda mesela hacimsel bir metal kutlede r r displaystyle rho boldsymbol r bize r displaystyle boldsymbol r konumunda dV displaystyle dV sonsuz kucuk hacimde birim hacimdeki yuk miktarini verir dq r r dV displaystyle dq rho boldsymbol r dV Boslukta r displaystyle boldsymbol r konumundaki kucuk test yuku olan q displaystyle q yuk dagilimdaki integral ile bulunur F q 4pe0 dqr r r r 3 displaystyle boldsymbol F q over 4 pi varepsilon 0 int dq boldsymbol r boldsymbol r over boldsymbol r boldsymbol r 3 Coulomb yasasini dogrulamaya yonelik basit deneyCoulomb yasasinu dogrulayan deney Coulomb yasasini basit bir deneyle dogrulamak mumkundur Iki kucuk kure dusunelim Kutlesi m displaystyle m olsun yukleri ise ayni isaretli ve q displaystyle q olsun l displaystyle l uzunlugunda ve kutlesi ihmal edilen iki halattan sarkitilmis olsunlar Her bir kure uzerine etki eden kuvvet uc tanedir bunlar Agirlik mg displaystyle mg halat gerilimi T displaystyle T ve elektrik kuvvvettir F displaystyle boldsymbol F Denge konumundan T sin 81 F1 displaystyle T sin theta 1 F 1 1 Ve T cos 81 mg displaystyle T cos theta 1 mg 2 Esitlik 1 esitlik 2 ye bolundugunde sin 81cos 81 F1mg F1 mgtan 81 displaystyle frac sin theta 1 cos theta 1 frac F 1 mg Rightarrow F 1 mg tan theta 1 3 L1 displaystyle L 1 kureler arasindaki uzaklik F1 displaystyle F 1 kurelerin birbirine yaptigi itme kuvveti F1 q24pϵ0L12 displaystyle F 1 frac q 2 4 pi epsilon 0 L 1 2 Coulomb Yasasi Yani q24pϵ0L12 mgtan 81 displaystyle frac q 2 4 pi epsilon 0 L 1 2 mg tan theta 1 4 Eger yuklerden birisinin yukunu bosaltirsak ve yuklu olan diger cisimle biribirine degdirirsek q 2 displaystyle q 2 her birinin kazanacagi yuk olacaktir Denklik durumuna gore L2 lt L1 displaystyle L 2 lt L 1 olacaktir ve aralarinda itme kuvveti ise F2 q 2 24pϵ0L22 q2 44pϵ0L22 displaystyle F 2 frac q 2 2 4 pi epsilon 0 L 2 2 frac q 2 4 4 pi epsilon 0 L 2 2 5 F2 mg tan 82 displaystyle F 2 mg tan theta 2 oldugunu biliyoruz Ve q244pϵ0L22 mg tan 82 displaystyle frac frac q 2 4 4 pi epsilon 0 L 2 2 mg tan theta 2 Esitlik 4 esitlik 5 e bolundugunde q24pϵ0L12 q2 44pϵ0L22 mgtan 81mgtan 82 4 L2L1 2 tan 81tan 82 displaystyle frac left cfrac q 2 4 pi epsilon 0 L 1 2 right left cfrac q 2 4 4 pi epsilon 0 L 2 2 right frac mg tan theta 1 mg tan theta 2 Longrightarrow 4 left frac L 2 L 1 right 2 frac tan theta 1 tan theta 2 6 Uygulamada acilarin olculmesi zordur Eger halatlari boylari yeteri kadar uzun olursa aci asagidaki yaklasimlardaki sonuc gibi kucuk olacaktir tan 8 sin 8 L2l L2l tan 81tan 82 L12lL22l displaystyle tan theta approx sin theta frac frac L 2 l frac L 2l Longrightarrow frac tan theta 1 tan theta 2 approx frac frac L 1 2l frac L 2 2l 7 Esitlik 6 kullanilarak daha basit bir sonuc elde edilecektir L12lL22l 4 L2L1 2 displaystyle frac frac L 1 2l frac L 2 2l approx 4 left frac L 2 L 1 right 2 Longrightarrow L1L2 4 L2L1 2 L1L2 43 displaystyle frac L 1 L 2 approx 4 left frac L 2 L 1 right 2 Longrightarrow frac L 1 L 2 approx sqrt 3 4 8 Sonsuz kucuk surattaki yayilmanin gecici delili2012 nin sonunda nin deneycileri elektron demeti ile algiclar arasindaki kuvvetin yayilmasinda gecikme olmadigini gosterdi Deney sonucun dogrulugunun kanitlanmasi halen beklenmesine ragmen Aberasyon Coulomb yasasinda gecerli olmadigini gosterdi Elektrostatik yaklasimCoulomb yasasinin gecerli olma kosullari yuklerin hareketsiz kalmasi ve cok yavas hareket etmeleridir Bu kosullar elektrostatik yaklasim olarak bilinir Hareket yer aldigi zaman iki yukun olusturdugu kuvveti manyetik alan degistirir Atomik kuvvet Coulomb yasasi atomun cekirdegindeki pozitif yuk ile elektronlardaki negatif yuk arasindaki kuvveti de tanimlamaktadir Bu yasa genel olarak molekulleri olusturan atomlar arasindaki kuvvet sivi ile kati formundaki maddeleri olusturan atomlar ve molekuller arasindaki kuvveti aciklar Iyonlar arasindaki uzaklik arttikca cekim enerjisi sifira yaklasir Farkli isaretli yuklerin buyuklukleri arttikca enerji artar Ayrica bakinizBiot Savart yasasi Goruntu yuk metodu Elektromanyetik kuvvet Newton un evrensel kutlecekim yasasiKaynakca a b Stewart Joseph 2001 Intermediate Electromagnetic Theory World Scientific s 50 ISBN 981 02 4471 1 Simpson Brian 2003 Electrical Stimulation and the Relief of Pain Elsevier Health Sciences ss 6 7 ISBN 0 444 51258 6 Baigrie Brian 2006 Electricity and Magnetism A Historical Perspective Greenwood Press ss 7 8 ISBN 0 313 33358 0 Chalmers Gordon 1937 The Lodestone and the Understanding of Matter in Seventeenth Century England Philosophy of Science 4 1 ss 75 95 doi 10 1086 286445 Schofield Robert E 1997 The Enlightenment of Joseph Priestley A Study of his Life and Work from 1733 to 1773 University Park Pennsylvania State University Press ss 144 56 ISBN 0 271 01662 0 Priestley Joseph 1767 The History and Present State of Electricity with Original Experiments Londra s 732 May we not infer from this experiment that the attraction of electricity is subject to the same laws with that of gravitation and is therefore according to the squares of the distances since it is easily demonstrated that were the earth in the form of a shell a body in the inside of it would not be attracted to one side more than another Elliott Robert S 1999 Electromagnetics History Theory and Applications ISBN 978 0 7803 5384 8 10 Mart 2014 tarihinde kaynagindan Erisim tarihi 12 Haziran 2014 Robison John 1822 Murray John Ed A System of Mechanical Philosophy 4 Londra On page 68 8 Subat 2015 tarihinde Wayback Machine sitesinde the author states that in 1769 he announced his findings regarding the force between spheres of like charge On page 73 1 Aralik 2016 tarihinde Wayback Machine sitesinde the author states the force between spheres of like charge varies as x 2 06 The result of the whole was that the mutual repulsion of two spheres electrified positively or negatively was very nearly in the inverse proportion of the squares of the distances of their centres or rather in a proportion somewhat greater approaching to x 2 06 When making experiments with charged spheres of opposite charge the results were similar as stated on page 73 1 Aralik 2016 tarihinde Wayback Machine sitesinde When the experiments were repeated with balls having opposite electricities and which therefore attracted each other the results were not altogether so regular and a few irregularities amounted to 1 6 of the whole but these anomalies were as often on one side of the medium as on the other This series of experiments gave a result which deviated as little as the former or rather less from the inverse duplicate ratio of the distances but the deviation was in defect as the other was in excess Nonetheless on page 74 1 Aralik 2016 tarihinde Wayback Machine sitesinde the author infers that the actual action is related exactly to the inverse duplicate of the distance We therefore think that it may be concluded that the action between two spheres is exactly in the inverse duplicate ratio of the distance of their centres and that this difference between the observed attractions and repulsions is owing to some unperceived cause in the form of the experiment On page 75 1 Aralik 2016 tarihinde Wayback Machine sitesinde the authour compares the electric and gravitational forces Therefore we may conclude that the law of electric attraction and repulsion is similar to that of gravitation and that each of those forces diminishes in the same proportion that the square of the distance between the particles increases Maxwell James Clerk Ed 1967 Experiments on Electricity Experimental determination of the law of electric force The Electrical Researches of the Honourable Henry Cavendish 1 1ozgunyil 1879 bas Cambridge England Cambridge University Press ss 104 113 On pages 111 and 112 the author states We may therefore conclude that the electric attraction and repulsion must be inversely as some power of the distance between that of the 2 1 50 th and that of the 2 1 50 th and there is no reason to think that it differs at all from the inverse duplicate ratio a b In Coulomb 1785a Premier memoire sur l electricite et le magnetisme 22 Nisan 2014 tarihinde Wayback Machine sitesinde Histoire de l Academie Royale des Sciences pages 569 577 Coulomb studied the repulsive force between bodies having electrical charges of the same sign Page 574 Il resulte donc de ces trois essais que l action repulsive que les deux balles electrifees de la meme nature d electricite exercent l une sur l autre suit la raison inverse du carre des distances Translation It follows therefore from these three tests that the repulsive force that the two balls that were electrified with the same kind of electricity exert on each other follows the inverse proportion of the square of the distance In Coulomb 1785b Second memoire sur l electricite et le magnetisme 1 Ocak 2014 tarihinde Wayback Machine sitesinde Histoire de l Academie Royale des Sciences pages 578 611 Coulomb showed that oppositely charged bodies obey an inverse square law of attraction Coulomb s law 13 Nisan 2019 tarihinde Wayback Machine sitesinde Hyperphysics a b c Coulomb s law 9 Temmuz 2015 tarihinde Wayback Machine sitesinde University of Texas Charged rods 10 Ekim 2014 tarihinde Wayback Machine sitesinde PhysicsLab org Calcaterra A de Sangro R Finocchiaro G Patteri P Piccolo M Pizzella G 2012 Measuring Propagation Speed of Coulomb Fields arXiv 1211 2913 2 Ek kaynaklarCoulomb Charles Augustin 1788 1785 Premier memoire sur l electricite et le magnetisme Histoire de l Academie Royale des Sciences Imprimerie Royale ss 569 577 Coulomb Charles Augustin 1788 1785 Second memoire sur l electricite et le magnetisme Histoire de l Academie Royale des Sciences Imprimerie Royale ss 578 611 Griffiths David J 1998 Introduction to Electrodynamics 3 3 yayinci Prentice Hall bas ISBN 0 13 805326 X Tipler Paul A Mosca Gene 2008 Physics for Scientists and Engineers 6 6 yayinci W H Freeman and Company bas New York ISBN 0 7167 8964 7 LCCN 2007010418 Young Hugh D Freedman Roger A Sears and Zemansky s University Physics With Modern Physics 13 13 yil 2010 bas Addison Wesley Pearson ISBN 978 0 321 69686 1 Dis baglantilarCoulomb s Law14 Mayis 2017 tarihinde Wayback Machine sitesinde on Project PHYSNET14 Mayis 2017 tarihinde Wayback Machine sitesinde Electricity and the Atom21 Subat 2009 tarihinde Wayback Machine sitesinde a chapter from an online textbook A maze game for teaching Coulomb s Law 13 Ekim 2014 tarihinde Wayback Machine sitesinde a game created by the Molecular Workbench software Electric Charges Polarization Electric Force Coulomb s Law14 Mart 2009 tarihinde Wayback Machine sitesinde Walter Lewin 8 02 Electricity and Magnetism Spring 2002 Lecture 1 video MIT OpenCourseWare License Creative Commons Attribution Noncommercial Share Alike
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans