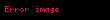Matematikte de Moivre formülü, 18. yüzyıl Fransız matematikçisi Abraham de Moivre anısına isimlendirilmiş ve herhangi bir karmaşık sayı (özellikle herhangi bir gerçel sayı x ve herhangi bir tam sayı n) için şu ifadenin geçerli olduğunu önerir:
Bu formülün önemi (burada önünde i sanal birim ifade ile verilmiş olan) karmaşık sayılar ile trigonometri arasındaki bağlantıyı açıklamasındadır.
Bu formülde "cos x + i sin x" bazen "cis x" olarak kısaltılabilir.
Formülün sol tarafi binom teoremi kullanarak açılıp gerçel kısmına ve sanal kısmına yeni şekil verilirse, cos(nx) ve sin(nx) için yalnızca sin(x) ve cos(x) kullanan uygulamalı matematikde çok önemli ifadeler elde edilir.
Bu formülün diğer bir uygulaması ise De Moivre sayısı adı verilen (yani 1in köklerini) karmaşık sayılar (yani zn = 1 ise zkarmaşık sayıları) ile ifade edilmesini sağlamasıdır
Tarihi olarak başka şekilde ispat edilmekle beraber, de Moivre'in formülü Euler formülünü kullanarak hemen şöyle ispat edilebilir:
ve üstel yasaya göre
O halde Euler formülü ile,
- . olur.
İndüksiyon ile ispat
Üç değişik hal ele alınabilir:
Eğer n > 0 ise, matematiksel tümevarım ile şöyle ilerleyebiliriz.
Eğer n = 1 ise, sonuç açıkça geçerlidir. Hipotezimiz için, sonucun bir tam sayı olan k için geçerli olduğunu varsayalım. Yani varsayımımız şu olsun:
Şimdi n = k + 1 halini ele alalım:

Bundan, eğer sonucun, n = k için geçerli olması halinde, n = k + 1 için de geçerli olduğu anlamına varılır. Öyle ise, matematik endüksiyon prensipine göre, tüm pozitif tam sayılar için (yani n≥1 için) bu sonuç geçerli olur.
Eğer n = 0 ise, 

Eğer n < 0 ise, n = -m olduğu zaman bir pozitif tam sayı m ele alsın. O halde
Böylelikle, teorem nin tüm tam sayı değerleri için geçerlidir.
Kosinus ve sinus için tek tek formüller
Karmaşık sayıların eşitliğini gösterdiği için bu denklemin hem gerçel kısımları hem de sanal kısımları ayrı ayrı birbirine eşit olmalıdır. Eğer x (ve bundan dolayı 

Bu denklemler xin karmaşık değerleri için geçerlidir. Buna neden, her iki tarafın da x in holomorf fonksiyonları olması ve gerçel eksende birbiriyle çakışan bu şekildeki iki fonksiyonun de mutlaka birbiriyle çakışması gereğidir.
Bu denklemlerin örnek ifadeleri olarak 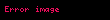
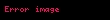



Genelleştirme
Bu formül yukarıda verilen hallerden daha geniş hallerde de geçerlidir. Eğer z ve w karmaşık sayılarsa, o halde
bir olur ve
ise bir çokludeğerli fonksiyon olmaz. Böylece
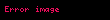

Uygulamalar

Bu formül bir karmaşık sayı için ninci kökleri bulmak için kullanılabilir. Eğer 
O halde
olur. Burada 





Ayrıca bakınız
Dış bağlantılar
- Abramowitzm,M. ve Stegun,I.A. (1964) Handbook of Mathematical Functions, New York, Dover Publications, say. 74 () (İngilizce)
- De Moivre's Theorem for Trig Identities8 Aralık 2008 tarihinde Wayback Machine sitesinde . haz.: Michael Croucher, Wolfram Gösterim Projesi (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte de Moivre formulu 18 yuzyil Fransiz matematikcisi Abraham de Moivre anisina isimlendirilmis ve herhangi bir karmasik sayi ozellikle herhangi bir gercel sayi x ve herhangi bir tam sayi n icin su ifadenin gecerli oldugunu onerir cos x isin x n cos nx isin nx displaystyle left cos x i sin x right n cos left nx right i sin left nx right Bu formulun onemi burada onunde i sanal birim ifade ile verilmis olan karmasik sayilar ile trigonometri arasindaki baglantiyi aciklamasindadir Bu formulde cos x i sin x bazen cis x olarak kisaltilabilir Formulun sol tarafi binom teoremi kullanarak acilip gercel kismina ve sanal kismina yeni sekil verilirse cos nx ve sin nx icin yalnizca sin x ve cos x kullanan uygulamali matematikde cok onemli ifadeler elde edilir Bu formulun diger bir uygulamasi ise De Moivre sayisi adi verilen yani 1in koklerini karmasik sayilar yani zn 1 ise zkarmasik sayilari ile ifade edilmesini saglamasidir Tarihi olarak baska sekilde ispat edilmekle beraber de Moivre in formulu Euler formulunu kullanarak hemen soyle ispat edilebilir eix cos x isin x displaystyle e ix cos x i sin x ve ustel yasaya gore eix n einx displaystyle left e ix right n e inx O halde Euler formulu ile ei nx cos nx isin nx displaystyle e i nx cos nx i sin nx olur Induksiyon ile ispatUc degisik hal ele alinabilir Eger n gt 0 ise matematiksel tumevarim ile soyle ilerleyebiliriz Eger n 1 ise sonuc acikca gecerlidir Hipotezimiz icin sonucun bir tam sayi olan k icin gecerli oldugunu varsayalim Yani varsayimimiz su olsun cos x isin x k cos kx isin kx displaystyle left cos x i sin x right k cos left kx right i sin left kx right Simdi n k 1 halini ele alalim cos x isin x k 1 cos x isin x k cos x isin x cos kx isin kx cos x isin x enduksiyon hipotezine gore cos kx cos x sin kx sin x i cos kx sin x sin kx cos x cos k 1 x isin k 1 x trigonometrik ozdesliklere gore displaystyle begin alignedat 2 left cos x i sin x right k 1 amp left cos x i sin x right k left cos x i sin x right amp left cos left kx right i sin left kx right right left cos x i sin x right amp amp qquad mbox enduksiyon hipotezine gore amp cos left kx right cos x sin left kx right sin x i left cos left kx right sin x sin left kx right cos x right amp cos left left k 1 right x right i sin left left k 1 right x right amp amp qquad mbox trigonometrik ozdesliklere gore end alignedat Bundan eger sonucun n k icin gecerli olmasi halinde n k 1 icin de gecerli oldugu anlamina varilir Oyle ise matematik enduksiyon prensipine gore tum pozitif tam sayilar icin yani n 1 icin bu sonuc gecerli olur Eger n 0 ise cos 0x isin 0x 1 i0 1 displaystyle cos 0x i sin 0x 1 i0 1 oldugu icin ve konvansiyonel olarak z0 1 displaystyle z 0 1 olarak verildigi icin bu formul gecerlidir Eger n lt 0 ise n m oldugu zaman bir pozitif tam sayi m ele alsin O halde cos x isin x n cos x isin x m 1 cos x isin x m 1 cos mx isin mx cos mx isin mx cos mx isin mx cos nx isin nx displaystyle begin aligned left cos x i sin x right n amp left cos x i sin x right m amp frac 1 left cos x i sin x right m amp frac 1 left cos mx i sin mx right amp cos left mx right i sin left mx right amp cos left mx right i sin left mx right amp cos left nx right i sin left nx right end aligned Boylelikle teorem nin tum tam sayi degerleri icin gecerlidir Kosinus ve sinus icin tek tek formullerKarmasik sayilarin esitligini gosterdigi icin bu denklemin hem gercel kisimlari hem de sanal kisimlari ayri ayri birbirine esit olmalidir Eger x ve bundan dolayi cos x displaystyle cos x ve sin x displaystyle sin x gercel sayilar ise o zaman bu kisimlarin ozdeslikleri taraf degistirilerek soyle yazilabilir sin nx k 0n nk cos x k sin x n ksin n k p2cos nx k 0n nk cos x k sin x n kcos n k p2 displaystyle begin aligned sin nx amp sum k 0 n binom n k cos x k sin x n k sin frac n k pi 2 cos nx amp sum k 0 n binom n k cos x k sin x n k cos frac n k pi 2 end aligned Bu denklemler xin karmasik degerleri icin gecerlidir Buna neden her iki tarafin da x in holomorf fonksiyonlari olmasi ve gercel eksende birbiriyle cakisan bu sekildeki iki fonksiyonun de mutlaka birbiriyle cakismasi geregidir Bu denklemlerin ornek ifadeleri olarak n 2 displaystyle n 2 ve n 3 displaystyle n 3 icin su sonuclar cikarilir cos 2x cos x 2 cos x 2 1 2 cos x 2 1sin 2x 2 sin x cos x cos 3x cos x 3 3cos x cos x 2 1 4 cos x 3 3cos xsin 3x 3 cos x 2 sin x sin x 3 3sin x 4 sin x 3 displaystyle begin aligned cos 2x amp left cos x right 2 left left cos x right 2 1 right amp amp 2 left cos x right 2 1 sin 2x amp 2 left sin x right left cos x right cos 3x amp left cos x right 3 3 cos x left left cos x right 2 1 right amp amp 4 left cos x right 3 3 cos x sin 3x amp 3 left cos x right 2 left sin x right left sin x right 3 amp amp 3 sin x 4 left sin x right 3 end aligned cos nx displaystyle cos nx icin formulun sag tarafi gercekte cos x displaystyle cos x degerli olan Tn displaystyle T n ifadesinin n cosx degeridir GenellestirmeBu formul yukarida verilen hallerden daha genis hallerde de gecerlidir Eger z ve w karmasik sayilarsa o halde cos z isin z w displaystyle left cos z i sin z right w bir olur ve cos wz isin wz displaystyle cos wz i sin wz ise bir cokludegerli fonksiyon olmaz Boylece cos wz isin wz displaystyle cos wz i sin wz ifadesi sunun bir parcasidir cos z isin z w displaystyle left cos z i sin z right w Uygulamalar1 in kupkoklerinin karmasik duzlemde gosterimi Bu formul bir karmasik sayi icin ninci kokleri bulmak icin kullanilabilir Eger z displaystyle z bir karmasik sayi ise bu polar koordinatli olarak su sekilde yazilabilir z r cos x isin x displaystyle z r left cos x i sin x right O halde z1n r cos x isin x 1n r1n cos x 2kpn isin x 2kpn displaystyle z frac 1 n left r left cos x i sin x right right frac 1 n r frac 1 n left cos left frac x 2k pi n right i sin left frac x 2k pi n right right olur Burada k displaystyle k tam sayidir z displaystyle z icin n displaystyle n tane degisik kok bulmak icin k displaystyle k nin 0 displaystyle 0 den n 1 displaystyle n 1 e araligini incelemek gerekir Ayrica bakinizAbraham de MoivreDis baglantilarAbramowitzm M ve Stegun I A 1964 Handbook of Mathematical Functions New York Dover Publications say 74 ISBN 0 486 61272 4 Ingilizce De Moivre s Theorem for Trig Identities8 Aralik 2008 tarihinde Wayback Machine sitesinde haz Michael Croucher Wolfram Gosterim Projesi Ingilizce
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State