Değişken değiştirme, İntegral, çarpanlara ayırma, denklemler, , trigonometri ve diferansiyel denklemler başta olmak üzere matematiğin her alanında işlemi basitleştirmek için kullanılan matematiksel bir yöntemdir.
Basit örnek
Sistem aşağıdaki denklemlerden oluşsun.
(Denklem I)
(Denklem II)
Burada, 


Bu sistemin normal çözümü zor değildir. Fakat biraz yorucu olabilir. (Denklem II)'yi şöyle yazabiliriz;
(Denklem III)
Burada 

(Denklem I)'e göre 

veya, (I.çift)
dır. (II.çift)
(I.çift)'i ele alırsak; 


(II.çift)'i ele alırsak; 


Biçimsel tanıtım
















Diğer örnekler
Koordinat dönüşümü
Silindirik koordinat sistemi kullanıldığında bazı sistemlerin çözümü kolaylaşır. Örneğin aşağıdaki denklem;
bazı fiziksel problemlerdeki bir potansiyel enerji fonksiyonu olabilir. Bunun çözümü hemen görülemeyebilir. Fakat aşağıdaki biçime dönüştürülürse;
, burada
olur.
Eğer 






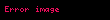


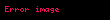
elde edilir.
Şimdi çözüm 



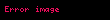


Burada 

Diferansiyel alma
Zincir kuralı, karmaşık diferansiyel denklemleri basitleştirmek için kullanılır. Örneğin aşağıdaki denklemin türevini hesaplamak için;
x2 = u şeklinde değişken değişimi yapılabilir. Ardından zincir kuralı ile:
böylece denklem aşağıdaki biçime dönüşür;
Burada son adım u yerine x2 yazmaktır.
İntegral alma
Zor integraller değişken değiştirerek hesaplanabilir. Burada yerine koyarak integralleme yapılır ve yukarıdaki zincir kuralı] kullanılır. Zor integralleri hesaplamak için Jakobi matris ve determinantı kullanılarak değişken değiştirilir. Böylece denklem koordinat sistemlerine dönüştürülür.
Diferansiyel denklemler
Diferansiyel ve integral alırken kullanılan değişken değiştirme yöntemi kalkülüste öğretilir.
Değişken değiştirmenin çok geniş kullanımı diferansiyel denklemlerde ortaya çıkar. Buradaki bağımsız değişken zincir kuralı kullanılarak değiştirilebilir veya bağımlı değişkenler bazı diferansiyellerin alınması sonucunda değiştirilir. Can alıcı değişiklikler, bağımlı ve bağımsız değişkenlerin, nokta ve bağlantı dönüşümlerinde katıştırılmasıdır. Bu çok karmaşıktır, fakat bir o kadar da rahattır.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Degisken degistirme Integral carpanlara ayirma denklemler trigonometri ve diferansiyel denklemler basta olmak uzere matematigin her alaninda islemi basitlestirmek icin kullanilan matematiksel bir yontemdir Basit ornekSistem asagidaki denklemlerden olussun xy x y 71 displaystyle xy x y 71 Denklem I x2y xy2 880 displaystyle x 2 y xy 2 880 Denklem II Burada x displaystyle x ve y displaystyle y pozitif tam sayi ve x gt y displaystyle x gt y olsun Bu sistemin normal cozumu zor degildir Fakat biraz yorucu olabilir Denklem II yi soyle yazabiliriz xy x y 880 displaystyle xy x y 880 Denklem III Burada s x y displaystyle s x y ve t xy displaystyle t xy degisken degisimlerini uygulayalim Boylece sistemde Denklem I e gore s t 71 displaystyle s t 71 ve Denklem II ye gore st 880 displaystyle st 880 olur Bunun cozumu s t 16 55 displaystyle s t 16 55 veya I cift s t 55 16 displaystyle s t 55 16 dir II cift I cift i ele alirsak x y 16 displaystyle x y 16 ve xy 55 displaystyle xy 55 olur Bu da x y 11 5 displaystyle x y 11 5 i verir II cift i ele alirsak x y 55 displaystyle x y 55 ve xy 16 displaystyle xy 16 olur Bunun cozumu yoktur Sonucta cozum x y 11 5 displaystyle x y 11 5 dir Bicimsel tanitimA displaystyle A B displaystyle B ve F A B displaystyle Phi A rightarrow B aralarinda bir Cr displaystyle C r olsun Burada F displaystyle Phi r displaystyle r kere diferansiyellenebilen A displaystyle A dan B displaystyle B ye bir orten fonksiyon olsun Bunu tersi yine r displaystyle r kere diferansiyellenebilen B displaystyle B den A displaystyle A ya bir fonksiyondur Burada r displaystyle r herhangi bir dogal sayi veya sifir displaystyle infty veya w displaystyle omega analitik fonksiyondur F displaystyle Phi duzenli koordinat sistemi olarak adlandirilir Burada duzenli F displaystyle Phi nin Cr displaystyle C r siz oldugunu ifade eder Diger orneklerKoordinat donusumu Silindirik koordinat sistemi kullanildiginda bazi sistemlerin cozumu kolaylasir Ornegin asagidaki denklem U x y z x2 y2 1 x2x2 y2 0 displaystyle U x y z x 2 y 2 sqrt 1 frac x 2 x 2 y 2 0 bazi fiziksel problemlerdeki bir potansiyel enerji fonksiyonu olabilir Bunun cozumu hemen gorulemeyebilir Fakat asagidaki bicime donusturulurse x y z F r 8 z displaystyle displaystyle x y z Phi r theta z burada F r 8 z rcos 8 rsin 8 z displaystyle displaystyle Phi r theta z r cos theta r sin theta z olur Eger 8 displaystyle theta 2p displaystyle 2 pi periyodunda ornegin 0 2p displaystyle 0 2 pi dondurulurse F displaystyle Phi orten fonksiyon olmaz Bu yuzden F displaystyle Phi ornegin 0 0 2p displaystyle 0 infty times 0 2 pi times infty infty araliginda sinirlanabilir F displaystyle Phi orjinde orten fonksiyon olmasaydi r 0 displaystyle r 0 in nasil hesaba katilmadigina dikkat edin 8 displaystyle theta herhangi bir deger alabilir ve nokta 0 0 z olurdu Ardindan yeni ifadede olusan tum asil degiskenler F displaystyle Phi ile degistirilir ve sin2 x cos2 x 1 displaystyle sin 2 x cos 2 x 1 kullanilir Boylece V r 8 z r21 r2cos2 8r2 r21 cos2 8 r2sin 8 displaystyle V r theta z r 2 sqrt 1 frac r 2 cos 2 theta r 2 r 2 sqrt 1 cos 2 theta r 2 sin theta elde edilir Simdi cozum sin 8 0 displaystyle sin theta 0 icin bulunabilir Cunku 8 0 displaystyle theta 0 veya 8 p displaystyle theta pi dir F displaystyle Phi nin tersi kullanilirsa x 0 displaystyle x not 0 iken y 0 displaystyle y 0 olur y 0 displaystyle y 0 icin fonksiyonun orjin haricinde yok oldugunu gorduk Burada r 0 displaystyle r 0 aldigimiza dikkat edin Her ne kadar asil problemde bir cozum olmazsa bile orjin de bir cozumdu Burada F displaystyle Phi nin orten fonksiyonu cok onemlidir Diferansiyel alma Zincir kurali karmasik diferansiyel denklemleri basitlestirmek icin kullanilir Ornegin asagidaki denklemin turevini hesaplamak icin ddx sin x2 displaystyle frac d dx left sin x 2 right x2 u seklinde degisken degisimi yapilabilir Ardindan zincir kurali ile ddx ddududx ddx u ddu ddx x2 ddu 2xddu displaystyle frac d dx frac d du frac du dx frac d dx left u right frac d du frac d dx left x 2 right frac d du 2x frac d du boylece denklem asagidaki bicime donusur ddx sin x2 2xddu sin u 2xcos x2 displaystyle frac d dx left sin x 2 right 2x frac d du left sin u right 2x cos x 2 Burada son adim u yerine x2 yazmaktir Integral alma Zor integraller degisken degistirerek hesaplanabilir Burada yerine koyarak integralleme yapilir ve yukaridaki zincir kurali kullanilir Zor integralleri hesaplamak icin Jakobi matris ve determinanti kullanilarak degisken degistirilir Boylece denklem koordinat sistemlerine donusturulur Diferansiyel denklemler Diferansiyel ve integral alirken kullanilan degisken degistirme yontemi kalkuluste ogretilir Degisken degistirmenin cok genis kullanimi diferansiyel denklemlerde ortaya cikar Buradaki bagimsiz degisken zincir kurali kullanilarak degistirilebilir veya bagimli degiskenler bazi diferansiyellerin alinmasi sonucunda degistirilir Can alici degisiklikler bagimli ve bagimsiz degiskenlerin nokta ve baglanti donusumlerinde katistirilmasidir Bu cok karmasiktir fakat bir o kadar da rahattir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State











