Vektör hesaplamada, divergence (ıraksama, uzaksama, uzaklaşma) bir vektör alanının kaynak ya da batma noktasından uzaktaki bir noktada genliğini ölçen işleçtir; yani bir vektör alanının uzaksaması işaretli (artı ya da eksi) bir sayıdır. Örneğin ısındıkça genişleyen havanın hızını gösteren bir vektör alanının uzaksaması pozitif olacaktır, çünkü hava genişlemektedir. Eğer hava soğuyup daralıyorsa uzaksama negatif olacaktır. Bu özel örnekte uzaksama yoğunluğun değişiminin ölçüsü olarak düşünülebilir.
Uzaksaması her yerde 0 olan vektör alanına selenoidal denir.
ile gösterilen bir vektör alanın diverjansı fiziksel anlamda en basit olarak alanın akısıyla betimlenebilir. Diverjans, hacim sıfıra giderken, 'in birim hacime düşen akısı olarak tanımlanabilir. Sembolik olarak
burada hacmi saran kapalı yüzeyi belirtmektedir. Diverjans teoremi yardımıyla, diverjansın nabla operatörü () ile 'nin skaler çarpımına eşit olduğu belirlenebilir. Kartezyen koordinatlarda
Genel olarak gibi genel dik koordinatlarda için diverjansın tanımı şöyledir,
burada ilgili koordinatların metrik katsayılarının karekökünü belirtmektedir.
Diverjansın tensör notasyonunda yazılımı,
veya olur.
skaler bir alan, ve de vektörel bir alan olmak üzere, diverjans alma işleminin özellikleri şöyle sıralanabilir:
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Vektor hesaplamada divergence iraksama uzaksama uzaklasma bir vektor alaninin kaynak ya da batma noktasindan uzaktaki bir noktada genligini olcen islectir yani bir vektor alaninin uzaksamasi isaretli arti ya da eksi bir sayidir Ornegin isindikca genisleyen havanin hizini gosteren bir vektor alaninin uzaksamasi pozitif olacaktir cunku hava genislemektedir Eger hava soguyup daraliyorsa uzaksama negatif olacaktir Bu ozel ornekte uzaksama yogunlugun degisiminin olcusu olarak dusunulebilir Uzaksamasi her yerde 0 olan vektor alanina selenoidal denir F x y z displaystyle vec F x y z ile gosterilen bir vektor alanin diverjansi fiziksel anlamda en basit olarak alanin akisiyla betimlenebilir Diverjans hacim sifira giderken F x y z displaystyle vec F x y z in birim hacime dusen akisi olarak tanimlanabilir Sembolik olarak divF limDv 0 SF ds Dv displaystyle mbox div vec F equiv lim Delta v rightarrow 0 frac oint S vec F cdot d vec s Delta v burada S displaystyle scriptstyle S hacmi saran kapali yuzeyi belirtmektedir Diverjans teoremi yardimiyla diverjansin nabla operatoru displaystyle vec nabla ile F displaystyle vec F nin skaler carpimina esit oldugu belirlenebilir Kartezyen koordinatlarda divF F Fx x Fy y Fz z displaystyle mbox div vec F vec nabla cdot vec F frac partial F x partial x frac partial F y partial y frac partial F z partial z Genel olarak u1 u2 u3 displaystyle scriptstyle u 1 u 2 u 3 gibi genel dik koordinatlarda F F1 F2 F3 displaystyle scriptstyle vec F equiv F 1 F 2 F 3 icin diverjansin tanimi soyledir F 1h1h2h3 u1h2h3F1 u2h1h3F2 u3h1h2F3 displaystyle nabla cdot vec F frac 1 h 1 h 2 h 3 left frac partial partial u 1 h 2 h 3 F 1 frac partial partial u 2 h 1 h 3 F 2 frac partial partial u 3 h 1 h 2 F 3 right burada h1 h2 h3 displaystyle scriptstyle h 1 h 2 h 3 ilgili koordinatlarin metrik katsayilarinin karekokunu belirtmektedir Diverjansin tensor notasyonunda yazilimi divF iFi displaystyle mbox div vec F partial i F i veya divF Fi i displaystyle mbox div vec F F i i olur ϕ displaystyle scriptstyle phi skaler bir alan F displaystyle vec F ve G displaystyle vec G de vektorel bir alan olmak uzere diverjans alma isleminin ozellikleri soyle siralanabilir F G F G displaystyle vec nabla cdot vec F vec G vec nabla cdot vec F vec nabla cdot vec G ϕF ϕ F ϕ F displaystyle vec nabla cdot phi vec F vec nabla phi cdot vec F phi vec nabla cdot vec F F G G F F G displaystyle vec nabla cdot vec F times vec G vec G cdot vec nabla times vec F vec F cdot vec nabla times vec G F 0 displaystyle vec nabla cdot vec nabla times F 0
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans
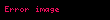


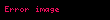




![{\displaystyle \nabla \cdot {\vec {F}}={\frac {1}{h_{1}h_{2}h_{3}}}\left[{\frac {\partial }{\partial u_{1}}}h_{2}h_{3}F_{1}+{\frac {\partial }{\partial u_{2}}}h_{1}h_{3}F_{2}+{\frac {\partial }{\partial u_{3}}}h_{1}h_{2}F_{3}\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5bE56WXdNR1pqWWpWaFltUTRNR1prTXpjek56YzBNVGxqWldNNFpqWTVaRE0wWmpKaU5UYzUuc3Zn.svg)