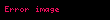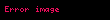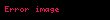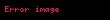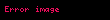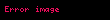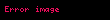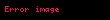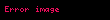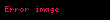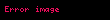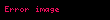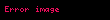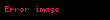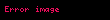Yöney analizinde del işlemcisi, 3 boyutlu Kartezyen koordinatlarda denk gelir ve simgesiyle gösterilir.

tarafından temsil edilir.
Bu işlemci ve yöney (vektör) analizinde büyük kolaylık sağlaması bakımından bir . Temelde kısmi türevdir ve tam türevin çarpanlarından biri olarak düşünülebilir. Bilinen çarpma ve çarpım işlemleriyle yöneysel (vektörel) ve (skaler) alanlara etkir. Ancak bilinen çarpmayla kullanıldığı halde değildir, yazılımda sağ tarafındaki çarpana uygulanır.
Tanım
Del işlemcisi tanımlanır:
O halde, işlemci
olarak tanımlanmış olur. Burada 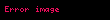
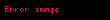
olarak genellenebilir. Buradaki 
Ayrıca gereği nabla işlemcisi tensör olarak:
şeklinde de gösterilebilir. F 'ye etkiyen del işlemcisi virgülle de gösterilebilir:
Burada i=1,2,3 alınır.
Örnekler
- Del işlemcisinin matematikteki çeşitli kullanım alanları: Gradyan, Diverjans, Rotasyonel, Laplasyen.
- Elektromanyetizmada Maxwell Denklemleri del işlemcisiyle ifade edilir.
ve
sırasıyla serbest yüklerin yoğunluğu ve akısı olmak üzere,
- Fizikte korunumlu kuvvetler için potansiyel ifadesi yazılır, bu yüzden korunumlu bir F kuvveti için:
ifadesi geçerlidir ki burada 
Özel görelilikte del işlemcisi
Genelde 3 boyutlu Öklityen uzay ile 4 boyutlu Minkowski uzayı arasındaki fark bu maddede de uygulandığı gibi, Latin harfleriyle (i,j,k,...) gösterilirken yunan harfleriyle (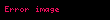
Del işlemcisi genel olarak her yöne ait kısmi türevdir. Einstein'ın Özel Görelilik kuramında 4-del işlemcisi şu şekilde tanımlanır:
Burada 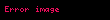
Tensör gösteriminde virgül türev olarak ifade edilir:
Burada 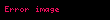
Maxwell denklemlerinin tensör gösterimi
Maxwell Denklemler tensörlerle ifade edilebilir. Kaldı ki bu şekilde dört tane olan denklem sayısı ikiye inmiş olur.
Bu denklemleri daha da sade yazabiliriz:
Buradaki 
Notlar
- ^ Schey, H. M. (1997). Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. New York: Norton. ISBN .
- ^ Miller, Jeff. "Earliest Uses of Symbols of Calculus". 1 Mayıs 2015 tarihinde kaynağından . Erişim tarihi: 5 Ekim 2013.
- ^ Moler, ed., Cleve (26 Ocak 1998). . netlib.org. 12 Mayıs 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Ekim 2013.
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Yoney analizinde del islemcisi 3 boyutlu Kartezyen koordinatlarda denk gelir ve displaystyle nabla simgesiyle gosterilir Del islemcisi tarafindan temsil edilir Bu islemci ve yoney vektor analizinde buyuk kolaylik saglamasi bakimindan bir Temelde kismi turevdir ve tam turevin carpanlarindan biri olarak dusunulebilir Bilinen carpma ve carpim islemleriyle yoneysel vektorel ve skaler alanlara etkir Ancak bilinen carpmayla kullanildigi halde degildir yazilimda sag tarafindaki carpana uygulanir TanimDel islemcisi tanimlanir dF F xdx F ydy F zdz e x F x e y F y e z F z exdx eydy ezdz F dr displaystyle dF frac partial F partial x dx frac partial F partial y dy frac partial F partial z dz left hat e x frac partial F partial x hat e y frac partial F partial y hat e z frac partial F partial z right cdot e x dx e y dy e z dz vec nabla F cdot d vec r dd O halde islemci e x x e y y e z z displaystyle vec nabla hat e x frac partial partial x hat e y frac partial partial y hat e z frac partial partial z dd olarak tanimlanmis olur Burada xi displaystyle partial partial x i islemcisi kismi turev e i displaystyle hat e i ler de i 1 2 3 n boyutlu Oklit uzayinda bu gosterim i 1ne i xi displaystyle vec nabla sum i 1 n hat e i partial over partial x i dd olarak genellenebilir Buradaki ei displaystyle e i ler birim yoneylerdir ve i 1 2 n alinir Ayrica geregi nabla islemcisi tensor olarak i e i xi displaystyle nabla i hat e i frac partial partial x i dd seklinde de gosterilebilir F ye etkiyen del islemcisi virgulle de gosterilebilir iF F xi iF F i displaystyle nabla i F frac partial F partial x i partial i F F i dd Burada i 1 2 3 alinir OrneklerDel islemcisinin matematikteki cesitli kullanim alanlari Gradyan Diverjans Rotasyonel Laplasyen Elektromanyetizmada Maxwell Denklemleri del islemcisiyle ifade edilir rs displaystyle rho s ve J s displaystyle vec J s sirasiyla serbest yuklerin yogunlugu ve akisi olmak uzere D rs displaystyle nabla cdot vec D rho s B 0 displaystyle nabla cdot vec B 0 E B t displaystyle nabla times vec E frac partial vec B partial t H J s D t displaystyle nabla times vec H vec J s frac partial vec D partial t dd Fizikte korunumlu kuvvetler icin potansiyel ifadesi yazilir bu yuzden korunumlu bir F kuvveti icin F F displaystyle vec F nabla Phi dd ifadesi gecerlidir ki burada F displaystyle Phi gondermesi eger F elektrik alan eger F manyetik alan ya da eger F kutlecekim kuvveti ise Dalga denkleminde 2F 1c2 2F 2t 0 displaystyle nabla 2 F frac 1 c 2 frac partial 2 F partial 2 t 0 dd d Alembert Islemcisi 2 x2 2 y2 2 z2 1c2 2 t2 displaystyle square partial 2 over partial x 2 partial 2 over partial y 2 partial 2 over partial z 2 frac 1 c 2 partial 2 over partial t 2 dd Ozel gorelilikte del islemcisiGenelde 3 boyutlu Oklityen uzay ile 4 boyutlu Minkowski uzayi arasindaki fark bu maddede de uygulandigi gibi Latin harfleriyle i j k gosterilirken yunan harfleriyle a b m n displaystyle alpha beta dots mu nu dots gosterilmesi adet olmustur Del islemcisi genel olarak her yone ait kismi turevdir Einstein in Ozel Gorelilik kuraminda 4 del islemcisi su sekilde tanimlanir m ct 1c t x y z displaystyle partial mu frac partial partial ct vec nabla left frac 1 c frac partial partial t frac partial partial x frac partial partial y frac partial partial z right dd Burada m 0 1 2 3 displaystyle mu 0 1 2 3 alinir ve c Tensor gosteriminde virgul turev olarak ifade edilir F xm mF F m displaystyle frac partial F partial x mu partial mu F F mu dd Burada m 0 1 2 3 displaystyle mu 0 1 2 3 alinir Maxwell denklemlerinin tensor gosterimiMaxwell Denklemler tensorlerle ifade edilebilir Kaldi ki bu sekilde dort tane olan denklem sayisi ikiye inmis olur mFmn Jn displaystyle partial mu F mu nu J nu sFmn nFsm mFns 0 displaystyle partial sigma F mu nu partial nu F sigma mu partial mu F nu sigma 0 dd Bu denklemleri daha da sade yazabiliriz Fms m Jn displaystyle F mu sigma mu J nu ϵtmnsFns m 0 displaystyle epsilon tau mu nu sigma F nu sigma mu 0 dd Buradaki ϵdabg displaystyle epsilon delta alpha beta gamma carpani Notlar Schey H M 1997 Div Grad Curl and All That An Informal Text on Vector Calculus New York Norton ISBN 0 393 96997 5 Miller Jeff Earliest Uses of Symbols of Calculus 1 Mayis 2015 tarihinde kaynagindan Erisim tarihi 5 Ekim 2013 Moler ed Cleve 26 Ocak 1998 netlib org 12 Mayis 2012 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Ekim 2013 KB1 bakim Fazladan yazi yazar listesi link Kaynakca
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans