Doğum günü problemi

Olasılık teorisinde, doğum günü problemi veya doğum günü paradoksu, n adet rastgele seçilmiş kişiden oluşan bir grup içindeki bazı çiftlerin doğum gününün aynı olma olasılığını inceler. Güvercin deliği ilkesine göre, kişi sayısı 367’ye ulaştığında (29 Şubat dahil, 366 adet olası doğum günü olduğu için) olasılık %100’e ulaşır fakat, %99,9 olasılığa sadece 70 kişi ile ve %50 olasılığa 23 kişi ile ulaşılır. Bu sonuçlar, yılın her gününün (29 Şubat hariç) eşit derecede olası bir doğum günü olduğu varsayımına dayanır.

Mevcut doğum kayıtları farklı günlerde farklı sayıda insanın doğduğunu gösterir. Bu durumda, %50 eşiğine ulaşmak için gereken insan sayısının 23 veya daha az olduğu söylenebilir. Örneğin, insanların yarısı bir günde ve diğer yarısı başka bir günde doğmuş olsaydı, bu durumda herhangi iki kişinin doğum gününü paylaşma şansı %50 olurdu.

Gruptaki en az iki kişinin aynı doğum gününe sahip olma olasılığının %50’ye ulaşılması için sadece 23 kişilik bir grubun gerektiği şaşırtıcı görünebilir: bu sonuç, bir bireye sabitlenmenin ve onun doğum gününü diğerleriyle karşılaştırmanın aksine doğum günü karşılaştırmasının aslında, olası her bir çift arasında = 23 x 22/2 = 253 karşılaştırma -bir yıl içindeki gün sayısının yarısından (en fazla 183) daha çok- yapılmasıyla daha makul olabilir. Doğum günü problemi kendisiyle mantıksal çelişkili olma anlamda bir “paradoks” değildir, ancak ilk bakışta anlaşılamaz.

Doğum günü probleminin gerçek hayattaki uygulamaları arasında doğum günü saldırısı isimli bir kriptografik saldırı vardır; bu saldırı bu olasılık modelini kullanarak bir özet fonksiyonu için çarpışma bulma karmaşıklığını azaltır ve büyüklüğü belirli bir popülasyonun özetleri arasında bulunan bir özet çarpışmasının yaklaşık riskini hesaplar.

Problemin tarihi bilinmemektedir. W. W. Rouse Ball, bunun ilk olarak Harold Davenport tarafından ele alındığını belirtmiştir (alıntı yok). Ancak, Richard von Mises, bugün doğum günü problemi olarak bilinen şeyin daha eski bir versiyonunu sunmuştur.

En az iki kişinin doğum günü paylaşma olasılığına karşı kişi sayısı

Olasılığın hesaplanması

Problem, n kişiden oluşan bir grup içindeki en az iki kişinin doğum gününün aynı olma olasılığını yaklaşık olarak hesaplamaktır. Basitlik adına, artık yıllar, ikizler, sezonluk veya iş günü değişiklikleri gibi dağılımdaki değişimler göz ardı edilmiştir ve 365 olası doğum gününün hepsinin eşit derecede olası olduğu varsayılmıştır. (Gerçekte doğum günü dağılımları düzenli değildir çünkü tüm tarihler eşit derecede olası değildir, fakat bu düzensizliklerin analiz üzerinde çok az etkisi vardır. Aslında, doğum günlerinin düzenli dağılımı en kötü durumdur.)

Amaç, P(A) ile ifade edilen, odadaki en az iki kişinin doğum gününün aynı olma olasılığını hesaplamaktır. Ancak, P(A’) ile ifade edilen, odadaki hiç kimsenin doğum gününün aynı olmama olasılığını hesaplamak daha kolaydır. Bu durumda, sadece A ve A’ olasılık dahilinde ve ayrık olaylar olduğu için, P(A)=1-P(A’).

P(A)’nın %50’den fazla olması için gereken kişi sayısının en az 23 olduğunu belirten yaygın çözümleri dikkate alarak, aşağıdaki P(A) hesaplamasında örnek olarak 23 kişi kullanılacaktır. Eğer 23 kişi 1’den 23’e kadar numaralandırılırsa, 23 kişinin hepsinin farklı doğum günlerine sahip olması olayı, 2. kişinin 1. kişi ile aynı doğum gününe sahip olmama olayı ile ve 3. kişinin 1. ve 2. kişiyle aynı doğum gününe sahip olmama olayı, vb.; ve son olarak 23. kişinin 1’den 22’ye kadar olan kişilerin hiçbiri ile aynı doğum gününe sahip olmama olayı ile aynıdır. Bu olaylar sırasıyla “Olay 2”, “Olay 3” vb. olarak isimlendirilsin. “Olay 1” olarak ise, 1. kişinin doğum gününe sahip olma olayı, ki bu olayın olasılığı 1’dir, eklenebilir. Bu olayların birleşimi koşullu olasılık kullanılarak hesaplanabilir: Olay 2’nin olasılığı 364/365’tir, çünkü 2. kişinin doğum günü, 1. kişinin doğum günü dışındaki herhangi bir günde olabilir. Benzer şekilde, Olay 2’nin gerçekleştiği göz önüne alındığında, Olay 3’ün olasılığı 363/365’tir, çünkü 3. kişinin doğum günü 1. ve 2. kişinin doğum günleri dışında her gün olabilir. Bu, önceki tüm olayların gerçekleştiği göz önüne alındığında, Olay 23’ün olasılığı 343/365 olana kadar devam eder. Son olarak, koşullu olasılık prensibi, P(A’)’nın bu ayrı olasılıkların çarpımına eşit olduğunu belirtir:

   

${\displaystyle P(A')={\frac {365}{365}}\times {\frac {364}{365}}\times {\frac {363}{365}}\times {\frac {362}{365}}\times \cdots \times {\frac {343}{365}}}$

(1)

    Denklem ( 1 )’in terimleri tek tarafta toplanırsa:

   

${\displaystyle P(A')=\left({\frac {1}{365}}\right)^{23}\times (365\times 364\times 363\times \cdots \times 343)}$

(2)

    Denklem ( 2 ) çözümü P(A′) ≈ 0.492703'ü verir.

Bu nedenle, P(A) ≈ 1 − 0.492703 = 0.507297   (50,7297%).

Bu yöntem n kişiden oluşan bir grup için genelleştirilebilir, p(n) n kişiden en az iki kişinin bir doğum günü paylaşması olasılığıdır. Öncelikle, tüm n doğum günlerinin farklı olma olasılığını, p(n), hesaplamak daha kolaydır. Güvercin yuvası prensibine göre, n>365 ise p(n) sıfırdır. n ≤ 365 ise:

${\displaystyle {\begin{aligned}{\bar {p}}(n)&=1\times \left(1-{\frac {1}{365}}\right)\times \left(1-{\frac {2}{365}}\right)\times \cdots \times \left(1-{\frac {n-1}{365}}\right)\\[6pt]&={\frac {365\times 364\times \cdots \times (365-n+1)}{365^{n}}}\\[6pt]&={\frac {365!}{365^{n}(365-n)!}}={\frac {n!\cdot {\binom {365}{n}}}{365^{n}}}={\frac {_{365}P_{n}}{365^{n}}}\end{aligned}}}$

! faktöriyel operatörü, (365n) binom katsayısı ve _kP_r permütasyonu ifade eder.

Bu denklem, ilk kişinin kimseyle doğum günü paylaşmadığı gerçeğini ifade eder, bununla birlikte, ikinci kişi ilk kişi ile (364/365 ) aynı doğum gününe sahip olamaz, üçüncü kişinin doğum günü ilk iki kişi ile (364/365) ve genel olarak n’inci doğum günü önceki hiçbir n-1 doğum günü ile aynı olamaz.

n kişiden en az ikisinin aynı doğum gününe sahip olma olayı, tüm n doğum günlerinin farklı olması ile tamamlayıcıdır. Bu nedenle, olasılığı

${\displaystyle p(n)=1-{\bar {p}}(n).}$

Aşağıdaki tablo n’in diğer bazı değerleri için olasılıkları göstermektedir (bu tabloda artık yılların varlığı göz ardı edilmiştir ve her doğum gününün eşit derecede olası olduğu varsayılmıştır):

n kişilik bir grupta herhangi iki kişinin doğum günü paylaşmama olasılığı. Düşey ölçek logaritmiktir (aşağı doğru her adım 10²⁰ kat daha az olasıdır)

n	p(n)
1	00.0%
5	02.7%
10	11.7%
20	41.1%
23	50.7%
30	70.6%
40	89.1%
50	97.0%
60	99.4%
70	99.9%
75	99.97%
100	99,99997%
200	99,9999999999999999999999999998%
300	(100 − 6×10^-80)%
350	(100 − 3×10^-129)%
365	(100 − 1,45×10^-155)%
≥ 366	100%

Artık yıllar. Eğer 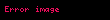${\displaystyle {\bar {p}}(n)}$ formülünde 365 yerine 366 yazarsak, benzer bir hesaplama ile artık yıllar için, bir eşleşme olasılığının %50’den fazla olması için gerekli kişi sayısının 23 olduğunu gösterir; bu durumda eşleşme olasılığı %50.6’dır

Doğum gününü ( red ) ve tamamlayıcı etkinliğini ( blue ) paylaşan en az iki kişinin yaklaşık olasılıklarını gösteren grafikler

1 − e^{−n2⁄₇₃₀} bir yaklaşım 1 − e^{−n2⁄₇₃₀} doğruluğunu gösteren bir grafiktir 1 − e^{−n2⁄₇₃₀} red

Üstel fonksiyonun Taylor serisi açılımı (sabit e ≈ 2,718281828)

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots }$

${\displaystyle |x|\ll 1}$ değerleri için, e^x için birinci dereceden yaklaşım sağlar.

${\displaystyle e^{x}\approx 1+x.}$

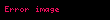
Bu yaklaşımı p(n) için türetilmiş ilk denkleme uygulamak için,

x = −a/365. Böylece,

${\displaystyle e^{-a/365}\approx 1-{\frac {a}{365}}.}$

Bu durumda, a = n − 1 olana kadar p(n) formülündeki a negatif olmayan tam sayılarla değiştirilirse, örneğin, ne a = 1 iken,

${\displaystyle e^{-1/365}\approx 1-{\frac {1}{365}}.}$

p(n) için türetilmiş ilk denklem, şu şekilde yaklaşık olarak bulunabilir:

${\displaystyle {\begin{aligned}{\bar {p}}(n)&\approx 1\cdot e^{-1/365}\cdot e^{-2/365}\cdots e^{-(n-1)/365}\\[6pt]&=e^{-\left.{\big (}1+2+\,\cdots \,+(n-1){\big )}\right/365}\\[6pt]&=e^{-(n(n-1)/2)/365}=e^{-n(n-1)/730}.\end{aligned}}}$

Bu nedenle,

${\displaystyle p(n)=1-{\bar {p}}(n)\approx 1-e^{-n(n-1)/730}.}$

Daha kaba bir yaklaşım şu şekilde verilir

${\displaystyle p(n)\approx 1-e^{-n^{2}/730},}$

ki, grafikte görüldüğü üzere, hala oldukça doğrudur.

Yaklaşıma göre, aynı yöntem herhangi bir sayıda “insan” ve “gün” için de uygulanabilir. Eğer 365 gün yerine d varsa, n kişi varsa ve n ≪ d ise, o zaman yukarıdaki yaklaşımı kullanarak, p(n, d) n kişiden en az iki kişinin, d uygun gün içerisinden aynı doğum gününü paylaşma olasılığını belirtiyor ise, ulaşacağımız sonuç:

${\displaystyle {\begin{aligned}p(n,d)&\approx 1-e^{-n(n-1)/(2d)}\\[6pt]&\approx 1-e^{-n^{2}/(2d)}.\end{aligned}}}$

Basit üssalma

Herhangi iki kişinin aynı doğum gününe sahip olmama olasılığı 364/365’tir. n kişinin olduğu bir odada (n2) = n(n − 1)/2  çift insan, bir başka deyişle (n2) olay vardır. Hiçbir iki kişinin aynı doğum gününü paylaşmama olasılığı, bu olayların bağımsız olduğunu varsaymak ve olasılıklarını beraber çarpmak ile yaklaşık olarak bulunabilir. Kısaca

364/365 kendisi ile (n2) kere çarpılır, bu da:

${\displaystyle {\bar {p}}(n)\approx \left({\frac {364}{365}}\right)^{\binom {n}{2}}.}$

Bu kimsenin aynı doğum gününe sahip olmama olasılığı olduğu için, birinin bir doğum günü paylaşma olasılığı:

${\displaystyle p(n)\approx 1-\left({\frac {364}{365}}\right)^{\binom {n}{2}}.}$

Poisson yaklaşımı

Binom için Poisson yaklaşımının 23 kişilik gruba uygulanmasıyla,

${\displaystyle \operatorname {Poi} \left({\frac {\binom {23}{2}}{365}}\right)=\operatorname {Poi} \left({\frac {253}{365}}\right)\approx \operatorname {Poi} (0.6932)}$

bu yüzden,

${\displaystyle \Pr(X>0)=1-\Pr(X=0)\approx 1-e^{-0.6932}\approx 1-0.499998=0.500002.}$

Sonuç, önceki açıklamalar gibi %50’nin üzerindedir. Bu yaklaşım yukarıdaki 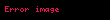${\displaystyle e^{x}\approx 1+x}$ kullanan Taylor açılımı yaklaşımıyla aynıdır.

Kare yaklaşımı

Zihinsel hesaplama için kullanılabilecek iyi bir kural,

${\displaystyle p(n)\approx {\frac {n^{2}}{2m}}}$

ayrıca şu şekilde de yazılabilir

${\displaystyle n\approx {\sqrt {2m\times p(n)}}}$

1/2’den küçük veya 1/2’ye eşit olasılıklar için etkilidir. Bu denklemlerde, m bir yıldaki gün sayısıdır. 

Örneğin, ortak bir doğum günü şansının 1/2 olması için gereken kişi sayısını tahmin etmek için

${\displaystyle n\approx {\sqrt {2\times 365\times {\tfrac {1}{2}}}}={\sqrt {365}}\approx 19}$

Bu da doğru cevap olan 23’ten çok uzak değildir.

Kişi sayısı yaklaşımı

Bu aynı zamanda, eşleşme şansın en az 1/2 olması için gereken kişi sayısı, aşağıdaki formül kullanılarak yaklaşık olarak hesaplanabilir:

${\displaystyle n\approx {\tfrac {1}{2}}+{\sqrt {{\tfrac {1}{4}}+2\times \ln(2)\times 365}}=22.999943.}$

Bu, 1/k olasılığı olan bir olayın, eğer k kere tekrarlanırsa, en az bir kere gerçekleşme şansının 1/2 olacağına dair iyi bir yaklaşımın sonucudur.

Olasılık tablosu

length of hex string	no. of bits (b)	hash space size (2^b)	Number of hashed elements such that probability of at least one hash collision ≥ p
			p = 10^-18	p = 10^-15	p = 10^-12	p = 10^-9	p = 10^-6	p = 0.001	p = 0.01	p = 0.25	p = 0.50	p = 0.75
8	32	4,3×10^9	2	2	2	2.9	93	2,9×10^3	9,3×10^3	5,0×10^4	7,7×10^4	1,1×10^5
(10)	(40)	(1,1×10^12)	2	2	2	47	1,5×10^3	4,7×10^4	1,5×10^5	8,0×10^5	1,2×10^6	1,7×10^6
(12)	(48)	(2,8×10^14)	2	2	24	7,5×10^2	2,4×10^4	7,5×10^5	2,4×10^6	1,3×10^7	2,0×10^7	2,8×10^7
16	64	1,8×10^19	6.1	1,9×10^2	6,1×10^3	1,9×10^5	6,1×10^6	1,9×10^8	6,1×10^8	3,3×10^9	5,1×10^9	7,2×10^9
(24)	(96)	(7,9×10^28)	4,0×10^5	1,3×10^7	4,0×10^8	1,3×10^10	4,0×10^11	1,3×10^13	4,0×10^13	2,1×10^14	3,3×10^14	4,7×10^14
32	128	3,4×10^38	2,6×10^10	8,2×10^11	2,6×10^13	8,2×10^14	2,6×10^16	8,3×10^17	2,6×10^18	1,4×10^19	2,2×10^19	3,1×10^19
(48)	(192)	(6,3×10^57)	1,1×10^20	3,5×10^21	1,1×10^23	3,5×10^24	1,1×10^26	3,5×10^27	1,1×10^28	6,0×10^28	9,3×10^28	1,3×10^29
64	256	1,2×10^77	4,8×10^29	1,5×10^31	4,8×10^32	1,5×10^34	4,8×10^35	1,5×10^37	4,8×10^37	2,6×10^38	4,0×10^38	5,7×10^38
(96)	(384)	(3,9×10^115)	8,9×10^48	2,8×10^50	8,9×10^51	2,8×10^53	8,9×10^54	2,8×10^56	8,9×10^56	4,8×10^57	7,4×10^57	1,0×10^58
128	512	1,3×10^154	1,6×10^68	5,2×10^69	1,6×10^71	5,2×10^72	1,6×10^74	5,2×10^75	1,6×10^76	8,8×10^76	1,4×10^77	1,9×10^77

Bu tabloda açık renkli alanlar, belli bir bit boyutunda verilen özet alanı (satır) belirli çarpışma olasılığını (sütun) başarmak için gereken özet sayısını göstermektedir. Doğum günü benzetmesi kullanılarak: “özet alan boyutu” “uygun günler”e, “çarpışma olasılığı” “ortak doğum günü olasılığı”na ve “gerekli özet elementi sayısı” “bir grup içerisinden gerekli kişi sayısı”na benzemektedir. Bu grafik ayrıca gerekli minimum özet boyutunu (özet üst sınırları ve hata olasılığı verildiğinde) veya çarpışma olasılığını (sabit sayıda özet ve hata olasılığı için) belirlemek için de kullanılabilir.

Karşılaştırma yapılırsa, 10^-18 ile 10^-15, tipik bir sabit diskin bit olarak düzeltilemez hata oranıdır. Teorik olarak, MD5gibi 128-bit özet fonksiyonları, olası çıktıları çok daha fazla olsa bile, yaklaşık 8,2×10¹¹ belgeye kadar bu aralıkta kalmalıdır.

Olasılık üst sınırı ve kişi sayısı alt sınırı

Aşağıdaki argüman Paul Halmos'un bir görüşünden uyarlanmıştır.

Yukarıda belirtildiği gibi, hiçbir iki doğum gününün örtüşmeme olasılığı

${\displaystyle 1-p(n)={\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).}$

Önceki paragraflardaki gibi, p(n) > 1/2’i sağlayan en küçük n değeri ile veya p(n) < 1/2’i sağlayan en küçük n değeri ile ilgilenilmektedir.

1 − x < e−x eşitsizliği kullanılarak, yukarıdaki denklemde 1 − k/365 yerine e−k⁄365 yazıldığında 

${\displaystyle {\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right)<\prod _{k=1}^{n-1}\left(e^{-k/365}\right)=e^{-n(n-1)/730}.}$

Bu nedenle, yukarıdaki denklem yalnızca bir yaklaşım değil, aynı zamanda p(n) için bir üst sınırdır. Eşitsizlik

${\displaystyle e^{-n(n-1)/730}<{\frac {1}{2}}}$

p(n) < 1/2 olduğunu gösterir. n için çözülürse

${\displaystyle n^{2}-n>730\ln 2.}$

Bu durumda, 730 ln 2 yaklaşık olarak 505.997’ye eşittir, ki bu 506’nın çok az altındadır, n² − n değeri n = 23 iken elde edilir. Bu nedenle 23 kişi yeterlidir. Yeri gelmişken, n² − n = 730 ln 2 denkleminin n için çözülmesi, yukarıda bahsedilen Frank H. Mathis’in formülünü yaklaşık olarak verir.

Bu derivasyon sadece, eşit şansa sahip bir doğum günü eşleşmesi sağlamak için en fazla 23 kişiye ihtiyaç duyulduğunu göstermektedir; n’in 22 veya daha az olmasının işe yarama olasılığının ucunu açık bırakmaktadır.

Genelleştirmeler

Genelleştirilmiş doğum günü problemi

Verilen d adet güne sahip bir yılda, genelleştirilmiş doğum günü problemi, rastgele seçilen n kişilik bir grupta bir doğum gününün örtüşme olasılığını en az %50 yapan minimum n(d) sayısını sorar. Başka bir deyişle, n(d) minimum n tam sayısıdır öyle ki,

${\displaystyle 1-\left(1-{\frac {1}{d}}\right)\left(1-{\frac {2}{d}}\right)\cdots \left(1-{\frac {n-1}{d}}\right)\geq {\frac {1}{2}}.}$

Klasik doğum günü problemi bu nedenle, n(365)’in belirlenmesine karşılık gelir. n(d)’nin ilk 99 değeri burada verilmiştir (OEIS'de A033810 dizisi):

d	1–2	3–5	6–9	10–16	17–23	24–32	33–42	43–54	55–68	69–82	83–99
n(d)	2	3	4	5	6	7	8	9	10	11	12

Benzer bir hesaplama, d 341-372 aralığında olduğunda n(d)=23 olduğunu gösterir

n(d) için bir dizi sınır ve formül yayınlanmıştır. Tüm d ≥ 1 için n(d) sayısı aşağıdaki eşitsizliği sağlar:

${\displaystyle {\frac {3-2\ln 2}{6}}<n(d)-{\sqrt {2d\ln 2}}\leq 9-{\sqrt {86\ln 2}}.}$

Bu limitler, n(d) − √2d ln 2 dizisinin aşağıdaki sayıya rastgele yakınlaşması açısından uygundur;

${\displaystyle {\frac {3-2\ln 2}{6}}\approx 0.27,}$

aslında,

${\displaystyle 9-{\sqrt {86\ln 2}}\approx 1.28}$

d = 43 alındığında maksimumdadır. 

Limitler, tüm olayların %99’unda n(d)’nin tam değerini verecek kadar sıkıdır, örneğin n(365) = 23. Genel olarak, bu sınırlardan n(d)’nin daima

${\displaystyle \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil \quad {\text{veya}}\quad \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil +1}$

‘e eşit olduğu görülür; ⌈ · ⌉ tavan fonksiyonunu ifade eder. Formül

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil }$

tüm tamsayı d’lerin %73’ü için geçerlidir. Formül

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}\right\rceil }$

neredeyse tüm d ’ler için, yani asimptotik yoğunluğu 1 olan tam sayı d kümesi için, geçerlidir.

Formül

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}\right\rceil }$

d ≤ 1018 için geçerlidir, ancak bu formüle sonsuz sayıda karşı örnek olduğu tahmin edilir.

Formül

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}-{\frac {2(\ln 2)^{2}}{135d}}\right\rceil }$

d ≤ 1018 için geçerlidir ve bu formülün tüm d değerleri için geçerli olduğu tahmin edilir. 

2 kişiden fazla

Problem, gruptan en az 3/4/5 vb. kişinin aynı doğum gününü paylaşma olasılığının %50’den fazla olması için kaç kişilik bir grubun gerektiğini sormak için genişletilebilir.

İlk birkaç değer şöyledir: 3 kişinin bir doğum günü paylaşma olasılığı>50% - 88 kişi; 4 kişinin bir doğum günü paylaşma olasılığı>50% - 187 kişi. Tüm liste Tam sayı Dizilerinin Çevrimiçi Ansiklopedisi’nin A014088 dizisinde bulunabilir.

Bir çarpışma problemi olarak tahmin

Doğum günü problemi aşağıdaki şekilde genelleştirilebilir:

[1,d] aralığındaki ayrı bir muntazam dağılımdan alınan n rastgele tam sayı verildiğinde, en az iki sayının aynı olma olasılığı, p(n; d) nedir? ( d = 365 olağan doğum günü problemini verir. )

Genel sonuçlar yukarıda verilen aynı argümanlar kullanılarak türetilebilir.

${\displaystyle {\begin{aligned}p(n;d)&={\begin{cases}1-\displaystyle \prod _{k=1}^{n-1}\left(1-{\frac {k}{d}}\right)&n\leq d\\1&n>d\end{cases}}\\[8px]&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\&\approx 1-\left({\frac {d-1}{d}}\right)^{\frac {n(n-1)}{2}}\end{aligned}}}$

Diğer taraftan, eğer n(p; d) en az iki sayının aynı olma olasılığını elde etmek için [1,d]’den alınan rastgele tamsayıların sayısını belirtirse,

${\displaystyle n(p;d)\approx {\sqrt {2d\cdot \ln \left({\frac {1}{1-p}}\right)}}.}$

Daha genel anlamdaki bu doğum günü problemi özet fonksiyonları için geçerlidir: çarpışma almadan önce oluşturulabilecek N - Bit özet sayısı 2^N değil, sadece 2^N⁄₂'dir. Bu, kriptografik karma işlevlerine yapılan doğum günü saldırıları tarafından istismar edilir ve doğum günü saldırıları az sayıda çarpışmanın, tüm pratik amaçlar için, kaçınılmaz olmasının nedenidir.

Doğum günü probleminin arkasında yatan teori Zoe Schnabel istatistikleri adı altında, göllerdeki balık popülasyonunun büyüklüğünü tahmin etmek için kullanılmıştır.

Çoklu tip için genelleştirme

En az bir erkek ve bir kadın arasındaki en az bir ortak doğum günü olasılığının grafiği

Temel problem, tüm denemelerin tek bir “tip” olduğunu kabul eder. Doğum günü problemi, rastgele tip sayısını hesaba katmak için genelleştirilebilir. En basit kapsamda, m erkek ve n kadın olmak üzere iki tip insan vardır ve problem, en az bir erkek ve bir kadın arasındaki ortak doğum günü olasılığını simgeler. (İki erkek veya iki kadın arasındaki ortak doğum günleri sayılmaz.) Burada paylaşılan doğum günlerinin olmama olasılığı

${\displaystyle p_{0}={\frac {1}{d^{m+n}}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(m,i)S_{2}(n,j)\prod _{k=0}^{i+j-1}d-k}$

d = 365 ve S2 ikinci dereceden Stirling sayılarıdır. Dolayısıyla, istenen olasılık 1 − p0’dır. 

Doğum günü probleminin bu değişimi ilginçtir çünkü toplam insan sayısı m + n için tek özgün çözüm yoktur. Örneğin, olağan %50 olasılık değeri, hem 16 erkek ve 16 kadından oluşan 32 üyeli grup için hem de 43 kadın ve 6 erkekten oluşan 49 üyeli grup için gerçekleştirilir.

Notlar

1. ^ In reality, birthdays are not evenly distributed throughout the year; there are more births per day in some seasons than in others, but for the purposes of this problem the distribution is treated as uniform. In particular, many children are born in the summer, especially the months of August and September (for the northern hemisphere) [1], and in the U.S. it has been noted that many children are conceived around the holidays of Christmas and . Also, because hospitals rarely schedule and on the weekend, more people are born between Tuesday and Friday than on weekends; where many of the people share a birth year (e.g. a class in a school), this creates a tendency toward particular dates. In Sweden 9.3% of the population is born in March and 7.3% in November when a uniform distribution would give 8.3% Swedish statistics board. See also:
   • Murphy, Ron. . 26 Mayıs 2001 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Aralık 2011. 
   • Mathers, C D; R S Harris (1983). "Seasonal Distribution of Births in Australia". International Journal of Epidemiology. 12 (3). ss. 326-331. doi:10.1093/ije/12.3.326. (PMID) 6629621. 23 Şubat 2012 tarihinde kaynağından . Erişim tarihi: 27 Aralık 2011. 
   These factors tend to increase the chance of identical birth dates, since a denser subset has more possible pairs (in the extreme case when everyone was born on three days, there would obviously be many identical birthdays). The problem of a non-uniform number of births occurring during each day of the year was first understood by in 1967. A formal proof that the probability of two matching birthdays is least for a uniform distribution of birthdays was given by Bloom Bloom 1973.

Kaynakça

1. ^ ^{a b c} Mario Cortina Borja; John Haigh (September 2007). "The Birthday Problem". Significance. Royal Statistical Society. 4 (3): 124-127. doi:10.1111/j.1740-9713.2007.00246.x . 
2. ^ ^{a b} Frank, P.; Goldstein, S.; Kac, M.; Prager, W.; Szegö, G.; Birkhoff, G., (Ed.) (1964). Selected Papers of Richard von Mises. 2. Providence, Rhode Island: Amer. Math. Soc. ss. 313-334. 
3. ^ J. Michael Steele (2004). The Cauchy‑Schwarz Master Class (İngilizce). Cambridge: Cambridge University Press. ss. 206, 277. ISBN . 16 Mayıs 2013 tarihinde kaynağından . 
4. ^ Mathis, Frank H. (Haziran 1991). "A Generalized Birthday Problem". SIAM Review. 33 (2). ss. 265-270. doi:10.1137/1033051. ISSN 0036-1445. JSTOR 2031144. OCLC 37699182. ^[]
5. ^ Jim Gray, Catharine van Ingen. Empirical Measurements of Disk Failure Rates and Error Rates
6. ^ In his autobiography, Halmos criticized the form in which the birthday paradox is often presented, in terms of numerical computation. He believed that it should be used as an example in the use of more abstract mathematical concepts. He wrote:

   “	The reasoning is based on important tools that all students of mathematics should have ready access to. The birthday problem used to be a splendid illustration of the advantages of pure thought over mechanical manipulation; the inequalities can be obtained in a minute or two, whereas the multiplications would take much longer, and be much more subject to error, whether the instrument is a pencil or an old-fashioned desk computer. What do not yield is understanding, or mathematical facility, or a solid basis for more advanced, generalized theories.	„

7. ^ D. Brink (2012), "A (probably) exact solution to the Birthday Problem", Ramanujan Journal, 27 Ekim 2020 tarihinde kaynağından , erişim tarihi: 24 Mart 2020 
8. ^ Brink 2012, Theorem 2
9. ^ Brink 2012, Theorem 3
10. ^ Brink 2012, Table 3, Conjecture 1
11. ^ . The On-line Encyclopedia of Integer Sequences. OEIS. 1 Eylül 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Şubat 2020. 
12. ^ Suzuki, K.; Tonien, D. (2006). "Birthday Paradox for Multi-collisions". Rhee M.S., Lee B. (Ed.). Lecture Notes in Computer Science, vol 4296. Berlin: Springer. doi:10.1007/11927587_5. Information Security and Cryptology – ICISC 2006. 
13. ^ Z. E. Schnabel (1938) The Estimation of the Total Fish Population of a Lake, 45, 348–352.
14. ^ (2003) Collision Probability Between Sets of Random Variables, Statistics and Probability Letters 64(3), 249–254.

Konuyla iligli yayınlar

• Abramson (1970). "More Birthday Surprises". . 77 (8). ss. 856-858. 
• Bloom (1973). "A Birthday Problem". . 80 (10). ss. 1141-1142. 
• Kemeny, John G.; Snell, J. Laurie; Thompson, Gerald (1957). Introduction to Finite Mathematics (First ed.).
• Klamkin (1967). "Extensions of the Birthday Surprise". Journal of Combinatorial Theory. 3 (3). ss. 279-282. 
• McKinney (1966). "Generalized Birthday Problem". . 73 (4). ss. 385-387. 
• Leila Schneps; Coralie Colmez (12 Mart 2013). Math on Trial (İngilizce). Basic Books (AZ). ISBN . 
• S. M. Blinder (2013). Guide to Essential Math (İngilizce). Elsevier Science Limited. ISBN . 15 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 24 Mart 2020.