Doğrusal olmayan regresyon

Doğrusal olmayan regresyon, istatistik bilimde gözlemi yapılan verilerin bir veya birden fazla bağımsız değişkenin model parametrelerinin doğrusal olmayan bileşiği olan ve bir veya daha çok sayıda bağımsız değişken ihtiva eden bir fonksiyonla modelleştirilmesini içeren bir regresyon (bağlanım) analizi türüdür. Veriler arka-arkaya yapılan yaklaşımlarla kurulan modele uydurularak çözümleme yapılır.

Ayrıntılar için İngilizce Michaelis-Menten kinetics sayfasına bakabilirsiniz.

Genel açıklama

Veriler hiç hatadan arınmış bağımsız değişkenler olan , x ve bunlara bileşik olan gözümlenen bağımlı değişken , y değişkeninden oluşur. Her y ortalama'sı verilmiş bir doğrusal-olmayan fonksiyon f(x,β) olan bir rassal değişken olarak modelleştirilmiştir. bulunabilir ama bunların ele alınması regresyon analizi içeriğinde bulunmaz. Eğer bağımsız değişkenler hatadan arınmamışlarsa, bu daha karmaşık olan kullanılması gerektirecektir ve burada ele alınan yöntem daha basit olup bu fazladan karmaşıklığı ele almamaktadır.

Örneğin, enzim kinetik analizleri için şöyle ifade edilir:

${\displaystyle v={\frac {V_{\max[}{\mbox{S}}]}{K_{m}+[{\mbox{S}}]}}}$

Bu ifade şöyle de yazılabilir:

${\displaystyle f(x,{\boldsymbol {\beta }})={\frac {\beta _{1}x}{\beta _{2}+x}}}$

Bu ifadede ${\displaystyle \beta _{1}}$, ${\displaystyle V_{\max }}$ parametresi; ${\displaystyle \beta _{2}}$, ${\displaystyle K_{m}}$ parametresi ve [S] bağımsız değişken olan x dir. Bu fonksiyon doğrusal olamayan bir fonksiyondur, çünkü ${\displaystyle \beta }$ lerin bir ile ifade edilemezler.

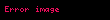
Doğrusal olmayan fonksiyonlara diğer örneğinler , , trigonometrik fonksiyonlar, üstel ifadeler ihtiva eden [[eksponanasyon fonksiyonları, ve fonksiyonlardır. Üstel fonksiyonlar veya logaritmik fonksiyonlar gibi bazı fonksiyonlar dönüşüm kullanılarak doğrusal fonskiyon olarak ifade edilebilirler. Böyle bir dönüşümden sonra standart doğrusal regresyon analizi tatbik edilebilir ama bunun uygulanmasında çok dikkatli bulunmak gerekmektedir.

Genel olarak, doğrusal regresyon'da olduğu gibi en-uygun-olarak yerleştirilme ile tahmin edilmiş parametreler için kapalı-şekilli ifadeler bulunmaz. Çok kere sayısal matematik optimazisyon algoritmalarını kullanarak, optimize edilecek fonksiyon için çoklu yerel maksimum/minimum bulunabilir ve göbal optimiüm bulunsa bile kestirimler ortaya çıkarabilir. Uygulamada bir kareler toplamının global minimum ifadesini bulmaya çalışma sırasında, optimazisyon algorimi ile birlikte parametrelerin kestirim tahminleri kullanılır.

Regresyon istatistikleri

Bu yordamın altında yatan varsayım, modelin şu şekilde bir doğrusal fonksiyonla yaklaşımı yapılabilme imkânı olduğudur

${\displaystyle f(x_{i},{\boldsymbol {\beta }})\approx f^{0}+\sum _{j}J_{ij}\beta _{j}}$o

Burada

${\displaystyle J_{ij}={\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}}$.

Bundan çıkartılan sonuç, en küçük kareler kestrimleri şu formülle verilir:

${\displaystyle {\hat {\boldsymbol {\beta }}}\approx \mathbf {(J^{T}J)^{-1}J^{T}y} .}$

Doğrusal olmayan istatistiklerin hesaplanması da doğrusal regresyon gibi kestirimi yapılır ama formüllerde X yerine J kullanılması gerekir. Doğrusal yaklaşım kullanmak çıkartılan sonucu yanlı olmasına sonuç verir. Bunun için doğrusal olamayan regresyon modelinin kullanılması ile ortaya çıkartılan sonuçların alışılagelenden daha şüpheci bir şekilde kullanılması gerekir.

Alelade ve ağırlıklı en küçük kareler

"En iyi uyan" eğri çok kere karelerinin toplamını minimize edenidir. Buna (alelade) yaklaşımı adı verilir. Fakat, eğer bağımlı değişkenin sabit varyansı bulunmuyorsa, ağırlıklı karesi alınmış artıklar kullanılabilir (bakınız ). İdeal olarak kullanılan her bir ağırlık, bir üstü gözlemi yapılan değerin varyasyonu olması tercih edilmelidir. Ama tekrarlanan hesaplı ağırlıklı en küçük kareler algorıtması kullanılıp her bir hesaplama için ağırlıklar tekrar hesaplanıp değiştirilebilir.

Doğrusallaştırma

Dönüştürme

Bazı doğrusal olmayan regresyon problemleri modelin uygun olan dönüştürmesiyle bir doğrusal çerçeveye geçirtilebilir.

Örneğin, (hataları ele almadan) şu doğrusal olmayan regresyon modelini ele alalım:

${\displaystyle y=ae^{bx}.\,\!}$

Eşitliğin her iki tarafının logaritmaları alınırsa, model şu yeni şekle dönüşür:

${\displaystyle \ln {(y)}=\ln {(a)}+bx,\,\!}$

Bu şekildeki model bilinmeyen katsayılarının kestirimi için bağımlı değişkeni ln(y) ve bağımlı değişkeni x olan bir doğrusal regresyon modelidir ve tekrarlanan optimizasyon yöntemi kullanılması istemeden; doğru doğruya en alelade en küçük kareler regreson yöntemi ile yapılabilir. Fakat doğrusal dönüşüm kullanılmasının çok dikkatle yapılması gerekir. Dönüşümlü modeller için kullanılan vei değerleri başkadır; hatalar bünyesi ve kestirimler üzerinde çıkarımsal sonuçlar da değişik olduğu iyi bilmesi gerekir. Bunlar istenilmeyen sonuçların elde edilmesine yol açabilir. Diğer taraftan, hataların en yüksek kaynağının ne olduğuna bağlı olarak, bir doğrusal dönüşüm hataların normal dağılım göstermesine sonuç olabilir. Bu nedenle bir doğrusal dönüşüm kullanmayı seçmek için modelin karakterlerini iyi bilme gerekir.

analizi için, 1/v ile 1/[S] eksenleri olan bir doğrusal "Lineweaver-Burk" gösterimi, yani

${\displaystyle {\frac {1}{v}}={\frac {1}{V_{\max }}}+{\frac {K_{m}}{V_{\max[}S]}}}$

çok defa kullanılmaktadır. Fakat bu veri hatalarına karşı çok hassaslık gösterir ve [S] bağımsız değişkenin belirli bir açıklığı içinde verileri kullanıp model kurma yanlılığına yol açtığı bilinmektedir. Bu nedenle bu dönüşümün pratikte kullanılması tavsiye edilmemekte ve başka yaklaşımlara kullanılması salık verilmektedir..

Bölümleme

Hardal bitkisinin randımanı ve toprak tuzluluğu

Ana madde:

"Bağımsız değişken" veya "açıklayıcı değişken (diyelim X) bölümlere veya parçalara veya sınıflara bölünebilir ve her bir bölüm için ayrı ayrı uygulanabilir. ile birlikte uygulanan bölümler için regresyon, her bir bölüm için bağımlı değişken veya açıklanan değişken (diyelim Y) için değişik davranış gösterdiğini ortaya çıkaran bir sonuç elde edilebilir.

Yandaki gösterimde X = "toprak tuzluğu" kolza yetiştirilmesinde "ürün randımanına" (Y) ilk önce hiç etki yapmamaktadır. Fakat (kırılma noktası adı verilebilecek) belirli bir kritik veya eşik değer geçilince randıman menfi olarak etkilenmektedir.

Bu gösterim SegReg adlı bir kompüter programı kullanılarak hazırlanmıştır. <reg>SegReg kompüter programı hiç parasız [3] 13 Şubat 2010 tarihinde Wayback Machine sitesinde . adlı websitesinde yüklenebilir.

Dipnotlar

1. ^ R.J.Oosterbaan, 1994, Frequency and Regression Analysis (Sıklık ve Regresyon Analizi) . Kaynak: H.P.Ritzema (ed.), Drainage Principles and Applications, Publ. 16, pp. 175-224, International Institute for Land Reclamation and İmprovement (İLRİ), Wageningen, The Netherlands. . PDF : [1] 22 Temmuz 2011 tarihinde Wayback Machine sitesinde .
2. ^ R.J.Oosterbaan, 2002. Tarımcıların tarlalarında şu çekimi: veri analizi. Uluslararası Toprak Reklamasyonu ve Geliştirilmesi Enstitüsü (İLRİ) Wageningen, Holland. (PDF) : [2] 22 Temmuz 2011 tarihinde Wayback Machine sitesinde .

Ayrıca bakınız

• Regresyon

Dış bağlantılar

• İngilizce Wikiopedia "Nonlienar regression" maddesi:[4] 17 Aralık 2008 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:21.5.2010).