Regresyon analizi, iki ya da daha çok nicel değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Eğer tek bir değişken kullanılarak analiz yapılıyorsa buna tek değişkenli regresyon, birden çok değişken kullanılıyorsa çok değişkenli regresyon analizi olarak isimlendirilir. Regresyon analizi ile değişkenler arasındaki ilişkinin varlığı, eğer ilişki var ise bunun gücü hakkında bilgi edinilebilir. Regresyon terimi için öz Türkçe olarak bağlanım sözcüğü kullanılması teklif edilmiş ise de Türk ekonometriciler arasında bu kullanım yaygın değildir.
Örneğin, bir ziraat mühendisi buğday verimi ve gübre miktarı arasındaki ilişkiyi, bir mühendis, basınç ve sıcaklık, bir ekonomist gelir düzeyi ve tüketim harcamaları, bir eğitimci öğrencilerin devamsızlık gösterdiği gün sayıları ve başarı dereceleri arasındaki ilişkiyi bilmek isteyebilir. Regresyon, iki (ya da daha çok) değişken arasındaki doğrusal ilişkinin fonksiyonel şeklini, biri bağımlı diğeri bağımsız değişken olarak bir doğru denklemi olarak göstermekle kalmaz, değişkenlerden birinin değeri bilindiğinde diğeri hakkında kestirim yapılmasını sağlar. Genellikle bu iki (veya çok) değişkenlerin hepsinin niceliksel ölçekli olması zorunluluğu vardır.
Regresyonda, değişkenlerden biri bağımlı diğerleri bağımsız değişken olmalıdır. Buradaki mantık eşitliğin solunda yer alan değişkenin sağında yer alan değişkenlerden etkilenmesidir. Sağda yer alan değişkenlerse diğer değişkenlerden etkilenmemektedir. Burada etkilenmemek matematiksel anlamda bu değişkenleri bir doğrusal denkleme koyduğumuzda etki yapması anlamındadır. Çoklu doğrusallık, ardışık bağımlılık sorunları kastedilmemektedir.
Regresyon analizinin tarihi
Regresyon yönteminin ilk şekli prensibidir ve ilk olarak Adrien Marie Legendre tarafından 1805 yılında ortaya atılmıştır. Hemen takiben 1809 yılında C.F. Gauss aynı yöntemi açıklamıştır. En küçük kareler terimi Legendre tarafından moindres carrés olarak kullanılmış, ancak Gauss aynı yöntemi 1795 yılından beri kullandığını iddia etmiştir. Legendre ve Gauss bu yöntemi astronomik gözlemlerden uydularının güneş etrafındaki yörüngelerini tespit etmek için kullanırken ortaya çıkartmışlardır. 1748 yılında Eüler'in aynı problem üzerinde uğraştığı, fakat başarı sağlayamadığı bilinmektedir. En küçük kareler kuramında sonraki gelişme Gauss'in 1821 yılında yayınladığı bir makalede ortaya çıkartılmış ve bu yayında Gauss sonradan kendi adı verilen teoreminin bir şeklini açıklamıştır.
Regresyon terimi 19. yüzyılda İngiliz istatistikçisi Francis Galton tarafından bir biyolojik inceleme için ortaya atılmıştır. Bu incelemenin ana konusu kalıtım olup, aile içinde baba ve annenin boyu ile çocukların boyu arasındaki bağlantıyı araştırmakta ve çocukların boylarının bir nesil içinde eski ata nesillerinin ortalamasına geri döndüklerini yani bir nesil içinde ortalamaya geri dönüş olduğu inceleme konusudur. Galton geri dönüş terimi için ilk yazısında İngilizce olarak reversion terimi kullanmışsa da sonradan aynı anlamda olan regression sözcüğü kullanmıştır. Bu çalışmalarında Galton istatistiksel 'regresyon' kavramını ve yöntemini de geliştirmiştir. ve bu yöntemi daha geniş genel istatistiksel alanlara uygulayıp geliştirmişlerdir... Bu yazılarda bağımlı ve bağımsız değişkenlerin normal dağılım gösterdiği varsayılmaktadır. Bu kısıtlayıcı varsayım 1922 ve 1925 yıllarındaki yayınları ile sadece bağımlı değişkenin koşullu dağılımının normal olduğu hallere uygulanmak üzere daha genişletilmiştir.).
Bu kavramları ve yöntemleri genel olarak, kalıtım konusu dışında "ortalamaya geri dönüş" ile hiçbir ilgisi olmayan konularda, kullanan istatistikçiler regresyon terimini kullanmakta devam etmişlerdir. Zamanımızda, bu terim, kavram ve yöntemin Galton'un konusu ile bütün ilişkisi yok olmuştur ve artık regresyon terimi doğrusal bağlantı bulunması ve eğri uydurma ile eş anlamlar vermektedir.
Temeldeki varsayımlar
Doğrusal regresyon yöntemini kullanmak için temelde şu varsayımların bulunduğu kabul edilmektedir:
- Çıkarımsal yöntem olduğu için kullanılan iki değişkenli örneklemin ya istatistiksel rastgele örneklem olduğu ya da anakütleyi çok iyi temsil ettiği bilinmektedir.
- Bağımlı değişken içinde hata bulunmaktadır. Bu hatanın bir rassal değişken olduğu ve ortalama hatanın sıfır olduğudur. da bulunması mümkündür ama bu hatanın incelemeye alınması regresyon analizi kapsamı dışındadır.
- Bağımsız değişken hatasızdır. Eğer bağımsız değişkende hata bulunduğu varsayılırsa özel bir yöntem şekli olan teknikler kullanılarak model kurulmalıdır.
- Hatalar zaman içinde ve kendi aralarında birbirine bağımlı değildir. Buna otokorelasyon veya bulunmaması varsayımı adı verilir.
- Hata varyansı sabittir ve veriler arasında hiç değişmediği varsayılır. Bu veya homoskedastisite varsayımı adı ile anılır. Eger bu varsayim uygun degilse yöntemi uygulanabilir.
- Hataların çapraz elamanları sabit hata varyansı olur ve matrisin diğer çapraz dışı elemanları 0 olur.
- Eğer çoklu regresyon analizi yapılıyor ve uc veya daha cok parametre icin kestirim isteniyorsa, bağımsız değişkenlerin birbirleri ile bağlantısının olmaması gereklidir. Buna (multicollinearity) olmaması varsayımı adı verilir.
- Hatalar bir normal dağılım gösterir. Eğer bu hataların normalliği varsayımı uygun değilse uygulanabilir.
Doğrusal regresyon
Anakütle doğrusal regresyon modeli
Doğrusal regresyonda, anakütle model belirlenmesine göre bağımlı değişken 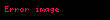



- dogru:
Burada 



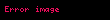
Çoklu doğrusal regresyonda iki veya daha çok sayıda bağımsız değişken veya bağımsız değişken fonksiyonu bulunur. Örneğin, önce verilmiş olan regresyon modeli yeni bir terim xi2 eklenerek degistirilirse; şu anakütle çoklu doğrusal regresyon modeli ortaya çıkar:
- parabol:
Denklemin sağ tarafındaki bağımsız değişken için bir ikinci derece (kuadratik) ifade bulunmasına rağmen bu model hala doğrusal regresyon modelidir; çünkü üç tane parametre, yani 


Daha genel çoklu doğrusal regresyon modelinde p tane bağımsız değişken olduğu varsayılır ve anakütle modeli şöyle ifade edilir:
veya biraz daha kısa olarak
İki Değişkenli regresyon katsayı kestirimleri
Anakütleden bir rastgele örneklem elde edilirse, bu 

Burada 
olur.
Bu örneklem regresyon denkleminin kestirimini elde etmenin yöntemi adi en küçük kareler (Ordinary least squares) olarak adlandırılır. Bu yönteme göre parametre kestirimleri kare toplamının minimum (en küçük) değerini bulmakla elde edilir. AKT şudur:
Bu fonksiyonun minimum değerini bulmak her parametre ile birinci kısımsal türevi alınarak sıfıra eşitlenir. Böylece her kısimsal türeve göre bir denklem elde edilir. Örneğin iki parametreli doğrusal regresyon için iki değişkenli iki denklem elde edilir. Bu simultane denklem sitemine adı verilir ve bu simultane denklemler sistemi birlikte çözülüp her anakütle parametresi için bir kestrim değeri bulunur.
İki parametreli basit doğrusal regresyon için iki anakütle parametre kestirimleri olan 
Burada bütün toplamlar i=1 den i=n kadardır ve örneklem toplamları, toplam kareleri ve toplam karşı çarpımı ile elde edilirler.
Bu iki değiskenli iki doğrusal denklem için çeşitli çözüm yolları vardır. Burada kullanılıp şu ifade elde edilir:
burada
Böylece iki parametreli doğrusal regresyon icin en küçük kareler parametre tahminleri için formüller şöyledir:
a
ve
Burada 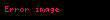




Çok değişkenli regresyon katsayı kestirimleri
Çok değişkenli regresyon için regresyon katsayısı kestrimi de iki değişkenli regresyon hâli gibi en küçük kareler yöntemi ile yapılır. Bu demektir ki kestirmde ortaya çıkacak artıkların karelerinin toplamı minimize edilecektir. Artıklar ri olur ve minimize edilecek objektif fonksiyon soyle ifade edilir:
Her bir artık, gözlemi yapılan bir değer ile kestirim modelini kullanarak elde edilen bir kestirim değeri arasındaki farktır:
En küçük kareler yöntemine göre S, toplam artıklar karesi, minimize edilecektir. Belirli koşullar gecerli ise, elde edilecek parametre kestrimleri ( göre) en küçük varyans gösteren kestirim ve hatta özelliği gösteren dogrusal kestirim olabilirler.
Anakütle regresyon katsayılarının kestirim regresyon katsayıları için bir ^ (şapka) notasyonu kullanılanılır: yani 
Matris notasyonu kullanılırsa, normal denklemler şöyle yazılabilir:
Eğer 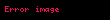
,
Bu tahminleridir.
Hatalar varyansı ve toplam kareler
Anakütle hatalarının normal dağılım gösterdiğine dair bir diğer varsayımı da kullanarak incelemeci önce hatalar varyansı ve toplam kareler değerlerini bulur ve bunları kullanarak tahmin edilen denklem ve parametreler üzerinde çıkarımsal istatistik sonuçlara varabilir.
Anakütle hata teriminin sabit bir varyansı bulunduğu varsayımına göre, hatalar varyansı kestirimi şöyle bulunur:
Bu ifadeye regresyon için adı verilir. Parametre kestirimleri için standart hata şöyle bulunur:
Örneklem veri serisinin değişebilirliği değişik suretiyle ifade edilebilirler.
- Tüm toplam kareler (örneklem varyansına orantılı olur):
.
- Regresyon toplam kareler: Bazen açıklanan toplam kareler diye anılır.
- Toplam hatalar karesi: Artıklar toplam karesi olarak da isimlendirilir.
Bir regresyon modeli için parametreler, en küçük kareler yöntemi kullanılarak, tahmin edildikten sonra regresyon kontrol etme yöntemleri (yani çıkarımsal kontrol) uygulamak gerekir. Bunlar bulunan tahmin edilmiş genel doğrusal denklemin örnekleme sınaması ve kestirimci regresyon katsayılarının tektek istatistiksel anlamlılığını sınamak veya güvenlik aralığı sağlamak olarak özetlenir.
Kestirim denklemin genel uyum iyiliğinin çıkarımsal kontrolü
Tahmin edilen doğrusal regresyon denkleminin genel olarak örnekleme uygun olup olmadığı için uygulanan çıkarımsal istatistik işlemleri iki türde olabilir:
- yani değerinin bulunması;
- regresyon denklemine F-sınaması uygulaması.
Bu iki çıkarımsal kontrol aynı konunun çıkarımsal kontrolü için kullanılır: tahmin regresyon denkleminin tümünün uygun olup olmadığı. Bu nedenle iki yöntemden tek birini kullanmak yeterlidir. Buna rağmen birçok pratik analizde her iki çıkarımsal analiz de kullanılmaktadır; çünkü ikisinde hesaplanması için nerede ise aynı yöntem kullanılır ve eger istatistik veya ekonometrik kompüter paketi kullanılırsa her iki yöntem için gerekli sonuçlar birlikte verilir.
Belirleme katsayısı yani R-kare (R2) değeri
yani (R2) ) R-kare) için en genel tanımlama förmülü sudur:
yani (1-toplam hatalar karesi) ile (tüm toplam kareler) oranı; veya (1-Artıklar toplam karesi) ile (tüm toplam kareler) oranı.
Çıkarımsal analizde R-kare değeri bulunur ve bulunan değer doğru hesaplanmışsa 0 ile 1 arasında olmalıdır. Yapılan bu analiz ceşitli hallerde açıklanabilir:
- Eğer sadece iki değiskenli (Y ve X0) regresyon analizi yapılıyorsa, geometrik olarak X-Y düzeyinde doğrusal regresyon tahmini bu düzeyde olan noktalara en-küçük-kareler prensibine göre en iyi uyan bir doğru uydurmaktır. Eğer bütün noktalar bu tahmin edilen doğru üzerinde ise tahmin edilen doğru uyumu bu veri noktaları için hiç hatasızdır ve veri noktaları doğrudan hiç ayrılık göstermez. Hat varyasyonu bu halde sıfır olur. Bu veri noktaları tahmin edilen doğrudan uzaklaştıkça hatalar varyasyonu çoğalmaktadır.
- Üç değişkenli (Y ve X1 ve X2 değişkenli) çoklu regresyonda ise tahmin edilen bir üç boyutlu düzeydir. Eger bu düzey veri noktalarına tam olarak uyarsa bütün veri noktaları tahmin edilen düzey üstüne düşerler. Veri noktaları tahmin edilen düzey etrafında dağılmaya başlarlarsa, hatalar varyasyonu artmaya başlar.
- Üç değişkenden daha çoklu değişkenli regresyon analizi ise grafik olarak verilemez; çok boyutlu uzayı gösterir ve tahmin edilen regresyon katsayıları ise bu cok boyutlu uzayda bir hiper-düzey ortaya çıkartır ve bu hiper-düzeyden ayrılmalar hata varyasyonudur.
Genel olarak:
- Eğer R2 değeri sıfıra yakınsa, uygun olmadığı kabul edilir. Bu sonuç ortaya çıkarsa toplanan verilere kullanılan modelin uygun olmadığı sonucu çıkarılır ve bu uygunsuzluk modelinin değiştirilmesini gerektirir. Bu demektir ki model ile açıklanan varyasyon tüm varyansyonu %0ini açıklamakta ve geometrik olarak orneklem verileri regresyon ile elde edilen hiperduzeyin etrafına çok dağılmış olarak bulunmaktadırlar. Bu çıkarıma varılırsa bu basamağa kadar yapılmış olan analizin bir kenara bırakılması ve diğer bir modelin bulunup kullanılması gerekir.
- Eğer R2 değeri bire yakınsa, uygun olduğu sonucu çıkarılır. Geometrik olarak çok değişken boyutlu uzayda, örneklem veri noktalarının hepsi uzayda dağılma göstermeyip hemen hepsi regresyon ile elde edilen hiperduzey üzerinde bulunmaktadır. Bu halde çıkarımsal kontrol analizinin diğer basamağına geçilir.
F-testi
Regresyon denklem uyum iyiliği için F-testi için sıfır hipotez (H0) anakutle model katsayilarinin hepsinin değerinin 0 (sifir)a eşit olduğudur. Yani sıfır hipotez gerçekse hesap ile elde edilen katsayi kestirimlerinin hepsi anakütle için 0dir yani hiçbir etki ve bağlantı anlamı vermez. Bu basamağa kadar yapılmış olan analizin bir kenara bırakılması ve diğer bir modelin bulunup kullanılması gerekir. Eğer sıfır hipotez reddedilirse regresyon kestirimleri genellikle uygundur ve cikarimsal kontrol analizine devam edilir.
Kestirimi yapılan her tek regresyon parametresinin değerinin çıkarımsal kontrolü
Yani bu tahmin edilmiş standart hataları kullanarak her tek anakütle regresyon parametresi hakkında kestirim güvenlik aralıkları kurabilir ve hipotez sınamaları yapılabilir.
İnterpolasyon ve ekstrapolasyon
Regresyon modelleri kullanarak kestirim yapılmak istenirse, bağımsız değişken olan 


Eğer bu kestirim, modeli kurmak için kullanılan 
Diğer yaklaşımlar
Ağırlıklı en küçük kareler yöntemi
yöntemi kullanılırken yapılan temel varsayımlarindan biri hata terimi varyanslarının birbirine esit olduğudur. Eğer gözlem hataları birbirine eşit olmayan hata terimi varyanslari gösteriyorlarsa, en küçük kareler yönteminin bu önemli varsayımı ihlal edilmiş olur ve en küçük kareler yöntemi ile elde edilen regresyon kestirimleri anlamlı olmayabilir. Bu sorunu çözümlemek için her gözleme ayrı ağırlık vererek en küçük kareler yöntemi uygulamak imkânı vardır ve bu genelleştirmeye adı verilir. ,değişkenlere ağırlık vererek veya değişkenlerin önem derecesini değiştirerek uygulanan en küçük kareler yöntemidir.
Değişkenlerde-hatalar modeli
yöntemi kullanılırken yapılan temel varsayımlarından biri de gözlem hatalarının yalnızca bağımlı değişkenlerde yapıldığı ve bağımsız değişkende gözlem hatası bulunmadığıdır. Eğer bağımlı değişkende hata bulunduğu ve bunun elde edilen regresyon kestirim değerlerine çok etki yaptığı bilinirse, veya diğer ismi ile modeli ve bu modelle ilişkili kestirim yöntemleri kullanılabilir.
Genelleştirilmiş doğrusal model
Eğer anakütle regresyon modeli içindeki hatalar için olasılık dağılım fonksiyonu bir normal dağılım göstermiyorsa kullanılabilir. Bu halde hatalarin olasılık dağılım fonksiyonu , gamma dağılımı, , Poisson dağılımı, binom dağılım, vb. olabilir.
Güçlü regresyon
Ayrık bağımlı değişken
Doğrusal olmayan regresyon
Eğer değişkenler hakkında kurulan teori dolayasıyla anakutle modeli parametrelri ile doğrusal değilse, kestirim yapılırken toplam kareleri tekrarlama usulu kullanarak minimize edilmesi gerekir. Bu kullanılan tekrarlama yöntemi birçok karışık sorunlar ortaya çıkarır. Bunların özet olarak incelenmesi için (doğrusal olmayan regresyon#Dogrusal olmayan ve dogrusal en kucuk kareler arasindaki farklar) maddesine bakiniz.
İçsel kaynaklar
Kaynakça
- ^ a b c d e f g h i j k Gujarati, Damodar (çev. Ümit Şenesen, Gülay Günlük Şenesen) (2008) Temel Ekonometri, Literatür Yayınları .
- ^ A.M. Legendre (1805), Nouvelles méthodeş pour la détermination des orbites des comètes. “Sur la Méthode des moindres quarrés” bir ek bölümde bulunur.
- ^ C.F. Gauss (1809), Theoria Motus Corporum Coeleştium in Sectionibüs Conicis Şölem Ambientum.
- ^ C.F. Gauss (1821/1823). Theoria çombinationis observationum erroribüs minimiş obnoxiae.
- ^ Francis Galton (1877), "Typical laws of heredity", Nature 15, 492-495, 512-514, 532-533. (Galton burada bezelyelerle yaptığı kalıtım deneyi sonucunda reversion terimi kullanır.)
- ^ Francis Galton (1885) Presidential address, Section H, Anthropology.(Burada insanlarin boylari uzerinde yaptigi arastirma sonucu için "regression" terimi kullanir.)
- ^ G. Udny Yule (1897) "On the Theory of Correlation", J. Royal Statist. Soç., 1897, p. 812-54.
- ^ Karl Pearson, G.U.Yüle, Norman Blanchard, and Alice Lee (1903). "The Law of Ancestral Heredity",
- ^ R.A. Fisher (1922), "The goodness of fit of regression formulae, and the distribution of regression çoefficients", J. Royal Statist. Soç., 85, 597-612
- ^ R.A. Fisher (1925),
Bibliyografya
- Gujarati, Damodar (çev. Ümit Şenesen, Gülay Günlük Şenesen) (2008) Temel Ekonometri, Literatür Yayınları .
- Audi, R., Ed. (1996). "Curve fitting problem," The Cambridge Dictionary of Philosophy. Cambridge, Cambridge University Press. pp. 172–173. (İngilizce)
- and Judith M. Tanur, ed. (1978), "Linear Hypotheses," International Encyclopedia of Statistics. Free Press, cilt 1 (İngilizce)
- Evan J. Williams, "I. Regression," say. 523-41.
- , "II. Analysis of Variance," pp. 541-554.
- (1987). "Regression and correlation analysis," , Cilt. 4, say. 120-23. (İngilizce)
- Birkes, David and Yadolah Dodge, Alternative Methods of Regression. (İngilizce)
- Chatfield, C. (1993) "Calculating Interval Forecasts," Journal of Business and Economic Statistics, 11. pp. 121–135. (İngilizce)
- Dinçer, F. "Regresyon Kelimesinin Tarihi",[1]20 Mayıs 2008 tarihinde Wayback Machine sitesinde .
- Draper, N.R. ve Smith, H. (1998).Applied Regression Analysis Wiley Series in Probability and Statistics (İngilizce)
- Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage (İngilizce)
- Hardle, W., Applied Nonparametric Regression (1990), (İngilizce)
- Meade, N. ve T. Islam (1995) "Prediction Intervals for Growth Curve Forecasts," Journal of Forecasting, 14, say. 413-430. (İngilizce)
- Munro, Barbara Hazard (2005) "Statistical Methods for Health Care Research 5th ed." Lippincott Williams & Wilkins, (İngilizce)
- Sykes, A.O. (Innaugural Coase Lecture)
- Kotsiantis,S., Kanellopoulos,D. ve Pintelas,P. (2006) "Local Additive Regression of Decision Stumps", Lecture Notes in Artificial Intelligence, Springer-Verlag, Vol. 3955, SETN 2006, say.. 148 – 157 (İngilizce)
- Kotsiantis,S. ve Pintelas, P. (2005) "Selective Averaging of Regression Models", Annals of Mathematics, Computing & TeleInformatics, Cilt 1, No 3, say. 66-75 (İngilizce)
Dış bağlantılar
| Wikimedia Commons'ta Regresyon analizi ile ilgili ortam dosyaları bulunmaktadır. |
- Regresyon analizi12 Nisan 2009 tarihinde Wayback Machine sitesinde .
- Curvefit: A complete guide to nonlinear regression21 Temmuz 2009 tarihinde Wayback Machine sitesinde . - Online ders kitabı
- Doğrusal model üzerine yorumlar2 Temmuz 2010 tarihinde Wayback Machine sitesinde . - Bill Venbables tarafından bazı doğrusal regresyon modelleri üzerinde birkaç yorum.
- - Doğrusal regresyon için örnek. Doğrusal regresyon denkleminin, varyansların, standart hataların, korelasyon katsayısının, belirleme katsayısının ve güvenlik aralıklarının nasıl bulunduğunu göstermektedir.
- Zayif korelasyon bağlantılı verilerin regresyonu14 Mart 2010 tarihinde Wayback Machine sitesinde . - Y -aralığı X-aralığından çok daha küçük olursa nasıl regresyon hataları ortaya çıkabilir.
- xuru.org11 Nisan 2010 tarihinde Wayback Machine sitesinde . Online regresyon avadanlığı
- - Aktif öğrenme + Model seçimi + Vekil modeli regresyonu için Matlab yazılımı
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Regresyon analizi iki ya da daha cok nicel degisken arasindaki iliskiyi olcmek icin kullanilan analiz metodudur Eger tek bir degisken kullanilarak analiz yapiliyorsa buna tek degiskenli regresyon birden cok degisken kullaniliyorsa cok degiskenli regresyon analizi olarak isimlendirilir Regresyon analizi ile degiskenler arasindaki iliskinin varligi eger iliski var ise bunun gucu hakkinda bilgi edinilebilir Regresyon terimi icin oz Turkce olarak baglanim sozcugu kullanilmasi teklif edilmis ise de Turk ekonometriciler arasinda bu kullanim yaygin degildir Ornegin bir ziraat muhendisi bugday verimi ve gubre miktari arasindaki iliskiyi bir muhendis basinc ve sicaklik bir ekonomist gelir duzeyi ve tuketim harcamalari bir egitimci ogrencilerin devamsizlik gosterdigi gun sayilari ve basari dereceleri arasindaki iliskiyi bilmek isteyebilir Regresyon iki ya da daha cok degisken arasindaki dogrusal iliskinin fonksiyonel seklini biri bagimli digeri bagimsiz degisken olarak bir dogru denklemi olarak gostermekle kalmaz degiskenlerden birinin degeri bilindiginde digeri hakkinda kestirim yapilmasini saglar Genellikle bu iki veya cok degiskenlerin hepsinin niceliksel olcekli olmasi zorunlulugu vardir Regresyonda degiskenlerden biri bagimli digerleri bagimsiz degisken olmalidir Buradaki mantik esitligin solunda yer alan degiskenin saginda yer alan degiskenlerden etkilenmesidir Sagda yer alan degiskenlerse diger degiskenlerden etkilenmemektedir Burada etkilenmemek matematiksel anlamda bu degiskenleri bir dogrusal denkleme koydugumuzda etki yapmasi anlamindadir Coklu dogrusallik ardisik bagimlilik sorunlari kastedilmemektedir Regresyon analizinin tarihiRegresyon yonteminin ilk sekli prensibidir ve ilk olarak Adrien Marie Legendre tarafindan 1805 yilinda ortaya atilmistir Hemen takiben 1809 yilinda C F Gauss ayni yontemi aciklamistir En kucuk kareler terimi Legendre tarafindan moindres carres olarak kullanilmis ancak Gauss ayni yontemi 1795 yilindan beri kullandigini iddia etmistir Legendre ve Gauss bu yontemi astronomik gozlemlerden uydularinin gunes etrafindaki yorungelerini tespit etmek icin kullanirken ortaya cikartmislardir 1748 yilinda Euler in ayni problem uzerinde ugrastigi fakat basari saglayamadigi bilinmektedir En kucuk kareler kuraminda sonraki gelisme Gauss in 1821 yilinda yayinladigi bir makalede ortaya cikartilmis ve bu yayinda Gauss sonradan kendi adi verilen teoreminin bir seklini aciklamistir Regresyon terimi 19 yuzyilda Ingiliz istatistikcisi Francis Galton tarafindan bir biyolojik inceleme icin ortaya atilmistir Bu incelemenin ana konusu kalitim olup aile icinde baba ve annenin boyu ile cocuklarin boyu arasindaki baglantiyi arastirmakta ve cocuklarin boylarinin bir nesil icinde eski ata nesillerinin ortalamasina geri donduklerini yani bir nesil icinde ortalamaya geri donus oldugu inceleme konusudur Galton geri donus terimi icin ilk yazisinda Ingilizce olarak reversion terimi kullanmissa da sonradan ayni anlamda olan regression sozcugu kullanmistir Bu calismalarinda Galton istatistiksel regresyon kavramini ve yontemini de gelistirmistir ve bu yontemi daha genis genel istatistiksel alanlara uygulayip gelistirmislerdir Bu yazilarda bagimli ve bagimsiz degiskenlerin normal dagilim gosterdigi varsayilmaktadir Bu kisitlayici varsayim 1922 ve 1925 yillarindaki yayinlari ile sadece bagimli degiskenin kosullu dagiliminin normal oldugu hallere uygulanmak uzere daha genisletilmistir Bu kavramlari ve yontemleri genel olarak kalitim konusu disinda ortalamaya geri donus ile hicbir ilgisi olmayan konularda kullanan istatistikciler regresyon terimini kullanmakta devam etmislerdir Zamanimizda bu terim kavram ve yontemin Galton un konusu ile butun iliskisi yok olmustur ve artik regresyon terimi dogrusal baglanti bulunmasi ve egri uydurma ile es anlamlar vermektedir Temeldeki varsayimlarDogrusal regresyon yontemini kullanmak icin temelde su varsayimlarin bulundugu kabul edilmektedir Cikarimsal yontem oldugu icin kullanilan iki degiskenli orneklemin ya istatistiksel rastgele orneklem oldugu ya da anakutleyi cok iyi temsil ettigi bilinmektedir Bagimli degisken icinde hata bulunmaktadir Bu hatanin bir rassal degisken oldugu ve ortalama hatanin sifir oldugudur da bulunmasi mumkundur ama bu hatanin incelemeye alinmasi regresyon analizi kapsami disindadir Bagimsiz degisken hatasizdir Eger bagimsiz degiskende hata bulundugu varsayilirsa ozel bir yontem sekli olan teknikler kullanilarak model kurulmalidir Hatalar zaman icinde ve kendi aralarinda birbirine bagimli degildir Buna otokorelasyon veya bulunmamasi varsayimi adi verilir Hata varyansi sabittir ve veriler arasinda hic degismedigi varsayilir Bu veya homoskedastisite varsayimi adi ile anilir Eger bu varsayim uygun degilse yontemi uygulanabilir Hatalarin capraz elamanlari sabit hata varyansi olur ve matrisin diger capraz disi elemanlari 0 olur Eger coklu regresyon analizi yapiliyor ve uc veya daha cok parametre icin kestirim isteniyorsa bagimsiz degiskenlerin birbirleri ile baglantisinin olmamasi gereklidir Buna multicollinearity olmamasi varsayimi adi verilir Hatalar bir normal dagilim gosterir Eger bu hatalarin normalligi varsayimi uygun degilse uygulanabilir Dogrusal regresyonAnakutle dogrusal regresyon modeli Dogrusal regresyonda anakutle model belirlenmesine gore bagimli degisken yi displaystyle y i parametrelerin bir olur Dikkat edilirse parametrelerden bahis edilmektedir cunku bagimsiz degiskenlerin bir dogrusal bilesigi olmasi gerekli degildir Ornegin tek bir bagimsiz degiskenli xi displaystyle x i ve iki parametreli b0 displaystyle beta 0 ve b1 displaystyle beta 1 dogru yi b0 b1xi ϵi i 1 n displaystyle y i beta 0 beta 1 x i epsilon i i 1 n Burada ϵi displaystyle epsilon i bir hata terimidir ve i displaystyle i alt indeksleri bir belirlenmis mumkun gozlemi ifade eder Ayrica ϵi displaystyle epsilon i i displaystyle i nci gozlemin regresyon dogrusuna olan uzakligini ifade etmekte olup ortalamasi 0 ve varyansi s2 displaystyle sigma 2 olan bir normal dagilis gosterir Coklu dogrusal regresyonda iki veya daha cok sayida bagimsiz degisken veya bagimsiz degisken fonksiyonu bulunur Ornegin once verilmis olan regresyon modeli yeni bir terim xi2 eklenerek degistirilirse su anakutle coklu dogrusal regresyon modeli ortaya cikar parabol yi b0 b1xi b2xi2 ϵi i 1 m displaystyle y i beta 0 beta 1 x i beta 2 x i 2 epsilon i i 1 m Denklemin sag tarafindaki bagimsiz degisken icin bir ikinci derece kuadratik ifade bulunmasina ragmen bu model hala dogrusal regresyon modelidir cunku uc tane parametre yani b0 displaystyle beta 0 b1 displaystyle beta 1 ve b2 displaystyle beta 2 ile coklu degiskenli dogrusaldir Daha genel coklu dogrusal regresyon modelinde p tane bagimsiz degisken oldugu varsayilir ve anakutle modeli soyle ifade edilir yi b0 b1x1i bpxpi ei displaystyle y i beta 0 beta 1 x 1i cdots beta p x pi varepsilon i veya biraz daha kisa olarak yi b0 j 1pXijbj ei displaystyle y i beta 0 sum j 1 p X ij beta j varepsilon i Iki Degiskenli regresyon katsayi kestirimleri Anakutleden bir rastgele orneklem elde edilirse bu bi displaystyle beta i anakutle parametreleri icin orneklem tahminleri b i displaystyle widehat beta i bulunur ve su orneklem dogrusal regresyon denklemi elde edilir yi b 0 b 1Xi ei displaystyle y i widehat beta 0 widehat beta 1 X i e i Burada ei displaystyle e i terimi orneklemden elde edilen artik olur ve ei yi y i displaystyle e i y i widehat y i olur Bu orneklem regresyon denkleminin kestirimini elde etmenin yontemi adi en kucuk kareler Ordinary least squares olarak adlandirilir Bu yonteme gore parametre kestirimleri kare toplaminin minimum en kucuk degerini bulmakla elde edilir AKT sudur AKT i 1Nei2 displaystyle AKT sum i 1 N e i 2 Bu fonksiyonun minimum degerini bulmak her parametre ile birinci kisimsal turevi alinarak sifira esitlenir Boylece her kisimsal tureve gore bir denklem elde edilir Ornegin iki parametreli dogrusal regresyon icin iki degiskenli iki denklem elde edilir Bu simultane denklem sitemine adi verilir ve bu simultane denklemler sistemi birlikte cozulup her anakutle parametresi icin bir kestrim degeri bulunur Iki parametreli basit dogrusal regresyon icin iki anakutle parametre kestirimleri olan b 0 b 1 displaystyle widehat beta 0 widehat beta 1 su normal denklemlerin birlikte cozulmesi ile elde edilir m a xi b yi xi a xi2 b xiyi displaystyle begin array lcl m alpha sum x i beta sum y i sum x i alpha sum x i 2 beta sum x i y i end array Burada butun toplamlar i 1 den i n kadardir ve orneklem toplamlari toplam kareleri ve toplam karsi carpimi ile elde edilirler Bu iki degiskenli iki dogrusal denklem icin cesitli cozum yollari vardir Burada kullanilip su ifade elde edilir b m xiyi xi yiD xi x yi y xi x 2 displaystyle hat beta frac m sum x i y i sum x i sum y i Delta frac sum x i bar x y i bar y sum x i bar x 2 a xi2 yi xi xiyiD y x b displaystyle hat alpha frac sum x i 2 sum y i sum x i sum x i y i Delta bar y bar x hat beta burada D m xi2 xi 2 displaystyle Delta m sum x i 2 left sum x i right 2 Boylece iki parametreli dogrusal regresyon icin en kucuk kareler parametre tahminleri icin formuller soyledir b1 xi x yi y xi x 2 displaystyle widehat beta 1 frac sum x i bar x y i bar y sum x i bar x 2 a ve b0 y b1 x displaystyle hat beta 0 bar y widehat beta 1 bar x Burada x displaystyle bar x x displaystyle x gozlem degerlerinin ortalamasi ve y displaystyle bar y ise y displaystyle y gozlem degerlerinin ortalamasidir Bir veri serisi icin kirmizi noktalar dogrusal regresyon Cok degiskenli regresyon katsayi kestirimleri Cok degiskenli regresyon icin regresyon katsayisi kestrimi de iki degiskenli regresyon hali gibi en kucuk kareler yontemi ile yapilir Bu demektir ki kestirmde ortaya cikacak artiklarin karelerinin toplami minimize edilecektir Artiklar ri olur ve minimize edilecek objektif fonksiyon soyle ifade edilir S i 1mri2 displaystyle S sum i 1 m r i 2 Her bir artik gozlemi yapilan bir deger ile kestirim modelini kullanarak elde edilen bir kestirim degeri arasindaki farktir ri yi j 1nXijb j displaystyle r i y i sum j 1 n X ij hat beta j En kucuk kareler yontemine gore S toplam artiklar karesi minimize edilecektir Belirli kosullar gecerli ise elde edilecek parametre kestrimleri gore en kucuk varyans gosteren kestirim ve hatta ozelligi gosteren dogrusal kestirim olabilirler Anakutle regresyon katsayilarinin kestirim regresyon katsayilari icin bir sapka notasyonu kullanilanilir yani b i displaystyle hat beta i Genellikle cok degiskenli regresyon icin soyle ifade edilir i 1N p 1pXijXikb k i 1NXijyi j 1 p displaystyle sum i 1 N sum p 1 p X ij X ik hat beta k sum i 1 N X ij y i j 1 p Matris notasyonu kullanilirsa normal denklemler soyle yazilabilir XTX b XTy displaystyle mathbf left X T X right hat boldsymbol beta X T y Eger XTX displaystyle X T X matrisi singuler degilse b XTX 1XTy displaystyle boldsymbol hat beta mathbf left X T X right 1 X T y Bu tahminleridir Hatalar varyansi ve toplam kareler Anakutle hatalarinin normal dagilim gosterdigine dair bir diger varsayimi da kullanarak incelemeci once hatalar varyansi ve toplam kareler degerlerini bulur ve bunlari kullanarak tahmin edilen denklem ve parametreler uzerinde cikarimsal istatistik sonuclara varabilir Anakutle hata teriminin sabit bir varyansi bulundugu varsayimina gore hatalar varyansi kestirimi soyle bulunur se SSEN 2 displaystyle hat sigma varepsilon sqrt frac SSE N 2 Bu ifadeye regresyon icin adi verilir Parametre kestirimleri icin standart hata soyle bulunur s b0 s e1N x 2 xi x 2 displaystyle hat sigma beta 0 hat sigma varepsilon sqrt frac 1 N frac bar x 2 sum x i bar x 2 s b1 s e1 xi x 2 displaystyle hat sigma beta 1 hat sigma varepsilon sqrt frac 1 sum x i bar x 2 Orneklem veri serisinin degisebilirligi degisik suretiyle ifade edilebilirler Tum toplam kareler orneklem varyansina orantili olur SStot i yi y 2 displaystyle SS rm tot sum i y i bar y 2 Regresyon toplam kareler Bazen aciklanan toplam kareler diye anilir SSreg i fi f 2 displaystyle SS rm reg sum i f i bar f 2 Toplam hatalar karesi Artiklar toplam karesi olarak da isimlendirilir SSerr i yi fi 2 displaystyle SS rm err sum i y i f i 2 Bir regresyon modeli icin parametreler en kucuk kareler yontemi kullanilarak tahmin edildikten sonra regresyon kontrol etme yontemleri yani cikarimsal kontrol uygulamak gerekir Bunlar bulunan tahmin edilmis genel dogrusal denklemin ornekleme sinamasi ve kestirimci regresyon katsayilarinin tektek istatistiksel anlamliligini sinamak veya guvenlik araligi saglamak olarak ozetlenir Kestirim denklemin genel uyum iyiliginin cikarimsal kontrolu Tahmin edilen dogrusal regresyon denkleminin genel olarak ornekleme uygun olup olmadigi icin uygulanan cikarimsal istatistik islemleri iki turde olabilir yani degerinin bulunmasi regresyon denklemine F sinamasi uygulamasi Bu iki cikarimsal kontrol ayni konunun cikarimsal kontrolu icin kullanilir tahmin regresyon denkleminin tumunun uygun olup olmadigi Bu nedenle iki yontemden tek birini kullanmak yeterlidir Buna ragmen bircok pratik analizde her iki cikarimsal analiz de kullanilmaktadir cunku ikisinde hesaplanmasi icin nerede ise ayni yontem kullanilir ve eger istatistik veya ekonometrik komputer paketi kullanilirsa her iki yontem icin gerekli sonuclar birlikte verilir Belirleme katsayisi yani R kare R2 degeri yani R2 R kare icin en genel tanimlama formulu sudur R2 1 SSerrSStot displaystyle R 2 equiv 1 SS rm err over SS rm tot yani 1 toplam hatalar karesi ile tum toplam kareler orani veya 1 Artiklar toplam karesi ile tum toplam kareler orani Cikarimsal analizde R kare degeri bulunur ve bulunan deger dogru hesaplanmissa 0 ile 1 arasinda olmalidir Yapilan bu analiz cesitli hallerde aciklanabilir Eger sadece iki degiskenli Y ve X0 regresyon analizi yapiliyorsa geometrik olarak X Y duzeyinde dogrusal regresyon tahmini bu duzeyde olan noktalara en kucuk kareler prensibine gore en iyi uyan bir dogru uydurmaktir Eger butun noktalar bu tahmin edilen dogru uzerinde ise tahmin edilen dogru uyumu bu veri noktalari icin hic hatasizdir ve veri noktalari dogrudan hic ayrilik gostermez Hat varyasyonu bu halde sifir olur Bu veri noktalari tahmin edilen dogrudan uzaklastikca hatalar varyasyonu cogalmaktadir Uc degiskenli Y ve X1 ve X2 degiskenli coklu regresyonda ise tahmin edilen bir uc boyutlu duzeydir Eger bu duzey veri noktalarina tam olarak uyarsa butun veri noktalari tahmin edilen duzey ustune duserler Veri noktalari tahmin edilen duzey etrafinda dagilmaya baslarlarsa hatalar varyasyonu artmaya baslar Uc degiskenden daha coklu degiskenli regresyon analizi ise grafik olarak verilemez cok boyutlu uzayi gosterir ve tahmin edilen regresyon katsayilari ise bu cok boyutlu uzayda bir hiper duzey ortaya cikartir ve bu hiper duzeyden ayrilmalar hata varyasyonudur Genel olarak Eger R2 degeri sifira yakinsa uygun olmadigi kabul edilir Bu sonuc ortaya cikarsa toplanan verilere kullanilan modelin uygun olmadigi sonucu cikarilir ve bu uygunsuzluk modelinin degistirilmesini gerektirir Bu demektir ki model ile aciklanan varyasyon tum varyansyonu 0ini aciklamakta ve geometrik olarak orneklem verileri regresyon ile elde edilen hiperduzeyin etrafina cok dagilmis olarak bulunmaktadirlar Bu cikarima varilirsa bu basamaga kadar yapilmis olan analizin bir kenara birakilmasi ve diger bir modelin bulunup kullanilmasi gerekir Eger R2 degeri bire yakinsa uygun oldugu sonucu cikarilir Geometrik olarak cok degisken boyutlu uzayda orneklem veri noktalarinin hepsi uzayda dagilma gostermeyip hemen hepsi regresyon ile elde edilen hiperduzey uzerinde bulunmaktadir Bu halde cikarimsal kontrol analizinin diger basamagina gecilir F testi Regresyon denklem uyum iyiligi icin F testi icin sifir hipotez H0 anakutle model katsayilarinin hepsinin degerinin 0 sifir a esit oldugudur Yani sifir hipotez gercekse hesap ile elde edilen katsayi kestirimlerinin hepsi anakutle icin 0dir yani hicbir etki ve baglanti anlami vermez Bu basamaga kadar yapilmis olan analizin bir kenara birakilmasi ve diger bir modelin bulunup kullanilmasi gerekir Eger sifir hipotez reddedilirse regresyon kestirimleri genellikle uygundur ve cikarimsal kontrol analizine devam edilir Kestirimi yapilan her tek regresyon parametresinin degerinin cikarimsal kontrolu Yani bu tahmin edilmis standart hatalari kullanarak her tek anakutle regresyon parametresi hakkinda kestirim guvenlik araliklari kurabilir ve hipotez sinamalari yapilabilir Interpolasyon ve ekstrapolasyon Regresyon modelleri kullanarak kestirim yapilmak istenirse bagimsiz degisken olan x displaystyle x degisken veri degerleri verilirse bagimli degisken y displaystyle y icin kestrim degerleri fi displaystyle f i tahmin etmek icin kullanabilirler Eger bu kestirim modeli kurmak icin kullanilan x displaystyle x degisken degerleri icin yapiliyorsa bu islem interpolasyon olarak adlandirilir Eger kestirim modeli kurmak icin kullanilan bagimsiz degisken degerlerinin disindaki degerler ile yapilirsa ekstrapolasyon olarak adlandirilir ve ekstrapolasyon cok daha yanli olabilir Diger yaklasimlarAgirlikli en kucuk kareler yontemi yontemi kullanilirken yapilan temel varsayimlarindan biri hata terimi varyanslarinin birbirine esit oldugudur Eger gozlem hatalari birbirine esit olmayan hata terimi varyanslari gosteriyorlarsa en kucuk kareler yonteminin bu onemli varsayimi ihlal edilmis olur ve en kucuk kareler yontemi ile elde edilen regresyon kestirimleri anlamli olmayabilir Bu sorunu cozumlemek icin her gozleme ayri agirlik vererek en kucuk kareler yontemi uygulamak imkani vardir ve bu genellestirmeye adi verilir degiskenlere agirlik vererek veya degiskenlerin onem derecesini degistirerek uygulanan en kucuk kareler yontemidir Degiskenlerde hatalar modeli yontemi kullanilirken yapilan temel varsayimlarindan biri de gozlem hatalarinin yalnizca bagimli degiskenlerde yapildigi ve bagimsiz degiskende gozlem hatasi bulunmadigidir Eger bagimli degiskende hata bulundugu ve bunun elde edilen regresyon kestirim degerlerine cok etki yaptigi bilinirse veya diger ismi ile modeli ve bu modelle iliskili kestirim yontemleri kullanilabilir Genellestirilmis dogrusal model Eger anakutle regresyon modeli icindeki hatalar icin olasilik dagilim fonksiyonu bir normal dagilim gostermiyorsa kullanilabilir Bu halde hatalarin olasilik dagilim fonksiyonu gamma dagilimi Poisson dagilimi binom dagilim vb olabilir Guclu regresyon Ayrik bagimli degisken Dogrusal olmayan regresyon Eger degiskenler hakkinda kurulan teori dolayasiyla anakutle modeli parametrelri ile dogrusal degilse kestirim yapilirken toplam kareleri tekrarlama usulu kullanarak minimize edilmesi gerekir Bu kullanilan tekrarlama yontemi bircok karisik sorunlar ortaya cikarir Bunlarin ozet olarak incelenmesi icin dogrusal olmayan regresyon Dogrusal olmayan ve dogrusal en kucuk kareler arasindaki farklar maddesine bakiniz Icsel kaynaklarEkstrapolasyon Tahmin araligi Istatistik Cokdegisirli normal dagilimKaynakca a b c d e f g h i j k Gujarati Damodar cev Umit Senesen Gulay Gunluk Senesen 2008 Temel Ekonometri Literatur Yayinlari ISBN 975 7860 99 9 A M Legendre 1805 Nouvelles methodes pour la determination des orbites des cometes Sur la Methode des moindres quarres bir ek bolumde bulunur C F Gauss 1809 Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum C F Gauss 1821 1823 Theoria combinationis observationum erroribus minimis obnoxiae Francis Galton 1877 Typical laws of heredity Nature 15 492 495 512 514 532 533 Galton burada bezelyelerle yaptigi kalitim deneyi sonucundareversionterimi kullanir Francis Galton 1885 Presidential address Section H Anthropology Burada insanlarin boylari uzerinde yaptigi arastirma sonucu icin regression terimi kullanir G Udny Yule 1897 On the Theory of Correlation J Royal Statist Soc 1897 p 812 54 Karl Pearson G U Yule Norman Blanchard and Alice Lee 1903 The Law of Ancestral Heredity R A Fisher 1922 The goodness of fit of regression formulae and the distribution of regression coefficients J Royal Statist Soc 85 597 612 R A Fisher 1925 BibliyografyaGujarati Damodar cev Umit Senesen Gulay Gunluk Senesen 2008 Temel Ekonometri Literatur Yayinlari ISBN 975 7860 99 9 Audi R Ed 1996 Curve fitting problem The Cambridge Dictionary of Philosophy Cambridge Cambridge University Press pp 172 173 Ingilizce and Judith M Tanur ed 1978 Linear Hypotheses International Encyclopedia of Statistics Free Press cilt 1 Ingilizce Evan J Williams I Regression say 523 41 II Analysis of Variance pp 541 554 1987 Regression and correlation analysis Cilt 4 say 120 23 Ingilizce Birkes David and Yadolah Dodge Alternative Methods of Regression ISBN 0 471 56881 3 Ingilizce Chatfield C 1993 Calculating Interval Forecasts Journal of Business and Economic Statistics 11 pp 121 135 Ingilizce Dincer F Regresyon Kelimesinin Tarihi 1 20 Mayis 2008 tarihinde Wayback Machine sitesinde Draper N R ve Smith H 1998 Applied Regression Analysis Wiley Series in Probability and Statistics Ingilizce Fox J 1997 Applied Regression Analysis Linear Models and Related Methods Sage Ingilizce Hardle W Applied Nonparametric Regression 1990 ISBN 0 521 42950 1 Ingilizce Meade N ve T Islam 1995 Prediction Intervals for Growth Curve Forecasts Journal of Forecasting 14 say 413 430 Ingilizce Munro Barbara Hazard 2005 Statistical Methods for Health Care Research 5th ed Lippincott Williams amp Wilkins Ingilizce Sykes A O Innaugural Coase Lecture Kotsiantis S Kanellopoulos D ve Pintelas P 2006 Local Additive Regression of Decision Stumps Lecture Notes in Artificial Intelligence Springer Verlag Vol 3955 SETN 2006 say 148 157 Ingilizce Kotsiantis S ve Pintelas P 2005 Selective Averaging of Regression Models Annals of Mathematics Computing amp TeleInformatics Cilt 1 No 3 say 66 75 Ingilizce Dis baglantilarWikimedia Commons ta Regresyon analizi ile ilgili ortam dosyalari bulunmaktadir Regresyon analizi12 Nisan 2009 tarihinde Wayback Machine sitesinde Curvefit A complete guide to nonlinear regression21 Temmuz 2009 tarihinde Wayback Machine sitesinde Online ders kitabi Dogrusal model uzerine yorumlar2 Temmuz 2010 tarihinde Wayback Machine sitesinde Bill Venbables tarafindan bazi dogrusal regresyon modelleri uzerinde birkac yorum Dogrusal regresyon icin ornek Dogrusal regresyon denkleminin varyanslarin standart hatalarin korelasyon katsayisinin belirleme katsayisinin ve guvenlik araliklarinin nasil bulundugunu gostermektedir Zayif korelasyon baglantili verilerin regresyonu14 Mart 2010 tarihinde Wayback Machine sitesinde Y araligi X araligindan cok daha kucuk olursa nasil regresyon hatalari ortaya cikabilir xuru org11 Nisan 2010 tarihinde Wayback Machine sitesinde Online regresyon avadanligi Aktif ogrenme Model secimi Vekil modeli regresyonu icin Matlab yazilimi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State























