Doğrusal programlama

Matematik biliminde, özellikle yöneylem araştırması uygulamalı dalında, doğrusal programlama problemleri bir doğrusal eşitlik ve/veya eşitsizlik nı sağlayacak şekilde optimizasyon (yani amaç fonksiyonu değerinin en küçüklenmesi veya en büyüklenmesinin) yapılmasıdır. Bir eğer ve tek bir doğrusal amaç fonksiyonuna sahipse ve tüm kısıtlamaları doğrusal eşitlik veya eşitsizliklerden oluşuyorsa, (lineer) program olarak adlandırılır. Başka bir deyişle, modelin tek-amaçlı fonksiyonu ve tüm kısıtlamaları, süreklilik gösteren ağırlıklı toplamlarından oluşmalıdır.

Doğrusal (lineer) programlamadaki doğrusal (lineer) sözcüğü, modeldeki tüm matematiksel fonksiyonların doğrusal (lineer) olması gerektiğini belirtir. Programlama kelimesi ise bilgisayar programlama'ya işaret etmez; daha çok planlama ile eş anlamlıdır. Dolayısıyla doğrusal (lineer) programlama, birçok uygun alternatif arasından belirlenmiş bir hedefe uyan optimal çözümü bulacak aktivitelerin planlanmasını içerir.

Fazla matematiksel olmayan terimler ile, bir seri doğrusal eşitlik veya eşitsizlik şeklinde ifade edilmiş koşullara bağlı olarak (en küçük maliyet veya en büyük kâr gibi) en iyi sonuca varılmasıdır.

Matris notasyonu kullanılarak

maks ${\displaystyle \mathbf {c} ^{T}\mathbf {x} }$

sk ${\displaystyle A\mathbf {x} \leq \mathbf {b} }$

${\displaystyle \mathbf {x} \geq 0}$

Burada

${\displaystyle \mathbf {c} }$ amaç fonksiyonu katsayılarını (1xn) kapsayan vektördür ve T-üstü transpoz notasyonu olup

${\displaystyle \mathbf {x} }$ değişkenleri kapsayan bir (1xn) vektördür.

${\displaystyle \mathbf {A} }$ bir (mxn) katsayılar matrisidir.

${\displaystyle \mathbf {b} }$ (mx1) sol-tarafta olan sabit değerler vektörüdür.

Genel olarak bir doğrusal programlama probleminde ${\displaystyle \mathbf {b} }$, ${\displaystyle \mathbf {A} }$ ve ${\displaystyle \mathbf {b} }$ matrislerinde sayısal değerler halinde problem başlangıcında verilir ve ${\displaystyle \mathbf {x} }$ vektörü için sayısal değişken değerleri sonuç olarak, problem çözülmekle, bulunur.

Doğrusal programlama birçok pratik alanda kullanım sahası bulmaktadır. Özellikle birçok işletme ve ekonomi sorunlarına özel veya kamu sektöründe devamlı kullanılmaktadır. Nakliyat, enerji üretimi ve dağıtımı, telekomunikasyon, sınai üretim gibi teknik işletmecilik gerektiren alanlarında bulunan birçok firmalar doğrusal programlamayı çok kullanmaktadırlar. Doğrusal programlama işletmecilik alanlarında çok kapsamlı ve çok çeşitli sorunların çözülebilmesini sağlamaktadır. Bunlar sorunlar arasında planlama, yol gösterme, zaman programlaması, iş ve işçi tahsis edilmesi gibi önemli sorunlar doğrusal programlama kullanılarak modellenebilmektedir.

Doğrusal programlamanın tarihçesi

1975, Leonid Kantorovich

Doğrusal eşitsizlikler sistemi şeklindeki bir problemin incelenmesi ta Fourierin çalışmalarına kadar dayanmaktadır ve bu tanınmış matematikçi anısına yöntemi şeklinde isimlendirilmiştir.

1920'lerde Sovyet Rusya'da tüm ekonomi planlaması konuları pratikte ön plana geçmişken teorik olarak tüm ekonominin nasıl planlanabileceğini göstermek için yapılan teorik çalışmalar arasında Leonid Kantoroviç'in katkısı ilk defa bir doğrusal programlama probleminin açıkça ortaya çıkarılmasına yol açmıştır. Ne yazık ki teorinin pratik planlamaya uygulanmasının imkânsızlığı ve ideolojik nedenler dolayısıyla Kantroviç'in bu çalışmasının önemi ancak II. Dünya Savaşından sonra anlaşılabilmiştir.

II. Dünya Savaşı sırasında Birleşik Amerika'da ortaya çıkan lojistik tahsis sorunlarını incelemek için kurulan bir araştırma grubu, grup başkanı olan George Dantzig etrafında, bu türlü sorunların çözülmesi için doğrusal programlama probleminin tanımlanması gereğini ortaya çıkartmışlar ve bu türlü doğrusal programlama problemlerinin çözümü için simpleks algoritması adını verdikleri bir çözüm sistemi ortaya atmışlardır. Özelikle bu matematik modelin ve çözüm algoritmasının, maliyetleri ve getirileri planlama suretiyle harp masraflarının kısılmasına yol açtığı açıkça görüldüğü için bu teorik ve pratik gelişmeler 1947'ye kadar devlet sırı olarak saklı kalmıştır. 1947'de John von Neumann, özellikle oyunlar teorisi ile de ilgileniyorken, geliştirmiştir.

Bu zaman kadar doğrusal programlamaya yaptıkları katkılar nedeni ile Kantoroviç, Dantzing ve von Neumann'a 1975'te verilmiştir.

1947'den sonra özellikle geliştirilen bilgisayar uygulamaları ile birlikte özellikle büyük özel sanayi birimleri ve büyük devlet projeleri için birçok doğrusal programlama problem tanımlanmış ve simpleks algoritması ile çözülüp pratikte kullanılmaya başlanmıştır. Örneğin petrol rafine şirketlerinin günlük üretim planlamaları ve çok girdili ve çok çıktılı üretim karışımı planlamaları için doğrusal programlama çözümlerini devamlı olarak kullanmaya başlamışlardır.

1979'da doğrusal programlama probleminin polinom zaman içinde çözülebileceğini ilk defa ispat etmiştir. Fakat bu alanda çok daha önemli teorik ve pratik gelişmeler 1984'te 'ın doğrusal programlama problemlerin çözülmesi için (simpleks algoritması yerine) ortaya atması ile başlamıştır.

Doğrusal programlamanın pratik yararlılığı bu yöntemin ilk kullanılma problemlerinden biri olan ve Dantzig tarafından ortaya atılan 70 kişinin 70 göreve, karar verici kuruma en iyi sonuç çıkaracak şekilde, tahsis edilmesi örneğinin biraz daha ayrıntılarına bakmak suretiyle anlaşılabilir. Eğer çözüm için her mümkün tahsisi teker teker elden geçirip her biri için amaca yaptığı katkıyı bulmak deneyimine girişilirse, bu kadar çok büyük sayıda permutasyonun elden geçirilmesinin imkânsız olduğu hemen açığa çıkar; çünkü gerekli permütasyon sayısı bütün yakın evrende bulunan parçacıkların sayısına yaklaşır. Eğer bu problem doğrusal programlama şeklinde belirtilip en iyi çözümü bulma kararı verirsek, en zor ve zaman alıcı çabanın probleminin çözümünde değil problemin programa girdisinin hazırlanmasında olduğu anlaşılır. Bu problemin bilgisayarla simpleks algoritması kullanılarak çözülmesi göz kırpma zamanı bile almaz. Doğrusal programlama kuramı arkasında bulunan teori, kontrol edilmesi gereken mümkün en iyi çözüm sayısını çok etkili şekilde azaltmaktadır.

Kullanım alanları

Doğrusal programlama yönteminin çok olmasına rağmen matematik için çok önemli olan optimizasyon alanında çok büyük bir rol oynamasında çeşitli nedenler vardır. Yöneylem araştırması alanında birçok pratik problem doğrusal programlama problemi olarak tanımlanmaktadır. Doğrusal programlamanın bazı özel hallerinin, örneğin ağ şebekelerinde akışım veya çoklu mal akışımı problemlerinin, o kadar önemli oldukları anlaşılmıştır ki özel problem çözüm şekilleri ve algoritmaları ortaya çıkartmak için bu özel problem alanlarına büyük araştırma çabaları yöneltilmiştir.

Diğer tipte olan optimizasyon problemleri için ortaya çıkartılan algoritmaların çoğu özel alt problem olarak doğrusal programlama çözümlerini kapsamaktadır. Matematik optimizasyon kavram ve yöntemlerinin geliştirilmesi için yapılan çalışmaların geçmişine bakılırsa, bunların en önemli olanlarının çoğunun (örneğin dualite, koveksite, bölünebilirlik ve daha genelleştirmeler) ilk defa doğrusal programlama için ortaya atılıp geliştirildiği aşikar olarak görülmektedir.

Aynı şekilde pratik alanlar olan işletmecilik ve mikroiktisat alanlarında etkin mal ve hizmet üretimi ve arzı için gelirleri maksimum hale getirmek veya maliyet ve masrafları minimum hale getirmek için, doğrusal programlama çok büyük katkılarda bulunmaktadır. Doğrusal programlamanın bu pratik alanlardaki kullanıldığı problemler arasında yiyecek maddelerinin harmanlanması, envanter kontrolü, insan ve makine kaynaklarının en iyi şekilde tahsis edilmeleri, ilan kampanyalarının planlaması, elektrik ve diğer enerji için toptan fiyatlama ve tahsis planlaması vb. bulunmaktadır.

Standart şekil

Bir doğrusal programlama probleminin tanımlanması için en uygun ve alışılmış olan şekline standart şekil adı verilmektedir. Bu standart şekilde bir doğrusal programlama problemi üç özel parçadan oluşmaktadır:

Her doğrusal program problemi bir genel standart doğrusal program problemine (yani kanonik şekille) dönüştürülebilir. Matematiksel olarak bir genel standart doğrusal program problemi basitçe bir şekilde şöyle ifade edilir:

• Amaç fonksiyonu - Bir maksimize edilecek doğrusal amaç fonksiyonu
  • Genel olarak n değişkenli problem için:

maks ${\displaystyle \mathbf {c} ^{T}\mathbf {x} }$ veya

maks ${\displaystyle c_{1}x_{1}+c_{2}x_{2}+\cdots +c_{n}x_{n}}$.

• • Örnek olarak 2 değişkenli problem için:

maksimum bul ${\displaystyle c_{1}x_{1}+c_{2}x_{2}\,}$

• Kısıtlamalar - doğrusal eşitsizlik veya eşitlik halinde kısıtlayıcı koşullar:
  • Genel olarak n değişkenli m kısıtlamalı problem için:

sk ${\displaystyle A\mathbf {x} \leq \mathbf {b} }$

veya

${\displaystyle a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}\leq b_{1}}$

${\displaystyle a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}\leq b_{2}}$

......................................................................

${\displaystyle a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}\leq b_{m}}$

• • Örnek olarak 2 değişkenli ve 3 kısıtlamalı problem için

${\displaystyle a_{11}x_{1}+a_{12}x_{2}\leq b_{1}}$

${\displaystyle a_{21}x_{1}+a_{22}x_{2}\leq b_{2}}$

${\displaystyle a_{31}x_{1}+a_{32}x_{2}\leq b_{3}}$

• Negatif olmama kısıtlamaları - sonuç değişken değerlerinin 0 veya pozitif değerde olmaları:
  • Genel olarak n değişkenli problem için:

${\displaystyle \mathbf {x} \geq 0}$

veya

${\displaystyle x_{1}\geq 0}$, ${\displaystyle x_{2}\geq 0}$ ..... ${\displaystyle x_{n}\geq 0}$

• • Örnek olarak 2 değişkenli problem için

${\displaystyle x_{1}\geq 0}$ ve ${\displaystyle x_{2}\geq 0}$

Bu problem kolaylıkla dönüştürülebilir:

maksimum bul: maks. ${\displaystyle \mathbf {c} ^{T}\mathbf {x} }$

kısıtlamalar: kis. ${\displaystyle \mathbf {A} \mathbf {x} \leq \mathbf {b} ,\,\mathbf {x} \geq 0}$

Doğrusal programlama diğer şekiller de alabilir. Bunlardan birkaç örnek verelim: minimizasyon problemleri; değişik şekillerde (${\displaystyle \geq }$ veya = halinde) verilen kısıtlamalar; negatif değişken kapsayan problem vb. Bütün bu değişik şekiller uygun dönüşümler kullanılarak standart forma dönüştürülebilirler.

Örneğin

Eklenmiş şekil (belirtisiz gevşek şekli)

Simpleks algoritmasını kullanıp çözüm bulunmaya başlanmadan önce doğrusal programlama problemlerinin eklenmiş şekle dönüştürülmeleri gerekir. Bu şekil için (≤ şeklinde) eşitsizlik halinde olan her kısıtlama bir negatif olmayan eklenmesi ile eşitlik haline dönüştürülür. Bu halde, doğrusal programlama problemi şu şekli alır:

Z in maksimumunu bulun .

Kısıtlamalar:

${\displaystyle {\begin{bmatrix}1&-\mathbf {c} ^{T}&0\\0&\mathbf {A} &\mathbf {I} \end{bmatrix}}{\begin{bmatrix}Z\\\mathbf {x} \\\mathbf {x} _{s}\end{bmatrix}}={\begin{bmatrix}0\\\mathbf {b} \end{bmatrix}}}$

${\displaystyle \mathbf {x} ,\,\mathbf {x} _{s}\geq 0}$

Burada x_s yeni olarak ortaya çıkartılan gevşeklik değişkenleridir ve Z maksimum değeri bulunacak amaç değişkenidir.

Örneğin

İkincillik

Her dogrusal programlama problemi (ki buna asılsal (primal) problem adı verilir) belirli dönüşümler yapılarak bir diğer probleme çevrilebilir. Bu ikincil problem asılsal probleminin en iyi optimal değeri için bir üst sınır temin eder. Matris şekille asılsal problem standart şekilde şöyle ifade edilir:

Maksimum değer bul - maks. ${\displaystyle \mathbf {c} ^{T}\mathbf {x} }$

Kısıtlamalar - kıs. ${\displaystyle \mathbf {A} \mathbf {x} \leq \mathbf {b} ,\,\mathbf {x} \geq 0}$

Bu asıl belirtilme şekli olan asılsal problemine karşıt ikincil problem matris olarak şöyle yazılır:

Minimum değer bul - min. ${\displaystyle \mathbf {b} ^{T}\mathbf {y} }$

Kısıtlamalar - kıs. ${\displaystyle \mathbf {A} ^{T}\mathbf {y} \geq \mathbf {c} ,\,\mathbf {y} \geq 0}$

Görüldüğü gibi asılsal problemde değişkenler x vektörüyle, ikincil problemde ise y vektörü ile ifade edilmektedir.

İkincillik kuramına iki genel fikir temel olmaktadır. Birine göre ikincil (dual) probleminin tekrar ikincil problemini ortaya çıkartırsak, bunun asılsal problemi olacağı gerçeğidir. İkinci ana fikir ise, bir asılsal doğrusal programlama problemi için her bir uygun çözümün bunun ikincil problemin amaç fonksiyonunun en iyi optimal değerine bir sınır getirdiğidir. Zayıf ikincillik teoremi, bir ikincil problemi için herhangi bir uygun çözümde bulunan amaç fonksiyonu değerinin, bu uygun çözümde asılsal problemi için amaç fonksiyonu değerinden her zaman daha büyük veya eşit olacağını önerir. Güçlü ikincillik teoremi ise eğer asılsal problemi için en iyi optimal çözüm, x* olarak bulunursa, o halde ikincil problem için de bir en iyi optimal çözüm, y*, bulunduğunu ve bu iki optimal çözüm arasında şu bağlantı olduğunu

c^Tx*=b^Ty*

önerir.

Bir doğrusal programlama problemi sınırsız veya uygunsuz bulunarak çözümsüz olabilir. İkincillik teoremine göre, eğer asılsal sınırsız ise, o halde zayıf ikincillik teoremine göre, ikincil problem uygunsuzdur. Aynı şekilde, eğer ikincil problem sınırsız ise, asılsal problem uygunsuz olacaktır. Ancak hem asılsal ve hem de ikincil problemlerinin uygunsuz olmaları da mümkündür.

Örneğin

Tamamlayıcı gevşeklik

Eğer sadece birincil problem için en iyi optimal çözüm biliniyorsa, ikincil problem için bir en iyi optimal çözümün elde edilmesi tamamlayıcı gevşeklik teoremini kullanmak suretiyle mümkün olur. Bu teorem şunu önerir:

x = (x₁, x₂, . . ., x_n) birincil problem için olanaklı bir çözüm ve y = (y₁, y₂, . . ., y_m) ise ikincil problem için olanaklı bir çözüm olduğu kabul edilsin. (w₁, w₂, . . ., w_m) birincil problem icçin gevşeklik değişkenler ve (z₁, z₂, . . ., z_n) du bunlara karşıt ikincil problem için gevşeklik değişkenleri olsunlar. Bu halde x ve y kendileri için yukarıda anılmış problemler için en iyi optimal sonuç olmalariı, ancak ve ancak x_jz_j = 0, for j = 1, 2, . . ., n, w_iy_i = 0, for i = 1, 2, . . ., m. şartları gerçekleşirse ortaya çıkar.

Bu nedenle, eğer birincil problemdeki i'inci gevşeklik değişkeni sıfıra eşit değilse, ikincil problemde i'inci değişken değeri sıfıra eşit olur. Benzer şekilde, eğer ikincil problemdeki j'inci gevşeklik değişken sıfıra eşit değillerse, birincil problemde j'inci değişken değeri sıfıra eşittir.

Kuram

Geometrik olarak, doğrusal kısıtlayıcılar adı verilen bir polihedron belirtirler. Hedef fonksiyonu da doğrusal olduğu, yani bir konveks fonksiyon olduğu, için her yöresel en iyi optimum noktası, otomatik olarak, global en iyi optimal noktası olur. Bu öneri uygulanmasına göre gerçekleşir. Hedef fonksiyonunun doğrusal olması en iyi optimal çözümlerin sonlu noktalar setinin bir ve çok defa tek bir noktadan oluşur.

En iyi optimal çözüm noktasının bulunamadığı iki özel hal bulunmaktadır. Birinci özel halde, kısıtlamalar birbirleri ile tamamiyle çelişme halindedirler (Tam çelişme halindeki iki doğrusal kısıtlamaya örnegin x ≥ 2 ve x ≤ 1 olabilir). Bu halde boştur ve hiçbir çözüm bulunmadığı için en iyi optimal sonuç da yoktur. Bu halde, doğrusal programlama problemine olanaksız problem adı verilir.

Algoritmalar

İki değişken üzerinde bir seri doğrusal kısıtlamalar bu değişkenler için her mümkün çözüm noktasını kapsayan bir 'uygunluk alanı' ortaya çıkarırlar. Çözümü elde edilebilir problem için 'uygunluk alanı' bir şeklini alır.

Doğrusal programlama problemlerinin pratik olarak çözümlenmesi için ilk kullanışlı algoritma George Dantzig ve Rand Corp. özel araştırma ekibinin ortaya attığı simpleks algoritmasıdır. Bu algoritma kısıtlamalardan ortaya çıkan düzeyleri birçok değişirli polihedron (iki değişkenli problemde "uygunluk alanı") olarak görmekte ve bu polihedronda kesişme noktalarını yani polihedron köşelerini (iki değişkenli problemde kısıtlama çizgilerinin kesişme noktalarını) birer mümkün çözüm olarak görmektedir. Bundan sonra bir köşeden başlayıp bu köşeyi tayin eden kenarlar takip edilerek amaç fonksiyonun iyileşmesini sağlayan kenarlar teşhis edilmekte; bunlardan amaç fonksiyonuna en iyi sonuç çıkaracak kenar takip edilip bir diğer polihedron köşesi bulunmaktadır. Bu yeni bulunan polihedron köşesi de aynı usul kullanılarak daha iyi bir başka köşeye gidebilme imkânı aranmaktadır. Eğer elde bulunan bir polihedron köşesinden daha iyi amaç sonuç sağlayan bir köşeye gitme imkânı yoksa, bu son köşe optimum çözüm olarak kabul edilmektedir.

Genel olarak çok büyük sayıda değişkenli ve çok büyük sayıda kısıtlamalı pratik doğrusal programlama problemlerinde bu polihedron üzerinde köşeden köşeye gidiş yönteminin, eğer köşeden köşeye gidişlerin "dalgalanma"larını önlemek için özel itina gösterilirse, etkin ve global bir optimum sonuç çıkartmakta olduğu eldeki kullanma tecrübelerinden bilinmektedir. Fakat matematikçiler bilmektedirler ki bu çeşit yinelemeli (itiratif) çözüm çok büyük sayıda (hatta, üssel olarak artan sayıda) köşe incelemesi gerektirebilmektedir. Önceleri bilgisayar kullanarak bu çeşit yinelemeli çözüm problemlerinin sonlu bir zaman döneminde çözümlenemeyeceği (yani bu problemin P-karmaşıklık sınıfına dahil olduğu) şüphesi ortaya çıkmıştı. Fakat bu soruna yanıt, 1979'da "Leonid Khachiyan" adlı bir Sovyet Rus matematikçisi tarafından geliştirilen ve lineer programlama için ilk en-fena-halde-polinom-zaman algoritması olan 'nin ortaya atılması ile açıklığa kavuşturulmuştur. Buna göre, n tane değişkeni olan ve L girdi "bit"leri ile enkodlanabilen bir problemin çözümlenmesi için, bu Khachiyan algoritması için O(L) sayısal rakamlı O(n⁴L) aritmetik operasyon yapılması gerekmektedir. Bu çözümleme algoritması ("Arkadi Namirovski" tarafından önerilen "konveks optimizasyon" bulunması için kullanılan elipsoid tekniğinin), "Naum Shor" ve "D. Yudin" tarafından geliştirilmiş şekli ile uygulanmaktadır.

Fakat bu yeni algoritma doğrusal programlama üzerinde yeni matematiksel araştırmalara ilham kaynağı olmuş ve matematikçiler polihedronun sınırlarında dışından köşe köşe araştırmaya dayanan "dışsal çözüm"ler arama yerine polihedronun içinden gidişle en iyi dış koşeyi bulmaya dayanan "içsel nokta yöntemleri"ne dayanan algoritmalarla pratik çözüm usulleri geliştirmişlerdir. 1984'te "N.Karmarkar" bir "içsel nokta yöntemi" olarak doğrusal programlama problemlerinin çözümü için 'nı ortaya atmıştır. Bu algoritma ile Khachiyan'ın teorik en-kötü-hal-polinom sınırı 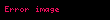${\displaystyle O(n^{3.5}L)}$ ifadesine düşürülmüştür. Böylece simpleks algoritmasına nazaran pratik çözüm performansında gelişmeler ortaya çıkmıştır.

Uy

Hala çözülememiş problemler ve en son çalışmalar

Tam sayılı bilinmeyenler

Uygulama Alanları

Dogrusal programlama pratik hayatta orta dönem veya uzun dönem optimizasyon problemlerinin (yani yoneylem araştırması terimlerini kullanırsak özel sektor veya devlet sektörü kurumlarının taktik ve stratejik problemlerinin) çözülmesi için uygulanmaktadır. Doğrusal programlamanın uygulanma alanı çok geniştir; girdi planlaması, üretim planlaması ve idaresi, insan kaynakları planlaması, dağıtım ve lojistik planlaması ve idaresi, pazarlama planlaması, finansman idaresi ve kontrolü alanlarında özellikle etkin sonuçlar ortaya çıkarırlar. Özellikle büyük tarım üretimi, ormancılık, sanayi sektörü; fabrika üretimi; petrol, gaz, elektrik, nükleer gibi enerji üretimi ve dağıtımı; kara nakliyat vasıtaları, demiryolu ve hava nakliyatı, telekomünikasyon, finansman sağlama vb kesimlerde kullanılmaktadır.

Petrol sanayiinde uygulamalar

Çözücüler ve Scripting (Programlama) Dilleri

• GAMS
• LiPS 6 Haziran 2011 tarihinde Wayback Machine sitesinde .
• Mathematica

Ayrıca bakınız

• Dinamik programlama
• Simpleks algoritması, Doğrusal programlama çözüm algoritması
• Leonid Kantoroviç, Dogrusal programlamayı ilk ortaya atanlardan biri
• Gölge fiyat
• Institute for Operations Research and the Management Sciences ([Amerikan] Yöneylem Araştırması ve İşletme Bilimleri Enstitüsü)

Kaynakça

• Alexander Schrijver, Theory of Linear and Integer Programming. John Wiley, 1998, (İngilizce)
• , , ve . , Second Edition. MIT Press and McGraw-Hill, 2001. . Chapter 29: Linear Programming, pp. 770–821.
• ve (1979). . W.H. Freeman. .  A6: MP1: INTEGER PROGRAMMING, s. 245 (İngilizce)
• Bernd Gärtner, Jiri Matousek (2006). Understanding and Using Linear Programming, Berlin: Springer. (İngilizce)
• V. Chandru and M.R.Rao, Linear Programming, Bölüm 31 Handbook of Algorithms and Theory of Computing, editör M.J.Atallah, CRC Press 1999, 31-1 ile 31-37 arası. http://www.cse.iitb.ac.in/dbms/Data/Papers-Other/Algorithms/lp.ps.gz^[](İngilizce)
• V. Chandru and M.R.Rao, Integer Programming, Bölum 32 in Handbook of Algorithms and Theory of Computing, editor M.J.Atallah, CRC Press 1999, 32-1 ile 32-45 arası. http://citeseer.ist.psu.edu/291576.html 3 Nisan 2008 tarihinde Wayback Machine sitesinde . (İngilizce)
• Michael J. Todd (Şubat 2002). "The many facets of linear programming". Mathematical Programming. 91 (3). (İngilizce)
• , , Mark Overmars, (2000). Computational Geometry (2nd revised edition bas.). Springer-Verlag. . KB1 bakım: Birden fazla ad: yazar listesi () KB1 bakım: Fazladan yazı () Bölüm 4: Doğrusal Programlama: pp. 63–94. Doğrusal programlama için olasılaştırılmış yarı-düzey kesişimi algoritmasını açıklar. (İngilizce)
• Jalaluddin Abdullah, Optimization by the Fixed-Point Method, Version 1.97. http://www.optimization-online.org/DB_HTML/2007/09/1775.html 3 Şubat 2010 tarihinde Wayback Machine sitesinde . (İngilizce)

Dış bağlantılar

• Doğrusal programlama problemlerinin formüle edilmesi 4 Eylül 2009 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişim tarihi:17.4.2009)
• Gizli optimal çözümleri ile birlikte 0-1 tamsayılı programlama kalite testleri 5 Mayıs 2009 tarihinde Wayback Machine sitesinde . (İngilizce)(Erişim tarihi:17.4.2009)
• Doğrusal Programlama 11 Haziran 2008 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişim tarihi:17.4.2009)
• Mathematik programları sözlüğü 28 Mart 2010 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişim tarihi:17.4.2009)
• Tamsayılı programlama üzerine bir derS 5 Eylül 2009 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişim tarihi:17.4.2009)
• (İngilizce) (Erişim tarihi:17.4.2009)
• (İngilizce) (Erişim tarihi:17.4.2009)
• Doğrusal programlama: Formüle edilme, simpleks algoritması, hedef programlaması ve Excel Solver örnekleri 4 Haziran 2009 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişim tarihi:17.4.2009)
• George Dantzig 16 Nisan 2009 tarihinde Wayback Machine sitesinde . (İngilizce)(Erişim tarihi:17.4.2009)

Yazılımlar

• AIMMS Optimization Modeling 3 Şubat 2008 tarihinde Wayback Machine sitesinde . — doğrusal programlamayı pratik sanayide kullanmak üzere tescilli yazılım olarak hazırlanmıştır. Deneme için özel ücretsiz kullanma linansı alınabilir.
• CGAL — Computational Geometry Algorithms Library (Hesaplamak icin Geometri Algoritma Kitapligi) bir doğrusal çözücü kapsar ve nispeten küçük sayıda kısıtlamalar veya değişkenler için kesin sonuçlar verir.
• COIN-OR 19 Aralık 2008 tarihinde Wayback Machine sitesinde . — COmputational INfrastructure for Operations Research, Açık kaynak kitaplığı.
• GAMS 20 Ağustos 2009 tarihinde Wayback Machine sitesinde . — Genel cebirsel modelleme sistemi.
• — Doğrusal programlama çözümleri için satışa hazır programlar.
• GLPK 11 Nisan 2008 tarihinde Wayback Machine sitesinde . — GNU doğrusal programlama için avadanlık: açık kaynaklı ücretsiz doğrusal programlama yazılımları
• HOPDM 3 Şubat 2008 tarihinde Wayback Machine sitesinde . — Yüksek derecede birincil-ikincil yöntemi
• LINDO 23 Mart 2008 tarihinde Wayback Machine sitesinde . — LP, IP, Global çözücü/modelleme dili ile
• lp_solve 15 Mart 2008 tarihinde Wayback Machine sitesinde . — C-kütüphanesi kapsayan açık-kaynaklı çözücü.
• MOSEK 18 Aralık 2008 tarihinde Wayback Machine sitesinde . — LP,IP,QP,SOCP ve MIP için optimazisyon yazılımları.
• Mathematica 17 Şubat 2011 tarihinde Wayback Machine sitesinde . — Genel teknik matematiksel bilgisayar sistemi. Buyuk ölçekte dogrusal programlama çözümü desteği sağlamayı da kapsar.
• Premium Solver 26 Mart 2008 tarihinde Wayback Machine sitesinde . — Kutuçizim için add-in.
• What's Best! 23 Mart 2008 tarihinde Wayback Machine sitesinde . — Kutuçizim için add-in.
• Xpress-MP 29 Mart 2008 tarihinde Wayback Machine sitesinde . — Eğitim için ücretsiz kullanılabilir optimazisyon yazılımı.
• QSopt 28 Mart 2008 tarihinde Wayback Machine sitesinde . Doğrusal programlama optimizasyon yazılımı.
• Doğrusal programlama ve doğrusal amaç programlama problemleri icin MS-DOS kullanan bir 'freeware' program^[]
• GLPK üzerinde IBM tarafından Doğrusal Programlamaya giriş hakkında bir teknik makale 9 Mayıs 2008 tarihinde Wayback Machine sitesinde .
• Orstat2000 11 Nisan 2008 tarihinde Wayback Machine sitesinde . — Doğrusal ve doğrusal-olmayan programlama için kolay kullanılır modülleri kapsar (eğitim amaçlı kullanış için ücretsiz)
• İçinde birkaç doğrusal ve doğrusal-olmayan programlama çözümüleri kapsayan bir bilimsel avadanlık seti.
• TOMLAB 14 Mart 2008 tarihinde Wayback Machine sitesinde . MATLAB, LabVIEW ve .NET yazılm sekillerinde optimizasyon çözücüleri vermektedir.
• SCIP 2 Ekim 2006 tarihinde Wayback Machine sitesinde . MPS dosya formatı veri kullanarak karışık tam sayılı programlama problemlerini tek başına çözümlemek için kompüter programı.
• GIPALS32.DLL 25 Mart 2008 tarihinde Wayback Machine sitesinde . — Windows içinden çağrılabilir doğrusal programlama yazılım kitaplığı (ücretsiz deneyim ve akademik kullanma için özel lisans verilebilir).