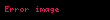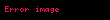Bu maddede bulunmasına karşın yetersizliği nedeniyle bazı bilgilerin hangi kaynaktan alındığı belirsizdir. (Haziran 2016) () |
Matematikte matematiksel programlama, eniyileme ya da optimizasyon terimi; bir gerçel fonksiyonu minimize ya da maksimize etmek amacı ile gerçek ya da tam sayı değerlerini tanımlı bir aralıkta seçip fonksiyona yerleştirerek sistematik olarak bir problemi incelemek ya da çözmek işlemlerini ifade eder. Örneğin bu problem şöyle olabilir:
Verilen: f fonksiyonu: A'dan R ye tanımlı. (R:Reel Sayılar)
Aranan : A'da öyle bir x0 var mı ki; tüm x değerleri için f(x0)≤ f(x)ifadesini sağlasın ("minimizasyon") veya f(x0)≥ f(x) ifadesini sağlasın ("maksimizasyon").
Böylesi bir formulasyona ya da matematiksel programlama problemi denir (terimin bilgisayar programlama ile direkt bir ilgisi yoktur, ama yine de lineer programlamada kullanılan bir ifadedir). Pek çok gerçek ve teorik problemler bu genel çerçevede modellenebilir.Bu teknik kullanılarak formüle edilen problemlere fizik bilminin ilgi alanından bir örnek verilecek olursa, bilgisayar monitörlerinin enerji minimizasyonundan söz edilebilir. O halde, yukarıdaki f fonksiyonu modellenen sistemdeki enerjiyi temsil edecekti.
Bu tür problemlerde "A kümesi" genellikle, bir takım daraltıcı kısıtlar, eşitlikler ve eşitsizlikler ile yerine verilecek(denenecek) değerleri sağlayan (Rn) bir alt kümesidir. f fonksiyonundaki A'nın "arama uzayı", A'nın alacağı değerlerin kümesine ise ya da olası çözümler denir.
f fonksiyouna objektif (nesnel) ya da paha(maliyet) fonksiyonu denir. İstenilen objeyi minimize ya da maksimize eden(amaca göre) olası A çözümüne ise "optimal çözüm" denir.
Genellikle, problemin olası çözümü ve göstermez, birden çok yerel "minimum" ve "maksimum" noktalarına rastlanabilir.
x* da bulunan ve tüm x'ler için δ > 0 iken
- epsilon
ifadesi ile
sağlanıyorsa; x* civarında bir yerlerde fonksiyonun tüm değerlerinin, bu noktadaki değerden büyük veya o'na eşit olduğu söylenebilir, o halde bu nokta bir "" noktasıdır. ( da benzer şekilde ifade edilebilir).
Dışbükey olmayan problemlerin çözümünde pek çok algoritma kullanılmasına rağmen (çoğunlukla ticari amaca yönelik çözüm üreten algoritmalar) yine de yerel optimal noktalar ve gerçek optimal noktaral arasındaki farkların ayırt ve tespit edilmesinde yetersiz kalınmakta ve orijinal probleme bir adım geriden yaklaşılmaktadır. Deterministik algoritmaların gelişimi ile ilgilenip, yakınsayan ve dışbükey olmayan ifadeleri -sınırlı bir zamanda- gerçek bir optimal ifadeye ayrıştırabilen uygulamalı matematik ve nümerik analiz branşlarına global optimizasyon denir.
Başlıca alt dalları
- Doğrusal Programlama : f objektif fonksiyonun doğrusal olduğu ve A kümesinin yalnızca doğrusal eşitlik veya eşitsizlikler ile ulaşılabilir olduğu durumlarda bu isim kullanılır. Böylesi bir A kümesine, sınırlandırılmamış ise polihedron, sınırlı ile politop denir.
- : Doğrusal programların bir ya da daha çok değişkeni tam sayı ile ifade edildiği durumlarda kullanılır.
- : A değeri doğrusal eşitlik veya eşitsizlikler ile gösterilmek kaidesi ile; objektif fonksiyonun değerler almasına müsaade eder.
- : Objektif fonksiyon ya da kısıtların doğrusal olmadığı genel durumları inceler.
- objektif fonksiyon ve kısıtın bir fonksiyon biçiminde ifade edilebileceği durumları inceler. Non-Lineer programlaman özel bir hâli olarak düşünülebilir.
- (SOCP).
- (SDP) Değişkenleri olacak şekilde, bir alt dalıdır. Lineer ve Konveks Kuadratik programlaman genel bir hâlidir.
- : Kısıt ve parametrelerin 'e bağlı olduğu durumları inceler.
- : Optimizasyon problemindeki belirsiz bilgiyi yakalamaya çalışan bir tür stokastik programlamatır.Stokastik programlama gibi, belirsiz bilgiye dayalı olarak çalışmaz ancak problemi girilen bilginin rastgele etkinliği ve şans temelinden kopmadan çözemez.
- : Olası çözüm kümesi içeren problemlerin mümkün ise daha kolay çözülebilir bir şekle indirgenmesi esasına dayanır.
- : Olası çözüm kümesinin (Fonksiyonlar kümesi gibi) sonsuz boyutlu bir uzaya ait olup, olmadığını araştırır.
- f fonskiyonun sabit olup, olamayacağını araştırır (Bu metot yapay zekâ alanında kullanılır, özellikle de konusunda yardımcı olur). kullanularak, seçilen ve önem adledilen (en az) bir kısıtın sağlanması temin edilmesi esasına dayanır.
- : Hava ve uzay araçları için kullanılan özel bir optimizasyon türüdür.
Altdallara göre farklılık gösterecek şekilde, çeşitli teknikler dizayn edilmiştir:
- Objektif fonksiyonun zaman aralıklarından seçilen değişik noktalara nasıl reaksiyon verdiğinin incelenmesi ile kullanılan yöntemdir.
- değişkenler hesabının çeşitli genellemelerinin toplanmış halidir.
- Dinamik programlama Büyük parçaların daha küçük boyutlara indirgenmesi optimizasyon stratejisini yöneten metottur.Bu tür alt problemler ile ilgili olan eşitliklere denir.
Teknikler
İki kez diferansiyeli alınabilen fonksiyonlar için, kısıt bulundurmayan problemler objektif fonksiyonun gradyan'ının sıfır'a eşit olduğu noktaların (istasyon noktaların) yeri tespit edilip, Hesse matrisi ile her noktanın sınıfı belirlenerek çözülebilir.Eğer Hesse pozitif tanımlı ise bu nokta "Yerel Minimum", negatif tanımlı ise "Yerel Maksimum"'dur.Şayet tanımsız ise de bir tür olduğu söylenebilir.
Ancak, her zaman türev almak olası değildir.Objektif fonksiyonun düzgünlüğüne göre metotların ana sınıflandırması şöyle yapılabilir:
Bazı metotlar özel isimleri ile de yukarıdaki dört gruptan birine denk gelecek şekilde listenebilir:
- ya da metodu.
- ya da the Amoeba metodu.
- - Gradyan metodunun, gradyan bulunmayan durumlar için kullanılan hali.
- Newton metodu
- - tek boyulu optimizasyon için kullanılan bir teknik, genellikle başka bir tekniğe yardımcı olması için kullanılır.
Kısıt problemleri genellikle ile kısıttan bağımsız bir forma getirilir.
Birkaç popüler metot daha:
Kullanım alanları
'ne ilişkin problemler sıklık ile matematiksel programlama teknikleri gerektirmektedir.Yapı-Araç İskeleti, manifold ile kısıtlanmış bir 'in çözümüne ihtiyaç duyan bir yönelim olarak değerlendirilebilir.Bu durumda kısıtlar non-lineer olmayan gemotetrik çeşitliliktedir, öneğin "bu iki nokta daima temas etmeli", "bu alan diğerine etki etmemeli" ya da "bu nokta her zaman bu eğri üzerinde olmalı" gibi.Ayrıca temas halindeki kuvvetlere ilişkin problemler de çatısı altında çözüldüğünden, buna da bir tür QP (Kuadratir Programlama) Problemi gözüyle bakılabilir.
Pek çok dizayn problemi de optimizasyon programları ile çözülmektedir.Bu tür uygulamalara denir.Bu alanda bilinen ve büyümekte olan bir alt kol 'dur.Bu tür, pek çok problemde kullanışlı olduğu gibi aynı zamanda da uzay mühendisliği sahasına uyarlanabilmektedir.
Ekonomi de matematiksel programlamaya ağır bir bağımlılık duyar.Mikroiktisat'da sık karşılaşılan bir problem olan marjinal fayda ve bundan kaynaklanan olan iktisadî bir optimizasyon problemidir. Tüketiciler ve firmalar oranlarını maksimize etmek durumundadırlar.Ticaret teorisi de milletler arası ticari ortaklığın izahında optimizasyona sık sık başvurur.
Sabit genel giderli zaman maliyet problemleride önemli bir optimizasyon problemidir. Özellikle inşaat ve endüstri mühendisliğinde bu problemle sıkça karşılaşılır. Doğrusal programlama, sezgisel ve üst sezgisel yöntemler bu problem türünün optimizasyonu için kullanılmaktadır.
Optimizasyon tekniklerinin sıkça kullanıldığı bir diğer alan da 'dır.
Tarihçe
Dik İniş adıyla bilinen ilk optimizasyon tekniğinin tarihi Gauss'a dek uzanır. Tarihi olarak, 1940'larda George Dantzig tarafından ortaya atılan lineer programlama kuramı en yaşlı optimizasyon terimidir. Programlama terimi bu bağlamda 'nı ifade etmez.Program teriminin kullanımı ABD Ordusunun, kendi içtimai ve lojistik takvimini belirlemede konteyner kullandığı "program" terimi ile ilişkilidir. (Daha sonra ise "program" terimi devlet bütçesinin düzenlenmesinde kullanılmış ve günümüzde de yüksek teknolojik araştırmaların sahasına da geçmiştir.)
Optimizasyon Alanına Katkı Sağlayan Diğer Önemli Matematikçiler:
- John von Neumann
- Leonid Vitalyevich Kantorovich
- Leonid Khachian
- Boris Polyak
- Yurii Nesterov
- Arkadii Nemirovskii
- Michael J. Todd
Ayrıca bakınız
Problem Çözücüler
- -NAG kütüphanesi çeşitli problem ve durumlardan oluşan optimizasyona dair geniş bir arşiv sunuyor.http://www.nag.co.uk/optimization/index.asp9 Şubat 2008 tarihinde Wayback Machine sitesinde .
- - Non-Lineer progralama problemlerinin çözümü için geliştirilmiş bir Fortran paketi.http://www.sbsi-sol-optimize.com/asp/sol_product_npsol.htm10 Mart 2008 tarihinde Wayback Machine sitesinde .
- - Pyhton dilinde yazılmış ücretsiz çözücüleri sağlayan bir araç-kutusu
- - Açık kaynak kodlu ilkel-ikincil dahli metotlar ile çalışan bir NLP çözücü.
- - Non-Lineet problemler için bir çözücü.
- Mathematica
- OpenSolver - Açık kaynaklı MS Excel eklentisi olarak çalışan bir çözücü
Kaynakça
- Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. .
- Stephen Boyd and Lieven Vandenberghe (2004). Convex Optimization28 Şubat 2008 tarihinde Wayback Machine sitesinde ., Cambridge University Press. .
- Panos Y. Papalambros and Douglass J. Wilde (2000). Principles of Optimal Design : Modeling and Computation30 Ocak 2008 tarihinde Wayback Machine sitesinde ., Cambridge University Press. .
- Jorge Nocedal and Stephen J. Wright (2006). Numerical Optimization30 Mayıs 2008 tarihinde Wayback Machine sitesinde ., Springer. .
Dış bağlantılar
- şu anda yerine NEOS Wiki[] gelmiş durumda.
- Mathematical Programming Society7 Mart 2006 tarihinde Wayback Machine sitesinde .
- COIN-OR19 Aralık 2008 tarihinde Wayback Machine sitesinde .
- Mathematical Programming Glossary28 Mart 2010 tarihinde Wayback Machine sitesinde .
- Global optimization28 Aralık 2008 tarihinde Wayback Machine sitesinde .
- Optimization Related Links9 Aralık 2008 tarihinde Wayback Machine sitesinde .
- Decision Tree for Optimization Software17 Mart 2007 tarihinde Wayback Machine sitesinde . Optimizasyon kaynak kodlarına linkler içeriyor.
- Optimization Online27 Eylül 2019 tarihinde Wayback Machine sitesinde .
Modeling languages:
- AIMMS23 Temmuz 2019 tarihinde Wayback Machine sitesinde .
- AMPL17 Eylül 2009 tarihinde Wayback Machine sitesinde .
- GAMS20 Ağustos 2009 tarihinde Wayback Machine sitesinde .
Solvers:
- CONOPT23 Aralık 2008 tarihinde Wayback Machine sitesinde .
- - Çok esnek ve açık-kaynak kodlu bir NLP çözücü.
- SAS OR6 Aralık 2008 tarihinde Wayback Machine sitesinde .
- [1]17 Ocak 2008 tarihinde Wayback Machine sitesinde . Stanford Üniversitesi'nin Sistem Optimizasyon Labarotuarı tarafından sunulan ücretsiz optimizasyon yazılımı.
- TANGO Project19 Aralık 2008 tarihinde Wayback Machine sitesinde . Genel Non-Lineer algoritmalar için güvenilir bir yazılım.
- SmartDO22 Ocak 2009 tarihinde Wayback Machine sitesinde . - Mühendislik ile ilgili global optimizasyon yazılımı (ticari)
Kütüphaneler:
- OOL (Open Optimization library)21 Aralık 2008 tarihinde Wayback Machine sitesinde . -
- IOptLib (Investigative Optimization Library)21 Nisan 2008 tarihinde Wayback Machine sitesinde . - (ANSI C).
- ALGLIB7 Aralık 2008 tarihinde Wayback Machine sitesinde . Optimizasyon kaynakları. C++, C#, Delphi, Visual Basic.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede kaynak listesi bulunmasina karsin metin ici kaynaklarin yetersizligi nedeniyle bazi bilgilerin hangi kaynaktan alindigi belirsizdir Lutfen kaynaklari uygun bicimde metin icine yerlestirerek maddenin gelistirilmesine yardimci olun Haziran 2016 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Matematikte matematiksel programlama eniyileme ya da optimizasyon terimi bir gercel fonksiyonu minimize ya da maksimize etmek amaci ile gercek ya da tam sayi degerlerini tanimli bir aralikta secip fonksiyona yerlestirerek sistematik olarak bir problemi incelemek ya da cozmek islemlerini ifade eder Ornegin bu problem soyle olabilir Verilen f fonksiyonu A dan R ye tanimli R Reel Sayilar Aranan A da oyle bir x0 var mi ki tum x degerleri icin f x0 f x ifadesini saglasin minimizasyon veya f x0 f x ifadesini saglasin maksimizasyon Boylesi bir formulasyona ya da matematiksel programlama problemi denir terimin bilgisayar programlama ile direkt bir ilgisi yoktur ama yine de lineer programlamada kullanilan bir ifadedir Pek cok gercek ve teorik problemler bu genel cercevede modellenebilir Bu teknik kullanilarak formule edilen problemlere fizik bilminin ilgi alanindan bir ornek verilecek olursa bilgisayar monitorlerinin enerji minimizasyonundan soz edilebilir O halde yukaridaki f fonksiyonu modellenen sistemdeki enerjiyi temsil edecekti Bu tur problemlerde A kumesi genellikle bir takim daraltici kisitlar esitlikler ve esitsizlikler ile yerine verilecek denenecek degerleri saglayan Rn bir alt kumesidir f fonksiyonundaki A nin arama uzayi A nin alacagi degerlerin kumesine ise ya da olasi cozumler denir f fonksiyouna objektif nesnel ya da paha maliyet fonksiyonu denir Istenilen objeyi minimize ya da maksimize eden amaca gore olasi A cozumune ise optimal cozum denir Genellikle problemin olasi cozumu ve gostermez birden cok yerel minimum ve maksimum noktalarina rastlanabilir x da bulunan ve tum x ler icin d gt 0 iken x x d displaystyle mathbf x mathbf x leq delta epsilon ifadesi ile f x f x displaystyle f mathbf x leq f mathbf x saglaniyorsa x civarinda bir yerlerde fonksiyonun tum degerlerinin bu noktadaki degerden buyuk veya o na esit oldugu soylenebilir o halde bu nokta bir noktasidir da benzer sekilde ifade edilebilir Disbukey olmayan problemlerin cozumunde pek cok algoritma kullanilmasina ragmen cogunlukla ticari amaca yonelik cozum ureten algoritmalar yine de yerel optimal noktalar ve gercek optimal noktaral arasindaki farklarin ayirt ve tespit edilmesinde yetersiz kalinmakta ve orijinal probleme bir adim geriden yaklasilmaktadir Deterministik algoritmalarin gelisimi ile ilgilenip yakinsayan ve disbukey olmayan ifadeleri sinirli bir zamanda gercek bir optimal ifadeye ayristirabilen uygulamali matematik ve numerik analiz branslarina global optimizasyon denir Baslica alt dallariDogrusal Programlama f objektif fonksiyonun dogrusal oldugu ve A kumesinin yalnizca dogrusal esitlik veya esitsizlikler ile ulasilabilir oldugu durumlarda bu isim kullanilir Boylesi bir A kumesine sinirlandirilmamis ise polihedron sinirli ile politop denir Dogrusal programlarin bir ya da daha cok degiskeni tam sayi ile ifade edildigi durumlarda kullanilir A degeri dogrusal esitlik veya esitsizlikler ile gosterilmek kaidesi ile objektif fonksiyonun degerler almasina musaade eder Objektif fonksiyon ya da kisitlarin dogrusal olmadigi genel durumlari inceler objektif fonksiyon ve kisitin bir fonksiyon biciminde ifade edilebilecegi durumlari inceler Non Lineer programlaman ozel bir hali olarak dusunulebilir SOCP SDP Degiskenleri olacak sekilde bir alt dalidir Lineer ve Konveks Kuadratik programlaman genel bir halidir Kisit ve parametrelerin e bagli oldugu durumlari inceler Optimizasyon problemindeki belirsiz bilgiyi yakalamaya calisan bir tur stokastik programlamatir Stokastik programlama gibi belirsiz bilgiye dayali olarak calismaz ancak problemi girilen bilginin rastgele etkinligi ve sans temelinden kopmadan cozemez Olasi cozum kumesi iceren problemlerin mumkun ise daha kolay cozulebilir bir sekle indirgenmesi esasina dayanir Olasi cozum kumesinin Fonksiyonlar kumesi gibi sonsuz boyutlu bir uzaya ait olup olmadigini arastirir f fonskiyonun sabit olup olamayacagini arastirir Bu metot yapay zeka alaninda kullanilir ozellikle de konusunda yardimci olur kullanularak secilen ve onem adledilen en az bir kisitin saglanmasi temin edilmesi esasina dayanir Hava ve uzay araclari icin kullanilan ozel bir optimizasyon turudur Altdallara gore farklilik gosterecek sekilde cesitli teknikler dizayn edilmistir Objektif fonksiyonun zaman araliklarindan secilen degisik noktalara nasil reaksiyon verdiginin incelenmesi ile kullanilan yontemdir degiskenler hesabinin cesitli genellemelerinin toplanmis halidir Dinamik programlama Buyuk parcalarin daha kucuk boyutlara indirgenmesi optimizasyon stratejisini yoneten metottur Bu tur alt problemler ile ilgili olan esitliklere denir TekniklerIki kez diferansiyeli alinabilen fonksiyonlar icin kisit bulundurmayan problemler objektif fonksiyonun gradyan inin sifir a esit oldugu noktalarin istasyon noktalarin yeri tespit edilip Hesse matrisi ile her noktanin sinifi belirlenerek cozulebilir Eger Hesse pozitif tanimli ise bu nokta Yerel Minimum negatif tanimli ise Yerel Maksimum dur Sayet tanimsiz ise de bir tur oldugu soylenebilir Ancak her zaman turev almak olasi degildir Objektif fonksiyonun duzgunlugune gore metotlarin ana siniflandirmasi soyle yapilabilir Bazi metotlar ozel isimleri ile de yukaridaki dort gruptan birine denk gelecek sekilde listenebilir ya da metodu ya da the Amoeba metodu Gradyan metodunun gradyan bulunmayan durumlar icin kullanilan hali Newton metodu tek boyulu optimizasyon icin kullanilan bir teknik genellikle baska bir teknige yardimci olmasi icin kullanilir Kisit problemleri genellikle ile kisittan bagimsiz bir forma getirilir Birkac populer metot daha Genetik algoritmalar Evrim stratejisiKullanim alanlari ne iliskin problemler siklik ile matematiksel programlama teknikleri gerektirmektedir Yapi Arac Iskeleti manifold ile kisitlanmis bir in cozumune ihtiyac duyan bir yonelim olarak degerlendirilebilir Bu durumda kisitlar non lineer olmayan gemotetrik cesitliliktedir onegin bu iki nokta daima temas etmeli bu alan digerine etki etmemeli ya da bu nokta her zaman bu egri uzerinde olmali gibi Ayrica temas halindeki kuvvetlere iliskin problemler de catisi altinda cozuldugunden buna da bir tur QP Kuadratir Programlama Problemi gozuyle bakilabilir Pek cok dizayn problemi de optimizasyon programlari ile cozulmektedir Bu tur uygulamalara denir Bu alanda bilinen ve buyumekte olan bir alt kol dur Bu tur pek cok problemde kullanisli oldugu gibi ayni zamanda da uzay muhendisligi sahasina uyarlanabilmektedir Ekonomi de matematiksel programlamaya agir bir bagimlilik duyar Mikroiktisat da sik karsilasilan bir problem olan marjinal fayda ve bundan kaynaklanan olan iktisadi bir optimizasyon problemidir Tuketiciler ve firmalar oranlarini maksimize etmek durumundadirlar Ticaret teorisi de milletler arasi ticari ortakligin izahinda optimizasyona sik sik basvurur Sabit genel giderli zaman maliyet problemleride onemli bir optimizasyon problemidir Ozellikle insaat ve endustri muhendisliginde bu problemle sikca karsilasilir Dogrusal programlama sezgisel ve ust sezgisel yontemler bu problem turunun optimizasyonu icin kullanilmaktadir Optimizasyon tekniklerinin sikca kullanildigi bir diger alan da dir TarihceDik Inis adiyla bilinen ilk optimizasyon tekniginin tarihi Gauss a dek uzanir Tarihi olarak 1940 larda George Dantzig tarafindan ortaya atilan lineer programlama kurami en yasli optimizasyon terimidir Programlama terimi bu baglamda ni ifade etmez Program teriminin kullanimi ABD Ordusunun kendi ictimai ve lojistik takvimini belirlemede konteyner kullandigi program terimi ile iliskilidir Daha sonra ise program terimi devlet butcesinin duzenlenmesinde kullanilmis ve gunumuzde de yuksek teknolojik arastirmalarin sahasina da gecmistir Optimizasyon Alanina Katki Saglayan Diger Onemli Matematikciler John von Neumann Leonid Vitalyevich Kantorovich Leonid Khachian Boris Polyak Yurii Nesterov Arkadii Nemirovskii Michael J ToddAyrica bakinizOyun teorisi Yoneylem arastirmasi Bulanik mantik Dinamik programlamaProblem Cozuculer NAG kutuphanesi cesitli problem ve durumlardan olusan optimizasyona dair genis bir arsiv sunuyor http www nag co uk optimization index asp9 Subat 2008 tarihinde Wayback Machine sitesinde Non Lineer progralama problemlerinin cozumu icin gelistirilmis bir Fortran paketi http www sbsi sol optimize com asp sol product npsol htm10 Mart 2008 tarihinde Wayback Machine sitesinde Pyhton dilinde yazilmis ucretsiz cozuculeri saglayan bir arac kutusu Acik kaynak kodlu ilkel ikincil dahli metotlar ile calisan bir NLP cozucu Non Lineet problemler icin bir cozucu Mathematica OpenSolver Acik kaynakli MS Excel eklentisi olarak calisan bir cozucuKaynakcaMordecai Avriel 2003 Nonlinear Programming Analysis and Methods Dover Publishing ISBN 0 486 43227 0 Stephen Boyd and Lieven Vandenberghe 2004 Convex Optimization28 Subat 2008 tarihinde Wayback Machine sitesinde Cambridge University Press ISBN 0 521 83378 7 Panos Y Papalambros and Douglass J Wilde 2000 Principles of Optimal Design Modeling and Computation30 Ocak 2008 tarihinde Wayback Machine sitesinde Cambridge University Press ISBN 0 521 62727 3 Jorge Nocedal and Stephen J Wright 2006 Numerical Optimization30 Mayis 2008 tarihinde Wayback Machine sitesinde Springer ISBN 0 387 30303 0 Dis baglantilarsu anda yerine NEOS Wiki olu kirik baglanti gelmis durumda Mathematical Programming Society7 Mart 2006 tarihinde Wayback Machine sitesinde COIN OR19 Aralik 2008 tarihinde Wayback Machine sitesinde Mathematical Programming Glossary28 Mart 2010 tarihinde Wayback Machine sitesinde Global optimization28 Aralik 2008 tarihinde Wayback Machine sitesinde Optimization Related Links9 Aralik 2008 tarihinde Wayback Machine sitesinde Decision Tree for Optimization Software17 Mart 2007 tarihinde Wayback Machine sitesinde Optimizasyon kaynak kodlarina linkler iceriyor Optimization Online27 Eylul 2019 tarihinde Wayback Machine sitesinde Modeling languages AIMMS23 Temmuz 2019 tarihinde Wayback Machine sitesinde AMPL17 Eylul 2009 tarihinde Wayback Machine sitesinde GAMS20 Agustos 2009 tarihinde Wayback Machine sitesinde Solvers CONOPT23 Aralik 2008 tarihinde Wayback Machine sitesinde Cok esnek ve acik kaynak kodlu bir NLP cozucu SAS OR6 Aralik 2008 tarihinde Wayback Machine sitesinde 1 17 Ocak 2008 tarihinde Wayback Machine sitesinde Stanford Universitesi nin Sistem Optimizasyon Labarotuari tarafindan sunulan ucretsiz optimizasyon yazilimi TANGO Project19 Aralik 2008 tarihinde Wayback Machine sitesinde Genel Non Lineer algoritmalar icin guvenilir bir yazilim SmartDO22 Ocak 2009 tarihinde Wayback Machine sitesinde Muhendislik ile ilgili global optimizasyon yazilimi ticari Kutuphaneler OOL Open Optimization library 21 Aralik 2008 tarihinde Wayback Machine sitesinde IOptLib Investigative Optimization Library 21 Nisan 2008 tarihinde Wayback Machine sitesinde ANSI C ALGLIB7 Aralik 2008 tarihinde Wayback Machine sitesinde Optimizasyon kaynaklari C C Delphi Visual Basic
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State