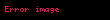Öklid geometrisinde, Droz-Farny doğru teoremi, keyfi bir üçgenin yükseklik merkezinden (ortosantr) geçen iki dik doğrunun bir özelliğidir.

, köşeleri , ve olan bir üçgen ve , yükseklik merkezi (üç yüksekliğin kesiştiği ortak nokta) olsun. ve , üzerinden geçen birbirine dik herhangi iki doğru olsun. , ve sırasıyla 'in , ve kenar doğrularıyla kesiştiği noktalar olsun. Benzer şekilde, , ve de 'nin bu kenar doğrularıyla kesiştiği noktalar olsun. Droz-Farny doğru teoremi, üç doğru parçası , ve 'nin orta noktalarının eşdoğrusal olduğunu ifade eder.
Teorem, tarafından 1899'da dile getirilmiştir ancak bir kanıtı olup olmadığı net değildir.
Goormaghtigh'in genellemesi
Droz-Farny doğru teoreminin bir genellemesi 1930'da tarafından kanıtlandı.
Yukarıdaki gibi 









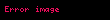
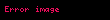











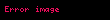

Droz-Farny doğru teoremi, 

Dao'nun genellemesi
Teorem, tarafından daha da genelleştirildi. Genelleme aşağıdaki gibidir:
İlk genelleme: 






İkinci genelleme: Düzlemde bir konik 















Kaynakça
- ^ a b A. Droz-Farny (1899), "Question 14111", The Educational Times, 71, ss. 89-90
- ^ Ayme, Jean-Louis (2004), "A Purely Synthetic Proof of the Droz-Farny Line Theorem", Forum Geometricorum, 14, ss. 219-224, ISSN 1534-1178, 16 Temmuz 2020 tarihinde kaynağından arşivlendi
- ^ Floor van Lamoen; Eric W. Weisstein, "Droz-Farny Theorem", MathWorld, 27 Ekim 2020 tarihinde kaynağından arşivlendi
- ^ O'Connor, John J.; Robertson, Edmund F., "Droz-Farny doğru teoremi", MacTutor Matematik Tarihi arşivi
- ^ René Goormaghtigh (1930), "Sur une généralisation du théoreme de Noyer, Droz-Farny et Neuberg"", Mathesis, cilt 44, s. 25
- ^ Son Tran Hoang (2014), "A synthetic proof of Dao's generalization of Goormaghtigh's theorem", Global Journal of Advanced Research on Classical and Modern Geometries, cilt 3, ss. 125-129, ISSN 2284-5569, 6 Ekim 2014 tarihinde kaynağından arşivlendi
- ^ Nguyen Ngoc Giang, A proof of Dao theorem, Global Journal of Advanced Research on Classical and Modern Geometries, Vol.4, (2015), Issue 2, page 102-105 6 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi., ISSN 2284-5569
- ^ Smith, Geoff (2015). "99.20 A projective Simson line". The Mathematical Gazette (99): 339-341. doi:10.1017/mag.2015.47. 6 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.
- ^ Dao, O.T (29 Temmuz 2013). "Two Pascals merge into one". Cut-the-Knot. 26 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.
Konuyla ilgili yayınlar
- Ayme, Jean-Louis (2004), A Purely Synthetic Proof of the Droz-Farny Line Theorem (PDF), 4, Forum Geometricorum, ss. 219-224, 31 Aralık 2019 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 23 Ekim 2020 veya Alternatif Bağlantı (PDF), 15 Şubat 2020 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 23 Ekim 2020
- Thas, Charles (2006), A Note on the Droz-Farny Theorem, 6, Forum Geometricorum [electronic only]
- Struve, R; Struve, H. (2016), "An axiomatic analysis of the Droz-Farny Line Theorem", Aequat. Math., 90, ss. 1201-1218, doi:10.1007/s00010-016-0430-2
Dış bağlantılar
- "Droz-Farny Line Theorem" (Java Applet). cut-the-knot. 27 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.
- "A generalization of Droz-Farny line theorem". geogebra. 28 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.
- "Goormaghtigh's generalization of the Droz-Farny Line". geogebra. 26 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.
- "Droz-Farny line on a sphere". geogebra. 26 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Oklid geometrisinde Droz Farny dogru teoremi keyfi bir ucgenin yukseklik merkezinden ortosantr gecen iki dik dogrunun bir ozelligidir A0 B0 C0 displaystyle A 0 B 0 C 0 dan gecen dogru Droz Farny dogrusudur T displaystyle T koseleri A displaystyle A B displaystyle B ve C displaystyle C olan bir ucgen ve H displaystyle H yukseklik merkezi uc yuksekligin kesistigi ortak nokta olsun L1 displaystyle L 1 ve L2 displaystyle L 2 H displaystyle H uzerinden gecen birbirine dik herhangi iki dogru olsun A1 displaystyle A 1 B1 displaystyle B 1 ve C1 displaystyle C 1 sirasiyla L1 displaystyle L 1 in BC displaystyle BC CA displaystyle CA ve AB displaystyle AB kenar dogrulariyla kesistigi noktalar olsun Benzer sekilde A2 displaystyle A 2 B2 displaystyle B 2 ve C2 displaystyle C 2 de L2 displaystyle L 2 nin bu kenar dogrulariyla kesistigi noktalar olsun Droz Farny dogru teoremi uc dogru parcasi A1A2 displaystyle A 1 A 2 B1B2 displaystyle B 1 B 2 ve C1C2 displaystyle C 1 C 2 nin orta noktalarinin esdogrusal oldugunu ifade eder Teorem tarafindan 1899 da dile getirilmistir ancak bir kaniti olup olmadigi net degildir Goormaghtigh in genellemesiDroz Farny dogru teoreminin bir genellemesi 1930 da tarafindan kanitlandi Yukaridaki gibi T displaystyle T koseleri A displaystyle A B displaystyle B ve C displaystyle C olan bir ucgen olsun P displaystyle P A displaystyle A B displaystyle B ve C displaystyle C den farkli herhangi bir nokta olsun ve L displaystyle L P displaystyle P uzerinden gecen herhangi bir dogru olsun A1 displaystyle A 1 B1 displaystyle B 1 ve C1 displaystyle C 1 sirasiyla BC displaystyle BC CA displaystyle CA ve AB displaystyle AB kenar dogrulari uzerindeki PA1 displaystyle PA 1 PB1 displaystyle PB 1 ve PC1 displaystyle PC 1 L displaystyle L dogrusuna gore simetrik yansitma yoluyla sirasiyla PA displaystyle PA PB displaystyle PB ve PC displaystyle PC dogrularinin goruntuleri olacak sekilde noktalar olsun Daha sonra Goormaghtigh teoremi A1 displaystyle A 1 B1 displaystyle B 1 ve C1 displaystyle C 1 noktalarinin esdogrusal oldugunu soyler Droz Farny dogru teoremi P displaystyle P T displaystyle T ucgeninin yukseklik merkezi oldugunda bu sonucun ozel bir durumudur Dao nun genellemesiTeorem tarafindan daha da genellestirildi Genelleme asagidaki gibidir Ilk genelleme ABC displaystyle ABC bir ucgen olsun P displaystyle P duzlemdeki bir nokta olsun uc paralel dogru parcasi AA BB CC displaystyle AA BB CC olsun boylece orta noktalar ve P displaystyle P esdogrusal olsun Daha sonra PA PB PC displaystyle PA PB PC sirasiyla uc esdogrusal noktada BC CA AB displaystyle BC CA AB ile kesisir Dao nun ikinci genellemesi Ikinci genelleme Duzlemde bir konik S displaystyle S ve bir P displaystyle P noktasi olsun Konik ile sirasiyla A A displaystyle A A B B displaystyle B B C C displaystyle C C noktasinda kesisecek sekilde P displaystyle P den gecen uc da db dc displaystyle d a d b d c dogrusu olusturun D displaystyle D S displaystyle S ye gore P displaystyle P noktasinin kutup dogrusu uzerinde bir nokta olsun veya D displaystyle D konik S displaystyle S uzerinde yer alir DA BC A0 displaystyle DA cap BC A 0 DB AC B0 displaystyle DB cap AC B 0 DC AB C0 displaystyle DC cap AB C 0 olsun O zaman A0 B0 C0 displaystyle A 0 B 0 C 0 esdogrusaldir Kaynakca a b A Droz Farny 1899 Question 14111 The Educational Times 71 ss 89 90 Ayme Jean Louis 2004 A Purely Synthetic Proof of the Droz Farny Line Theorem Forum Geometricorum 14 ss 219 224 ISSN 1534 1178 16 Temmuz 2020 tarihinde kaynagindan arsivlendi Floor van Lamoen Eric W Weisstein Droz Farny Theorem MathWorld 27 Ekim 2020 tarihinde kaynagindan arsivlendi O Connor John J Robertson Edmund F Droz Farny dogru teoremi MacTutor Matematik Tarihi arsivi Rene Goormaghtigh 1930 Sur une generalisation du theoreme de Noyer Droz Farny et Neuberg Mathesis cilt 44 s 25 Son Tran Hoang 2014 A synthetic proof of Dao s generalization of Goormaghtigh s theorem Global Journal of Advanced Research on Classical and Modern Geometries cilt 3 ss 125 129 ISSN 2284 5569 6 Ekim 2014 tarihinde kaynagindan arsivlendi Nguyen Ngoc Giang A proof of Dao theorem Global Journal of Advanced Research on Classical and Modern Geometries Vol 4 2015 Issue 2 page 102 105 6 Ekim 2014 tarihinde Wayback Machine sitesinde arsivlendi ISSN 2284 5569 Smith Geoff 2015 99 20 A projective Simson line The Mathematical Gazette 99 339 341 doi 10 1017 mag 2015 47 6 Mart 2016 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Ekim 2020 Dao O T 29 Temmuz 2013 Two Pascals merge into one Cut the Knot 26 Ekim 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Ekim 2020 Konuyla ilgili yayinlarAyme Jean Louis 2004 A Purely Synthetic Proof of the Droz Farny Line Theorem PDF 4 Forum Geometricorum ss 219 224 31 Aralik 2019 tarihinde kaynagindan arsivlendi PDF erisim tarihi 23 Ekim 2020 veya Alternatif Baglanti PDF 15 Subat 2020 tarihinde kaynagindan arsivlendi PDF erisim tarihi 23 Ekim 2020 Thas Charles 2006 A Note on the Droz Farny Theorem 6 Forum Geometricorum electronic only Struve R Struve H 2016 An axiomatic analysis of the Droz Farny Line Theorem Aequat Math 90 ss 1201 1218 doi 10 1007 s00010 016 0430 2 Dis baglantilar Droz Farny Line Theorem Java Applet cut the knot 27 Ekim 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Ekim 2020 A generalization of Droz Farny line theorem geogebra 28 Ekim 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Ekim 2020 Goormaghtigh s generalization of the Droz Farny Line geogebra 26 Ekim 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Ekim 2020 Droz Farny line on a sphere geogebra 26 Ekim 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Ekim 2020
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State