Matematik, mĂŒhendislik ve imalat alanlarında kullanılan dönel cisim, bir eÄriyi aynı dĂŒzlemde bulunan bir doÄru (dönme ekseni) etrafında döndĂŒrĂŒlerek elde edilen Ćekildir.

EÄrinin dönme eksenini geçmediÄi kabul edilirse; dönel cismin hacmi, Ćeklin aÄırlık merkezini merkez kabul eden dairenin uzunluÄu ile Ćeklin alanının çarpımıdır ().
Temsili disk dönel cisimin ĂŒĂ§-boyutlu bir . Bu eleman (w uzunluÄunda) bir doÄru parçasının (r birim uzaklıkta) bir eksen etrafında döndĂŒrĂŒlmesiyle oluĆturulur. Böylece Ïr2w birimlik silindirik hacim çevrelenmiĆ olur.
Hacim bulma
Dönel cismin hacmini bulmak için sıklıkla kullanılan iki integrasyon yöntemi, disk yöntemi ve kabuk yöntemidir. Bu yöntemleri uygulamak için, grafik çizmek en kolayıdır; dönme ekseni etrafında döndĂŒrĂŒlecek alan belirlenir; dönel cismin ÎŽx kalınlıÄına sahip disk Ćeklindeki bir diliminin ya da ÎŽx geniĆliÄindeki silindirik bir kabuÄun hacmi bulunur ve bu hacimlerin ÎŽx 0'a yakınsarkenki limit toplamı hesaplanır. Bu limit deÄeri, uygun bir integral hesaplanarak da bulunabilir.
Disk yöntemi

Disk yöntemi, çizilen dilimin dönme eksenine dik olduÄu zaman yani dönme eksenine paralel integrasyon gerçekleĆtirilirken kullanılır.

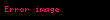


EÄer g(x) = 0 ise (yani bir eÄri ile x-ekseni arasındaki alan döndĂŒrĂŒlĂŒyorsa) formĂŒl Ćöyle indirgenir:
Bu yöntem ĂŒst noktası 




Silindir yöntemi

Silindir yöntemi, çizilen dilimin dönme eksenine paralel olduÄu zaman yani dönme eksenine dik integrasyon gerçekleĆtirilirken kullanılır.

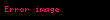


EÄer g(x) = 0 ise (yani bir eÄri ile x-ekseni arasındaki alan döndĂŒrĂŒlĂŒyorsa) formĂŒl Ćöyle indirgenir:
Bu yöntem 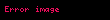
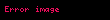

Parametrik form
Bir eÄri 

Aynı Ćartlar altında eÄriyi x-ekseni veya y ekseni etrafında döndĂŒrĂŒlerek oluĆturulan dönel cisimlerin yĂŒzey alanları Ćöyle verilir:
Notlar
Kaynakça
- CliffsNotes.com. Volumes of Solids of Revolution. 12 Apr 2011 <>.
- , . : Calculus. McGraw-Hill Professional 2008, . pp. 244â248 (Google Kitaplar'da online copy, s. 244,)
- Eric W. Weisstein, Solid of Revolution (MathWorld)
- Vikipedi Solid of revolution makalesi. (Son EriĆim Tarihi: 05.04.2015)
wikipedia, wiki, viki, vikipedia, oku, kitap, kĂŒtĂŒphane, kĂŒtĂŒbhane, ara, ara bul, bul, herĆey, ne arasanız burada,hikayeler, makale, kitaplar, öÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tĂŒrk, tĂŒrkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ĂŒcretsiz, ĂŒcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mĂŒzik, Ćarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik muhendislik ve imalat alanlarinda kullanilan donel cisim bir egriyi ayni duzlemde bulunan bir dogru donme ekseni etrafinda dondurulerek elde edilen sekildir Egri donduruluyor Cismi cevreleyen bu yuzey Egrinin donme eksenini gecmedigi kabul edilirse donel cismin hacmi seklin agirlik merkezini merkez kabul eden dairenin uzunlugu ile seklin alaninin carpimidir Temsili disk donel cisimin uc boyutlu bir Bu eleman w uzunlugunda bir dogru parcasinin r birim uzaklikta bir eksen etrafinda dondurulmesiyle olusturulur Boylece pr2wbirimlik silindirik hacim cevrelenmis olur Hacim bulmaDonel cismin hacmini bulmak icin siklikla kullanilan iki integrasyon yontemi disk yontemi ve kabuk yontemidir Bu yontemleri uygulamak icin grafik cizmek en kolayidir donme ekseni etrafinda dondurulecek alan belirlenir donel cismin dx kalinligina sahip disk seklindeki bir diliminin ya da dx genisligindeki silindirik bir kabugun hacmi bulunur ve bu hacimlerin dx 0 a yakinsarkenki limit toplami hesaplanir Bu limit degeri uygun bir integral hesaplanarak da bulunabilir Disk yontemi Y ekseni etrafinda disk integrasyonu Disk yontemi cizilen dilimin donme eksenine dik oldugu zaman yani donme eksenine paralel integrasyon gerceklestirilirken kullanilir f x displaystyle f x ve g x displaystyle g x egrileri ve x a displaystyle x a ve x b displaystyle x b dogrulari arasinda kalan alan x ekseni etrafinda dondurulerek olusan donel cismin hacmi soyle ifade edilir V p ab f2 x g2 x dx displaystyle V pi int a b vert f 2 x g 2 x vert dx Eger g x 0 ise yani bir egri ile x ekseni arasindaki alan donduruluyorsa formul soyle indirgenir V p abf2 x dx 1 displaystyle V pi int a b f 2 x dx qquad 1 Bu yontem ust noktasi f y displaystyle f y alt noktasi g y displaystyle g y olmak uzere yatay olarak uzanan cok ince bir dikdortgen ile gorsellestirilebilir Bu dikdortgen y ekseni etrafinda dondurulurse yuzuk bicimini alir g y 0 displaystyle g y 0 ise disk olur Bu yuzugun dis yaricapi f y ic yaricapi ise g y olur R dis yaricap bu durumda f y r ic yaricap bu durumda g y olmak uzere bu yuzugun alani p R2 r2 displaystyle pi R 2 r 2 dir Araliktaki tum alanlari toplamak toplam hacmi verir Bu yuzden her bir sonsuz kucuk diskin hacmi pf2 x dx displaystyle pi f 2 x dx dir Bu disklerin a ve b araligindaki sonsuz toplami acikca integral 1 seklinde kendini gosterir Silindir yontemi Kabuk integrasyonu Silindir yontemi cizilen dilimin donme eksenine paralel oldugu zaman yani donme eksenine dik integrasyon gerceklestirilirken kullanilir f x displaystyle f x ve g x displaystyle g x egrileri ve x a displaystyle x a ve x b displaystyle x b dogrulari arasinda kalan alan y ekseni etrafinda dondurulerek olusan donel cismin hacmi soyle ifade edilir V 2p abx f x g x dx displaystyle V 2 pi int a b x vert f x g x vert dx Eger g x 0 ise yani bir egri ile x ekseni arasindaki alan donduruluyorsa formul soyle indirgenir V 2p abx f x dx displaystyle V 2 pi int a b x vert f x vert dx Bu yontem f x g x displaystyle f x g x yuksekligine sahip ve dikey olarak uzanan cok ince bir dikdortgen ile gorsellestirilebilir Bu dikdortgen y ekseni etrafinda dondurulurse silindirik kabuk bicimini alir r yaricap bu durumda x h yukseklik bu durumda f x g x displaystyle f x g x olmak uzere bir silindirin yanal alani 2prh displaystyle 2 pi rh dir Araliktaki tum yuzey alanlarini toplamak toplam hacmi verir Parametrik formBir egri x t y t displaystyle x t y t parametrik formunda a b displaystyle a b araliginda tanimlandiginda egriyi x ekseni veya y ekseni etrafinda dondurulerek olusturulan donel cisimlerin hacmi soyle verilir Vx abpy2dxdtdt displaystyle V x int a b pi y 2 frac dx dt dt Vy abpx2dydtdt displaystyle V y int a b pi x 2 frac dy dt dt Ayni sartlar altinda egriyi x ekseni veya y ekseni etrafinda dondurulerek olusturulan donel cisimlerin yuzey alanlari soyle verilir Ax ab2py dxdt 2 dydt 2dt displaystyle A x int a b 2 pi y sqrt left frac dx dt right 2 left frac dy dt right 2 dt Ay ab2px dxdt 2 dydt 2dt displaystyle A y int a b 2 pi x sqrt left frac dx dt right 2 left frac dy dt right 2 dt Notlar Sharma A K 2005 Application Of Integral Calculus Discovery Publishing House s 168 ISBN 81 7141 967 4 Chapter 3 page 168 Singh 1993 Engineering Mathematics 6 Tata McGraw Hill s 6 90 ISBN 0 07 014615 2 Chapter 6 page 6 90KaynakcaCliffsNotes com Volumes of Solids of Revolution 12 Apr 2011 lt gt Calculus McGraw Hill Professional 2008 ISBN 978 0 07 150861 2 pp 244 248 Google Kitaplar da online copy s 244 Eric W Weisstein Solid of Revolution MathWorld Vikipedi Solid of revolution makalesi Son Erisim Tarihi 05 04 2015
 AzÉrbaycanca
AzÉrbaycanca ĐДлаŃŃŃĐșŃ
ĐДлаŃŃŃĐșŃ Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana æ„æŹèȘ
æ„æŹèȘ ÒĐ°Đ·Đ°Ò
ÒĐ°Đ·Đ°Ò Lietuvos
Lietuvos Nederlands
Nederlands PortuguĂȘs
PortuguĂȘs Đ ŃŃŃĐșĐžĐč
Đ ŃŃŃĐșĐžĐč à·à·à¶à·à¶œ
à·à·à¶à·à¶œ àčàžàžàčàžàžą
àčàžàžàčàžàžą TĂŒrkçe
TĂŒrkçe ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ°
ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ° äžćäșș
äžćäșș United State
United State Afrikaans
Afrikaans