Eşdeğerlik İlkesi

Genel görelilik fiziğinde, eşdeğerlik ilkesi, kütleçekimsel kütle ve eylemsiz kütle arasındaki eşdeğerlikle ilgilenen çeşitli kavramlardan biridir. Einstein'in gözlemlerine göre büyük kütleli bir cismin (Örn. Dünya) üzerinde durulduğunda hissedilen kütleçekimsel kuvvet, eylemsiz olmayan (ivmeli) referans çerçevesindeki bir gözlemcinin hissettiği uydurma kuvvetle aynıdır.

Einstein'in Eşdeğerlik İlkesi hakkındaki açıklaması

Biraz düşünüldüğünde eylemsiz kütle ve kütleçekimsel kütlenin eşitliğinin, kütleçekim alanı tarafından ivmelendirilen cismin ivmesinin cismin doğasından bağımsız olduğu iddiası ile denk olduğu görülecektir. Newton’un kütleçekimsel bir alanda hareket için olan formülü tam hali ile yazıldığında

(Eylemsiz Kütle) ${\displaystyle \cdot }$ (İvme) ${\displaystyle =}$ (Kütleçekimsel alanın yoğunluğu) ${\displaystyle \cdot }$ (Kütleçekimsel Kütle)

İvmelenme, cismin doğasından bağımsız olan eylemsiz kütle ve kütleçekimsel kütle arasında sayısal eşitlik olduğu zaman olmaktadır.

— Albert Einstein

Kütleçekim kuramının gelişimi

16. yüzyıl sonları ve 17. yüzyıl başlarında Galileo deneysel olarak yerçekimi tarafından kazandırılan ivmenin ivmelenen cismin kütlesinden bağımsız olduğunu gösterdiğinde Eşdeğerlik ilkesine benzer bir durum ortaya çıkmıştı. Bu bulgular eylemsiz ve kütleçekimsel kütlelerin aynı olduğu kütleçekimsel kurama yol açmıştır. Eşdeğerlik ilkesi tam olarak Albert Einstein tarafından 1907'de cisimlerin Dünya'nın merkezine doğru olan 1g'lik (g= 9,81 m/s² Dünya’nın yüzeyindeki standart kütleçekimsel ivmenin değeridir) ivmelerinin eylemsizce hareket eden cismin, örneğin boş uzayda 1g ile ivmelenen roket, ivmesi ile eşdeğerde olduğunu gözlemlediğinde ortaya atıldı. Einstein bunu:

…kütleçekimsel alan ve buna karşılık gelen referans sisteminin ivmesi arasında tam bir fiziksel eşdeğerlik olduğunu kabul ediyoruz.

— Einstein 1907

Yani, dünya yüzeyinde hareketsiz durmanın boş uzayda motorları sayesinde ivmelenen bir uzay aracının içinde olmaktan hiçbir farkı yoktur. Bu prensipten yola çıkarak Einstein serbest düşmenin aslında eylemsiz bir hareket olduğu sonucuna vardı. Serbest düşme hareketi yapan cisimler gerçekte ivmelenmez. Eylemsiz referans sisteminde bulunan cisimler (ve ışık) sabit hızda ve düz bir doğrultuda hareket ettiklerinden Newton'un birinci hareket yasasına uyarlar. Benzer olarak eğimli uzay ve zaman içerisinde bulunan eylemsiz parçacıklar veya ışık atımlarının hareket doğrultusu olabildiğince düzdür. Bu tip hareket doğrusu kesel olarak adlandırılır. Yerçekimine maruz kalan cismin üzerinde bulunan hareketsiz durumdaki bir gözlemcinin zaman içindeki gözlemlerine göre bu keseller cisim boyunca eğilmeye başlar. İşte bu yüzden serbest düşme sırasında ivmeölçerler herhangi bir ivme tespit edemezler. Bunun aksine Newton mekaniğinde yerçekimi bir kuvvet olarak kabul edilir. Cisimleri büyük kütleli cisimlerin merkezine çeken bu kuvvettir. Dünya’nın yüzeyinde, yerçekimi kuvveti yüzeyden kaynaklanan mekanik bir direnç ile dengelenir. Bu yüzden Newton fiziğine göre, büyük kütleli bir cismin (dönüş hareketi yapmaya) üzerinde duran başka bir cisim eylemsiz hareket çerçevesi içerisinde bulunmaktadır. Bu değerlendirmeler doğal olarak Einstein’ın 1911’de kesin bir şekilde formüle ettiği eşdeğerlik ilkesini doğurur:

Gözlemci, tüm cisimler üzerine eylemsiz kütleleri ile orantılı şekilde etki eden bir kuvvet tespit ederse bu gözlemci ivmelenen bir eylemsiz hareket çerçevesindedir.

Einstein ayrıca K ve K’ olarak tanımlanan iki referans çerçevesinden söz etmiştir. K, düzgün bir kütleçekimsel alandır. K’ ise bir kütleçekimsel alana sahip olmamasına rağmen düzgün bir ivmeye sahiptir. Bu iki referans çerçevesindeki cisimler aynı kuvvetler etkisi altında kalır:

Eğer K ve K’ sistemleri fiziksel açıdan tam olarak aynı ise yani eğer K’yı kütleçekimsel alanlardan uzakta kabul edersek onu düzgün şekilde ivmelendiğini kabul edebiliriz. Bu fiziksel eşitlik varsayımı referans çerçevelerinin mutlak bir ivmeye sahip olduğundan tıpkı görelilik kuramının bize mutlak bir hız kavramından bahsetmemize engel olduğu gibi engel olur.

— Einstein 1911

Bu gözlem genel görelilikle sonuçlanan bir sürecin başlangıcını oluşturmuştur. Einstein görelilik kuramını oluştururken bunun genel bir prensip olarak kabul edilmesini önermiştir.

Kendimizi Newton yasaların kabul gördüğü gerçeklikte tamamen mekanik bir süreçle sınırlandırırsak K ve K’ sistemlerinin eşitliğinden emin olabiliriz. Ama bu bakış, K ve K’ nın tüm fiziksel süreçlerde eşit olduğu kabul edilmediği sürece herhangi bir derin öneme sahip olmayacaktır. ( Yani K ve K’ ya göre olan doğa kanunları uyum içinde değilse.) Bunun böyle olduğunu kabul ederek, eğer doğru ise, çok büyük bir buluşsal öneme sahip bir prensibe ulaşırız.

— Einstein 1911

Einstein özel görelilikle eşdeğerlik kuramını saatlerin kütleçekimsel alanda farklı çalıştığını ve ışık dalgalarının kütleçekimsel alanda büküldüğünü göstermek için birleştirmiştir. Bunu henüz eğimli uzay kavramını geliştirmeden önce geliştirmiştir. Eşdeğerlilik prensibi, Einstein’ın tarif ettiği şekilde, serbest düşüş ve eylemsiz hareketin aynı olduğu sonucuna varmıştır. Bu tip eşdeğerlik prensibi şu şekilde açıklanabilir. Penceresiz bir odada bulunan gözlemci Dünya yüzeyinde olduğunun ya da 1g’lik ivme ile ivmelenen bir uzay gemisinde olduğunun farkına varamaz. Bu durum tam olarak doğru değildir. Çünkü çok büyük kütleli cisimler derin uzayda ivmelenen uzay araçlarında görülmeyen gelgitsel kuvvetlere neden olur. Eşdeğerlik kuramının genel göreliliğin gelişmesinde rol oynamasına rağmen bu, genel göreliliğin bulunmasındaki temel prensip değildir. Daha çok kuramın geometrik doğasının sonucudur. Genel görelilikte, serbest düşüşteki cisimler uzay ve zamanın keselleri takip ederler ve kütleçekimsel kuvvet olarak algıladığımız şey ise uzay ve zamanın kesellerini takip edemememizin sonucudur çünkü maddenin mekanik direnci bizi bunu yapmaktan alıkoyar. Einstein genel göreliliği geliştirdiğinde bunu özel görelilikle uyumlu diğer kütleçekim kuramlarına karşı test etmek için bir yapı gerekiyordu. Bu tarafından genel görelilik testi programının bir parçası olarak geliştirildi. Einstein eşdeğerlilik prensibi ve güçlü eşdeğerlik prensibi denilen ve ikisinin de zayıf eşdeğerlik prensibini başlangıç noktası olarak kabul eden ve sadece kütleçekimsel deneylere uygulanabilir olup olmamaları açısından fark eden iki yeni prensip geliştirildi.

Modern kullanım

Eşdeğerlik prensibinin kullanımda olan üç formu zayıf, (Galileci) Einsteincı ve güçlü eşdeğerlik prensipleridir.

Zayıf eşdeğerliğik ilkesi

Zayıf eşdeğerlik ilkesi, serbest düşüşün evrenselliği ya da Galileci eşdeğerlik prensibi olarak da bilinir. Güçlü EP kütleçekimsel bağlanım enerjisine sahip astronomik cisimleri içerir. Zayıf EP, kütleçekimsel olmayan kuvvetler ile bağlanmış düşen cisimleri dikkate alır. İki türde de:

• Kütleçekimsel alandaki noktasal kütlenin yörüngesi sadece kütlenin ilk hızına ve pozisyonuna bağlıdır. Cismin yapısından bağımsızdır.
• Belirli bir kütleçekimsel alanda benzer noktalarda bulunan tüm test parçacıklar aynı ivmeye maruz kalır. Bu parçacıkların özelliklerinden bağımsızdır.
• Eğimli uzayda hareket eden gözlemcinin hissedeceği etkiler düz uzayda ivmelenen gözlemcinin gözleyeceği etkilerden hiçbir istisna olmadan ayır edilemezdir.
• Kütle ve ağırlık bölgesel olarak tüm cisimler için aynı orana sahiptir.

Bölgesellik, dairesel ıraksak kütleçekimi alanından kaynaklanan sonlu boyuttaki fiziksel cisimlere etki eden gelgitsel kuvvetleri iptal eder. Düşme eşdeğerlik prensibi Galileo'nun Newton'un ve Einstein'in kavramlaştırmalarını kapsar. Eşdeğerlik prensibi dönüş hareketi yapan kütleçekimsel cisim yüzünden oluşan ölçülebilir etkileri ya da ışığın bükülmesi ve saatlerin farklı çalışmasına dair bölgesel olmayan gözlemciler tarafından yapılan ölçümleri reddetmez.

Aktif, pasif ve eylemsiz kütleler

Aktif ve pasif kütle tanımından yola çıkarak, ${\displaystyle M_{1}}$ kütlesi üzerindeki, ${\displaystyle M_{0}}$ ‘ın kütleçekimsel alanı nedeniyle oluşan kuvvet:

${\displaystyle F_{1}={\frac {M_{0}^{\mathrm {aktif} }M_{1}^{\mathrm {pasif} }}{r^{2}}}}$

Ayı şekilde ikinci bir rastgele seçilen 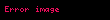${\displaystyle M_{2}}$ kütlesi üzerindeki, ${\displaystyle M_{0}}$ ‘ın kütleçekimsel alanı nedeniyle oluşan kuvvet:

${\displaystyle F_{2}={\frac {M_{0}^{\mathrm {aktif} }M_{2}^{\mathrm {pasif} }}{r^{2}}}}$

Eylemsiz kütle tanımından yola çıkılarak:

${\displaystyle F=m^{\mathrm {eylm} }a}$

Eğer ${\displaystyle m_{1}}$ ve ${\displaystyle m_{2}}$, ${\displaystyle m_{0}}$ ‘dan eşit ${\displaystyle r}$ uzaklığındaysalar. Zayıf eşdeğerlik ilkesi nedeniyle aynı oranda düşerler. Yani ivmeleri aynı olur.

${\displaystyle a_{1}={\frac {F_{1}}{m_{1}^{\mathrm {eylm} }}}=a_{2}={\frac {F_{2}}{m_{2}^{\mathrm {eylm} }}}}$

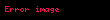
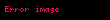
Bundan dolayı:

${\displaystyle {\frac {M_{0}^{\mathrm {aktif} }M_{1}^{\mathrm {pasif} }}{r^{2}m_{1}^{\mathrm {eylm} }}}={\frac {M_{0}^{\mathrm {aktif} }M_{2}^{\mathrm {pasif} }}{r^{2}m_{2}^{\mathrm {eylm} }}}}$

Ve:

${\displaystyle {\frac {M_{1}^{\mathrm {pasif} }}{m_{1}^{\mathrm {eylm} }}}={\frac {M_{2}^{\mathrm {pasif} }}{m_{2}^{\mathrm {eylm} }}}}$

Diğer bir deyişle pasif kütleçekimsel kuvvet tüm cisimler için aktif kütleçekimsel kuvvet ile oranlı olmalıdır. Newton’un üçüncü hareket yasası göz önüne alındığında:

${\displaystyle F_{1}={\frac {M_{0}^{\mathrm {aktif} }M_{1}^{\mathrm {pasif} }}{r^{2}}}}$

${\displaystyle F_{0}={\frac {M_{1}^{\mathrm {aktif} }M_{0}^{\mathrm {pasif} }}{r^{2}}}}$ ifadesine eşit ve karşıt olmalıdır.

Buradan

${\displaystyle {\frac {M_{0}^{\mathrm {aktif} }}{M_{0}^{\mathrm {pasif} }}}={\frac {M_{1}^{\mathrm {aktif} }}{M_{1}^{\mathrm {pasif} }}}}$

Elde edilir.

Diğer bir deyişle pasif kütleçekimsel kuvvet tüm cisimler için aktif kütleçekimsel kuvvet ile oranlı olmalıdır. Birimsiz Eötvös değişkeni ${\displaystyle \eta (A,B)}$ kütleçekimsel ve eylemsiz kütlelerin iki A ve B test kütleleri grubunun ortalamalarına bölümünün oranları farkıdır.

${\displaystyle \eta (A,B)=2{\frac {\left({\frac {m_{k}}{m_{e}}}\right)_{A}-\left({\frac {m_{k}}{m_{e}}}\right)_{B}}{\left({\frac {m_{k}}{m_{e}}}\right)_{A}+\left({\frac {m_{k}}{m_{e}}}\right)_{B}}}}$

Zayıf eşdeğerlik ilkesi testleri

Zayıf eşdeğerlik ilkesi testleri eylemsiz ve kütleçekimsel kütlelerin eşdeğerliliğini doğrulayan testlerdir. Yapılabilecek en bariz test karşılaştırılan iki cismi gibi bir vakumun içinde serbest bırakmaktır.

Araştırmacı	Yıl	Yöntem	Sonuç
John Philoponus	6. yüzyıl	İki farklı kütledeki topların düşüşünün etkisini tanımladı	Belirlenebilir bir fark yoktur
	~1586	Farklı kütledeki iki kurşun topu Delft kilise kulesinden serbest bıraktı	Belirlenebilir bir fark yoktur
Galileo Galilei	~1610	Eğimli düzlemden toplar yuvarladı	Belirlenebilir bir fark yoktur
Isaac Newton	~1680	Aynı uzunlukta ancak farklı kütledeki sarkaçların periyodunu ölçtü	Ölçülebilir bir fark yoktur
Friedrich Wilhelm Bessel	1832	Aynı uzunlukta ancak farklı kütledeki sarkaçların periyodunu ölçtü	Ölçülebilir bir fark yoktur
Loránd Eötvös	1908	Aynı kütleye sahip, yerçekimi ve Dünya’nın dönüşü etkisindeki iki cisim için ipler üzerindeki burulmayı ölçtü	Fark 10^9 da 1’den daha az
, ve	1964	Burulma terazisi deneyi, alüminyum ve altın test kütlelerinin düşürülmesi	${\displaystyle |\eta (\mathrm {Al} ,\mathrm {Au} )|=(1.3\pm 1.0)\times 10^{-11}}$
David Scott	1971	Ay üzerinde şahin tüyü ve çekici aynı anda düşürdü	Belirlenebilir bir fark yoktur.
ve	1971	Burulma Terazisi, alüminyum ve platinyum test kütleleri, güneşe doğru olan ivmenin ölçümü	Fark 10^12 da 1’den daha azdır
Eöt-Wash Grubu	1987–	Burulma Terazisi, farklı kütlelerin Dünya’ya doğru olan ivmelerinin ölçülmesi, güneş ve galaktik merkez, birçok farklı türde kütle kullanmak	${\displaystyle \eta ({\text{Earth}},{\text{Be-Ti}})=(0.3\pm 1.8)\times 10^{-13}}$

Yıl	Araştırmacı	Hassaslık	Yöntem
500?	Philoponus	"küçük"	Düşürme Kulesi
1585	Stevin	5×10^-2	Düşürme Kulesi
1590?	Galileo	2×10^-2	Sarkaç, Düşürme Kulesi
1686	Newton	10^-3	Sarkaç
1832	Bessel	2×10^-5	Sarkaç
1910	Southerns	5×10^-6	Sarkaç
1918	Zeeman	3×10^-8	Burulma Terazisi
1922	Eötvös	5×10^-9	Burulma Terazisi
1923	Potter	3×10^-6	Sarkaç
1935	Renner	2×10^-9	Burulma Terazisi
1964	Dicke, Roll, Krotkov	3x10^-11	Burulma Terazisi
1972	Braginsky, Panov	10^-12	Burulma Terazisi
1976	Shapiro	10^-12	Lazer Ay Deneyi
1981	Keiser, Faller	4×10^-11	Sıvı Desteği
1987	Niebauer	10^-10	Düşürme Kulesi
1989	Stubbs,	10^-11	Burulma Terazisi
1990	Adelberger, Eric G	10^-12	Burulma Terazisi
1999	Baessler	5x10^-14	Burulma Terasizi

Bu konu hakkındaki deneyler hala Washington Üniversitesi'nde devam etmektedir

Einstein Eşdeğerlik İlkesi

Einstein, eşdeğerlik ilkesi zayıf eşdeğerlik ilkesinin işlediğini ve : “Bir serbest düşüş laboratuvarında herhangi bir bölgesel kütleçekimsel olmayan deneyin sonucu laboratuvarın ve onun bulunduğu yerin uzay-zamandaki hızından bağımsızdır.” İfadesini öne sürer. Burada “bölgesel” çok özel bir anlama sahiptir. Sadece deneyin laboratuvarın dışından görülmemesi gerektiği değil, aynı zamanda kütleçekimsel alandaki değişimlerle karşılaştırıldığında küçük olmalıdır. Böylece tüm laboratuvar serbest düşüşte olur. Bu ayrıca dış alanlarla etkileşimin yokluğuna da işaret eder. Görelilik ilkesi, bölgesel deneylerin kullanılan aletlerin hızından bağımsız olması gerektiğini işaret eder, bu ilkenin en önemli sonucu fiziksel sabitlerin uzay ve zamandaki hiçbir konuma bağlı olmaması gerektiğini savunan Copernikçi fikirdir. Birçok fizikçi zayıf eşdeğerlilik ilkesini sağlayan herhangi bir Lorentz sabit kuramının Einstein eşdeğerlilik prensibini de sağlayacağına inanır. Schiff’in tahmini zayıf eşdeğerli ilkesinin Einstein eşdeğerlik ilkesini sağladığını öne sürer ancak bu henüz kanıtlanmamıştır. Yine de iki önemli ilke birçok farklı deney ile test edilmiştir. Einstein eşdeğerlik ilkesi kesinliğe sahip olmadığı konusunda eleştirilmektedir çünkü kütleçekimsel deneyleri kütleçekimsel olmayanlardan ayıracak evrensel bir yöntem yoktur.

Einstein Eşdeğerlik İlkesi deneyleri

Einstein eşdeğerlik prensibi boyutsuz sabitlerde ve kütle oranlarında bir değişim arayarak test edilebilir.

Sabit	Yıl	Yöntem	Limit on fractional change
İnce Yapı Sabitleri	1976	Oklo	10^−7
Zayıf Etkileşim Sabiti	1976	Oklo	10^−2
elektron-proton kütle oranı	2002	yıldızsı gök cisimleri	10^−4
proton dönel mıknatıssal oran	1976	astrofiziksel	10^−1

Güçlü eşdeğerlik ilkesi

Güçlü eşdeğerlik ilkesi kütleçekim kanunlarının hız ve konumdan bağımsız olduğunu öne sürer:

Küçük bir test cisminin kütleçekimsel hareketi cismin bünyesine değil sadece cismin uzay-zamandaki ilk konumuna ve hızına bağlıdır.

Herhangi bir serbest düşme laboratuvarında yapılan bölgesel bir deneyin sonucu laboratuvarın uzay-zamandaki hızı ve konumundan bağımsızdır.

İlk kısım zayıf eşdeğerlik prensibinin bir başka çeşididir ve kendilerine kütleçekimsel kuvvet uygulayan yıldız, gezegen ve karadelik gibi cisimler için geçerlidir. İkinci kısım ise kütleçekimsel deneylere ve kendilerine kütleçekimi uygulayan cisimlere izin veren bir Einstein eşdeğerlik ilkesidir. Bu kendilerine kütleçekimsel kuvvet uygulayan ve önemli miktarda içsel kütleçekimsel etkileşime sahip cisimlere izin veren tek eşdeğerlik prensibidir. Kütleçekim sabitinin evrenin her yerinde aynı olmasını gerektirir. Bu Einstein eşdeğerlik prensibinden daha sınırlayıcıdır. Güçlü eşdeğerlik ilkesi kütleçekiminin doğası gereği geometrik olduğunu ve birlikte olduğu başka fazladan alan olmadığını öne sürer. Eğer bir gözlemci uzayın bir kısmını düz olarak ölçerse güçlü eşdeğerlik prensibi bu ölçülen alanın evrendeki herhangi bir düz alanla tamamen aynı olduğunu iddia eder. Einstein’ın genel görelilik kuramı güçlü eşdeğerlik ilkesini sağlayan tek kuram olarak görülür. Diğer kuramlar ise sadece Einstein eşdeğerlik prensibini sağlar.

Güçlü eşdeğerlik ilkesi testleri

Güçlü eşdeğerlik ilkesi Newton’un kütleçekim sabiti G evren boyunca ya da eşdeğer şekilde temel parçacıkların kütlelerindeki değişim aranarak test edilebilir. Yapılan araştırmalar G’nin %10’dan fazla değişmediğini ortaya koymuştur. Bu deneyler genellikle ters kare kuralının başarısız olduğu noktaları arar. Kısa mesafelerde en başarılı testler Eöt-Wash grubu tarafından yapılmıştır. Diğer testler uzak mesafelerdeki radyo kaynaklarının güneş tarafından saptırılmasının araştırmasını içerir. Bütün bu testler ve diğer alternatif kütleçekimi kuramlarına büyük sınırlamalar koymuştur. 2014’te astronomlar bir milisaniye pulsarı PSR J0337+1715’i ve iki adet beyaz cüce içeren üçlü bir yıldız sistemi keşfettiler. Bu sistem onlara güçlü eşdeğerlik ilkesini güçlü kütleçekimsel alanda test etme imkânı sağlayacaktır.

Eşdeğerlik ilkesinin karşılaştığı zorluklar

Eşdeğerlik ilkesinin karşılaştığı zorluklardan biri . Kendiliğinden oluşan kozmoloji kuramı Brans-Dicke kuramının değiştirilmiş halidir. çok az destekçisi olmasına rağmen eşdeğerlik ilkesinin önüne koyulan ciddi engellerdendir. Ağustos 2010’da Fizik Okulundan, 'nden, 'nden, 'nden, ve Cambridge'den bir grup araştırmacı “İnce Yapı Sabitinin Mekânsal Değişimi İçin Kanıt” başlığı altında bir makale yayımlanışlardır. Bu makalenin muhtemel sonucu “ Nitelik bakımından sonuçlar Einstein Eşdeğerlik ilkesinin ihlalini öne sürmektedir ve bu sonuçlar bizim bölgesel Hubble hacmimizin çok ufak bir parçasını oluşturduğu çok büyük veya sonsuz evren anlamına gelebilir.” dir.

Eşdeğerlik ilkesinin açıklamaları

Hollandalı fizikçi ve sicim kuramcısı holografik evren varsayımına dayanarak eşdeğerlik ilkesinin bağımsız bir mantıksal türetimini üretmiştir. Bu durumda kütleçekimi, normalde olduğu gibi temel bir kuvvet olmak yerine entropi sonucu ortaya çıkan bir özellik olmaktadır.

Deneyler

• “…Almanya’daki fizikçiler atomik seviyede bu zamana kadarki en hassas eşdeğerlik ilkesi deneyini gerçekleştirmek için bir atomik girişimölçer kullandılar…”