Bu madde, uygun değildir. (Nisan 2011) |
Fizikte Gauss'un akı teoremi olarak da bilinen Gauss yasası, elektrik yükünün ortaya çıkan elektrik alanına dağılımına ilişkilendiren matematiksel bir yasadır. Söz konusu yüzey küresel yüzey gibi bir hacmi çevreleyen kapalı bir yüzey olabilir.
Yasa ilk olarak J. Louis Lagrange tarafından 1773 yılında düşünüldü. Ardından C. Friedrich Gauss tarafından 1813'te her ikisi de elipsoidlerin çekiciliği bağlamında formüle edildi. Gauss yasası klasik elektrodinamiğin temelini oluşturan Maxwell'in 4 denkleminden birisidir. Gauss yasası Coulomb yasasını türetmek için kullanılabilir ve bunun tersi de geçerlidir.
Başlıca fizik ve matematiksel çözümleme alanlarında kullanılır.
Nitel Açıklama
Kelimelerle Gauss yasası, herhangi bir kapalı yüzeyden geçen net elektrik akısı, yüzeyin sarmaladığı net yükün 
Gauss yasası Gauss'un manyetizma yasası ve Gauss'un yerçekimi yasası gibi fiziğin diğer alanlarındaki bir dizi yasayla yakın bir matematiksel benzerliğe sahiptir. Aslında herhangi bir ters kare yasası Gauss yasasına benzer bir şekilde formüle edilebilir. Örneğin Gauss yasasının kendisi ters kare yasası olan Coulomb yasasıyla eşdeğerdir. Aynı şekilde Newton'un kütleçekim yasası bir ters kare yasasıdır ve Gauss'un yerçekimi yasası ile eşdeğer bir niteliğe sahiptir.
Yasa tümlev formda ve diferansiyel formda Vektör Analizi yardımı ile matematiksel olarak ifade edilebilir. Gauss yasası, bir başka adı Gauss teoremi olarak da adlandırılan diverjans teoremi üzerine oturtturulmuştur. Bu formların (tümlev ve diferansiyel) her biri sırayla iki şekilde ifade edilebilir:
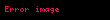

Elektrik Alanını İçeren Denklem
Gauss yasası, elektrik alanı ve elektrik yer değiştirme alanı kullanılarak ifade edilebilir. Bu bölüm elektrik alanıyla bazı formları gösterir, elektrik yer değiştirme alanı ile gösterilen formlar aşağıdadır.
Tümlev Form
Gauss yasası kısaca şöyle ifade edilebilir:

Burada 




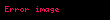


Burada 


Akı, elektrik alanının tümlevi olarak tanımlandığından, Gauss yasasının bu ifadesine tümlev ya da integral form denir.
Eğer elektrik alanı her yerde biliniyorsa, Gauss yasası elektrik yükünün dağılımını bulmayı mümkün kılar. Herhangi bir bölgedeki yük, akıyı bulmak için elektrik alanı entegre edilerek çıkarılabilir. Tersi durumda (elektrik yükü dağılımı bilindiğinde ve elektrik alanı hesaplanması gerektiğinde) işler zorlaşacaktır. Belirli bir yüzeyden geçen toplam akı, elektrik alanı hakkında çok az bilgi verir ve rastgele karmaşık desenlerde yüzeye girip çıkabilir.
Bir istisna, problemde elektrik alanın yüzeyden düzgün bir şekilde geçmesini zorunlu kılan bir simetri bulunmasıdır. Daha sonra toplam akı biliniyorsa alanın kendisi her noktada çıkarılabilir. Gauss yasasına uygun olan yaygın simetri örnekleri, silindirik simetri, küresel simetri ve düzlemsel simetri verilebilir. Detaylı bilgi için Gauss yüzeylerine bakabilirsiniz..
Diferansiyel Form
Diverjans teoremi ile yasa diferansiyel formda da yazılabilir:

burada 
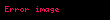

Diferansiyel ve İntegral formların eşitliği
Ana madde :Diverjans teoremi
Matematiksel olarak integral ve diferansiyel form diverjans teoremi vasıtasıyla birbirine eşitlenebilir.
İspat:
Gauss yasasının integral formu:



Diverjans teoremi ile bu denklem şu şekilde yazılabilir:

(

Yük ve yük yoğunluğu arasındaki ilişkiye göre bu denklem eşdeğerdir:
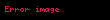
Bu denklemin her olası 
 | Fizik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Nisan 2011 Fizikte Gauss un aki teoremi olarak da bilinen Gauss yasasi elektrik yukunun ortaya cikan elektrik alanina dagilimina iliskilendiren matematiksel bir yasadir Soz konusu yuzey kuresel yuzey gibi bir hacmi cevreleyen kapali bir yuzey olabilir Yasa ilk olarak J Louis Lagrange tarafindan 1773 yilinda dusunuldu Ardindan C Friedrich Gauss tarafindan 1813 te her ikisi de elipsoidlerin cekiciligi baglaminda formule edildi Gauss yasasi klasik elektrodinamigin temelini olusturan Maxwell in 4 denkleminden birisidir Gauss yasasi Coulomb yasasini turetmek icin kullanilabilir ve bunun tersi de gecerlidir Baslica fizik ve matematiksel cozumleme alanlarinda kullanilir Nitel AciklamaKelimelerle Gauss yasasi herhangi bir kapali yuzeyden gecen net elektrik akisi yuzeyin sarmaladigi net yukun e0 displaystyle varepsilon 0 a bolumudur Gauss kanununun uygulanabilmesi icin yuk etrafinda uygun kapali yuzeyler secilmelidir Gauss yasasi Gauss un manyetizma yasasi ve Gauss un yercekimi yasasi gibi fizigin diger alanlarindaki bir dizi yasayla yakin bir matematiksel benzerlige sahiptir Aslinda herhangi bir ters kare yasasi Gauss yasasina benzer bir sekilde formule edilebilir Ornegin Gauss yasasinin kendisi ters kare yasasi olan Coulomb yasasiyla esdegerdir Ayni sekilde Newton un kutlecekim yasasi bir ters kare yasasidir ve Gauss un yercekimi yasasi ile esdeger bir nitelige sahiptir Yasa tumlev formda ve diferansiyel formda Vektor Analizi yardimi ile matematiksel olarak ifade edilebilir Gauss yasasi bir baska adi Gauss teoremi olarak da adlandirilan diverjans teoremi uzerine oturtturulmustur Bu formlarin tumlev ve diferansiyel her biri sirayla iki sekilde ifade edilebilir E displaystyle mathrm E elektrik alani ile toplam elektrik yuku arasindaki iliski acisindan veya elektrik yer degistirme alani D displaystyle D ve serbest elektrik yuku acisindan ifade edilebilir Elektrik Alanini Iceren DenklemGauss yasasi elektrik alani ve elektrik yer degistirme alani kullanilarak ifade edilebilir Bu bolum elektrik alaniyla bazi formlari gosterir elektrik yer degistirme alani ile gosterilen formlar asagidadir Tumlev Form Gauss yasasi kisaca soyle ifade edilebilir FE Qϵ0 displaystyle Phi E Q over epsilon 0 Burada FE displaystyle Phi E herhangi bir V displaystyle V hacmini cevreleyen kapali bir S displaystyle S yuzeyinden gecen toplam elektrik akisidir Q displaystyle Q V displaystyle V hacmindeki toplam yuktur ve ϵ0 displaystyle epsilon 0 elektrik sabitidir Elektrik akisi FE displaystyle Phi E elektrik alaninin yuzey integrali olarak tanimlanir FE AE dA displaystyle Phi E oint A mathbf E cdot mathrm d mathbf A Burada E displaystyle E elektrik alanini dA displaystyle dA yuzey alaninin sonsuz kucuk elemanini temsil eden bir vektoru ve displaystyle cdot iki vektorun ic carpimini temsil eder Aki elektrik alaninin tumlevi olarak tanimlandigindan Gauss yasasinin bu ifadesine tumlev ya da integral form denir Eger elektrik alani her yerde biliniyorsa Gauss yasasi elektrik yukunun dagilimini bulmayi mumkun kilar Herhangi bir bolgedeki yuk akiyi bulmak icin elektrik alani entegre edilerek cikarilabilir Tersi durumda elektrik yuku dagilimi bilindiginde ve elektrik alani hesaplanmasi gerektiginde isler zorlasacaktir Belirli bir yuzeyden gecen toplam aki elektrik alani hakkinda cok az bilgi verir ve rastgele karmasik desenlerde yuzeye girip cikabilir Bir istisna problemde elektrik alanin yuzeyden duzgun bir sekilde gecmesini zorunlu kilan bir simetri bulunmasidir Daha sonra toplam aki biliniyorsa alanin kendisi her noktada cikarilabilir Gauss yasasina uygun olan yaygin simetri ornekleri silindirik simetri kuresel simetri ve duzlemsel simetri verilebilir Detayli bilgi icin Gauss yuzeylerine bakabilirsiniz Diferansiyel Form Diverjans teoremi ile yasa diferansiyel formda da yazilabilir E re0 displaystyle mathbf nabla cdot mathbf E frac rho varepsilon 0 burada E displaystyle mathbf nabla cdot mathbf E elektrik alaninin diverjansi ϵ0 displaystyle epsilon 0 elektrik sabiti ve r displaystyle rho birim hacimde ki yuk miktari ya da yuk yogunlugudur Diferansiyel ve Integral formlarin esitligi Ana madde Diverjans teoremi Matematiksel olarak integral ve diferansiyel form diverjans teoremi vasitasiyla birbirine esitlenebilir Ispat Gauss yasasinin integral formu AE dA Qe0 displaystyle oint A mathbf E cdot mathrm d mathbf A frac Q varepsilon 0 Q displaystyle Q yukunu iceren herhangi bir kapali A displaystyle A yuzeyi icin Diverjans teoremi ile bu denklem su sekilde yazilabilir V E dV Qe0 displaystyle iiint limits V nabla cdot mathbf E mathrm d V Q over varepsilon 0 Q displaystyle Q yukunu iceren herhangi bir V displaystyle V hacmi icin Yuk ve yuk yogunlugu arasindaki iliskiye gore bu denklem esdegerdir Vre0 dV V E dV displaystyle iiint limits V frac rho varepsilon 0 mathrm d V iiint limits V nabla cdot mathbf E mathrm d V Bu denklemin her olasi V displaystyle V hacmi icin ayni anda dogru olabilmesi icin integrallerin her yerde esit olmasi gerekir Bu nedenle denklem suna esdegerdir E re0 displaystyle mathbf nabla cdot mathbf E frac rho varepsilon 0 Fizik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State