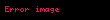Matematikte Hankel dönüşümü, diğer adıyla Fourier–Bessel dönüşümü, herhangi bir f(r) fonksiyonunu sonsuz sayıda birinci tip Bessel fonksiyonlarının Jν(kr) oranlı toplamı olarak gösterir. Bu dönüşümde ortogonal temeli oluşturan Bessel fonksiyonlarının hepsi aynı ν mertebesindedir. Bu ilk kez matematikçi Hermann Hankel tarafından tasvir edilmiştir. Formülü ve ters dönüşümü sırasıyla şu şekilde verilebilir:
Fourier dönüşümü ile Fourier serisi arasındaki ilişkinin benzeri Hankel dönüşümü ile arasında da vardır. Hankel dönüşümü iki boyutlu Fourier dönüşümünün dairesel olarak simetrik bir versiyonu olarak düşünülebilir; bu nedenle bu dönüşüm fizik ve mühendislikte silindirik veya dairesel simetrinin bulunduğu birçok problemde kullanılır.
Dönüşüm tablosu
Bazı yaygın Hankel dönüşümleri şu şekilde gösterilebilir:
 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 | |
 |  |
 |  |
 |  |
 |  |
|---|---|
 |  |
 | 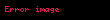 |
 |  |
 | Eliptik integraller ile gösterilebilir. |
 | 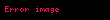 |
Ayrıca bakınız
Kaynakça
- ^ Gaskill, Jack D. (1978). Linear Systems, Fourier Transforms, and Optics (İngilizce). New York: John Wiley & Sons. ISBN .
- ^ Weisstein, Eric W. "Hankel Transform" (İngilizce). wolfram.com. 5 Ağustos 2002 tarihinde kaynağından . Erişim tarihi: 15 Haziran 2020.
- ^ Arfken, G. (1985). Mathematical methods for physicists (İngilizce) (3 bas.). Orlando, FL: Academic Press. ISBN .
- ^ Papoulis, Athanasios (1981). Systems and Transforms with Applications to Optics (İngilizce). Florida: Krieger Publishing Company. ss. 140-175. ISBN .
- ^ Kausel, E.; Irfan Baig, M. M. (2012). "Laplace transform of products of Bessel functions: A visitation of earlier formulas" (PDF). Quarterly of Applied Mathematics. 70: 77-97. doi:10.1090/s0033-569x-2011-01239-2. hdl:1721.1/78923.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Hankel donusumu diger adiyla Fourier Bessel donusumu herhangi bir f r fonksiyonunu sonsuz sayida birinci tip Bessel fonksiyonlarinin Jn kr oranli toplami olarak gosterir Bu donusumde ortogonal temeli olusturan Bessel fonksiyonlarinin hepsi ayni n mertebesindedir Bu ilk kez matematikci Hermann Hankel tarafindan tasvir edilmistir Formulu ve ters donusumu sirasiyla su sekilde verilebilir Fn k 0 f r Jn kr rdr displaystyle F nu k int 0 infty f r J nu kr r mathrm d r f r 0 Fn k Jn kr kdk displaystyle f r int 0 infty F nu k J nu kr k mathrm d k Fourier donusumu ile Fourier serisi arasindaki iliskinin benzeri Hankel donusumu ile arasinda da vardir Hankel donusumu iki boyutlu Fourier donusumunun dairesel olarak simetrik bir versiyonu olarak dusunulebilir bu nedenle bu donusum fizik ve muhendislikte silindirik veya dairesel simetrinin bulundugu bircok problemde kullanilir Donusum tablosuBazi yaygin Hankel donusumleri su sekilde gosterilebilir f r displaystyle f r F0 k displaystyle F 0 k 1 displaystyle 1 d k k displaystyle frac delta k k 1r displaystyle frac 1 r 1k displaystyle frac 1 k r displaystyle r 1k3 displaystyle frac 1 k 3 r3 displaystyle r 3 9k5 displaystyle frac 9 k 5 rm displaystyle r m 2m 1G m2 1 km 2G m2 2 lt ℜ m lt 12 displaystyle frac 2 m 1 Gamma left tfrac m 2 1 right k m 2 Gamma left tfrac m 2 right quad 2 lt Re m lt tfrac 1 2 1r2 z2 displaystyle frac 1 sqrt r 2 z 2 e k z k displaystyle frac e k z k 1z2 r2 displaystyle frac 1 z 2 r 2 K0 kz z C displaystyle K 0 kz quad z in mathbf C eiarr displaystyle frac e iar r ia2 k2 a gt 0 k lt a displaystyle frac i sqrt a 2 k 2 quad a gt 0 k lt a 1k2 a2 a gt 0 k gt a displaystyle frac 1 sqrt k 2 a 2 quad a gt 0 k gt a e 12a2r2 displaystyle e frac 1 2 a 2 r 2 1a2e k22a2 displaystyle frac 1 a 2 e tfrac k 2 2a 2 1rJ0 lr e sr displaystyle frac 1 r J 0 lr e sr 2p k l 2 s2K 4kl k l 2 s2 displaystyle frac 2 pi sqrt k l 2 s 2 K bigg sqrt frac 4kl k l 2 s 2 bigg r2f r displaystyle r 2 f r d2F0dk2 1kdF0dk displaystyle frac mathrm d 2 F 0 mathrm d k 2 frac 1 k frac mathrm d F 0 mathrm d k f r displaystyle f r Fn k displaystyle F nu k rs displaystyle r s 2s 1ks 2G 12 2 n s G 12 n s displaystyle frac 2 s 1 k s 2 frac Gamma left tfrac 1 2 2 nu s right Gamma tfrac 1 2 nu s rn 2sG s r2h displaystyle r nu 2s Gamma s r 2 h 12 k2 2s n 2g 1 s n k24h displaystyle tfrac 1 2 left tfrac k 2 right 2s nu 2 gamma left 1 s nu tfrac k 2 4h right e r2rnU a b r2 displaystyle e r 2 r nu U a b r 2 G 2 n b 2G 2 n b a k2 ne k241F1 a 2 a b n k24 displaystyle frac Gamma 2 nu b 2 Gamma 2 nu b a left tfrac k 2 right nu e frac k 2 4 1 F 1 left a 2 a b nu tfrac k 2 4 right rnJm lr e sr displaystyle r n J mu lr e sr Eliptik integraller ile gosterilebilir r2f r displaystyle r 2 f r d2Fndk2 1kdFndk n2k2Fn displaystyle frac mathrm d 2 F nu mathrm d k 2 frac 1 k frac mathrm d F nu mathrm d k frac nu 2 k 2 F nu Ayrica bakinizLaplace donusumuKaynakca Gaskill Jack D 1978 Linear Systems Fourier Transforms and Optics Ingilizce New York John Wiley amp Sons ISBN 978 0 471 29288 3 Weisstein Eric W Hankel Transform Ingilizce wolfram com 5 Agustos 2002 tarihinde kaynagindan Erisim tarihi 15 Haziran 2020 Arfken G 1985 Mathematical methods for physicists Ingilizce 3 bas Orlando FL Academic Press ISBN 9780120598205 Papoulis Athanasios 1981 Systems and Transforms with Applications to Optics Ingilizce Florida Krieger Publishing Company ss 140 175 ISBN 978 0898743586 Kausel E Irfan Baig M M 2012 Laplace transform of products of Bessel functions A visitation of earlier formulas PDF Quarterly of Applied Mathematics 70 77 97 doi 10 1090 s0033 569x 2011 01239 2 hdl 1721 1 78923
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State