Matematikte, Laplace dönüşümü, zaman tanım kümesinde tanımlı bir fonksiyonu, frekans tanım kümesinde tanımlı bir başka fonksiyona dönüştürmek amacıyla kullanılır.
Laplace dönüşümü ile diferansiyel denklemler çözmesi daha kolay polinomlara dönüştüğü için, zamandan bağımsız doğrusal sistemlerin modellenmesinde ve diferansiyel denklemlerin çözülmesinde, başlangıç değer teoremi, son değer teoremi ve sınır değer problemi gibi çeşitli problemlerde, olasılık teorisinde ve ilgili fonksiyonun frekans karakteristiğini net bir şekilde göstermesinden dolayı sinyal işlemede de kullanılır.
İsim babası, bu yöntemi geliştiren Pierre-Simon Laplace'tır.
Verilen bir f(t) fonksiyonunun (tüm t ≥ 0 reel sayıları için tanımlı) Laplace dönüşümü F(s) matematiksel olarak şöyle gösterilir:
Özellikler ve teoremler
Laplace dönüşümü doğrusal dinamik sistemlerin incelenmesini kolaylaştıran bazı özelliklere sahiptir. En önemli özelliği, türevi 

Verilen f(t) ve g(t) fonksiyonları ve bunların Laplace dönüşümleri F(s) ve G(s) için
aşağıdaki tablo tek yanlı Laplace dönüşümünün özelliklerinin bir listesidir:
| Zaman tanım | Frekans tanım | Yorum | |
|---|---|---|---|
| Doğrusallık |  |  | İntegralin temel kurallarıyla kanıtlanabilir. |
| Frekans Türevlemesi |  |  | |
| Genel Frekans Türevlemesi |  |  | Genel olarak |
| Türevleme |  |  | İntegralin açık hali yazılıp, bu integralde kısmi integrasyon yöntemi kullanılarak bulunabilir. |
| İkinci Türevleme |  |  |  fonksiyonuna Türevleme özelliği uygulanır. fonksiyonuna Türevleme özelliği uygulanır. |
| Genel Türevleme |  |  | İkinci türevle ilgili sonuçtan tümevarımla bulunmuştur. |
| Frekans Entegrasyonu |  |  | |
| Entegrasyon |  |  | 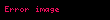 . . |
| Ölçekleme |  |  | |
| Frekans öteleme |  |  | |
| Zaman öteleme |  |  | 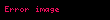 . . |
| (Konvülsiyon) |  |  | |
| Periyodik Fonksiyon |  |  |  bir periyodik fonksiyon periyot bir periyodik fonksiyon periyot  şöyle ki şöyle ki  |
- Başlangıç değer teoremi:
- Son değer teoremi:
, Paydanın kökleri sol taraf düzlemindedir.
- son değer teoremi bir fonksiyonun uzun dönem davranışını basit kesirlere ayırma veya diğer zorlu cebir işlemler uygulamaksızın verdiği için yararlıdır. Eğer bir fonksiyonun kökleri sağ taraf düzlemindeyse (örn.
or
) bu formülün davranışı tanımsızdır.
Ayrıca bakınız
Dış bağlantılar
- http://wims.unice.fr/wims/wims.cgi 10 Şubat 2008 tarihinde Wayback Machine sitesinde . (Verilen bir fonksiyonun hem Laplace ve Fourier dönüşümlerini, hem de ters dönüşümlerini hesaplayan bir site)
Kaynakça
- ^ Korn & Korn 1967, ss. 226–227
Bibliyografya
- Korn, G. A.; Korn, T. M. (1967), Mathematical Handbook for Scientists and Engineers, 2nd, McGraw-Hill Companies, ISBN
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Laplace donusumu zaman tanim kumesinde tanimli bir fonksiyonu frekans tanim kumesinde tanimli bir baska fonksiyona donusturmek amaciyla kullanilir Laplace donusumu ile diferansiyel denklemler cozmesi daha kolay polinomlara donustugu icin zamandan bagimsiz dogrusal sistemlerin modellenmesinde ve diferansiyel denklemlerin cozulmesinde baslangic deger teoremi son deger teoremi ve sinir deger problemi gibi cesitli problemlerde olasilik teorisinde ve ilgili fonksiyonun frekans karakteristigini net bir sekilde gostermesinden dolayi sinyal islemede de kullanilir Isim babasi bu yontemi gelistiren Pierre Simon Laplace tir Verilen bir f t fonksiyonunun tum t 0 reel sayilari icin tanimli Laplace donusumu F s matematiksel olarak soyle gosterilir F s L f t 0 e stf t dt displaystyle F s mathcal L left f t right int 0 infty e st f t dt Ozellikler ve teoremlerLaplace donusumu dogrusal dinamik sistemlerin incelenmesini kolaylastiran bazi ozelliklere sahiptir En onemli ozelligi turevi s displaystyle s ile carpima integrali s displaystyle s ile bolmeye donusturmesidir Yani diferansiyel denklemleri cozmesi daha kolay olan polinomlara donusturur Denklem cozuldukten sonra ters Laplace donusumu ile zaman tanim kumesine tekrar donulebilir Verilen f t ve g t fonksiyonlari ve bunlarin Laplace donusumleri F s ve G s icin f t L 1 F s displaystyle f t mathcal L 1 F s g t L 1 G s displaystyle g t mathcal L 1 G s asagidaki tablo tek yanli Laplace donusumunun ozelliklerinin bir listesidir Tek yanli Laplace donusumunun ozellikleri Zaman tanim Frekans tanim YorumDogrusallik af t bg t displaystyle af t bg t aF s bG s displaystyle aF s bG s Integralin temel kurallariyla kanitlanabilir Frekans Turevlemesi tf t displaystyle tf t F s displaystyle F s Genel Frekans Turevlemesi tnf t displaystyle t n f t 1 nF n s displaystyle 1 n F n s Genel olarakTurevleme f t displaystyle f t sF s f 0 displaystyle sF s f 0 Integralin acik hali yazilip bu integralde kismi integrasyon yontemi kullanilarak bulunabilir Ikinci Turevleme f t displaystyle f t s2F s sf 0 f 0 displaystyle s 2 F s sf 0 f 0 f t displaystyle f t fonksiyonuna Turevleme ozelligi uygulanir Genel Turevleme f n t displaystyle f n t snF s sn 1f 0 f n 1 0 displaystyle s n F s s n 1 f 0 cdots f n 1 0 Ikinci turevle ilgili sonuctan tumevarimla bulunmustur Frekans Entegrasyonu f t t displaystyle frac f t t s F s ds displaystyle int s infty F sigma d sigma Entegrasyon 0tf t dt u t f t displaystyle int 0 t f tau d tau u t f t 1sF s displaystyle 1 over s F s u t displaystyle u t Olcekleme f at displaystyle f at 1 a F sa displaystyle 1 over a F left s over a right Frekans oteleme eatf t displaystyle e at f t F s a displaystyle F s a Zaman oteleme f t a u t a displaystyle f t a u t a e asF s displaystyle e as F s u t displaystyle u t Konvulsiyon f g t 0tf t g t t dt displaystyle f g t int 0 t f tau g t tau d tau F s G s displaystyle F s cdot G s Periyodik Fonksiyon f t displaystyle f t 11 e Ts 0Te stf t dt displaystyle 1 over 1 e Ts int 0 T e st f t dt f t displaystyle f t bir periyodik fonksiyon periyot T displaystyle T soyle ki f t f t T t displaystyle f t f t T forall t Baslangic deger teoremi f 0 lims sF s displaystyle f 0 lim s to infty sF s Son deger teoremi f lims 0sF s displaystyle f infty lim s to 0 sF s Paydanin kokleri sol taraf duzlemindedir son deger teoremi bir fonksiyonun uzun donem davranisini basit kesirlere ayirma veya diger zorlu cebir islemler uygulamaksizin verdigi icin yararlidir Eger bir fonksiyonun kokleri sag taraf duzlemindeyse orn et displaystyle e t or sin t displaystyle sin t bu formulun davranisi tanimsizdir Ayrica bakinizMatematiksel fonksiyonlarin listesi Fourier donusumu Z donusumu Hankel donusumuDis baglantilarhttp wims unice fr wims wims cgi 10 Subat 2008 tarihinde Wayback Machine sitesinde Verilen bir fonksiyonun hem Laplace ve Fourier donusumlerini hem de ters donusumlerini hesaplayan bir site Kaynakca Korn amp Korn 1967 ss 226 227BibliyografyaKorn G A Korn T M 1967 Mathematical Handbook for Scientists and Engineers 2nd McGraw Hill Companies ISBN 978 0 07 035370 1
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans






