Douglas Gough tarafından türetilen bir terim olan Helyosismoloji, Güneş'in yapısını ve dinamiklerini salınımları yoluyla inceleyen bilimdir. Bunlar esas olarak Güneş yüzeyine yakın konveksiyonla sürekli olarak yönlendirilen ve sönümlenen ses dalgalarından kaynaklanır. Sırasıyla Dünya'nın veya yıldızların salınımları yoluyla incelenmesi olan jeosismoloji veya asterosismolojiye (Gough tarafından da türetilmiştir) benzer. Güneş'in salınımları ilk kez 1960'ların başında tespit edilmiş olsa da, salınımların Güneş boyunca yayıldığı ve bilim adamlarının Güneş'in derin iç kısımlarını incelemesine olanak sağlayabileceği ancak 1970'lerin ortalarında fark edildi. Modern alan, Güneş'in rezonans modlarını doğrudan inceleyen küresel helyosismoloji ve bileşen dalgalarının Güneş'in yüzeyine yakın yayılmasını inceleyen yerel helyosismoloji olarak ikiye ayrılmıştır.
Helyosismoloji bir dizi bilimsel buluşa katkıda bulunmuştur. Bunlardan en dikkate değer olanı, Güneş'ten geleceği tahmin edilen nötrino akışının yıldız modellerindeki kusurlardan kaynaklanamayacağını ve bunun yerine parçacık fiziğiyle ilgili bir sorun olması gerektiğini göstermekti. Güneş nötrino sorunu olarak adlandırılan sorun, sonuçta nötrino salınımları ile çözüldü. Nötrino salınımlarının deneysel keşfi, 2015 Nobel Fizik Ödülü'ne layık görüldü. Helyosismoloji aynı zamanda Güneş'in çekim potansiyelinin dört kutuplu (ve daha yüksek dereceli) momentlerinin doğru ölçümlerine de olanak tanıdı; ki, bunlar Genel Görelilik ile tutarlıdır. Güneş'in iç dönüş profiline ilişkin ilk helyosismik hesaplamalar, katı bir şekilde dönen çekirdek ve diferansiyel olarak dönen bir zarf şeklinde kaba bir ayrım göstermiştir. Sınır tabakası artık takoklin olarak bilinmektedir ve için önemli bir bileşen olduğu düşünülmektedir. Her ne kadar kabaca güneş konveksiyon bölgesinin tabanıyla örtüşse de (aynı zamanda helyosismoloji yoluyla da çıkarım yapılıyor), konveksiyon bölgesiyle bağlantılı ve baroklinisite ile Maxwell stresleri arasındaki etkileşim tarafından yönlendirilen meridyensel bir akışın bulunduğu bir sınır katmanı olması nedeniyle kavramsal olarak farklıdır.
Helyosismoloji en çok, ilk olarak Avustralya yazında Güney Kutbu yakınlarından kesintisiz gözlemlerle başlayan, Güneş'in sürekli izlenmesinden yararlanır. Buna ek olarak, çoklu güneş döngüleri üzerinde yapılan gözlemler, helyosismologların Güneş'in yapısındaki onlarca yıl boyunca meydana gelen değişiklikleri incelemesine de olanak tanımıştır. Bu çalışmalar, onlarca yıldır faaliyet gösteren (GONG) ve (BiSON) gibi küresel teleskop ağları tarafından mümkün kılınmaktadır.
Güneş salınımı türleri

Güneş salınımı modları, hidrostatik dengede kabaca küresel simetrik, kendi kendine yerçekimine sahip bir sıvının rezonans titreşimleri olarak yorumlanır. Daha sonra her mod yaklaşık olarak yarıçap 
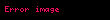
- Radyal düzen olarak bilinen, yarıçaptaki düğüm kabuklarının sayısı
;
- açısal derece olarak bilinen, her küresel kabuktaki düğüm dairelerinin toplam sayısı
; ve
- Azimut sırası olarak bilinen, boyuna olan düğüm dairelerinin sayısı
.
Salınımların iki kategoriye ayrıldığı gösterilebilir: iç salınımlar ve özel bir yüzey salınımları kategorisi. Daha spesifik olarak şunlar vardır:
Basınç modları (p modları)
Basınç modları özünde sabit ses dalgalarıdır. Baskın geri çağırıcı kuvvet (yüzdürme kuvveti yerine) basınçtır, dolayısıyla adı da buradan gelir. İç kısımla ilgili çıkarımlar için kullanılan tüm güneş salınımları p modlarıdır; frekansları yaklaşık 1 ila 5 milihertz arasındadır ve açısal dereceleri sıfırdan (tamamen radyal hareket) ila 

Yerçekimi modları (g modları)
Yerçekimi modları, ışınımsal iç kısım veya atmosfer gibi konvektif olarak kararlı bölgelerle sınırlıdır. Geri çağırıcı kuvvet ağırlıklı olarak kaldırma kuvvetidir ve dolayısıyla dolaylı olarak yer çekimidir, ki isimleri de buradan gelir. Konveksiyon bölgesinde hızla kaybolurlar ve bu nedenle iç modların yüzeyde küçük genlikleri vardır ve tespit edilmesi ve tanımlanması son derece zordur. Sadece birkaç g modunun ölçümünün bile Güneş'in derin iç kısmına ilişkin bilgimizi önemli ölçüde artırabileceği uzun zamandır bilinmektedir. Bununla birlikte, dolaylı tespitler hem iddia edilmiş hem de bunlara karşı çıkılmış olmasına rağmen, hiçbir bireysel g modu henüz kesin olarak ölçülmemiştir. Ayrıca, konvektif olarak kararlı atmosferle sınırlı benzer yerçekimi modları da olabilir.
Yüzey yerçekimi modları (f modları)
Yüzey yerçekimi dalgaları derin sudaki dalgalara benzer ve Lagrangian basınç pertürbasyonunun esasen sıfır olması özelliğine sahiptir.Yüksek derecedeki 






Sismoloji neyi ortaya çıkarabilir?
Sismolojide başarıyla kullanılan salınımlar esasen adyabatiktir. Bu nedenle dinamikleri, basınç kuvvetlerinin 
















Veri analizi
Küresel helyosismoloji



 ) SOHO gemisindeki MDI cihazından alınan 144 günlük veriler üzerinden hesaplanan güneş salınımları. Renk skalası logaritmiktir ve modları daha görünür kılmak için sinyaldeki maksimum gücün yüzde birine doymuştur. Düşük frekanslı bölgeye granülasyon sinyali hakimdir. Açısal derece arttıkça, bireysel mod frekansları, her biri bir dizi düşük dereceli modlara karşılık gelen net sırtlar üzerinde birleşir.
) SOHO gemisindeki MDI cihazından alınan 144 günlük veriler üzerinden hesaplanan güneş salınımları. Renk skalası logaritmiktir ve modları daha görünür kılmak için sinyaldeki maksimum gücün yüzde birine doymuştur. Düşük frekanslı bölgeye granülasyon sinyali hakimdir. Açısal derece arttıkça, bireysel mod frekansları, her biri bir dizi düşük dereceli modlara karşılık gelen net sırtlar üzerinde birleşir.Ham sismik verileri analiz etmenin başlıca aracı Fourier dönüşümüdür. İyi bir yaklaşımla, her mod, frekansın bir fonksiyonu olarak gücün bir Lorentz fonksiyonu olduğu sönümlü bir harmonik osilatördür. Uzaysal olarak çözülmüş veriler genellikle daha sonra Fourier dönüşümüne tabi tutulan zaman serilerini elde etmek için istenen küresel harmoniklere yansıtılır. Helyosismologlar tipik olarak ortaya çıkan tek boyutlu güç spektrumlarını iki boyutlu bir spektrumda birleştirirler.
Salınımların düşük frekans aralığı, neden olduğu varyasyonların hakimiyetindedir. Modların analiz edilmesinden önce (veya aynı zamanda) bunun filtrelenmesi gerekir. Güneş yüzeyindeki granüler akışlar, yükselen granüllerin merkezlerinden aralarındaki dar aşağı yönlü akımlara kadar çoğunlukla yataydır. Salınımlara bağlı olarak granülasyon, yoğunluk açısından görüş hattı hızından daha güçlü bir sinyal üretir, bu nedenle ikincisi, helyosismik gözlemevleri için tercih edilir.
Yerel helyosismoloji
Charles Lindsey, Doug Braun ve Stuart Jefferies tarafından 1993'te türetilen bir terim olan yerel helyosismoloji, gözlemsel verilerden çıkarımlar yapmak için birkaç farklı analiz yöntemini kullanır.
- Fourier-Hankel spektral yöntemi ilk olarak güneş lekelerinin dalga emilimini araştırmak için kullanılmıştır.
- İlk olarak Frank Hill tarafından tanıtılan halka diyagramı analizi, güneş ışınlarının yamaları üzerinde hesaplanan güneş salınımlarının güç spektrumlarından ortamdaki akustik dalgaların Doppler kaymalarını gözlemleyerek güneş yüzeyinin altındaki yatay akışların hızını ve yönünü (tipik olarak 15° × 15°) çıkarmak için kullanılır. Bu nedenle, halka diyagramı analizi, Güneş üzerindeki yerel alanlara (Güneş'in yarısının aksine) uygulanan küresel helyosismolojinin bir genellemesidir. Örneğin ses hızı ve adyabatik indeks, manyetik olarak aktif ve aktif olmayan (sessiz Güneş) bölgelerde karşılaştırılabilir.
- Zaman-mesafe heliosismolojisi güneş dalgalarının güneş yüzeyindeki herhangi iki konum arasındaki seyahat sürelerini ölçmeyi ve yorumlamayı amaçlamaktadır. İki konumu birbirine bağlayan ışın yolunun yakınındaki homojensizlikler, bu iki nokta arasındaki seyahat süresini bozar. Güneş iç kısmının yerel yapısını ve dinamiklerini anlamak için ters bir problemin çözülmesi gerekir.
- Uzak taraf (manyetik) görüntüleme amacıyla Charles Lindsey ve Doug Braun tarafından ayrıntılı olarak tanıtılan helyosismik holografi, faza duyarlı holografinin özel bir durumudur. Buradaki fikir, Güneş'in uzak tarafındaki aktif bölgeler hakkında bilgi edinmek için görünür diskteki dalga alanını kullanmaktır. Helyosismik holografideki temel fikir, dalga alanının, örneğin güneş yüzeyinde gözlemlenen görüş hattı Doppler hızının, herhangi bir zamanda güneşin iç kısmındaki herhangi bir konumdaki dalga alanının tahminini yapmak için kullanılabilmesidir. Bu anlamda holografi, jeofizikte 1940'lardan bu yana kullanılan bir teknik olan çok benzer. Başka bir örnek olarak bu teknik, bir güneş patlamasının sismik görüntüsünü vermek için kullanılmıştır.
- Doğrudan modellemede amaç, Fourier alanındaki dalga alanında görülen frekans-dalga sayısı korelasyonlarının doğrudan ters çevrilmesinden yeraltı akışlarını tahmin etmektir. Woodard tekniğin yüzeye yakın akışları f modlarında geri kazanma yeteneğini göstermiştir.
İnversiyon
Giriş
Güneş'in salınım modları, onun sürekli yapısına duyarlı ayrık bir dizi gözlemi temsil eder. Bu, bilim adamlarının Güneş'in iç yapısı ve dinamiği için formüle etmelerine olanak tanır. Güneş'in bir referans modeli göz önüne alındığında, mod frekansları ile Güneş'in mod frekansları arasındaki farklar, eğer küçükse, Güneş'in yapısı ile referans modelin yapısı arasındaki farkların ağırlıklı ortalamalarıdır. Frekans farklılıkları daha sonra bu yapısal farklılıkları anlamak için kullanılabilir. Bu ortalamaların ağırlıklandırma fonksiyonları çekirdekler olarak bilinir.
Yapı
Güneş'in yapısının ilk ters çevrilmeleri Duvall yasası kullanılarak yapılmıştı ve daha sonra bir referans güneş modeli etrafında doğrusallaştırılan Duvall yasası kullanılarak yapıldı. Bu sonuçlar daha sonra teorik bir referans modeli hakkındaki yıldız salınımlarını tanımlayan denklemlerin tam setini doğrusallaştıran analizlerle desteklenmiştir ve artık frekans verilerini tersine çevirmenin standart bir yolu haline gelmiştir. Ters çevirmeler, güneş modellerindeki farklılıkları gösterir; bunlar, yerçekimsel çökelmenin uygulanmasıyla büyük ölçüde azaltılmıştır: daha ağır elementlerin güneş merkezine doğru kademeli olarak ayrılması (ve bunların yerini almak üzere daha hafif elementlerin yüzeye çıkması).
Döndürme

Eğer Güneş tamamen küresel olsaydı, farklı azimut dereceleri m olan modlar aynı frekanslara sahip olurdu. Ancak dönüş, bu bozulmayı kırar ve modların frekansları, Güneş'teki açısal hızın ağırlıklı ortalamaları olan dönüşsel bölünmelerle farklılık gösterir. Farklı modlar Güneş'in farklı bölgelerine duyarlıdır ve yeterli veri verildiğinde, bu farklar Güneş boyunca dönüş hızını anlamak için kullanılabilir. Örneğin, Güneş her yerinde düzgün bir şekilde dönüyor olsaydı, tüm p modları yaklaşık olarak aynı miktarda bölünürdü. Aslında ekvatorun kutuplardan daha hızlı döndüğü yüzeyde görüldüğü gibi açısal hız düzgün değildir. Güneş, küresel, dönmeyen bir modelin, dönen çekirdeklerin türetilmesi için gerçeğe yeterince yakın olmasını sağlayacak kadar yavaş döner.
Helyoseismoloji, Güneş'in çeşitli özelliklere sahip bir dönme profiline sahip olduğunu göstermiştir:
- iç çekirdeğin dönüş hızı iyi bilinmemekle birlikte, katı şekilde dönen ışınımlı (yani konvektif olmayan) bir bölge;
- rijit bir şekilde dönen iç kısım ile diferansiyel olarak dönen konvektif kabuğu ayıran, takoklin olarak bilinen ince bir kesme katmanı;
- dönüş hızının hem derinliğe hem de enleme göre değiştiği konvektif bir zarf; ve
- Yüzeyin hemen altında, dönme hızının yüzeye doğru yavaşladığı son kayma tabakası.
Diğer alanlarla ilişki
Jeosismoloji
Helyosismoloji, jeosismoloji ile benzerlikten doğmuştur ancak bazı önemli farklılıklar devam etmektedir. Birincisi, Güneş'in katı bir yüzeyi yoktur ve bu nedenle kayma dalgalarını destekleyemez. Veri analizi perspektifinden bakıldığında küresel helyosismoloji, yalnızca normal modları incelemesi nedeniyle jeosismolojiden farklılık gösterir. Dolayısıyla yerel helyosismoloji, dalga alanının tamamını incelemesi anlamında jeosismolojiye ruhen biraz daha yakındır.
Asterosismoloji
Güneş bir yıldız olduğu için helyosismoloji, asterosismoloji olarak bilinen diğer yıldızlardaki salınımların incelenmesiyle yakından ilgilidir. Helyoseismoloji, salınımları aynı zamanda olarak bilinen dış konveksiyon bölgeleri tarafından yönlendirilen ve sönümlenen yıldızların incelenmesiyle en yakından ilişkilidir, ancak temeldeki teori diğer değişken yıldız sınıfları için genel olarak aynıdır.
Temel fark uzak yıldızlardaki salınımların çözülememesidir. Küresel harmoniğin daha parlak ve daha karanlık sektörleri iptal edildiğinden, bu durum asterosismolojiyi neredeyse tamamen düşük dereceli modların (açısal derece 
Tarih
Güneş salınımları ilk olarak 1960'ların başında yaklaşık 5 dakikalık bir periyotla yarı periyodik yoğunluk ve görüş hattı hız değişimi olarak gözlemlenmiştir. Bilim adamları yavaş yavaş salınımların Güneş'in küresel modları olabileceğini fark ettikten sonra, modların iki boyutlu güç spektrumunda net sırtlar oluşturacağı öngörüldü. Sırtların oluştuğu daha sonra 1970'lerin ortalarında yüksek dereceli modların gözlemleri sırasında doğrulandı ve farklı radyal düzenlerin mod çokluları tam disk gözlemlerinde ayırt edilebildi. Hemen hemen aynı tarihlerde, ve Douglas Gough, Güneş'in iç yapısını anlamak için bireysel mod frekanslarını kullanma potansiyelini öne sürdüler. Güneş modellerini düşük dereceli verilere göre kalibre ederek, biri düşük 




1980'lerde geliştirilen yeni ters çevirme yöntemleri, araştırmacıların Güneş'in büyük bölümünde ses hızı ve daha az doğru bir şekilde yoğunluk profilleri hakkında çıkarım yapmasına olanak tanıyarak, nötrino sorununun nedeninin güneş yapısı çıkarımındaki kalıcı hataların olmadığı sonucunu doğruluyor. On yılın sonuna doğru gözlemler, salınım modu frekanslarının Güneş'in manyetik aktivite döngüsüne göre değiştiğini de göstermeye başlamıştır.
Geceleri Güneş'i gözlemleyememe sorununun üstesinden gelmek için, birkaç grup (örneğin, kısaca BiSON, ve ) Güneş'in her zaman en az bir düğüm tarafından görülebileceği teleskop ağları kurmaya başlamıştı. Uzun, kesintisiz gözlemler alanı olgunluğa eriştirdi ve alanın durumu Science dergisinin 1996 yılındaki özel sayısında özetlendi. Bu, helyosismoloji için yüksek kaliteli veriler üretmeye başlayan Güneş ve Heliosferik Gözlemevi'nin (SoHO) normal operasyonlarının başlamasıyla aynı zamana denk gelmişti.
Sonraki yıllarda güneş nötrinosu sorununun çözüldüğü görüldü ve uzun sismik gözlemler, birden fazla güneş aktivite döngüsünün analizine izin vermeye başladı. Standart güneş modelleri ile helyosismik inversiyonlar arasındaki uyum, ayrıntılı üç boyutlu modellere dayalı olarak güneş fotosferindeki ağır element içeriğinin yeni ölçümleriyle bozuldu. Her ne kadar sonuçlar daha sonra 1990'larda kullanılan geleneksel değerlere doğru kaymış olsa da, yeni bolluklar, modeller ile helyosismik inversiyonlar arasındaki uyumu önemli ölçüde kötüleştirdi. Tutarsızlığın nedeni çözülememişti ve güneş bolluğu problemi olarak bilinmektedir.
SoHO'nun uzay tabanlı gözlemleri devam etti ve 2010 yılında SoHO'ya, faaliyetlerine başladığı günden bu yana Güneş'i sürekli olarak izleyen Güneş Dinamikleri Gözlemevi (SDO) de katıldı. Ek olarak, yer tabanlı ağlar (özellikle BiSON ve GONG) çalışmaya devam ederek yerden de neredeyse sürekli veri sağlamaktadır.
Ayrıca bakınız
Kaynakça
- ^ Gough, D.O.; Kosovichev, A.G.; Toomre, J.; ve diğerleri. (1996), "The seismic structure of the Sun", Science, 272 (5266), ss. 1296-1300, doi:10.1126/science.272.5266.1296, (PMID) 8662458
- ^ a b Gizon, L.; Birch, A. C. (2005), "Local Helioseismology", Living Reviews in Solar Physics, 2 (1), s. 6, doi:10.12942/lrsp-2005-6
- ^ Fukuda, Y.; Super-Kamiokande Collaboration (1998), "Evidence for oscillation of atmospheric neutrinos", Phys. Rev. Lett., 81 (8), ss. 1562-1567, arXiv:hep-ex/9807003 $2, doi:10.1103/PhysRevLett.81.1562
- ^ Bahcall, J. N.; Concha, Gonzalez-Garcia M.; Pe, na-Garay C. (2001), "Global analysis of solar neutrino oscillations including SNO CC measurement", Journal of High Energy Physics, 2001 (8), s. 014, arXiv:hep-ph/0106258 $2, doi:10.1088/1126-6708/2001/08/014
- ^ Bahcall, J. N. (2001), "High-energy physics: Neutrinos reveal split personalities", Nature, 412 (6842), ss. 29-31, doi:10.1038/35083665, (PMID) 11452285
- ^ Webb, Jonathan (6 Ekim 2015). "Neutrino 'flip' wins physics Nobel Prize". BBC News. 15 Nisan 2022 tarihinde kaynağından . Erişim tarihi: 28 Eylül 2023.
- ^ Duvall, T.L.,Jr; Dziembowski, W.A.; Goode, P.R.; Gough, D.O.; Harvey, J.W.; Leibacher, J.W. (1984), "The internal rotation of the Sun", Nature, 310 (5972), ss. 22-25, doi:10.1038/310022a0
- ^ Pijpers, F.P. (1998), "Helioseismic determination of the solar gravitational quadrupole moment", Mon. Not. R. Astron. Soc., 297 (3), ss. L76-L80, arXiv:astro-ph/9804258 $2, doi:10.1046/j.1365-8711.1998.01801.x
- ^ Antia, H.M.; Chitre, S.M.; Gough, D.O. (2008), "Temporal variations in the Sun's rotational kinetic energy", Astron. Astrophys., 477 (2), ss. 657-663, arXiv:0711.0799 $2, doi:10.1051/0004-6361:20078209
- ^ Spiegel, E. A.; Zahn, J.-P. (1992), "The solar tachocline", Astronomy and Astrophysics, 265, s. 106
- ^ Fan, Y. (2009), "Magnetic Fields in the Solar Convection Zone", Living Reviews in Solar Physics, 6 (1), s. 4, doi:10.12942/lrsp-2009-4
- ^ Gough, D.O.; McIntyre, M.E. (1998), "Inevitability of a magnetic field in the Sun's interior", Nature, 394 (6695), s. 755, doi:10.1038/29472
- ^ a b Grec, G.; Fossat, E.; Pomerantz, M. (1980), "Solar oscillations: full disk observations from the geographic South Pole", Nature, 288 (5791), ss. 541-544, doi:10.1038/288541a0
- ^ a b Duvall, Jr. T. L.; Harvey, J. W. (1983), "Observations of solar oscillations of low and intermediate degree", Nature, 302 (5903), s. 24, doi:10.1038/302024a0
- ^ Christensen-Dalsgaard, J.; Dappen, W.; Ajukov, S. V.; Anderson, E. R.; Antia, H. M.; Basu, S.; Baturin, V. A.; Berthomieu, G.; Chaboyer, B.; Chitre, S. M. (1996), "The Current State of Solar Modeling", Science, 272 (5266), ss. 1286-92, doi:10.1126/science.272.5266.1286, (PMID) 8662456
- ^ Christensen-Dalsgaard, J.; Dappen, W.; Ajukov, S. V. and (1996), "The Current State of Solar Modeling", Science, 272 (5266), ss. 1286-1292, doi:10.1126/science.272.5266.1286, (PMID) 8662456
- ^ Appourchaux, T.; Belkacem, K.; Broomhall, A.-M.; Chaplin, W. J.; Gough, D. O.; Houdek, G.; Provost, J.; Baudin, F.; Boumier, P.; Elsworth, Y. (2010), "The quest for the solar g modes", Astronomy and Astrophysics Review, 18 (1–2), s. 197, arXiv:0910.0848 $2, doi:10.1007/s00159-009-0027-z
- ^ a b Gough, D.O. (1984), "Solar inverse theory", Solar Seismology from Space (Ed. R.K. Ulrich, JPL Publ., Pasadena), 84-84, ss. 49-78
- ^ Garc\'\ia, R. A.; Turck-Chi\`eze, S.; Jiménez-Reyes, S. J.; Ballot, J.; Pallé, P. L.; Eff-Darwich, A.; Mathur, S.; Provost, J. (2007), "Tracking Solar Gravity Modes: The Dynamics of the Solar Core", Science, 316 (5831), ss. 1591-3, doi:10.1126/science.1140598, (PMID) 17478682
- ^ Fossat, E.; Boumier, P.; Corbard, T.; Provost, J.; Salabert, D.; Schmider, F. X.; Gabriel, A. H.; Grec, G.; Renaud, C.; Robillot, J. M. (2017), "Asymptotic g modes: Evidence for a rapid rotation of the solar core", Astronomy and Astrophysics, 604, ss. A40, arXiv:1708.00259 $2, doi:10.1051/0004-6361/201730460
- ^ Schunker, H.; Schou, J.; Gaulme, P.; Gizon, L. (2018), "Fragile Detection of Solar g-Modes by Fossat et al.", Solar Physics, 293 (6), s. 95, arXiv:1804.04407 $2, doi:10.1007/s11207-018-1313-6
- ^ Scherrer, P. H.; Gough, D. O. (2019), "A critical evaluation of recent claims concerning solar rotation", Astrophysical Journal, 877 (1), ss. 42-53, arXiv:1904.02820 $2, doi:10.3847/1538-4357/ab13ad
- ^ Gough, D.O. (1982), "A review of the theory of solar oscillations and its implications concerning the internal structure of the Sun", In Pulsations in Classical and Cataclysmic Variable Stars (Ed. J.P. Cox & C.J. Hansen, JILA, Boulder), ss. 117-137
- ^ Gough, D.O. (2003), "What have we learned from helioseismology, what have we really learned, and what do we aspire to learn?", Solar Physics, 287 (1–2), ss. 9-41, arXiv:1210.0820 $2, doi:10.1007/s11207-012-0099-1
- ^ Kosovichev, A.G.; Christensen-Dalsgaard, J.; Däeppen, W.; Dziembowski, W.A.; Gough, D.O.; Thompson, M.J. (1992), "Sources of uncertainty in direct seismological measurements of the solar helium abundance", Mon. Not. R. Astron. Soc., 259 (3), ss. 536-558, Bibcode:1992MNRAS.259..536K, doi:10.1093/mnras/259.3.536
- ^ Houdek, G.; Gough, D.O. (2011), "On the seismic age and heavy-element abundance of the Sun", Mon. Not. R. Astron. Soc., 418 (2), ss. 1217-1230, arXiv:1108.0802 $2, Bibcode:2011MNRAS.418.1217H, doi:10.1111/j.1365-2966.2011.19572.x
- ^ Rhodes, Jr. E. J.; Kosovichev, A. G.; Schou, J.; ve diğerleri. (1997), "Measurements of Frequencies of Solar Oscillations from the MDI Medium-l Program", Solar Physics, 175 (2), s. 287, doi:10.1023/A:1004963425123
- ^ Lindsey, C.; Braun, D.C.; Jefferies, S.M. (Ocak 1993). T.M. Brown (Ed.). "Local Helioseismology of Subsurface Structure" in "GONG 1992. Seismic Investigation of the Sun and Stars". GONG 1992. Seismic Investigation of the Sun and Stars. Proceedings of a Conference Held in Boulder. Astronomical Society of the Pacific Conference Series. 42. ss. 81-84. ISBN .
- ^ Braun, D.C.; Duvall Jr., T.L.; Labonte, B.J. (Ağustos 1987). "Acoustic absorption by sunspots". The Astrophysical Journal. 319: L27-L31. doi:10.1086/184949.
- ^ Hill, F. (Ekim 1988). "Rings and trumpets - Three-dimensional power spectra of solar oscillations". Astrophysical Journal. 333: 996-1013. doi:10.1086/166807.
- ^ Basu, S.; Antia, H.M.; Bogart, R.S. (Ağustos 2004). "Ring-Diagram Analysis of the Structure of Solar Active Regions". The Astrophysical Journal. 610 (2): 1157-1168. doi:10.1086/421843.
- ^ Duvall Jr., T.L.; Jefferies, S.M.; Harvey, J.W.; Pomerantz, M.A. (Nisan 1993). "Time-distance helioseismology". Nature. 362 (6419): 430-432. doi:10.1038/362430a0.
- ^ Jensen, J. M. (2003), "Time-distance: what does it tell us?", Gong+ 2002. Local and Global Helioseismology: The Present and Future, 517, s. 61
- ^ Braun, D. C.; Lindsey, C. (2001), "Seismic Imaging of the Far Hemisphere of the Sun", Astrophysical Journal Letters, 560 (2), ss. L189, doi:10.1086/324323
- ^ Donea, A.-C.; Braun, D.C.; Lindsey, C. (Mart 1999). "Seismic Images of a Solar Flare". The Astrophysical Journal. 513 (2): L143-L146. doi:10.1086/311915.
- ^ Woodard, M. F. (Ocak 2002). "Solar Subsurface Flow Inferred Directly from Frequency-Wavenumber Correlations in the Seismic Velocity Field". The Astrophysical Journal. 565 (1): 634-639. doi:10.1086/324546.
- ^ Christensen-Dalsgaard, J.; Duvall, Jr. T. L.; Gough, D. O.; Harvey, J. W.; Rhodes, Jr. E. J. (1985), "Speed of sound in the solar interior", Nature, 315 (6018), s. 378, doi:10.1038/315378a0
- ^ Christensen-Dalsgaard, J.; Thompson, M. J.; Gough, D. O. (1989), "Differential asymptotic sound-speed inversions", MNRAS, 238 (2), ss. 481-502, doi:10.1093/mnras/238.2.481
- ^ Dziembowski, W.A.; Pamyatnykh, A.A.; Sienkiewicz, R. (1990), "Solar model from helioseismology and the neutrino flux problem", Mon. Not. R. Astron. Soc., 244, ss. 542-550
- ^ Antia, H. M.; Basu, S. (1994), "Nonasymptotic helioseismic inversion for solar structure.", Astronomy & Astrophysics Supplement Series, 107, s. 421
- ^ Gough, D.O.; Thompson, M.J. (1991), "The inversion problem", M. S. Matthews; W. C. Livingston (Ed.), Solar interior and atmosphere, Tucson: University of Arizona Press, ss. 519-561
- ^ Basu, S. (2016), "Global seismology of the Sun", Living Reviews in Solar Physics, 13 (1), s. 2, arXiv:1606.07071 $2, doi:10.1007/s41116-016-0003-4
- ^ Cox, A. N.; Guzik, J. A.; Kidman, R. B. (1989), "Oscillations of solar models with internal element diffusion", Astrophysical Journal, 342, s. 1187, doi:10.1086/167675, 28 Eylül 2023 tarihinde kaynağından , erişim tarihi: 28 Eylül 2023
- ^ Christensen-Dalsgaard, J.; Proffitt, C. R.; Thompson, M. J. (1993), "Effects of diffusion on solar models and their oscillation frequencies" (PDF), Astrophysical Journal Letters, 403, ss. L75, doi:10.1086/186725, 23 Mart 2022 tarihinde kaynağından (PDF), erişim tarihi: 28 Eylül 2023
- ^ Thompson, M. J.; Christensen-Dalsgaard, J.; Miesch, M. S.; Toomre, J. (2003), "The Internal Rotation of the Sun", Annual Review of Astronomy & Astrophysics, 41, ss. 599-643, doi:10.1146/annurev.astro.41.011802.094848
- ^ Beck, J. G. (2000), "A comparison of differential rotation measurements - (Invited Review)", Solar Physics, 191 (1), ss. 47-70, doi:10.1023/A:1005226402796
- ^ Howe, R. (2009), "Solar Interior Rotation and its Variation", Living Reviews in Solar Physics, 6 (1), s. 1, arXiv:0902.2406 $2, doi:10.12942/lrsp-2009-1
- ^ Leighton, R. B.; Noyes, R. W.; Simon, G. W. (1962), "Velocity Fields in the Solar Atmosphere. I. Preliminary Report.", Astrophysical Journal, 135, s. 474, doi:10.1086/147285
- ^ Evans, J. W.; Michard, R. (1962), "Observational Study of Macroscopic Inhomogeneities in the Solar Atmosphere. III. Vertical Oscillatory Motions in the Solar Photosphere.", Astrophysical Journal, 136, s. 493, doi:10.1086/147403
- ^ Leibacher, J. W.; Stein, R. F. (1971), "A New Description of the Solar Five-Minute Oscillation", Astrophysical Letters, 7, s. 191
- ^ Ulrich, R. K. (1970), "The Five-Minute Oscillations on the Solar Surface", Astrophysical Journal, 162, s. 993, doi:10.1086/150731
- ^ Deubner, F.-L. (1975), "Observations of low wavenumber nonradial eigenmodes of the sun", Astronomy and Astrophysics, 44 (2), s. 371
- ^ Rhodes, Jr. E. J.; Ulrich, R. K.; Simon, G. W. (1977), "Observations of nonradial p-mode oscillations on the sun", Astrophysical Journal, 218, s. 901, doi:10.1086/155745
- ^ Claverie, A.; Isaak, G. R.; McLeod, C. P.; van, der Raay H. B.; Cortes, T. R. (1979), "Solar structure from global studies of the 5-minute oscillation", Nature, 282 (5739), ss. 591-594, doi:10.1038/282591a0
- ^ Christensen-Dalsgaard, J.; Gough, D. O. (1976), "Towards a heliological inverse problem", Nature, 259 (5539), s. 89, doi:10.1038/259089a0
- ^ Christensen-Dalsgaard, J.; Gough, D. O. (1981), "Comparison of the observed solar whole-disk oscillation frequencies with the predictions of a sequence of solar models", Astron. Astrophys., 104 (2), ss. 173-176
- ^ Gough, D.O. (1977), "Random remarks on solar hydrodynamics", Proc. IAU Colloq. 36, ss. 3-36
- ^ Rhodes, Jr. E. J.; Ulrich, R. K. (1977), "The sensitivity of nonradial p mode eigenfrequencies to solar envelope structure", Astrophysical Journal, 218, ss. 521-529, doi:10.1086/155705
- ^ Libbrecht, K. G.; Woodard, M. F. (1990), "Solar-cycle effects on solar oscillation frequencies", Nature, 345 (6278), s. 779, doi:10.1038/345779a0
- ^ Aindow, A.; Elsworth, Y. P.; Isaak, G. R.; McLeod, C. P.; New, R.; Vanderraay, H. B. (1988), "The current status of the Birmingham solar seismology network", Seismology of the Sun and Sun-Like Stars, 286, s. 157
- ^ Chaplin, W. J.; Elsworth, Y.; Howe, R.; Isaak, G. R.; McLeod, C. P.; Miller, B. A.; van, der Raay H. B.; Wheeler, S. J.; New, R. (1996), "BiSON Performance", Solar Physics, 168 (1), s. 1, doi:10.1007/BF00145821
- ^ Harvey, J. W.; Hill, F.; Kennedy, J. R.; Leibacher, J. W.; Livingston, W. C. (1988), "The Global Oscillation Network Group (GONG)", Advances in Space Research, 8 (11), s. 117, doi:10.1016/0273-1177(88)90304-3)
- ^ "Special Issue: GONG Helioseismology", Science, 272 (5266), 1996, 20 Ağustos 2023 tarihinde kaynağından , erişim tarihi: 28 Eylül 2023
- ^ Chaplin, W. J.; Elsworth, Y.; Miller, B. A.; Verner, G. A.; New, R. (2007), "Solar p-Mode Frequencies over Three Solar Cycles", Astrophysical Journal, 659 (2), s. 1749, doi:10.1086/512543
- ^ Bahcall, J. N.; Pinsonneault, M. H.; Basu, S. (2001), "Solar Models: Current Epoch and Time Dependences Neutrinos and Helioseismological Properties", Astrophysical Journal, 555 (2), ss. 990-1012, arXiv:astro-ph/0010346 $2, doi:10.1086/321493
- ^ Asplund, M.; Grevesse, N.; Sauval, A. J. (2005), "The Solar Chemical Composition", Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, 336, s. 25
- ^ Asplund, M.; Grevesse, N.; Sauval, A. J.; Scott, P. (2009), "The Chemical Composition of the Sun", Annual Review of Astronomy & Astrophysics, 47 (1), ss. 481-522, arXiv:0909.0948 $2, doi:10.1146/annurev.astro.46.060407.145222
- ^ Bahcall, J. N.; Basu, S.; Pinsonneault, M.; Serenelli, A. M. (2005), "Helioseismological Implications of Recent Solar Abundance Determinations", Astrophysical Journal, 618 (2), ss. 1049-1056, arXiv:astro-ph/0407060 $2, doi:10.1086/426070
- ^ Gough, D.O. (2003), "What have we learned from helioseismology, what have we really learned, and what do we aspire to learn?", Solar Physics, 287 (1–2), ss. 9-41, arXiv:1210.0820 $2, doi:10.1007/s11207-012-0099-1
Dış bağlantılar
- Kasım 2009'da alındı
- Gough, D.O. (2003). "Solar Neutrino Production". Annales Henri Poincaré. 4 (S1): 303-317. Bibcode:2003AnHP....4..303G. doi:10.1007/s00023-003-0924-z.
- Gizon, Laurent; Birch, Aaron C. (2005). "Local Helioseismology". Living Rev. Sol. Phys. 2 (1): 6. Bibcode:2005LRSP....2....6G. doi:10.12942/lrsp-2005-6.
- Bilim Adamları Bir Sonraki Güneş Lekesi Döngüsüyle İlgili Benzeri Görülmemiş Tahminler Yayınladı Ulusal Bilim Vakfı basın açıklaması, 6 Mart 2006
- Miesch, Mark S. (2005). "Large-Scale Dynamics of the Convection Zone and Tachocline". Living Rev. Sol. Phys. 2 (1): 1. Bibcode:2005LRSP....2....1M. doi:10.12942/lrsp-2005-1.
- Güneş'in Uzak Taraf ve Dünya Tarafı görüntüleri
- Güneş Fiziğinde Yaşayan İncelemeler
- MPS'de Helyosismoloji ve Asterosismoloji
Uydu araçları
- VIRGO
- SOI/MDI
- SDO/HMI
Yer bazlı aletler
- BISON
- Mark-1
- GONG
- HiDHN
Daha fazla okuma
- Christensen-Dalsgaard, Jørgen. . 21 Şubat 2003 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Haziran 2015.
- Pijpers, Frank P. (2006). Methods in Helio- and Asteroseismology. Londra: Imperial College Press. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Douglas Gough tarafindan turetilen bir terim olan Helyosismoloji Gunes in yapisini ve dinamiklerini salinimlari yoluyla inceleyen bilimdir Bunlar esas olarak Gunes yuzeyine yakin konveksiyonla surekli olarak yonlendirilen ve sonumlenen ses dalgalarindan kaynaklanir Sirasiyla Dunya nin veya yildizlarin salinimlari yoluyla incelenmesi olan jeosismoloji veya asterosismolojiye Gough tarafindan da turetilmistir benzer Gunes in salinimlari ilk kez 1960 larin basinda tespit edilmis olsa da salinimlarin Gunes boyunca yayildigi ve bilim adamlarinin Gunes in derin ic kisimlarini incelemesine olanak saglayabilecegi ancak 1970 lerin ortalarinda fark edildi Modern alan Gunes in rezonans modlarini dogrudan inceleyen kuresel helyosismoloji ve bilesen dalgalarinin Gunes in yuzeyine yakin yayilmasini inceleyen yerel helyosismoloji olarak ikiye ayrilmistir Helyosismoloji bir dizi bilimsel bulusa katkida bulunmustur Bunlardan en dikkate deger olani Gunes ten gelecegi tahmin edilen notrino akisinin yildiz modellerindeki kusurlardan kaynaklanamayacagini ve bunun yerine parcacik fizigiyle ilgili bir sorun olmasi gerektigini gostermekti Gunes notrino sorunu olarak adlandirilan sorun sonucta notrino salinimlari ile cozuldu Notrino salinimlarinin deneysel kesfi 2015 Nobel Fizik Odulu ne layik goruldu Helyosismoloji ayni zamanda Gunes in cekim potansiyelinin dort kutuplu ve daha yuksek dereceli momentlerinin dogru olcumlerine de olanak tanidi ki bunlar Genel Gorelilik ile tutarlidir Gunes in ic donus profiline iliskin ilk helyosismik hesaplamalar kati bir sekilde donen cekirdek ve diferansiyel olarak donen bir zarf seklinde kaba bir ayrim gostermistir Sinir tabakasi artik takoklin olarak bilinmektedir ve icin onemli bir bilesen oldugu dusunulmektedir Her ne kadar kabaca gunes konveksiyon bolgesinin tabaniyla ortusse de ayni zamanda helyosismoloji yoluyla da cikarim yapiliyor konveksiyon bolgesiyle baglantili ve baroklinisite ile Maxwell stresleri arasindaki etkilesim tarafindan yonlendirilen meridyensel bir akisin bulundugu bir sinir katmani olmasi nedeniyle kavramsal olarak farklidir Helyosismoloji en cok ilk olarak Avustralya yazinda Guney Kutbu yakinlarindan kesintisiz gozlemlerle baslayan Gunes in surekli izlenmesinden yararlanir Buna ek olarak coklu gunes donguleri uzerinde yapilan gozlemler helyosismologlarin Gunes in yapisindaki onlarca yil boyunca meydana gelen degisiklikleri incelemesine de olanak tanimistir Bu calismalar onlarca yildir faaliyet gosteren GONG ve BiSON gibi kuresel teleskop aglari tarafindan mumkun kilinmaktadir Gunes salinimi turleriRadyal derece n 14 acisal derece l 20 ve azimut derecesi m 16 olan bir gunes basinci modunun p modu gosterimi Yuzey karsilik gelen kuresel harmonigi gosterir Ic kisim standart bir gunes modeli kullanilarak hesaplanan radyal yer degistirmeyi gostermektedir Dalgalar gunesin merkezine yaklastikca ses hizindaki artisin akustik dalga boyunda da buna karsilik gelen bir artisa neden oldugunu unutmayin Gunes salinimi modlari hidrostatik dengede kabaca kuresel simetrik kendi kendine yercekimine sahip bir sivinin rezonans titresimleri olarak yorumlanir Daha sonra her mod yaklasik olarak yaricap r displaystyle r fonksiyonunun carpimi ve kuresel bir harmonik Ylm 8 ϕ displaystyle Y l m theta phi olarak temsil edilebilir ve sonuc olarak asagidakileri etiketleyen uc kuantum sayisiyla karakterize edilebilir Radyal duzen olarak bilinen yaricaptaki dugum kabuklarinin sayisi n displaystyle n acisal derece olarak bilinen her kuresel kabuktaki dugum dairelerinin toplam sayisi ℓ displaystyle ell ve Azimut sirasi olarak bilinen boyuna olan dugum dairelerinin sayisi m displaystyle m Salinimlarin iki kategoriye ayrildigi gosterilebilir ic salinimlar ve ozel bir yuzey salinimlari kategorisi Daha spesifik olarak sunlar vardir Basinc modlari p modlari Basinc modlari ozunde sabit ses dalgalaridir Baskin geri cagirici kuvvet yuzdurme kuvveti yerine basinctir dolayisiyla adi da buradan gelir Ic kisimla ilgili cikarimlar icin kullanilan tum gunes salinimlari p modlaridir frekanslari yaklasik 1 ila 5 milihertz arasindadir ve acisal dereceleri sifirdan tamamen radyal hareket ila 103 displaystyle 10 3 mertebesine kadar degisir Genel olarak konusursak enerji yogunluklari yaricapla ses hiziyla ters orantili olarak degisir dolayisiyla rezonans frekanslari agirlikli olarak Gunes in dis bolgeleri tarafindan belirlenir Sonuc olarak bunlardan gunes cekirdeginin yapisini cikarmak zordur Salinimlarin nerede g modu karakterine mavi sahip oldugunu veya dipol modlarinin nerede p modu karakterine turuncu sahip oldugunu gosteren standart bir gunes modeli icin yayilma diyagrami Kesikli cizgi daha hassas modellemeyle hesaplanan akustik kesme frekansini gosterir ve bu frekanslarin uzerinde modlarin yildizda sikisip kalmadigini ve kabaca konusursak yankilanmadigini gosterir Yercekimi modlari g modlari Yercekimi modlari isinimsal ic kisim veya atmosfer gibi konvektif olarak kararli bolgelerle sinirlidir Geri cagirici kuvvet agirlikli olarak kaldirma kuvvetidir ve dolayisiyla dolayli olarak yer cekimidir ki isimleri de buradan gelir Konveksiyon bolgesinde hizla kaybolurlar ve bu nedenle ic modlarin yuzeyde kucuk genlikleri vardir ve tespit edilmesi ve tanimlanmasi son derece zordur Sadece birkac g modunun olcumunun bile Gunes in derin ic kismina iliskin bilgimizi onemli olcude artirabilecegi uzun zamandir bilinmektedir Bununla birlikte dolayli tespitler hem iddia edilmis hem de bunlara karsi cikilmis olmasina ragmen hicbir bireysel g modu henuz kesin olarak olculmemistir Ayrica konvektif olarak kararli atmosferle sinirli benzer yercekimi modlari da olabilir Yuzey yercekimi modlari f modlari Yuzey yercekimi dalgalari derin sudaki dalgalara benzer ve Lagrangian basinc perturbasyonunun esasen sifir olmasi ozelligine sahiptir Yuksek derecedeki ℓ displaystyle ell karakteristik bir mesafeye nufuz ederek R ℓ displaystyle R ell olur ki burada R displaystyle R gunes yaricapidir Iyi bir yaklasimla derin su dalgasi dagilim yasasi olarak adlandirilan yasaya uyarlar w2 gkh displaystyle omega 2 gk rm h Gunes in katmanlasmasina bakilmaksizin w displaystyle omega acisal frekanstir g displaystyle g yuzey yercekimi ve kh ℓ R displaystyle k rm h ell R yatay dalga sayisidir ve bu iliskiye asimptotik kh displaystyle k rm h rightarrow infty olarak egilimlidir Sismoloji neyi ortaya cikarabilir Sismolojide basariyla kullanilan salinimlar esasen adyabatiktir Bu nedenle dinamikleri basinc kuvvetlerinin p displaystyle p arti varsayilan Maxwell gerilmeleri eylemsizlik yogunluguna r displaystyle rho sahip maddeye karsi etkisidir bu da adyabatik degisim altinda aralarindaki iliskiye baglidir ve genellikle birinci adyabatik us g1 displaystyle gamma 1 araciligiyla olculur p displaystyle p ve r displaystyle rho degiskenlerinin denge degerleri dinamik olarak kucuk acisal hiz W displaystyle Omega ve manyetik alanla B displaystyle rm B birlikte Gunes in toplam kutlesine M displaystyle M ve yaricapina R displaystyle R bagli olan hidrostatik destek kisitlamasiyla iliskilidir Acikcasi salinim frekanslari w displaystyle omega yalnizca sismik degiskenlere r p W B displaystyle rho p Omega rm B g1 displaystyle gamma 1 W displaystyle Omega ve B displaystyle rm B veya bunlarin herhangi bir bagimsiz fonksiyonuna baglidir Sonuc olarak bilginin dogrudan elde edilebilmesi yalnizca bu degiskenler ile ilgilidir Adyabatik ses hizinin karesi c2 g1p r displaystyle c 2 gamma 1 p rho yaygin olarak benimsenen bir fonksiyondur cunku akustik yayilimin esas olarak bagli oldugu miktar budur Helyum bollugu gibi sismik olmayan diger miktarlarin ozellikleriY displaystyle Y veya ana dizi yasit displaystyle t odot yalnizca ek varsayimlarla desteklenerek cikarim yapilabilir bu da sonucu daha belirsiz hale getirir Veri analiziKuresel helyosismoloji Cift logaritmik eksenler uzerinde Gunes ve Heliosferik Gozlemevi ndeki cihazlardan alinan veriler kullanilarak Gunes in guc spektrumu VIRGO SPM cihazinin uc gecis bandi neredeyse ayni guc spektrumunu gosterir GOLF un gorus hatti hiz gozlemleri granulasyon tarafindan uretilen kirmizi gurultuye karsi daha az duyarlidir Tum veri kumeleri 3 mHz civarindaki salinim modlarini acikca gostermektedir Gunes ve Heliosferik Gozlemevi ndeki GOLF ve VIRGO SPM cihazlarindan alinan veriler kullanilarak modlarin maksimum guce sahip oldugu Gunes in guc spektrumu Dusuk dereceli modlar l lt 4 duzenli araliklarla net bir tarak benzeri desen gosterir Orta acisal derecenin guc spektrumu 0 ℓ lt 300 displaystyle 0 leq ell lt 300 SOHO gemisindeki MDI cihazindan alinan 144 gunluk veriler uzerinden hesaplanan gunes salinimlari Renk skalasi logaritmiktir ve modlari daha gorunur kilmak icin sinyaldeki maksimum gucun yuzde birine doymustur Dusuk frekansli bolgeye granulasyon sinyali hakimdir Acisal derece arttikca bireysel mod frekanslari her biri bir dizi dusuk dereceli modlara karsilik gelen net sirtlar uzerinde birlesir Ham sismik verileri analiz etmenin baslica araci Fourier donusumudur Iyi bir yaklasimla her mod frekansin bir fonksiyonu olarak gucun bir Lorentz fonksiyonu oldugu sonumlu bir harmonik osilatordur Uzaysal olarak cozulmus veriler genellikle daha sonra Fourier donusumune tabi tutulan zaman serilerini elde etmek icin istenen kuresel harmoniklere yansitilir Helyosismologlar tipik olarak ortaya cikan tek boyutlu guc spektrumlarini iki boyutlu bir spektrumda birlestirirler Salinimlarin dusuk frekans araligi neden oldugu varyasyonlarin hakimiyetindedir Modlarin analiz edilmesinden once veya ayni zamanda bunun filtrelenmesi gerekir Gunes yuzeyindeki granuler akislar yukselen granullerin merkezlerinden aralarindaki dar asagi yonlu akimlara kadar cogunlukla yataydir Salinimlara bagli olarak granulasyon yogunluk acisindan gorus hatti hizindan daha guclu bir sinyal uretir bu nedenle ikincisi helyosismik gozlemevleri icin tercih edilir Yerel helyosismoloji Charles Lindsey Doug Braun ve Stuart Jefferies tarafindan 1993 te turetilen bir terim olan yerel helyosismoloji gozlemsel verilerden cikarimlar yapmak icin birkac farkli analiz yontemini kullanir Fourier Hankel spektral yontemi ilk olarak gunes lekelerinin dalga emilimini arastirmak icin kullanilmistir Ilk olarak Frank Hill tarafindan tanitilan halka diyagrami analizi gunes isinlarinin yamalari uzerinde hesaplanan gunes salinimlarinin guc spektrumlarindan ortamdaki akustik dalgalarin Doppler kaymalarini gozlemleyerek gunes yuzeyinin altindaki yatay akislarin hizini ve yonunu tipik olarak 15 15 cikarmak icin kullanilir Bu nedenle halka diyagrami analizi Gunes uzerindeki yerel alanlara Gunes in yarisinin aksine uygulanan kuresel helyosismolojinin bir genellemesidir Ornegin ses hizi ve adyabatik indeks manyetik olarak aktif ve aktif olmayan sessiz Gunes bolgelerde karsilastirilabilir Zaman mesafe heliosismolojisi gunes dalgalarinin gunes yuzeyindeki herhangi iki konum arasindaki seyahat surelerini olcmeyi ve yorumlamayi amaclamaktadir Iki konumu birbirine baglayan isin yolunun yakinindaki homojensizlikler bu iki nokta arasindaki seyahat suresini bozar Gunes ic kisminin yerel yapisini ve dinamiklerini anlamak icin ters bir problemin cozulmesi gerekir Uzak taraf manyetik goruntuleme amaciyla Charles Lindsey ve Doug Braun tarafindan ayrintili olarak tanitilan helyosismik holografi faza duyarli holografinin ozel bir durumudur Buradaki fikir Gunes in uzak tarafindaki aktif bolgeler hakkinda bilgi edinmek icin gorunur diskteki dalga alanini kullanmaktir Helyosismik holografideki temel fikir dalga alaninin ornegin gunes yuzeyinde gozlemlenen gorus hatti Doppler hizinin herhangi bir zamanda gunesin ic kismindaki herhangi bir konumdaki dalga alaninin tahminini yapmak icin kullanilabilmesidir Bu anlamda holografi jeofizikte 1940 lardan bu yana kullanilan bir teknik olan cok benzer Baska bir ornek olarak bu teknik bir gunes patlamasinin sismik goruntusunu vermek icin kullanilmistir Dogrudan modellemede amac Fourier alanindaki dalga alaninda gorulen frekans dalga sayisi korelasyonlarinin dogrudan ters cevrilmesinden yeralti akislarini tahmin etmektir Woodard teknigin yuzeye yakin akislari f modlarinda geri kazanma yetenegini gostermistir InversiyonGiris Gunes in salinim modlari onun surekli yapisina duyarli ayrik bir dizi gozlemi temsil eder Bu bilim adamlarinin Gunes in ic yapisi ve dinamigi icin formule etmelerine olanak tanir Gunes in bir referans modeli goz onune alindiginda mod frekanslari ile Gunes in mod frekanslari arasindaki farklar eger kucukse Gunes in yapisi ile referans modelin yapisi arasindaki farklarin agirlikli ortalamalaridir Frekans farkliliklari daha sonra bu yapisal farkliliklari anlamak icin kullanilabilir Bu ortalamalarin agirliklandirma fonksiyonlari cekirdekler olarak bilinir Yapi Gunes in yapisinin ilk ters cevrilmeleri Duvall yasasi kullanilarak yapilmisti ve daha sonra bir referans gunes modeli etrafinda dogrusallastirilan Duvall yasasi kullanilarak yapildi Bu sonuclar daha sonra teorik bir referans modeli hakkindaki yildiz salinimlarini tanimlayan denklemlerin tam setini dogrusallastiran analizlerle desteklenmistir ve artik frekans verilerini tersine cevirmenin standart bir yolu haline gelmistir Ters cevirmeler gunes modellerindeki farkliliklari gosterir bunlar yercekimsel cokelmenin uygulanmasiyla buyuk olcude azaltilmistir daha agir elementlerin gunes merkezine dogru kademeli olarak ayrilmasi ve bunlarin yerini almak uzere daha hafif elementlerin yuzeye cikmasi Dondurme Gunes in ic donus profili Gunes Dinamikleri Gozlemevi ndeki Helyoseismik ve Manyetik Goruntuleyiciden alinan veriler kullanilarak cikarildi Olcumlerin 1 den daha az kesin oldugu durumlarda ic yaricap kesilmistir bu cekirdege giden yolun yaklasik 3 4 unde gerceklesir Kesikli cizgi takoklin olarak bilinen donus profilinin degistigi sinirla cakisan gunes konveksiyon bolgesinin tabanini gosterir Eger Gunes tamamen kuresel olsaydi farkli azimut dereceleri m olan modlar ayni frekanslara sahip olurdu Ancak donus bu bozulmayi kirar ve modlarin frekanslari Gunes teki acisal hizin agirlikli ortalamalari olan donussel bolunmelerle farklilik gosterir Farkli modlar Gunes in farkli bolgelerine duyarlidir ve yeterli veri verildiginde bu farklar Gunes boyunca donus hizini anlamak icin kullanilabilir Ornegin Gunes her yerinde duzgun bir sekilde donuyor olsaydi tum p modlari yaklasik olarak ayni miktarda bolunurdu Aslinda ekvatorun kutuplardan daha hizli dondugu yuzeyde goruldugu gibi acisal hiz duzgun degildir Gunes kuresel donmeyen bir modelin donen cekirdeklerin turetilmesi icin gercege yeterince yakin olmasini saglayacak kadar yavas doner Helyoseismoloji Gunes in cesitli ozelliklere sahip bir donme profiline sahip oldugunu gostermistir ic cekirdegin donus hizi iyi bilinmemekle birlikte kati sekilde donen isinimli yani konvektif olmayan bir bolge rijit bir sekilde donen ic kisim ile diferansiyel olarak donen konvektif kabugu ayiran takoklin olarak bilinen ince bir kesme katmani donus hizinin hem derinlige hem de enleme gore degistigi konvektif bir zarf ve Yuzeyin hemen altinda donme hizinin yuzeye dogru yavasladigi son kayma tabakasi Diger alanlarla iliskiJeosismoloji Helyosismoloji jeosismoloji ile benzerlikten dogmustur ancak bazi onemli farkliliklar devam etmektedir Birincisi Gunes in kati bir yuzeyi yoktur ve bu nedenle kayma dalgalarini destekleyemez Veri analizi perspektifinden bakildiginda kuresel helyosismoloji yalnizca normal modlari incelemesi nedeniyle jeosismolojiden farklilik gosterir Dolayisiyla yerel helyosismoloji dalga alaninin tamamini incelemesi anlaminda jeosismolojiye ruhen biraz daha yakindir Asterosismoloji Gunes bir yildiz oldugu icin helyosismoloji asterosismoloji olarak bilinen diger yildizlardaki salinimlarin incelenmesiyle yakindan ilgilidir Helyoseismoloji salinimlari ayni zamanda olarak bilinen dis konveksiyon bolgeleri tarafindan yonlendirilen ve sonumlenen yildizlarin incelenmesiyle en yakindan iliskilidir ancak temeldeki teori diger degisken yildiz siniflari icin genel olarak aynidir Temel fark uzak yildizlardaki salinimlarin cozulememesidir Kuresel harmonigin daha parlak ve daha karanlik sektorleri iptal edildiginden bu durum asterosismolojiyi neredeyse tamamen dusuk dereceli modlarin acisal derece ℓ 3 displaystyle ell leq 3 incelenmesiyle sinirlandirir Bu ters cevirmeyi cok daha zorlastirir ancak daha kisitlayici varsayimlar yapilarak ust sinirlara yine de ulasilabilir TarihGunes salinimlari ilk olarak 1960 larin basinda yaklasik 5 dakikalik bir periyotla yari periyodik yogunluk ve gorus hatti hiz degisimi olarak gozlemlenmistir Bilim adamlari yavas yavas salinimlarin Gunes in kuresel modlari olabilecegini fark ettikten sonra modlarin iki boyutlu guc spektrumunda net sirtlar olusturacagi ongoruldu Sirtlarin olustugu daha sonra 1970 lerin ortalarinda yuksek dereceli modlarin gozlemleri sirasinda dogrulandi ve farkli radyal duzenlerin mod coklulari tam disk gozlemlerinde ayirt edilebildi Hemen hemen ayni tarihlerde ve Douglas Gough Gunes in ic yapisini anlamak icin bireysel mod frekanslarini kullanma potansiyelini one surduler Gunes modellerini dusuk dereceli verilere gore kalibre ederek biri dusuk Y displaystyle Y ve buna karsilik gelen dusuk notrino uretim hizina sahip Ln displaystyle L nu digeri daha yuksek Y displaystyle Y ve Ln displaystyle L nu ye sahip iki benzer iyi uyum bularak kalibre ettiler yuksek dereceli frekanslara karsi daha onceki zarf kalibrasyonlari ikincisini tercih ediyordu ancak sonuclar tamamen ikna edici degildi Ta ki Tom Duvall ve Jack Harvey daha onceki gozlemlerle iliskili kuantum sayilarini olusturmak icin orta dereceden modlari olcerek iki ekstrem veri setini birbirine baglayana kadar daha yuksek Y displaystyle Y model olusturuldu ve boylece bu erken asamada notrino probleminin cozumunun nukleer veya parcacik fiziginde olmasi gerektigi one suruldu 1980 lerde gelistirilen yeni ters cevirme yontemleri arastirmacilarin Gunes in buyuk bolumunde ses hizi ve daha az dogru bir sekilde yogunluk profilleri hakkinda cikarim yapmasina olanak taniyarak notrino sorununun nedeninin gunes yapisi cikarimindaki kalici hatalarin olmadigi sonucunu dogruluyor On yilin sonuna dogru gozlemler salinim modu frekanslarinin Gunes in manyetik aktivite dongusune gore degistigini de gostermeye baslamistir Geceleri Gunes i gozlemleyememe sorununun ustesinden gelmek icin birkac grup ornegin kisaca BiSON ve Gunes in her zaman en az bir dugum tarafindan gorulebilecegi teleskop aglari kurmaya baslamisti Uzun kesintisiz gozlemler alani olgunluga eristirdi ve alanin durumu Science dergisinin 1996 yilindaki ozel sayisinda ozetlendi Bu helyosismoloji icin yuksek kaliteli veriler uretmeye baslayan Gunes ve Heliosferik Gozlemevi nin SoHO normal operasyonlarinin baslamasiyla ayni zamana denk gelmisti Sonraki yillarda gunes notrinosu sorununun cozuldugu goruldu ve uzun sismik gozlemler birden fazla gunes aktivite dongusunun analizine izin vermeye basladi Standart gunes modelleri ile helyosismik inversiyonlar arasindaki uyum ayrintili uc boyutlu modellere dayali olarak gunes fotosferindeki agir element iceriginin yeni olcumleriyle bozuldu Her ne kadar sonuclar daha sonra 1990 larda kullanilan geleneksel degerlere dogru kaymis olsa da yeni bolluklar modeller ile helyosismik inversiyonlar arasindaki uyumu onemli olcude kotulestirdi Tutarsizligin nedeni cozulememisti ve gunes bollugu problemi olarak bilinmektedir SoHO nun uzay tabanli gozlemleri devam etti ve 2010 yilinda SoHO ya faaliyetlerine basladigi gunden bu yana Gunes i surekli olarak izleyen Gunes Dinamikleri Gozlemevi SDO de katildi Ek olarak yer tabanli aglar ozellikle BiSON ve GONG calismaya devam ederek yerden de neredeyse surekli veri saglamaktadir Ayrica bakinizYigilma diski Solar notrino problemiKaynakca Gough D O Kosovichev A G Toomre J ve digerleri 1996 The seismic structure of the Sun Science 272 5266 ss 1296 1300 doi 10 1126 science 272 5266 1296 PMID 8662458 a b Gizon L Birch A C 2005 Local Helioseismology Living Reviews in Solar Physics 2 1 s 6 doi 10 12942 lrsp 2005 6 Fukuda Y Super Kamiokande Collaboration 1998 Evidence for oscillation of atmospheric neutrinos Phys Rev Lett 81 8 ss 1562 1567 arXiv hep ex 9807003 2 doi 10 1103 PhysRevLett 81 1562 Bahcall J N Concha Gonzalez Garcia M Pe na Garay C 2001 Global analysis of solar neutrino oscillations including SNO CC measurement Journal of High Energy Physics 2001 8 s 014 arXiv hep ph 0106258 2 doi 10 1088 1126 6708 2001 08 014 Bahcall J N 2001 High energy physics Neutrinos reveal split personalities Nature 412 6842 ss 29 31 doi 10 1038 35083665 PMID 11452285 Webb Jonathan 6 Ekim 2015 Neutrino flip wins physics Nobel Prize BBC News 15 Nisan 2022 tarihinde kaynagindan Erisim tarihi 28 Eylul 2023 Duvall T L Jr Dziembowski W A Goode P R Gough D O Harvey J W Leibacher J W 1984 The internal rotation of the Sun Nature 310 5972 ss 22 25 doi 10 1038 310022a0 Pijpers F P 1998 Helioseismic determination of the solar gravitational quadrupole moment Mon Not R Astron Soc 297 3 ss L76 L80 arXiv astro ph 9804258 2 doi 10 1046 j 1365 8711 1998 01801 x Antia H M Chitre S M Gough D O 2008 Temporal variations in the Sun s rotational kinetic energy Astron Astrophys 477 2 ss 657 663 arXiv 0711 0799 2 doi 10 1051 0004 6361 20078209 Spiegel E A Zahn J P 1992 The solar tachocline Astronomy and Astrophysics 265 s 106 Fan Y 2009 Magnetic Fields in the Solar Convection Zone Living Reviews in Solar Physics 6 1 s 4 doi 10 12942 lrsp 2009 4 Gough D O McIntyre M E 1998 Inevitability of a magnetic field in the Sun s interior Nature 394 6695 s 755 doi 10 1038 29472 a b Grec G Fossat E Pomerantz M 1980 Solar oscillations full disk observations from the geographic South Pole Nature 288 5791 ss 541 544 doi 10 1038 288541a0 a b Duvall Jr T L Harvey J W 1983 Observations of solar oscillations of low and intermediate degree Nature 302 5903 s 24 doi 10 1038 302024a0 Christensen Dalsgaard J Dappen W Ajukov S V Anderson E R Antia H M Basu S Baturin V A Berthomieu G Chaboyer B Chitre S M 1996 The Current State of Solar Modeling Science 272 5266 ss 1286 92 doi 10 1126 science 272 5266 1286 PMID 8662456 Christensen Dalsgaard J Dappen W Ajukov S V and 1996 The Current State of Solar Modeling Science 272 5266 ss 1286 1292 doi 10 1126 science 272 5266 1286 PMID 8662456 Appourchaux T Belkacem K Broomhall A M Chaplin W J Gough D O Houdek G Provost J Baudin F Boumier P Elsworth Y 2010 The quest for the solar g modes Astronomy and Astrophysics Review 18 1 2 s 197 arXiv 0910 0848 2 doi 10 1007 s00159 009 0027 z a b Gough D O 1984 Solar inverse theory Solar Seismology from Space Ed R K Ulrich JPL Publ Pasadena 84 84 ss 49 78 Garc ia R A Turck Chi eze S Jimenez Reyes S J Ballot J Palle P L Eff Darwich A Mathur S Provost J 2007 Tracking Solar Gravity Modes The Dynamics of the Solar Core Science 316 5831 ss 1591 3 doi 10 1126 science 1140598 PMID 17478682 Fossat E Boumier P Corbard T Provost J Salabert D Schmider F X Gabriel A H Grec G Renaud C Robillot J M 2017 Asymptotic g modes Evidence for a rapid rotation of the solar core Astronomy and Astrophysics 604 ss A40 arXiv 1708 00259 2 doi 10 1051 0004 6361 201730460 Schunker H Schou J Gaulme P Gizon L 2018 Fragile Detection of Solar g Modes by Fossat et al Solar Physics 293 6 s 95 arXiv 1804 04407 2 doi 10 1007 s11207 018 1313 6 Scherrer P H Gough D O 2019 A critical evaluation of recent claims concerning solar rotation Astrophysical Journal 877 1 ss 42 53 arXiv 1904 02820 2 doi 10 3847 1538 4357 ab13ad Gough D O 1982 A review of the theory of solar oscillations and its implications concerning the internal structure of the Sun In Pulsations in Classical and Cataclysmic Variable Stars Ed J P Cox amp C J Hansen JILA Boulder ss 117 137 Gough D O 2003 What have we learned from helioseismology what have we really learned and what do we aspire to learn Solar Physics 287 1 2 ss 9 41 arXiv 1210 0820 2 doi 10 1007 s11207 012 0099 1 Kosovichev A G Christensen Dalsgaard J Daeppen W Dziembowski W A Gough D O Thompson M J 1992 Sources of uncertainty in direct seismological measurements of the solar helium abundance Mon Not R Astron Soc 259 3 ss 536 558 Bibcode 1992MNRAS 259 536K doi 10 1093 mnras 259 3 536 Houdek G Gough D O 2011 On the seismic age and heavy element abundance of the Sun Mon Not R Astron Soc 418 2 ss 1217 1230 arXiv 1108 0802 2 Bibcode 2011MNRAS 418 1217H doi 10 1111 j 1365 2966 2011 19572 x Rhodes Jr E J Kosovichev A G Schou J ve digerleri 1997 Measurements of Frequencies of Solar Oscillations from the MDI Medium l Program Solar Physics 175 2 s 287 doi 10 1023 A 1004963425123 Lindsey C Braun D C Jefferies S M Ocak 1993 T M Brown Ed Local Helioseismology of Subsurface Structure in GONG 1992 Seismic Investigation of the Sun and Stars GONG 1992 Seismic Investigation of the Sun and Stars Proceedings of a Conference Held in Boulder Astronomical Society of the Pacific Conference Series 42 ss 81 84 ISBN 978 0 937707 61 6 Braun D C Duvall Jr T L Labonte B J Agustos 1987 Acoustic absorption by sunspots The Astrophysical Journal 319 L27 L31 doi 10 1086 184949 Hill F Ekim 1988 Rings and trumpets Three dimensional power spectra of solar oscillations Astrophysical Journal 333 996 1013 doi 10 1086 166807 Basu S Antia H M Bogart R S Agustos 2004 Ring Diagram Analysis of the Structure of Solar Active Regions The Astrophysical Journal 610 2 1157 1168 doi 10 1086 421843 Duvall Jr T L Jefferies S M Harvey J W Pomerantz M A Nisan 1993 Time distance helioseismology Nature 362 6419 430 432 doi 10 1038 362430a0 Jensen J M 2003 Time distance what does it tell us Gong 2002 Local and Global Helioseismology The Present and Future 517 s 61 Braun D C Lindsey C 2001 Seismic Imaging of the Far Hemisphere of the Sun Astrophysical Journal Letters 560 2 ss L189 doi 10 1086 324323 Donea A C Braun D C Lindsey C Mart 1999 Seismic Images of a Solar Flare The Astrophysical Journal 513 2 L143 L146 doi 10 1086 311915 Woodard M F Ocak 2002 Solar Subsurface Flow Inferred Directly from Frequency Wavenumber Correlations in the Seismic Velocity Field The Astrophysical Journal 565 1 634 639 doi 10 1086 324546 Christensen Dalsgaard J Duvall Jr T L Gough D O Harvey J W Rhodes Jr E J 1985 Speed of sound in the solar interior Nature 315 6018 s 378 doi 10 1038 315378a0 Christensen Dalsgaard J Thompson M J Gough D O 1989 Differential asymptotic sound speed inversions MNRAS 238 2 ss 481 502 doi 10 1093 mnras 238 2 481 Dziembowski W A Pamyatnykh A A Sienkiewicz R 1990 Solar model from helioseismology and the neutrino flux problem Mon Not R Astron Soc 244 ss 542 550 Antia H M Basu S 1994 Nonasymptotic helioseismic inversion for solar structure Astronomy amp Astrophysics Supplement Series 107 s 421 Gough D O Thompson M J 1991 The inversion problem M S Matthews W C Livingston Ed Solar interior and atmosphere Tucson University of Arizona Press ss 519 561 Basu S 2016 Global seismology of the Sun Living Reviews in Solar Physics 13 1 s 2 arXiv 1606 07071 2 doi 10 1007 s41116 016 0003 4 Cox A N Guzik J A Kidman R B 1989 Oscillations of solar models with internal element diffusion Astrophysical Journal 342 s 1187 doi 10 1086 167675 28 Eylul 2023 tarihinde kaynagindan erisim tarihi 28 Eylul 2023 Christensen Dalsgaard J Proffitt C R Thompson M J 1993 Effects of diffusion on solar models and their oscillation frequencies PDF Astrophysical Journal Letters 403 ss L75 doi 10 1086 186725 23 Mart 2022 tarihinde kaynagindan PDF erisim tarihi 28 Eylul 2023 Thompson M J Christensen Dalsgaard J Miesch M S Toomre J 2003 The Internal Rotation of the Sun Annual Review of Astronomy amp Astrophysics 41 ss 599 643 doi 10 1146 annurev astro 41 011802 094848 Beck J G 2000 A comparison of differential rotation measurements Invited Review Solar Physics 191 1 ss 47 70 doi 10 1023 A 1005226402796 Howe R 2009 Solar Interior Rotation and its Variation Living Reviews in Solar Physics 6 1 s 1 arXiv 0902 2406 2 doi 10 12942 lrsp 2009 1 Leighton R B Noyes R W Simon G W 1962 Velocity Fields in the Solar Atmosphere I Preliminary Report Astrophysical Journal 135 s 474 doi 10 1086 147285 Evans J W Michard R 1962 Observational Study of Macroscopic Inhomogeneities in the Solar Atmosphere III Vertical Oscillatory Motions in the Solar Photosphere Astrophysical Journal 136 s 493 doi 10 1086 147403 Leibacher J W Stein R F 1971 A New Description of the Solar Five Minute Oscillation Astrophysical Letters 7 s 191 Ulrich R K 1970 The Five Minute Oscillations on the Solar Surface Astrophysical Journal 162 s 993 doi 10 1086 150731 Deubner F L 1975 Observations of low wavenumber nonradial eigenmodes of the sun Astronomy and Astrophysics 44 2 s 371 Rhodes Jr E J Ulrich R K Simon G W 1977 Observations of nonradial p mode oscillations on the sun Astrophysical Journal 218 s 901 doi 10 1086 155745 Claverie A Isaak G R McLeod C P van der Raay H B Cortes T R 1979 Solar structure from global studies of the 5 minute oscillation Nature 282 5739 ss 591 594 doi 10 1038 282591a0 Christensen Dalsgaard J Gough D O 1976 Towards a heliological inverse problem Nature 259 5539 s 89 doi 10 1038 259089a0 Christensen Dalsgaard J Gough D O 1981 Comparison of the observed solar whole disk oscillation frequencies with the predictions of a sequence of solar models Astron Astrophys 104 2 ss 173 176 Gough D O 1977 Random remarks on solar hydrodynamics Proc IAU Colloq 36 ss 3 36 Rhodes Jr E J Ulrich R K 1977 The sensitivity of nonradial p mode eigenfrequencies to solar envelope structure Astrophysical Journal 218 ss 521 529 doi 10 1086 155705 Libbrecht K G Woodard M F 1990 Solar cycle effects on solar oscillation frequencies Nature 345 6278 s 779 doi 10 1038 345779a0 Aindow A Elsworth Y P Isaak G R McLeod C P New R Vanderraay H B 1988 The current status of the Birmingham solar seismology network Seismology of the Sun and Sun Like Stars 286 s 157 Chaplin W J Elsworth Y Howe R Isaak G R McLeod C P Miller B A van der Raay H B Wheeler S J New R 1996 BiSON Performance Solar Physics 168 1 s 1 doi 10 1007 BF00145821 Harvey J W Hill F Kennedy J R Leibacher J W Livingston W C 1988 The Global Oscillation Network Group GONG Advances in Space Research 8 11 s 117 doi 10 1016 0273 1177 88 90304 3 Special Issue GONG Helioseismology Science 272 5266 1996 20 Agustos 2023 tarihinde kaynagindan erisim tarihi 28 Eylul 2023 Chaplin W J Elsworth Y Miller B A Verner G A New R 2007 Solar p Mode Frequencies over Three Solar Cycles Astrophysical Journal 659 2 s 1749 doi 10 1086 512543 Bahcall J N Pinsonneault M H Basu S 2001 Solar Models Current Epoch and Time Dependences Neutrinos and Helioseismological Properties Astrophysical Journal 555 2 ss 990 1012 arXiv astro ph 0010346 2 doi 10 1086 321493 Asplund M Grevesse N Sauval A J 2005 The Solar Chemical Composition Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis 336 s 25 Asplund M Grevesse N Sauval A J Scott P 2009 The Chemical Composition of the Sun Annual Review of Astronomy amp Astrophysics 47 1 ss 481 522 arXiv 0909 0948 2 doi 10 1146 annurev astro 46 060407 145222 Bahcall J N Basu S Pinsonneault M Serenelli A M 2005 Helioseismological Implications of Recent Solar Abundance Determinations Astrophysical Journal 618 2 ss 1049 1056 arXiv astro ph 0407060 2 doi 10 1086 426070 Gough D O 2003 What have we learned from helioseismology what have we really learned and what do we aspire to learn Solar Physics 287 1 2 ss 9 41 arXiv 1210 0820 2 doi 10 1007 s11207 012 0099 1 Dis baglantilarKasim 2009 da alindi Gough D O 2003 Solar Neutrino Production Annales Henri Poincare 4 S1 303 317 Bibcode 2003AnHP 4 303G doi 10 1007 s00023 003 0924 z Gizon Laurent Birch Aaron C 2005 Local Helioseismology Living Rev Sol Phys 2 1 6 Bibcode 2005LRSP 2 6G doi 10 12942 lrsp 2005 6 Bilim Adamlari Bir Sonraki Gunes Lekesi Dongusuyle Ilgili Benzeri Gorulmemis Tahminler Yayinladi Ulusal Bilim Vakfi basin aciklamasi 6 Mart 2006 Miesch Mark S 2005 Large Scale Dynamics of the Convection Zone and Tachocline Living Rev Sol Phys 2 1 1 Bibcode 2005LRSP 2 1M doi 10 12942 lrsp 2005 1 Gunes in Uzak Taraf ve Dunya Tarafi goruntuleri Gunes Fiziginde Yasayan Incelemeler MPS de Helyosismoloji ve AsterosismolojiUydu araclari VIRGO SOI MDI SDO HMIYer bazli aletler BISON Mark 1 GONG HiDHNDaha fazla okumaChristensen Dalsgaard Jorgen 21 Subat 2003 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Haziran 2015 Pijpers Frank P 2006 Methods in Helio and Asteroseismology Londra Imperial College Press ISBN 978 1 8609 4755 1
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

